基于比例风险模型的飞机部件剩余寿命预测

何 浪，鲁 亮+，陆锦鹤，范圣娴，赵立新，张宇翔

(1.中国民航大学 计算机科学与技术学院，天津 300300；(2.北京飞机维修工程有限公司 附件/起落架大修产品事业部，北京 100621)

0 引 言

全球的空中交通运输量正在快速增加，预计到2037年民航客机总数将达到45 265架[1]。在商业运营中，民用飞机的维修成本通常占航空公司直接运营成本的10%～20%[2]，准确预测飞机部件从当前状态到失效状态的剩余寿命可以提早预警飞机部件故障，并合理制定维修计划，从而有效降低维修成本，这在航空公司的安全运行和成本控制方面至关重要。

在现有工业设备的剩余寿命预测方法中[3，4]，基于数据驱动的方法不依赖设备的失效原理，而是通过对设备运行数据进行建模分析来预测设备剩余寿命，因而被广泛使用。该方法可大致分为基于退化数据的方法和基于失效数据的方法两类[5]。前者虽然可以通过多传感器信息提高剩余寿命预测的精度[6-8]，但是增加了系统的复杂性及成本[9]；而后者则需选择合适的寿命分布，且需要足够的失效数据进行分布拟合。文献[10，11]分别解决了寿命分布的选择问题和分布拟合的数据量问题，但没有考虑飞机各部件寿命的个体差异。事实上，一些飞机部件在进行拆换时会从备件仓库中选出调试好的部件进行更换，这些部件可能经历了不同的飞行时长、维修模式以及维修次数等。此外，文献[12]中指出，飞机年龄、飞机发动机型号等飞机参数也可能成为影响飞机故障概率的潜在因素。若将这些因素与部件的失效数据结合，可进一步提高寿命预测结果的精确度，并使其具有良好的可解释性。

比例风险模型(proportional hazard model，PHM)[13]作为一种可以分析多个变量与生存时间之间关系的统计回归模型，能处理可靠性数据且不需要提前对生存分布进行假设，正逐渐被应用于可靠性领域[14，15]与航空发动机的剩余寿命预测研究中。文献[16-18]基于该模型分析了多个参数对飞机发动机、辅助动力装置(auxiliary power unit，APU)等部件寿命的影响，但仍利用部件的状态监测数据进行寿命预测，忽略了部件状态以及部件所处环境对其寿命的影响。此外，飞机由大量的子系统和部件组成，很难直接获取到部分部件可用的状态监测数据。

本文弥补了基于失效数据方法在考虑部件个体差异时存在的不足，同时规避了基于状态监测数据的方法存在的问题，综合运用飞机部件的历史维修数据和历史失效数据，提出了一种基于比例风险模型的飞机部件剩余寿命预测方法，并通过对比实验验证其有效性。

1 飞机部件剩余寿命预测

1.1 可靠性分析

可靠性分析是剩余寿命预测的基础[19]。可靠性是指部件在规定条件和规定时间间隔内执行指定功能的能力，涉及失效概率F、可靠度R和失效率h等统计指标。

设寿命T为部件从完好状态到失效状态所经历的时间，失效(故障)概率F表示部件工作时间T小于t时失效的概率，可表示为

(1)

其中，f(x) 表示T的概率密度函数。在工程实践中，该变量通常通过实验评估确定。

可靠度R指设备工作时间T大于t的概率，可用式(2)表示

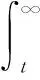
(2)

失效率h描述为设备工作时间到t，并在时刻t后单位时间内失效的概率

(3)

由式(2)可知f(x)=-dR(t)/dt， 代入式(3)中，则有

(4)

对等式(4)左右两边同时积分可推出可靠度R与失效率h之间的关系

(5)

1.2 比例风险模型

比例风险模型的基本形式定义为

h(t|X)=h0(t)exp(βX)

(6)

其中，h0(t) 表示各特征变量均为0时的基本失效率函数，h(t|X) 表示各特征变量的值均固定时的失效率函数，X=(X1，X2，…，Xp)T为影响部件剩余寿命的特征向量，β=(β1，β2，…，βp) 为相关特征对应的系数向量，表示特征变量对部件寿命的影响程度，p表示特征的个数。

1.2.1 特征选择

为了保留每个特征的实际意义并避免由自变量之间存在的相关关系，即多重共线性造成的特征冗余，采用逐步回归法对主要特征进行筛选。逐步回归法根据检验的显著性对特征变量逐个分析，通过与设定的显著性水平对比，以此来决定对该特征变量进行引入或者剔除。其步骤如下：

(1)对于未引入的特征变量，从中选择与因变量相关程度最高的特征变量并建立回归方程，进行显著性检验。若通过检验，则重复该步骤；否则转步骤(2)。

(2)对于已引入的特征变量，进行显著性检验，若检验不通过，则剔除该特征变量，确保每次引入新的特征变量之前回归方程只包含显著的变量，转步骤(1)；否则结束。

此外，在引入特征变量的过程中，其先后顺序并不代表其在最终回归方程中的重要程度，后引入的相对重要的特征变量则会因为多重共线性而被剔除。因此，需要在进行逐步回归前进行多重共线性的诊断。

多重共线性的诊断方法主要分为两类，一类是经验式的诊断方法，包括观察特征变量的相关系数矩阵、通过专业知识或一般经验分析回归系数的代数符号以及某一个特征变量是另一部特征变量的近似线性组合等。另一类为统计诊断方法，其最主要的方法为使用方差膨胀因子。特征变量Xp的方差膨胀因子记为VIFp，公式如下

(7)

1.2.2 比例风险模型假定的检验

比例风险模型要求各特征变量的作用效应不随时间的变化而变化，故在建立比例风险模型前需要进行比例风险假设验证。现有比例风险假设方法可分为图示法和假设检验法，其中图示法具有清晰、实用等特点，主要包括Cox &K-M比较法[13]、累积风险函数图示法[20]以及Schoenfeld残差法[21]。

Cox &K-M比较法最早由Cox提出，通过将比例风险模型和Kaplan-Meier估计的各组生存曲线进行比较，若曲线的趋势一致且无交叉，则满足比例风险假定。

累积风险函数图示法可通过观察对数累积风险函数对时间的趋势图，若各组曲线互相平行，则满足比例风险假定。

根据式(6)以及累积风险函数可知

(8)

对等式(8)两边取对数

lnH(t|X)=lnH0(t)+βX

(9)

由上式可知，若不同组间的对数累积风险函数差值lnH(t|X1)-lnH(t|X2)=β(X1-X2) 为常数，则对应图像中各组曲线应保持平行或重叠。

Schoenfeld残差法最早由Schoenfeld提出，在ti时刻部件的偏残差ri定义如下

ri=(ri1，ri2，…，rik)

(10)

(11)

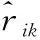
1.2.3 参数估计

由式(6)可知，比例风险模型可以看作基本失效率函数的非参数部分和一个与失效因素线性相关的参数部分的乘积。

对于非参数部分，不同部件的生存时间对应的分布不同。常见的寿命分布函数有正态分布、指数分布、威布尔分布、对数正态分布、伽马分布等，需选择最适合部件的分布函数对其生存时间分布进行拟合。首先通过极大似然估计得到相应分布的参数，然后根据AD检验统计量的大小选择合适的分布类型。

对于参数部分，协变量的参数估计通常可以用以下偏似然方程进行求解

(12)

其中，n表示观测样本的数量，δi为状态变量。当δi=0时表示部件在故障前被拆除，δi=1时则表示部件故障时被拆除。

式(12)的对数方程为

(13)

lnL(β) 的一阶导数为

(14)

根据式(13)和式(14)，可采用梯度下降法对参数进行估计。另一种办法则是继续求出式(13)的二阶偏导，然后利用Newton-Raphson方法进行参数估计。该方法虽然收敛快，但是需要计算二阶偏导以及矩阵的逆，计算复杂度偏大。

1.3 剩余寿命预测

在获得参数β的估计值后，将式(6)代入式(5)中可以推出在X条件下的可靠度函数

(15)

对等式(15)两边取对数

(16)

剩余寿命的平均值为

(17)

根据式(16)、式(17)可得到t时刻在X条件下的平均剩余寿命

(18)

本文采取固定时间点预测的方式预测部件的剩余寿命。如图1所示，根据部件的平均更换间隔时间设置预测点t1，t2，…，tn， 在各预测点对飞机轮胎进行剩余寿命的预测。

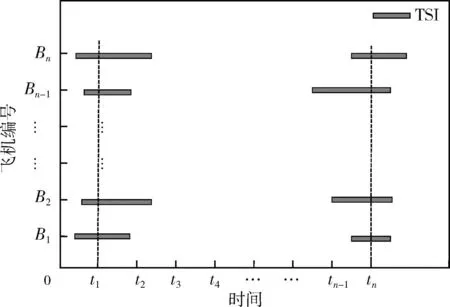
图1 预测间隔

2 数据集描述

本文使用的数据集收集自北京飞机维修工程有限公司。数据集包含858个部件，共85 259条维修记录，涉及163架B737 NG型号的飞机，其时间跨度为2016-2019年。数据属性包括收货日期、部件编号、维修模式代码、维修费用、装机日期、拆卸日期、部件自出厂到现在的累计飞行小时数(time since new，TSN)、部件自上次大修以来的累计飞行小时数(time since overhaul，TSO)、部件本次装机到拆卸之间的累计飞行小时数(time since install，TSI)，部件本次装机到拆卸之间的累计飞行小时数、飞机编号、发动机型号、飞机制造日期等。其中，TSI为因变量，表示部件的寿命。根据数据的可用性以及部件的经济效益，在本文实验中选择主轮的装拆记录进行数据分析，并从部件自身以及部件所处环境两个方面进行特征提取。对于主轮自身，TSN、TSO、部件累计维修次数(TIMES)以及维修的模式(MODE)都可能会影响部件的寿命。飞机在减速刹车时，主轮要面临急剧的温度变化，可能对轮胎的寿命造成影响，因此可以考虑环境温度变化的影响，故将季度(Quarter)作为主轮的备选特征。此外，考虑飞机的结构的老化以及发动机推力的不同，也有可能影响主轮的寿命，故将主轮所在飞机的年龄(AGE)和发动机型号(Engine)作为备选特征。表1给出了主轮备选特征描述。

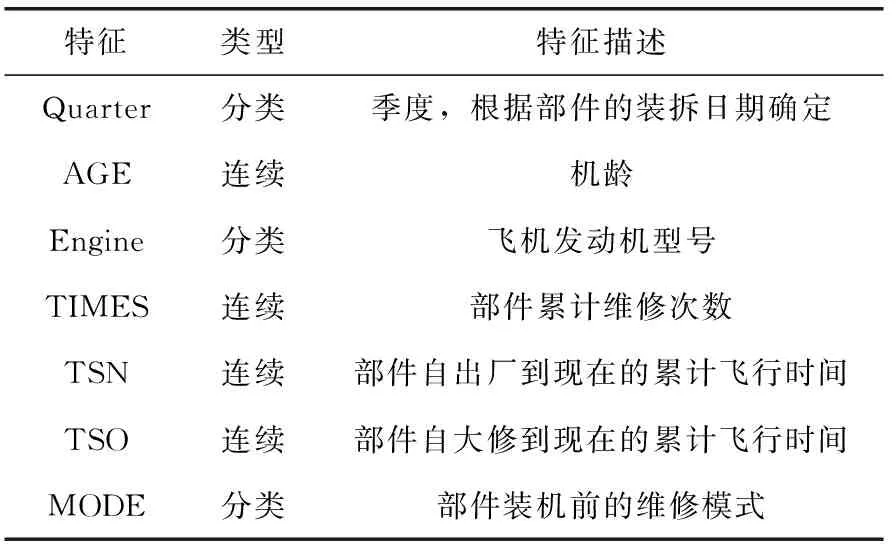
表1 特征描述

表2中为各连续型变量的描述性统计。为了更好地评估这些参数对TSI的影响，需要对这些连续变量进行归一化。归一化方法如下

表2 连续变量的描述性统计

(19)

其中，Z1max、Z1min、Z2max、Z2min、Z3max、Z3min、Z4max和Z4min分别表示TSN、TSO、AGE以及TIMES的最大最小值。

对于分类变量，采用箱形图展示各分类变量关于TSI的数据分布，如图2所示。

图2 分类变量的数据分布

在图2(a)中，维修模式包括新件(NEW)、修理(repair，RP)和大修(overhaul，OH)。

3 模型验证与分析

3.1 主轮与TSI分布分析

通过常见寿命分布函数对主轮的TSI进行拟合，然后根据AD检验统计量选用AD值较小的分布函数。表3中给出了拟合效果较好的分布的参数估计结果。

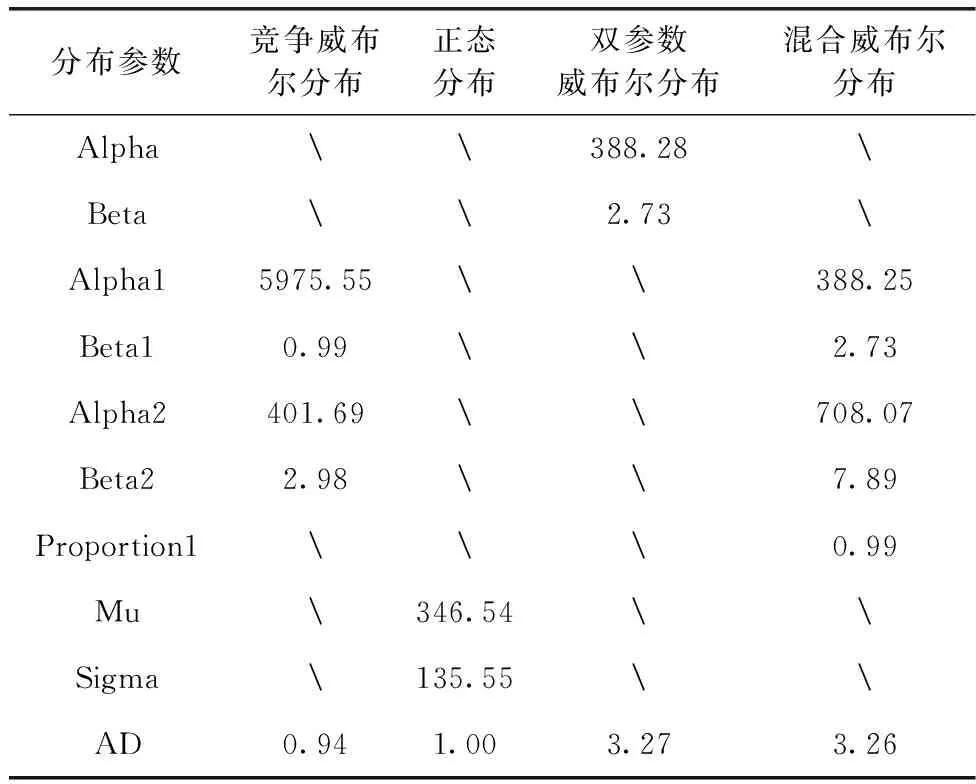
表3 各分布参数估计结果

图3为各分布的拟合结果，图中的直方图为主轮TSI的数据分布。从图中可以看出这几种分布曲线与主轮的数据分布都较为接近，拟合的效果较好。

图3 分布曲线拟合

3.2 检验与回归结果

在逐步回归筛选的过程中，TIMES与MODE被剔除。其中，TIMES与TSN存在多重共线性，而MODE的显著性检验未通过。通过逐步回归筛选后，TSN、TSO、AGE、Engine和Quarter是筛选出的对TSI影响最显著的特征变量。

对主轮进行比例风险回归建模之前，需要对所选特征变量进行比例风险假设验证。选择基于累积风险函数图示法和Schoenfeld残差法分别对分类变量和连续变量进行比例风险假设验证。由图4可以看出发动机型号、季度等分类变量的对数累积风险函数关于TSI的曲线都基本平行或等距，说明这几个参数满足比例风险假定。

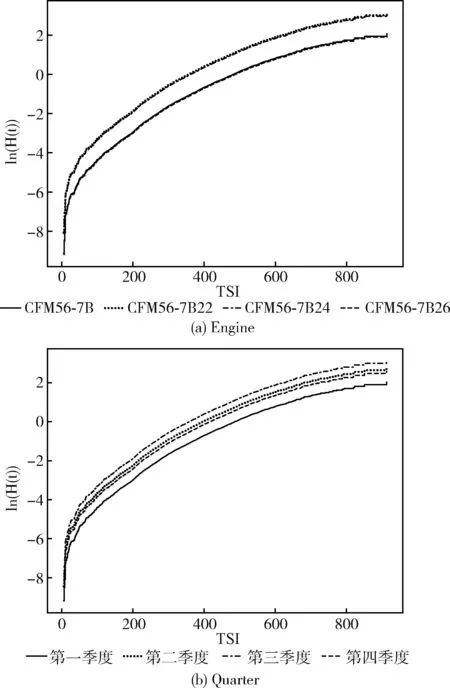
图4 分类变量的对数累积风险函数

图5为各连续变量的Schoenfeld残差图，可以看出图中的拟合曲线基本以0为中心波动，满足比例风险假定。

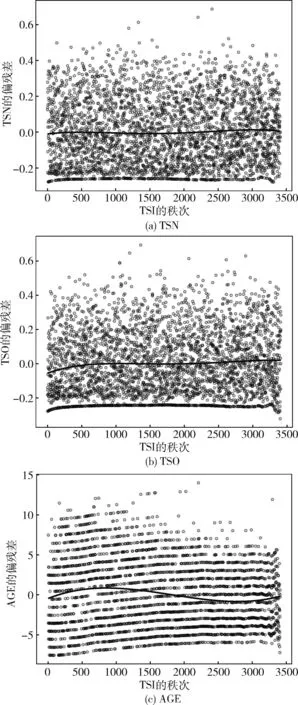
图5 连续变量的残差

表4中，维修模式、发动机和季度类型用虚拟变量表示。虚拟变量是指取值为0或1的变量，用于表示分类变量中某些属性状态是否存在。根据虚拟变量的设置规则，需要选取一种属性作为分析的基础，其它属性则作为虚拟变量进行分析。以“发动机型号”为例，CFM56-7B、CFM56-7B22、CFM56-7B24和CFM56-7B26这4种型号分别用Engine_1、Engine_2、Engine_3、Engine_4表示，将Engine_1作为参照变量，则Engine_2、Engine_3、Engine_4作为虚拟变量。各变量的系数为β中对应的值，P值表示该变量在设定的显著性水平(α=0.05)下是否显著，即该变量对基本失效率h0(t) 的影响是否显著。HR表示风险比，表示在其它变量保持一定时，该变量对基本失效率的影响程度。

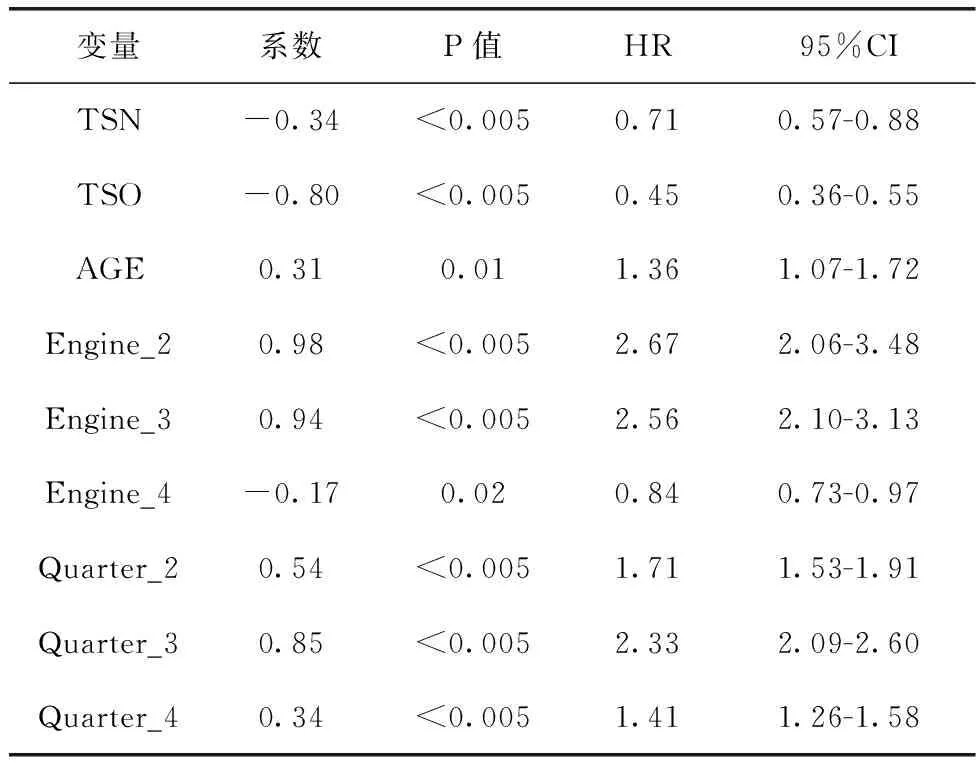
表4 比例风险回归结果

从表4中可以看出飞机机龄会使轮胎的故障风险增加；装有CFM56-7B22和CFM56-7B24的飞机上的轮胎更容易故障；第二季度和第三季度轮胎故障的风险更大。飞机轮胎值得注意的是TSN和TSO的HR值意味着当它们增加时轮胎的故障风险会降低，其主要的原因可能是由数据筛选的结果造成的。为了完整跟踪飞机轮胎从新件到经过数次维修后的连续状态，本文在数据筛选时选择了2016-2019期间使用的新轮胎的维修记录，因此数据中轮胎的累计飞行小时数不足。其次，航空公司现有的维修策略会要求一些部件在经过几次修理后就会经历一次大修，使得部件维修记录中的TSO值也不会太大。

3.3 剩余寿命预测结果分析

3.3.1 比例风险模型预测结果

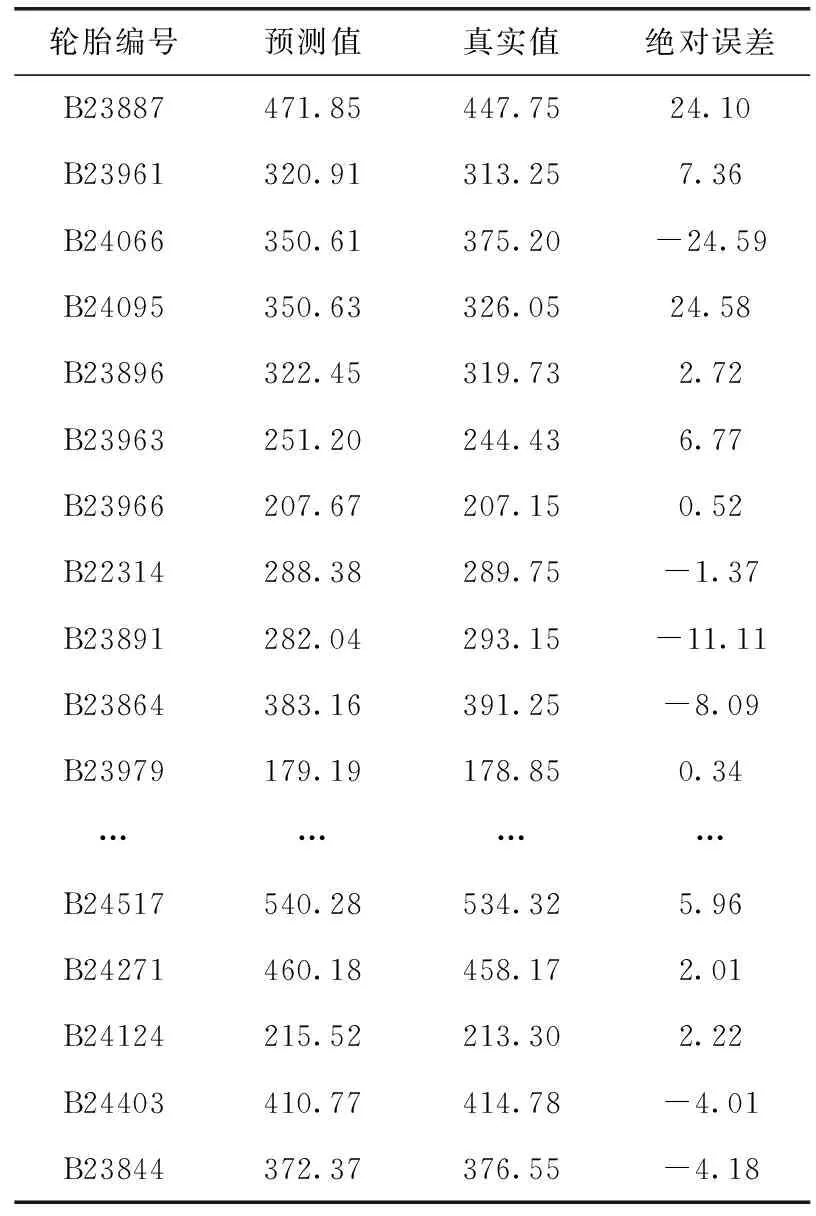
表5 比例风险模型预测结果

3.3.2 对比方法预测结果

为了更好地评估比例风险模型在预测部件剩余寿命时的效果，采用了其它回归模型进行对比，即将比例风险模型中的特征作为其它回归模型的参数。由于比例风险模型假设特征变量以乘积的形式影响基本失效率，包含了部件的寿命分布，因此本文在与其它传统回归方法对比时，考虑将部件的寿命信息加入到回归模型中。在文献[22]中，Kadhem等用威布尔分布对历史风速数据进行拟合，并用威布尔分布进行随机采样生成一个风速数据，通过将该数据与其它影响风速的特征作为人工神经网络的输入特征对风速进行预测。此外，在文献[23]中，He等提出了一种加性平均剩余寿命模型，分析了潜在风险因素对平均剩余寿命的影响。结合上述文献的数据处理思想，本文对分类回归树、多层感知机回归、多元线性回归、支持向量回归以及随机森林回归等其它回归模型分别尝试了如下两种不同的改进方法。

根据式(17)，在t1，t2，…，tn时刻计算出对应的平均剩余寿命m(ti)， 其中i=1，2，…，n。

(1)将m(ti) 加入到特征向量X中，作为第p+1个特征。然后将新的特征向量作为其它回归模型的输入。

(2)计算m(ti) 与实际剩余寿命的差值并作为因变量，然后将特征向量X作为其它回归模型的输入。

按照上述改进方法，使用训练集对各模型进行训练，测试集来验证各模型的预测能力。本文将均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分误差(MAPE)作为评估本文方法以及其它方法的指标。这些指标是预测任务中常用的评价指标，数学表达式如下

(20)

(21)

(22)

表6给出了比例风险模型与其它回归模型寿命预测的结果。其中L表示未改进的回归模型，L1表示第一种改进，即将m(ti) 加入到特征向量X中，将新的特征向量作为其它回归模型的输入。L2表示第二种改进，即计算m(ti) 与实际剩余寿命的差值作为因变量，将特征向量X作为输入。

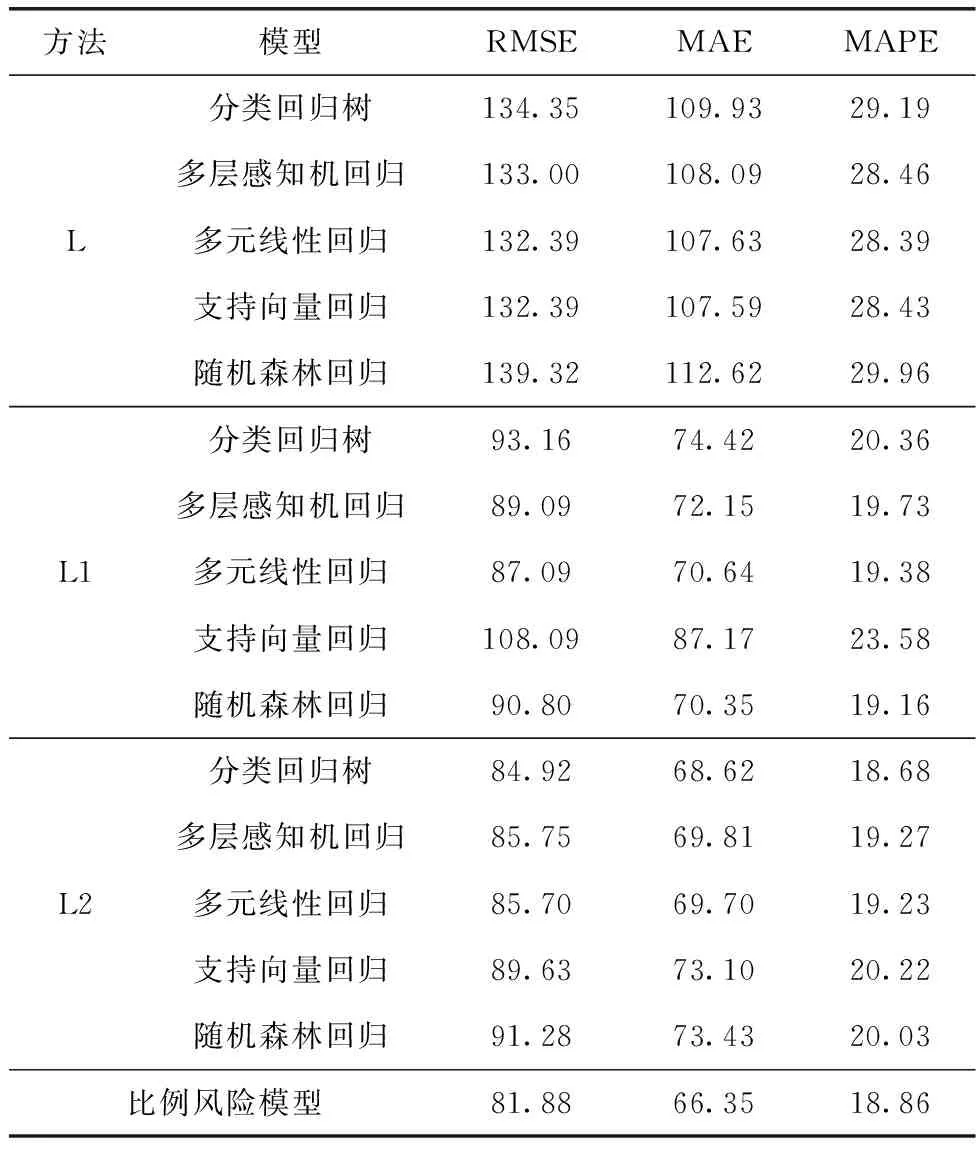
表6 各方法对比结果

可以看出改进后的回归模型预测精度有了明显提升。L1和L2相较L的RMSE分别降低了40.63以及46.83，MAE则分别降低了34.23以及38.24。从MAPE来看，L1和L2方法相较L在预测精度上分别平均提升了8.44%以及9.4%。而比例风险模型在3个指标上都要优于其它回归模型，在整体预测效果上，比例风险模型>L2>L1>L。

4 结束语

本文通过对飞机部件的维修数据进行分析，提出了基于比例风险模型的飞机部件剩余寿命预测方法。通过对飞机主轮进行实例验证，分析了影响飞机主轮寿命的主要因素以及影响程度，可为部件维修策略的调整提供参考。此外，通过对其它回归模型进行改进，提供了比例风险模型的对比方法。实验结果表明，改进后的回归模型的预测精度平均提升了8.92%，同时比例风险模型的整体预测效果要优于改进后的回归模型。