基于分布式多关联属性的高维数据差分隐私保护方法

褚治广，李俊燕，陈 昊，张 兴

(1.北京工业大学 信息学部，北京 100124；2.辽宁工业大学 辽宁省工业互联网网络与数据安全重点实验室，辽宁 锦州 121001)

0 引 言

在大数据的背景下，数据比以往更加的复杂，现实生活中更多的数据以高维的形式呈现。为此，充分挖掘高维数据的有用信息已经成为研究的热点，但目前在对高维数据进行挖掘时常常忽略隐私的重要性，从而导致大量用户隐私泄露。另外，通过关联规则对高维数据进行挖掘的过程中，不仅要考虑敏感属性还要考虑多种关联属性的影响[1]。例如，城市医疗大数据除了姓名、收入、家庭住址、疾病等敏感属性，一些通过关联分析得到的关联属性如阶级层级、购物倾向等也会间接暴露患者的隐私信息，从而对病人的生活和身心健康造成危害。因此，如何确保在高效挖掘高维数据的同时保证用户的隐私不被泄露成为日趋关注的焦点。

高维数据分析离不开降维[2]，文献[3]利用Pawlak属性约简算法求出核属性并通过启发式扩展得到一个约简，该约简算法可有效剔除高维数据中的冗余信息，得到分类规则，但核属性求解过程很麻烦。文献[4]针对医疗数据，结合差分隐私和粗糙集提取规则，提出了一种挖掘医疗数据隐藏模式并保证患者隐私的新方法(DPRers)。该算法在数据挖掘过程中增加拉普拉斯噪声实现差分隐私保护。只考虑了属性之间的隐藏特性，针对关联属性没有考虑，且上述方法对于高维大数据不能有效的处理。在分布式环境下，欧阳佳等[6]提出了一种基于差分隐私的数据发布方法，该方法采用分类讨论的思想，提高了数据的可用性。即对全局采用安全数据积协议，对局部运用基于组合的定理。文献[7]在分布式Hadoop框架下进行并行计算实现差分隐私关联规则挖掘算法，但因为Hadoop不是内存级别的处理方式，每次读取都需要存入HDFS中，存在大量IO操作，耗时较长。目前已有多种高维数据隐私保护方法[11-15]被提出，但隐私性和效用性仍无法有效平衡。文献[8]针对多源数据，以树结构优化存储，先利用频繁项集发布数据，再使用拉普拉斯机制和指数机制在数据发布的过程中进行保护，提高了发布数据的安全性，但该方法随着数据拥有者的增多，噪声的添加量也随之增加，从而使得数据的效用性降低。因此文献[9]利用启发式截断来降低全局敏感度，从而提高算法的可用性。同年，何文竹等[10]利用信息熵实现了结构化数据集的敏感属性的分类分级保护，同时兼顾属性的相关性和关联关系，但该方法在大规模数据集中的表现不佳。

由上可知，当前高维数据发布方法都存在一些缺陷，一方面高维数据存在维度灾难，导致一些传统的数据挖掘方法很难起作用且处理效率很低，另一方面数据维度越多，数据的关联性也会越高，会存在通过关联数据推测出其它数据的危险，使用传统的差分隐私进行保护，其保护水平往往很低，原因是维度越高的数据使用的噪声越多，过多噪声会造成数据的严重失真，并且可能会破坏属性间的关联性，可用性效果就会变差。因此我们提出一种基于分布式的多关联属性高维数据隐私保护方法(HDMPDP)，文章的贡献主要有：

(1)本文利用主流的Spark分布式处理框架在分布式条件下，采用分块的处理方式，利用邻域粗糙集理论实现高效的数据降维同时提高了数据的处理效率。

(2)利用改进的关联分析方法提取数据间的关联规则，在关联数据类中，针对敏感数据，使用敏感度划分隐私保护的需求等级，并采用属性信息熵作为敏感度衡量标准。

(3)应用信息熵对虚假的关联属性进行剔除同时对前面得到的不同属性关联度进行划分，从而使添加的噪声更合理。实验验证，HDMPDP方法在分布式条件下，通过上述两方面的处理，在得到更加有效规则的情况下也能有效提升高维数据的隐私保护程度。

1 差分隐私

差分隐私保护方法通过对输出的结果添加适当的噪声实现对原始数据集的扰动，消除掉数据的个性特征，保护数据的隐私。差分隐私严格的数学定义如下：

定理1ε-差分隐私(ε-differentail prvacy)：对兄弟数据集D1和D2(相差一条记录)，及其所有子集S，有随机算法A，满足式(1)

Pr[A(D1)∈S]≤eεPr[A(D2)∈S]

(1)

则算法A满足ε-差分隐私，称ε为隐私预算(衡量隐私保护程度)。差分隐私可以通过拉普拉斯机制(数值型)和指数机制(离散型)等进行实现。拉普拉斯机制通过添加噪声，指数机制根据敏感度和隐私预算，计算各数据的权重进行选择发布。两种机制都依靠全局敏感度，接下来将介绍全局敏感度。

定义1 全局敏感度(global sensitivity)：给定查询函数，D为输入数据集，f(D) 为输出数据集。在任意一对D1和D2上，函数的全局敏感度如式(2)所示

(2)

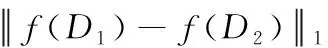
定理2 拉普拉斯机制(Laplace mechanism)：给定数据集D和隐私预算ε，函数f的全局敏感度为Δf，当f的输出满足

A(D)=f(D)+Lap(Δf/ε)

(3)

则称算法A满足ε-差分隐私，其中Lap(Δf/ε) 为满足Laplace分布的随机噪声。Laplace分布如图1所示。

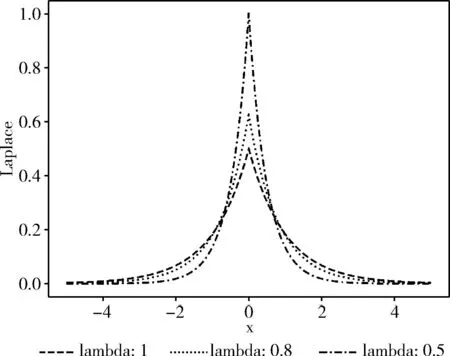
图1 Laplace分布

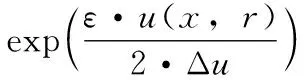
2 分布式多关联属性隐私保护方法

HDMPDP方法与文献[15]中提到的基于Hadoop处理方案不同，Spark是基于内存级别的高效处理方案，避免了把中间过程存储到分布式文件存储HDFS中，从而较少大量IO操作能有效提高算法的执行效率，如图2为Spark运行架构图。因此本方案拟在分布式计算框架Spark中进行实现，针对高维数据计算开销大，运算速度慢的情况，采用多处理机进行计算，提高运行效率的同时，更符合现在化的处理模式。

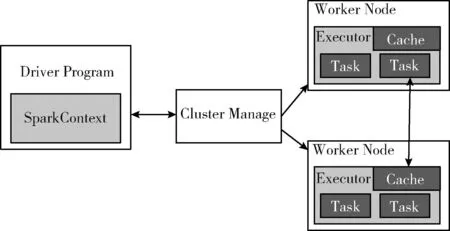
图2 Spark运行架构

2.1 基于分布式的粗糙集降维

搭建Spark集群利用分布式计算框架如图2所示，采用RDD(弹性分布式计算)的数据结构，把采集到的数据集保存在内存中，并且通过控制数据集的分区来达到数据存放处理最优化，这里分成多个Block，再针对每个Block分别进行数据的降维处理。

粗糙集理论是用于处理不确定关系的一种数学工具。将粗糙集用于高维数据降维能更好的保持原始数据的数据结构不丢失，但它仅适用于离散型数据，对于连续型数据并不适用。于是针对连续性数据采用邻域粗糙集来扩展粗糙集的引用范围，在粗糙集理论中，知识的表达是用决策系统表示的，一个决策系统由一个四元组表示

DS=(U，A，V，f)

其中论域U代表全体对象，A为属性全体，V则为属性的值域，f代表一个信息函数。具体含义可见文献[3]。

于是对于每一个Block首先将数据分成离散型和连续型两类，对于离散型数据根据粗糙集理论中不可区分关系与等价类的定义，计算出每个属性的等价类；然后根据式(4)和式(5)计算得到每个属性针对其它不同取值属性的上、下近似

(4)

(5)

其中，R为A的任意一个子集，且 [x]R={y∈U|(x，y)∈R}。 在这里数据属性间的关联性可以用粗糙集中属性依赖度k进行定量的度量(k=1表示D完全依赖C，k=0表示两者没有依赖关系)，由式(6)计算得到各个属性的属性依赖度关系再针对不同的属性添加合理的噪声。假设B⊆C， 定义决策属性集合D对B的属性依赖度的公式为

(6)

再利用式(7)计算互信息量，求出相对核CORE。采用互信息的属性约简算法可以有效把高维数据中不相关的冗余信息剔除，得到更合理分类规则，对于连续型数据则采用邻域粗糙集实现属性约简过程

I(C，D)=H(D)-H(D|C)

(7)

采用粗糙集理论实现高维数据降维的同时，利用属性间的依赖度作为属性关联度。根据所需数据维度以及分类效果设置不同阈值δ1， 计算得到的属性之间的关联度进行属性分类。

2.2 基于信息熵改进的关联分析

通过关联分析挖掘将发现大量存在于数据集中隐藏关联性的信息，进而得到某些能推测出敏感属性的关联属性集，为此，可对该属性集添加合理噪声从而实现差分隐私保护。

一般关联分析包含两个过程：即从数据集中寻找频繁项集(支持度)，从频繁项集中生成关联规则(置信度)。

支持度：某项集在数据集中出现的概率

support(A)=count(A)/count(dataset)=P(A)

置信度：项集A发生时，则项集B发生的概率。置信度体现的是关联规则的可靠程度，如果关联规则{A->B}的置信度较高，则说明当A发生时，B有很大概率也会发生，这样就可能会带来研究价值

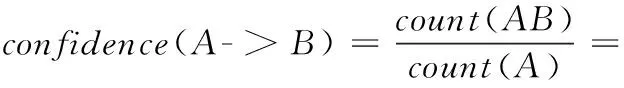
Apriori算法是经典的关联分析算法，一般只用于单维、单层的关联规则，对多维的规则并不适用。就多维数据而言，常采用FP-Tree算法得到多维规则，可以更加高效的挖掘频繁项集，但仍存在挖掘时间较长且有大量无效或冗余规则的问题，因此本文在分布式环境下采用属性信息熵优化针对粗糙集降维后的数据进行二次筛选，剔除冗余项，提高算法的执行效率。

在分布式条件下对于每一个Blcok实现属性分组后，再进行一次改进的满足差分隐私的关联分析，目的是寻找各个Block对应项目集合或对象集合间的频繁模式、关联性。属性信息熵H(P)常常用来描述信息出现的不确定程度，如式(8)所示

(8)

式中的对数一般取2为底，单位为比特。

针对高维情况，假设一事件由n个维度属性描述，则它第i个维度属性信息熵用式(9)中的Ei表示

Ei=-∑x∈XiPi(x)log2(PI(x))，i=1，2，…，n

(9)

式中：Xi代表第i个指标的属性集合，Pi(x) 是第i维中x发生的概率。

在关联数据类中，针对敏感数据，将根据敏感度划分隐私保护的需求等级，采用属性信息熵作为敏感度衡量标准。利用属性信息熵对不确定性进行度量，剔除虚假的关联属性还可以对前面得到的不同属性关联度进行划分，设置分类阈值δ2， 对大于阈值的规则进行剔除，从而保证规则的有效性。

2.3 算法描述

本文提出的算法专注于高维数据集中属性数据的发布。整个处理流程主要包含两大环节。首先，在分布式环境下，运用经过优化的粗糙集理论对原始数据集实施降维操作，以降低数据处理的复杂性和计算成本。其次，本文采用经过改进的关联分析算法，并结合差分隐私技术，对经过降维处理的数据集进行噪声添加，确保输出的数据集满足差分隐私保护要求，从而在保证数据可用性的同时，有效保护用户的隐私信息。整体流程如图3所示，算法具体流程如下：

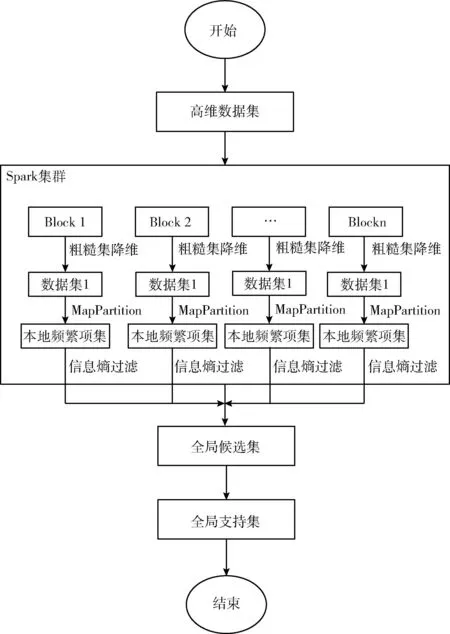
图3 算法流程

算法1：基于分布式的粗糙集降维

输入：DS，Blcok数，阈值δ1

输出：降维后的数据集O

(1)对DS按照输入的Block数进行划分，把连续型和离散型划分到不同的Block中；

(2)根据粗糙集理论中不可区分关系与等价类的定义，计算出每个属性的等价类；

(3)针对每个Block遍历每个属性，得到相应属性的等价类，利用式(4)和式(5)，计算每个属性相对于其它属性的上近似和下近似，以确定它们的等价类；

(4)由式(6)计算得到属性依赖度，用属性间的依赖度作为属性关联度；

(5)由式(7)计算互信息量，令O为空，求出COREC(D)；

(6)根据所需数据维度以及分类效果设置不同阈值δ1， 根据计算得到属性之间的关联度，实现属性的分类；

(7)在每个Block中得到分类子集，直到属性关联度小于δ1， 返回降维后的属性集O；

(8)算法结束。

算法2：基于信息熵的关联分析和敏感属性集的差分隐私保护

输入：降维后的数据集O，最小加权支持度min_sup，置信度，阈值δ2

输出：满足差分隐私的数据集O′

(1)对降维后的数据集O针对每一个Block进行关联分析；

(2)采用改进的FP-Growth算法进行关联数据挖掘，扫描数据集O；

(3)由式(9)计算不同Block中的属性信息熵，根据其维度进行加权处理，由min_sup生成频繁1-项集；

(4)扫描数据集，若有相同子节点则支持度计数加一，否则新建一个节点。最终生成一棵FP-Tree；

(5)由FP-Tree挖掘递归生成频繁项集，根据设定的置信度，生成关联规则；

(6)同时，根据属性信息熵，对小于阈值δ2的无效规则进行剔除；

(7)将粗糙集和信息熵得到的属性和关联分析得到的关联属性分别进行加噪。得到与敏感属性关联度高的非敏感属性数据，并将噪声平均分配到其每一个属性中。对于非关联数据类中的敏感数据，按照设定隐私保护需求等级的比例将噪声分配到敏感属性；针对属性无关的非敏感数据，则不添加噪声。

(8)生成满足差分隐私的数据集O′。

3 实验结果与分析

3.1 实验环境与数据集

为了测试本文算法的性能，实验使用Java实现，搭建Hadoop 2.7.2和Spark 3.0分布式集群，节点个数为4，在3.30 GHz GPU、16RAM的Centos7.0操作系统上运行，采用1994年美国人口普查真实数据集Adult数据集，数据集样本数量为45 222个，每个样本包含15个属性信息。其中有6个连续型属性，9个离散型属性。Adult数据集见表1。

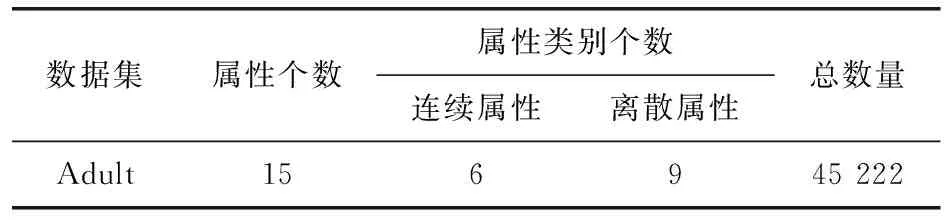
表1 数据集

3.2 算法评估标准

本文在分布式条件下综合考虑了数据间的多种关联关

系，包括属性关联性和规则关联性再结合差分隐私技术添加合理的噪声实现多维数据的隐私保护数据发布，因此实验主要分析算法的数据可用性、隐私保护程度和执行效率等因素。

针对数据可用性方面采用误分率进行衡量，即原始数据集上的查询和添加噪声后查询的绝对值和累加和。error值越小，表明原始记录与差分隐私保护后的误分类越低，数据信息损失越少。如式(10)所示

(10)

式中：e(A*) 和e(A) 分别代表有无噪声添加。

针对隐私保护程度方面采用数据披露风险记录关联(RL)来度量，即采用差分隐私处理后的数据集正确匹配原始数据记录的比例，如式(11)所示

(11)

式中：O′代表差分隐私保护后的数据记录，如果不在记录中则Pr(O′)=0，n为记录数。经差分隐私保护处理后的记录与原记录之间的匹配率越低，表明两者关联性减弱，数据信息泄露的风险将越低。即RL值越小，数据信息泄露的可能性越小，保护性越好。

针对执行效率方面采用加速比来测试算法的并行效率。即在相同任务量下，单一处理器与多处理器花费时间的比值。该值越大表示并行计算过程中所消耗的时间越少，执行效率越高。如式(12)所示

(12)

式中：Ts和Tc分别代表单机和集群的运行时间。

3.3 实验结果与分析

针对HDMPDP算法，设定隐私预算ε分别为0.01，0.3，0.6，0.8，1.0。一般隐私预算越小说明数据中注入的噪声越多，隐私保护程度越高，数据损失就越大。对比OBDP和PrivBayes算法进行实验对比，两者均采用贝叶斯网络实现高维数据的降维，前者是对后者采用互信息优化贝叶斯网络的构建过程。则3类算法造成的误分类Error如图4所示。

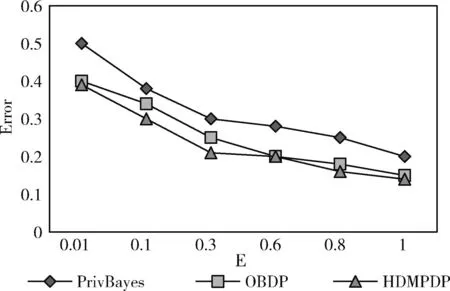
图4 ε取不同值时，Error变化情况

图4展示了3类算法在不同隐私预算下的分类误差。实验结果表明，随着隐私预算的增加，3类算法的隐私误差都呈现减小的趋势，隐私保护程度都在增加。本文的HDMPDP方法稍优于其它两种方法，因为该算法只针对敏感属性和满足一定条件的非敏感属性进行了隐私保护处理，考虑到不满足条件的非敏感数据对隐私泄露的影响较小，无需再分配额外的隐私预算，数据集整体添加的噪声量减少，数据的效用性也随之增加。

为了验证本文提出算法的有效性，使用此算法验证发布数据的可用性和数据信息的安全性，将HDMPDP算法与同类算法在Adult数据集上进行对比，衡量指标为信息损失大小和数据泄露风险。实验设置设定隐私预算分别为0.01、0.2、0.4、0.8、1.0，分别对比HDMPDP算法与基于Hadoop算法的RL值，结果如图5所示。

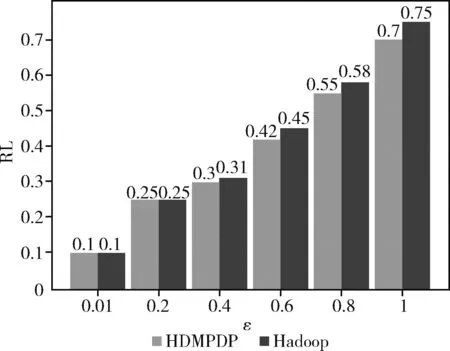
图5 ε取不同值时，RL值变化情况

由图5可知，当隐私预算ε设定为0.01时，RL值达到最低点，表示此时隐私泄露的风险最小。这是因为在数据中加入了大量的噪声，从而保护了隐私。然而，这种大量的噪声也导致了数据可用性的降低。当隐私预算增加到0.2和0.4时，无论是采用本文提出的HDMPDP算法还是传统的Hadoop算法，RL值都相近，表明两种算法在此时的隐私保护效果相当。当隐私预算超过0.4后，随着预算的增加，RL值急剧上升，这意味着数据泄露的风险也随之增大。但本文算法的数据泄露风险还是较低些，因此综合考虑数据可用性和数据泄露风险，本文的HDMPDP算法在取0.4时算法性能最优。

为验证HDMPDP算法执行的效率，本节对其算法加速比进行衡量。我们取在隐私预算为0.4的情况下，分别在数据集下将HDMPDP算法与基于MR的算法的运行时间进行对比，独立运行10次后各取其平均值。通过对比运行时间，可对HDMPDP算法的性能进行评估，结果如图6所示。

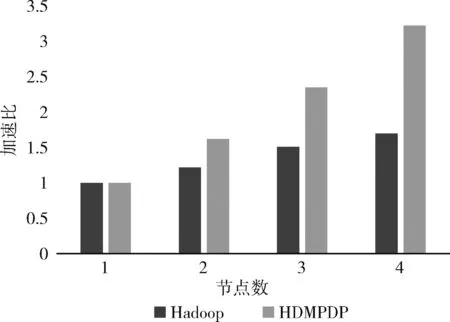
图6 节点数对加速比的影响

从图6中可以看出，随着节点数量的增多，HDMPDP算法产生了较高的加速比，运行时间不断减少，性能表现最佳。由此可说明本文使用的Spark框架分布式计算在迭代运算效率方面高于MapReduce框架。

4 结束语

本文研究了高维数据多关联属性的隐私保护问题，提出了一种新的分布式环境下针对高维数据和多关联属性的隐私保护方法(HDMPDP)。首先采用Spark框架对传统的降维方法进行了改进，利用互信息进行第一次特征筛选，使用属性间的依赖度作为属性关联度，减少降维过程中的信息损失，同时提升处理效率。其次在降维后的数据处理阶段，本文运用了基于信息熵优化的关联分析方法进行深入挖掘，为了确保数据隐私不被泄露，对分类后的数据集进行差分隐私保护。通过实验验证，本文提出的HDMPDP算法与同类算法相比，能在保证数据泄露风险较小的情况下，提升算法的运行效率，提高数据的可用性。但是本文在算法的优劣评价，没有一个明确的标准。对于评价标准的确定有待日后的进一步研究；并且文中针对隐私预算的分配采用了均分原则，这样可能会造成隐私预算分配的不合理从而降低隐私保护的效率。因此，下一阶段主要研究的目标是，设计不同的隐私分配方案以及再更加复杂的数据集上解决高维数据的发布效率问题。