结合稀疏先验与多模式分解的低秩张量恢复方法
杨秀红,苟田坤,薛怡,金海燕,2,石争浩,2
1.西安理工大学计算机科学与工程学院,西安 710048;2.陕西省网络计算与安全技术重点实验室,西安 710048
0 引言
张量作为向量和矩阵的多维扩展,在现实生活中发挥着越来越重要的作用,例如,视频图像、高光谱成像(刘盛 等,2021)、磁共振成像(Yama 等,2020)和计算机断层扫描(Zhang 等,2020b)等。然而,在实际应用中,由于获得的张量数据可能是不完整的,严重降低数据质量以及限制应用。张量补全(tensor completion,TC)旨在从不完整的观测中恢复缺失条目,在计算成像中有许多应用,如高光谱图像恢复(杨润宇 等,2019)、彩色图像/视频补全(Jiang等,2023;Qin 等,2022)和人脸识别(Fu 等,2019)。对于这种不适定性逆问题,当考虑缺失元素和已观测元素之间的关系时,与矩阵数据的结构先验相比,张量数据的结构先验信息是复杂的,往往难以确定(Cichocki 等,2017)。张量数据能够描述真实世界中多个数据通道之间结构特征的耦合,相对低维的相关特征信息被嵌入了更高维的度量中,因而结构先验信息的表示比矩阵数据更加复杂。
张量分解可有效挖掘张量数据的内在特征,但传统分解方法诱导的张量秩函数无法探索张量不同模式之间的相关性;另外,传统张量补全方法通常将全变分约束施加于整体张量数据,无法充分利用张量低维子空间的平滑先验。为了解决这两个问题,本文旨在有效提取关于潜在张量结构的有用信息,以提高缺失元素的恢复性能。
1 相关研究现状
张量秩最小化方法在TC 中有着广泛的应用。然而,与矩阵秩不同,张量秩的定义并不是唯一的。基于不同的张量分解,张量秩有不同的定义。Tucker秩可以定义为张量沿着每个模式展开矩阵秩的多线性组合。HaLRTC(high accuracy low-rank tensor completion)(Liu 等,2013)将矩阵核范数扩展到高维张量,建立沿着张量每个模式方向的展开矩阵秩之和(sum-of-nuclear-norms,SNN),并将SNN 作为Tucker 秩函数的凸近似,同时将张量补全表示为一个凸优化问题。Mu 等人(2014)证明了将SNN 作为张量秩函数的凸松弛是次优的,因此为缩减SNN 与非凸模型之间的差距,提出一种更适合的凸松弛,在保持张量低秩性的同时,将张量展开成一组更平衡的矩阵。然而,现有的方法与非凸模型相比,时间、计算复杂度仍然不是最优的,并不适合处理大规模张量数据。Han等人(2017)受矩阵截断核范数(Guo等,2017)启发,提出一种张量截断核范数,并在目标函数中定义了一个多维离散余弦变换的1-范数约束的稀疏正则化项。基于张量奇异值分解(tensor singular value decomposition,T-SVD)的多线性秩和张量管秩可用于构造张量秩最小化模型,Song 等人(2020)提出基于变换的张量管秩,使用酉变换代替传统张量奇异值分解中的离散傅里叶变换,可以得到更低的张量管秩,对于鲁棒性张量补全更加有效。张量管核范数的部分和(partial sum of tubal nuclear norm,PSTNN)(Jiang 等,2020)研究了T-SVD(tensor singular value decomposition)框架下的张量恢复问题,即提出张量管核范数的部分和(PSTNN)作为张量管多秩的替代物,建立了基于PSTNN 的张量恢复模型。Chen等人(2021)提出一种基于自动加权机制的张量链秩鲁棒性补全模型,该模型可利用一个自动加权机制来平衡同一张量中不同矩阵的重要性。传统的基于张量环分解模型对于张量秩的选择非常敏感,因此,Long等人(2021)提出了一种基于贝叶斯方法的低秩张量环补全方法,通过自动学习数据的低秩结构来恢复图像。利用稀疏诱导的分层先验约束因子张量的水平切片和正向切片,采用贝叶斯推理得到张量环秩。然而这些传统的方法只能独立地利用张量每个模式的低秩性,无法有效利用张量多个维度之间紧密的多线性相互作用的先验知识。
低秩张量分解(low-rank tensor decomposition,LRTD)是TC 的另一条研究主线,它可以解决张量秩最小化的部分缺点。然而,LRTD 面临的挑战是设计一个合适的分解模型来表示不完整张量的低秩结构。Tucker 分解(Tucker 等,1966)是指将一个张量分解为一个核张量以及一组因子矩阵的模式乘积之和。随着张量缺失条目的增加,因子分解方案可能会因错误预设秩大小,从而导致过拟合现象。为了解决这一难题,并实现在补全张量的同时捕获底层的模型结构。Chen 等人(2014)提出一种在张量补全的同时进行张量分解的方法(simultaneous tensor decomposition and completion,STDC)。TRLRF(tensor ring low-rank factors)(Yuan 等,2019a)建立了多线性张量秩与TR(tensor ring)因子秩之间的理论关系,使得低秩约束可以隐式地在TR 潜在空间上进行。Zeng(2021)通过对Tucker 分解的深入研究,提出一种新的基于多模式核张量分解的低秩张量补全模型,同时提出该模型的非凸松弛形式。统计先验的帮助下,最近的LRTD 方法利用贝叶斯框架来增强TC 模型,Zhang 等人(2019)提出一种基于自适应低秩表示的张量补全模型,在贝叶斯框架中分别表示潜在的张量低秩和非低秩结构。在T-SVD分解框架(Zhang 和Aeron,2017)中,张量数据可以用一个定义的张量乘积算子来表示,元素之间具有循环卷积和乘法运算。基于张量奇异值分解(Lu 等,2020;Zhang 等,2019)下张量多秩和张量管秩的定义,建立了张量恢复模型。张量链分解(Oseledets,2011)是一种高级张量网络分解模型,可将高维张量分解为一系列三维核张量,这些核张量相互作用,在张量补全领域中有着广泛的应用。Yuan 等人(2019b)提出两种基于张量链分解的张量补全算法,分别是张量链加权优化(tensor train weighted optimization,TTWOPT)和张量链随机梯度下降(tensor train stochastic gradient descent,TT-SGD)优化张量链分解因子,用以捕获张量数据的潜在特征,重构缺失数据。然而,张量链分解和张量环分解只能建立相邻两个分解因子之间的联系,并且对张量模式排列方式特别敏感,无法灵活地表示张量。因此,Zheng 等人(2021)提出全连接张量网络分解。全连接张量网络分解的优势在于能够充分描述任意两种张量模式之间的内在关联,并具有充分表征全局相关性和保持其换位不变性的能力。
低秩分解作为一种强大的张量分析工具,在深度学习领域也有着广泛的应用。Hou 等人(2017)为解决遥感图像检测问题,提出了一种基于低秩的显著性计算和深度特征表示方法。利用卷积神经网络(convolutional neural network,CNN)提取超像素特征,并对两幅输入图像的变化特征进行低秩分解,生成显著性映射,表示每个像素的变化概率。Luo 等人(2022)提出一种非线性多层神经网络,仅利用观测张量来学习非线性变换。该网络利用变换张量的低秩表示和观测张量与重构张量之间的数据拟合来学习非线性变换。Wang 等人(2022)提出了一种新的基于耦合非线性变换(coupled nonlinear transform,CoNoT)的低秩张量表示,以获得更好的低秩近似,并使用CNN 作为CoNoT,它可以以无监督的方式仅从观察到的多维图像中学习。针对现有张量补全方法在表征低秩结构方面的能力有限问题,Xue 等人(2022)提出一种基于稀疏性的多层张量分解(multilayer sparsity-based tensor decomposition,MLSTD)方法,以描述具有隐藏在张量中的隐式稀疏属性的复杂层次知识,提高低秩张量补全的效果。Yu和Yang(2023)定义了一个新的非凸张量伪范数来代替张量核范数的加权和(weighted sum of the tensor nuclear norm,WSTNN)作为更紧秩近似,然后引入时空矩阵以利用低秩静态背景和稀疏前景的固有时空特征,最后引入了一个非相干项来约束稀疏前景和动态背景以提高可分性。
全变分(total variation,TV)(Chen 和Zhang 等,2021)正则化是一种图像去噪和图像恢复技术,通过对图像灰度级梯度度量,可描述图像的边缘和纹理信息,为图像处理(He 等,2019)和模式识别(Zhang等,2020a)应用提供了新思路。在TC 问题中,TV 项通常被纳入到一个低秩框架中,以便表征在不同维度上的局部分段平滑特性和全局低秩结构,比较典型的工作有MF-TV(matrix factorization-total variation)(Ji 等,2016)和LRTC-TV-II(low-rank tensor completion total variation-II)(Li 等,2017;Ko 等,2020)。Wang等人(2018)提出一种基于各向异性空间光谱全变分正则化(anisotropic spatial-spectral total variation,SSTV)与Tucker 分解的高光谱图像去噪算法。在全变分的基础之上,Yang 等人(2022)提出将分数阶有界变分空间中的分数阶全变分纳入至低秩张量补全模型中,以便高效恢复高损失率的多通道视觉图像。然而,基于TV的张量局部稀疏性的描述无法利用张量子空间稀疏先验知识。
本文在张量秩最小化基础上,融入多模式张量分解技术描述全局低秩特性;对于张量局部稀疏性,本文在多模式张量分解框架中假设因子矩阵具有潜在的局部分段平滑特性,即利用因子梯度稀疏性衡量局部稀疏性。基于以上两点,提出了一个结合全局低秩性与局部稀疏性的张量恢复模型,主要贡献如下:1)受多模式核张量分解技术的启发,将多模式张量分解技术与张量秩最小化思想相结合,可以有效利用张量不同模式之间的相关性。2)利用多模式张量分解模型的因子梯度稀疏先验作为有效约束,来表征张量的底层子空间局部结构的稀疏性。3)提出一种稀疏先验多模式张量分解恢复模型,同时利用张量的全局低秩性与局部稀疏性来恢复受损的张量数据。其中,对原始张量施加核范数约束,以此捕获张量的全局低秩性,并对因子矩阵施加因子梯度稀疏正则化约束,以便探索张量子空间的局部稀疏性,从而进一步提高了张量恢复性能。
最终,本文采用一种基于乘子交替方向法(alternating direction method of multipliers,ADMM)(Boyd 等,2011)的有效优化算法来求解所提模型,其中每个变量和相关参数都可以通过求解封闭子问题进行更新。
另外,本文模型可应用于深度学习网络的轻量化中。例如:对张量数据在局部稀疏性的约束下进行低秩分解,采用结构化蒸馏方式保留最主要的网络参数,去除冗余参数,在尽量保持网络性能的前提下,达到轻量级的目的,所以本文算法有着重要的研究价值。
2 相关工作
2.1 本文相关符号
为便于介绍本文方法以及张量代数,本小节统一规定所使用的符号。标量表示为小写字母,例如x,y;向量表示为粗体小写字母,例如x,y;矩阵表示为粗体大写字母,例如X,Y;张量表示为加粗花体字母,例如X,Y。对于两个大小相同的N阶张量,其内积可定义为,其Frobenius 范数定义为‖X‖F=。
张量模式-n排列:给定一个三阶张量其模式-n排列可定义为或permute(X,k),的第i个模式-3切片是X沿着模式-i方向的切片,即,其逆运算可定义为。
张量模式-n乘积:张量模式-n乘积可以看做是矩阵乘积向高维张量的扩展,对于X∈和矩阵U∈的模式-n乘积可以表示为Z=X×nU,张量X的模式-n乘积的展开形式可表示为。
2.2 相关工作
2.2.1 多模式张量分解
多模式张量分解可将整体张量沿着每个模式分解为一组低维张量和一组因子矩阵。对于一个三阶张量X∈,其多模式张量分解可定义为
式中,Cn为因子张量,An为因子矩阵。多模式张量分解如图1所示。
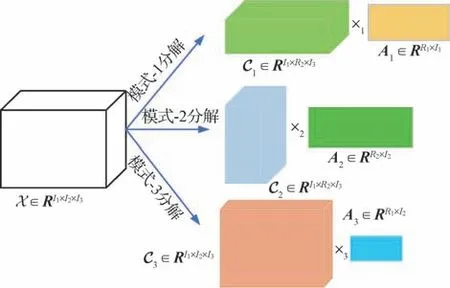
图1 三阶张量的多模式张量分解Fig.1 Multi-mode tensor factorization of a third-order tensor
2.2.2 张量秩最小化模型
基于张量秩最小化模型可表述为
式中,X是潜在的张量,M是观测到的张量,Ω则是观测元素的索引集。
张量秩有很多种形式,如Tucker秩、CP秩、TT秩和TR 秩等。由于直接描述张量秩是一个NP-hard问题,在矩阵补全中常常利用矩阵非零奇异值的数量,即核范数来代替矩阵秩函数。因此将核范数的概念推广至描述张量秩,优化模型(2)可以表述为
式中,‖·‖*为在不同张量分解技术诱导下产生的张量秩函数,即张量核范数。
基于张量秩最小化模型本质上是寻找张量秩函数的近似代替,将张量补全问题优化为张量核范数最小化问题,并试图在张量补全过程中,保持张量内部精细结构。在恢复不完整张量时,基于张量秩最小化模型比基于张量分解模型在准确度和效率方面表现更加突出。
3 本文方法
本节在张量秩最小化模型的基础上,提出结合稀疏先验与多模式张量分解的低秩张量恢复(sparsity prior multi-modal tensor factorization completion,SMTFC)方法。该方法核心思想是在张量秩最小化的同时,利用多模式张量分解技术处理张量不同模式方向的相关性,对整体张量施加低秩约束,以此捕获张量全局低秩特性,同时完成张量分解与张量恢复任务。此外,对多模式分解矩阵施加因子梯度平滑约束,以此探索张量低秩子空间的稀疏先验。
3.1 张量多模式相关性分析
传统的基于张量秩最小化的低秩张量补全模型是在张量低秩属性约束下,通过最小化张量秩优化恢复张量,张量秩可以是Tucker秩、TNN等。大量研究表明,张量数据的各个模式间具有相关性(Zheng等,2020),例如,高光谱图像是同一场景在不同光谱波段上产生的不同成像结果,这表明光谱图像在光谱维度中存在较高的相关性;一段视频包含多帧图像,在时间维度上不同的帧存在着高度相关。如图2所示,图2(a)为256×256×80 的Urban 高光谱图像,图2(b)是图2(a)沿着每个模式展开矩阵的奇异值曲线。
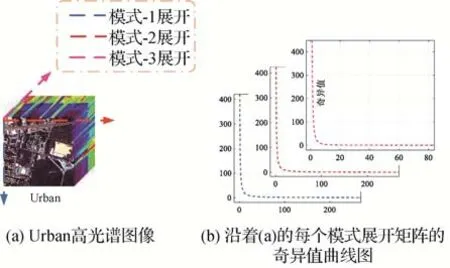
图2 张量不同模式之间的相关性Fig.2 Correlation between different modes of a tensor((a)Urban hyperspectral image;(b)singular value curve plot for unfolding matrix along each mode of(a))
从图2可以观察到,3种模式展开矩阵的奇异值都呈现锐减趋势,且只有一小部分奇异值大于零,这意味着张量在每个模式方向都是相关的,同时也反映了其在每个模式方向上均位于低秩子空间上。但Tucker分解诱导的Tucker秩和T-SVD诱导的TNN无法灵活处理张量的多模式相关性,因此将多模式张量分解技术融入张量秩最小化模型中,优化后的张量秩最小化模型可表示为
3.2 稀疏性分析
式(4)将低秩性推广至沿着张量每个模式方向的全局空间,称为张量全局低秩性,但其缺乏对张量局部信息的描述。对于一个张量,多模式张量分解框架中的每个因子矩阵都包含着与其相应模式的对应潜在信息,并揭示了模式内部和模式之间有价值的相关辅助信息。自然的张量数据通常具有局部稀疏性,例如高光谱图像中的道路和建筑等具有相似性,以及视频的帧之间具有较强的连续性,沿着时域方向静态背景的可重复性,这些均可以视为局部稀疏性。在数学上,对于给定的N阶张量X∈,其张量子空间局部稀疏性可表示为
式中,Ln∈为平滑矩阵,Ln(i,i)=1,Ln(i,i+1)=-1,平滑矩阵其他元素为零。p是选择稀疏性约束类型的参数,当p=1 时,f(An)为基于拉普拉斯分布的稀疏先验,当p=2 时,f(An)为基于高斯分布的稀疏先验。
为进一步验证局部稀疏先验有效性,在一个开源高光谱数据集上进行实验。图3 为一个三阶张量的多模式张量分解因子梯度稀疏性示意图。
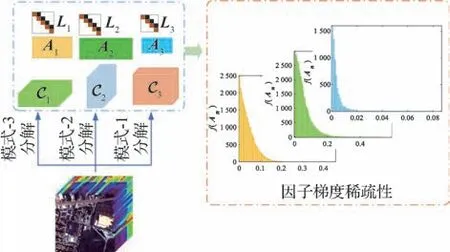
图3 三阶张量的多模式张量分解因子梯度稀疏性示意图Fig.3 Illustration of the gradient sparsity of the multi-mode tensor factorization factor for a third-order tensor
图3 左侧是大小为256×256×80 的Urban 高光谱数据集及其多模式张量分解示意图,右侧为因子梯度稀疏性示意图。在图3 中,因子梯度直方统计图的绝大多数因子梯度值为零或接近零,可以证明多模式张量分解因子具有局部稀疏性。
综上,本文在张量秩最小化模型的基础上,结合多模式张量分解与局部稀疏先验优化,构建SMTFC模型,即在张量潜在子空间假设的基础上,选择局部稀疏性先验用以保留局部分段的相似性。
SMTFC模型的目标函数表示为
式中,λn>0,τn>0为正则化参数,同样利用Frobenius范数约束,从而防止在优化迭代中过拟合。此外,与Xue等人(2022)方法相同,这里p=1。
4 整体算法流程
本节在稀疏先验与多模式张量分解的低秩张量恢复模型构建基础上,对张量恢复模型展开讨论,并对模型优化求解过程进行详细阐述,以便实现基于稀疏先验与多模式张量分解的低秩张量恢复任务。
4.1 模型说明
图4 为SMTFC 模型的整体流程示意图。如图4所示,本文算法首先通过多模式张量分解将不完整张量分解为一系列低维因子张量与因子矩阵,使用张量核范数对整体张量进行低秩约束,并利用张量奇异值分解对整体张量进一步分解。与此同时,为进一步探索张量潜在子空间的先验条件,对因子矩阵施加因子梯度稀疏正则化约束。通过对整体张量施加张量核范数约束,可有效捕获张量全局低秩特性,利用多模式张量分解可有效处理张量不同模式之间的相关性,同时因子梯度稀疏先验可充分利用张量潜在信息,从而进一步提高张量恢复性能。
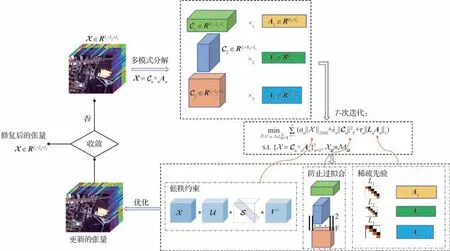
图4 SMTFC模型示意图Fig.4 Illustration of SMTFC model
4.2 求解过程
与LRTC-3DTV 模型优化求解过程相似,本节同样采用ADMM 技术求解优化该模型。在实际应用中为方便后续的优化求解,可以利用张量模式-n排列操作对原始张量进行permute 运算,即=permute(X,n),n=1,2,3。将模式-n乘积转化为模式-3 乘积,转化后的模式-n分解可表示为。因此,通过permute 运算优化后的式(6)可表述为
利用增广拉格朗日乘子法将式(8)优化为增广拉格朗日函数,即
式中,张量Wn,Tn以及矩阵均为拉格朗日乘子,ρ1,ρ2和ρ3为惩罚参数,随后通过以下解决方案更新各个变量。
这个最小化问题可以通过软阈值收缩运算解决,即
式中,shrinkageς(x)=sign(x).*max{|x|-ς,0},“.*”代表元素级乘积,x为矩阵中的一个元素。
对于上述优化子问题(13)可以视为sylvester 矩阵方程。
式中,F1为一维离散傅里叶变换(discrete fourier transform,DFT)矩阵。通过sylvester 矩阵方程快速求解法并结合式(13)可以求解式(12),即
式中,fold表示将H矩阵沿模-3折叠为张量。
上述优化子问题可以通过张量奇异值阈值算子(tensor singular value thresholding,t-SVT)解决,因此的求解方式可表示为
式中,Dς(Z)=U *Sς*VT,这里U,S,V为张量Z进行T-SVD 后产生的张量,Sς满足以下形式:,fft为傅里叶变换,ς为阈值。
5)更新变量X。通过固定其他变量,可得到关于X的优化子问题,即
因此,关于X的优化子问题可以利用如下优化方案解决,即
更新拉格朗日乘子Wn、Tn以及矩阵,具体计算为
输入:观测张量M,正则化参数αn、λn,观测张量条目索引Ω。
输出:恢复张量X。
2)fork=1,2,…,Kdo;
7)更新变量X,通过式(21)求解;
10)end。
5 实验与结果分析
本文将在高光谱图像(hyperspectral image,HSI)数据集、多光谱图像(multispectral image,MSI)数据集、MRI(magnetic resonance imaging)数据集以及YUV(也称YCbCr)视频数据集上进行对比实验。
1)实验环境。软件环境为windows11 64 位,MATLAB R2021b,实验硬件环境为AMD Ryzen 7 6800H处理器和16.0 GB RAM内存。
2)评估准则。本文将恢复张量数据的所有通道的PSNR(peak signal-to-noise ratio)和SSIM(structural similarity)分别取平均值,记为MPSNR 和MSSIM。PSNR的定义为
式中,MAX表示图像中最大的像素,MSE表示恢复图像与原始图像X的均方误差。MSE定义为
式中,N代表图像像素的总个数。
3)对比方法。选择HaLRTC(Liu等,2013)、LRTCTV-II(Li等,2017)、MF-TV(Ji等,2016)、TRLRF(Yuan,2019a)、PSTNN(Jiang 等,2020)、LPRN(solve the nonconvex LRTC model)(Yu 和Yang,2023)、LGNet(Quan等,2022)和GP-WLRR(global prior refined weighted low-rank representation)(Liao等,2024)作为对比方法。其中,后两种是深度学习的方法。在预训练参数的基础上,LGNet和GP-WLRR使用高光谱图像数据集、多光谱图像数据集、YUV视频图像数据集、fastMRI医学图像数据集进行参数微调,数据集均为200 幅图像。设置LGNet 的学习率为0.000 2,epoch 为100;GP-WLRR的学习率为0.000 1,epoch为100。
4)参数设置。对于所有的张量恢复模型,迭代停止阈值条件均为ε=1.0×10-6,最大迭代次数K=300。本文方法惩罚参数=1.0×10-2,调优参数β=1.1。与LRTC-TV-II相似,对于每组实验=1.0×103,=1,αn=。
5.1 高光谱图像
测试图像为Urban、Washington DC Mall 高光谱图像数据集,均由Hydice 传感器取得,其中原始Urban 图像数据集大小为307×307×210,去除严重吸水波段后大小为307×307×162,原始Washington DC Mall 图像数据集大小1 208×307×191。实验中Urban 和Washington DC Mall 高光谱图像数据集大小为256×256×80。每个高光谱数据均可视为3 阶张量,并将每个高光谱图像进行归一化处理。图5 为本次实验所使用到的高光谱图像数据集。其中,图5(a)(b)分别为高光谱图像数据集Urban 和Washington DC Mall的第70波段图像。

图5 高光谱图像数据集Fig.5 HSIs datasets((a)Urban;(b)Washington DC Mall)
实验中设置的3 种丢失率(missing rate,MR)分别为80%、90%、95%。为了验证不同方法在高光谱图像上的恢复性能,将从定量评价以及视觉评价的角度对不同的实验方法进行评估。
在客观评价指标方面,表1 为在各丢失率下不同恢复方法在Urban 以及Washington DC Mall 上恢复张量的MPSNR、MSSIM 值。如表1 所示,在所有实验方法中,SMTFC 模型在客观评价指标上均获得最佳的恢复精度。在统计意义上,SMTFC 模型获得最佳的恢复性能。
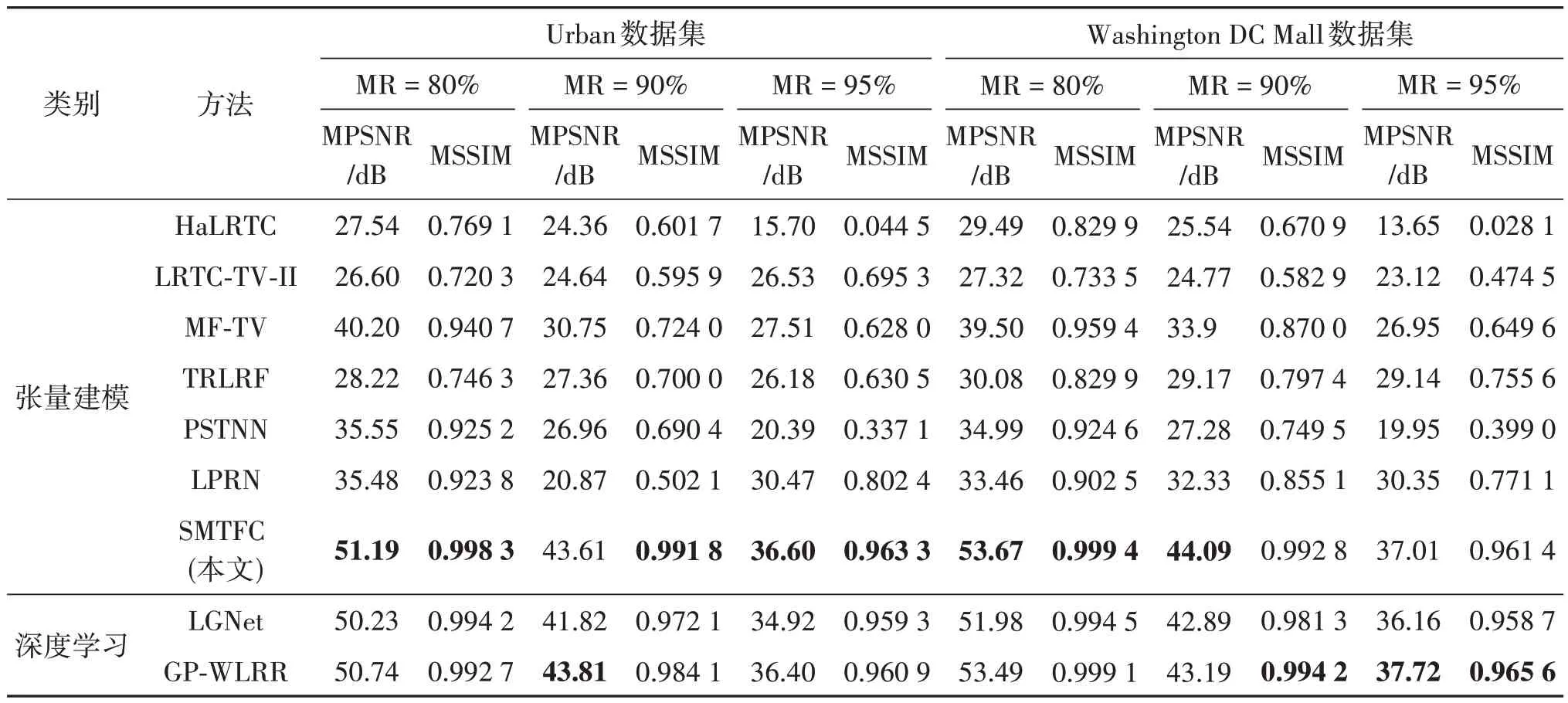
表1 不同恢复方法在高光谱图像上的定量比较Table 1 Quantitative comparison of different completion methods for HSIs
在主观视觉效果方面,图6 和图7 显示了当MR为90%时,不同方法在高光谱图像数据集Urban 和Washington DC Mall 的第70 光谱波段恢复结果的视觉评价,图中数值为PSNR 值。以Washington DC Mall 为例,TRLRF 和PSTNN 可以获得一定的视觉效果,而HaLRTC、LRTC-TV-II和MF-TV 由于在构建张量恢复模型时采用了张量矩阵化思想,破坏了张量复杂的高维内在结构,导致恢复结果的边缘模糊不清,无法精确恢复图像。SMTFC 模型的PSNR 值最高,恢复图像获得了良好的视觉效果,将局部细节放大,SMTFC 模型可以有效保留图像的边缘结构与精细的纹理结构,获得了最佳视觉效果。

图6 不同方法在高光谱图像数据集Urban上的视觉评价Fig.6 Visual evaluation of different completion methods on Urban dataset of HSIs

图7 不同方法在高光谱图像数据集Washington DC Mall上的视觉评价Fig.7 Visual evaluation of different completion methods on Washington DC Mall dataset of HSIs
5.2 多光谱图像
本小节测试图像来自CVAE(Columbia Imaging and Vision Laboratory),以Toy 和Feathers 为例,数据集尺寸均为256×256×31,将每个多光谱图像进行归一化处理,MR同样设置为80%、90%和95%。图8为本次实验多光谱图像数据集中Toy 和Feathers 的第30波段。

图8 多光谱图像数据集Fig.8 MSI datasets((a)Toy;(b)Feathers)
在客观评价指标方面,表2 为在各丢失率下,不同方法在Toy 和Feathers 上恢复张量的MPSNR、MSSIM值。如表2所示,在所有实验方法中,SMTFC模型在客观评价指标上均获得最佳的恢复精度。在统计意义上,SMTFC模型获得最佳的恢复性能。
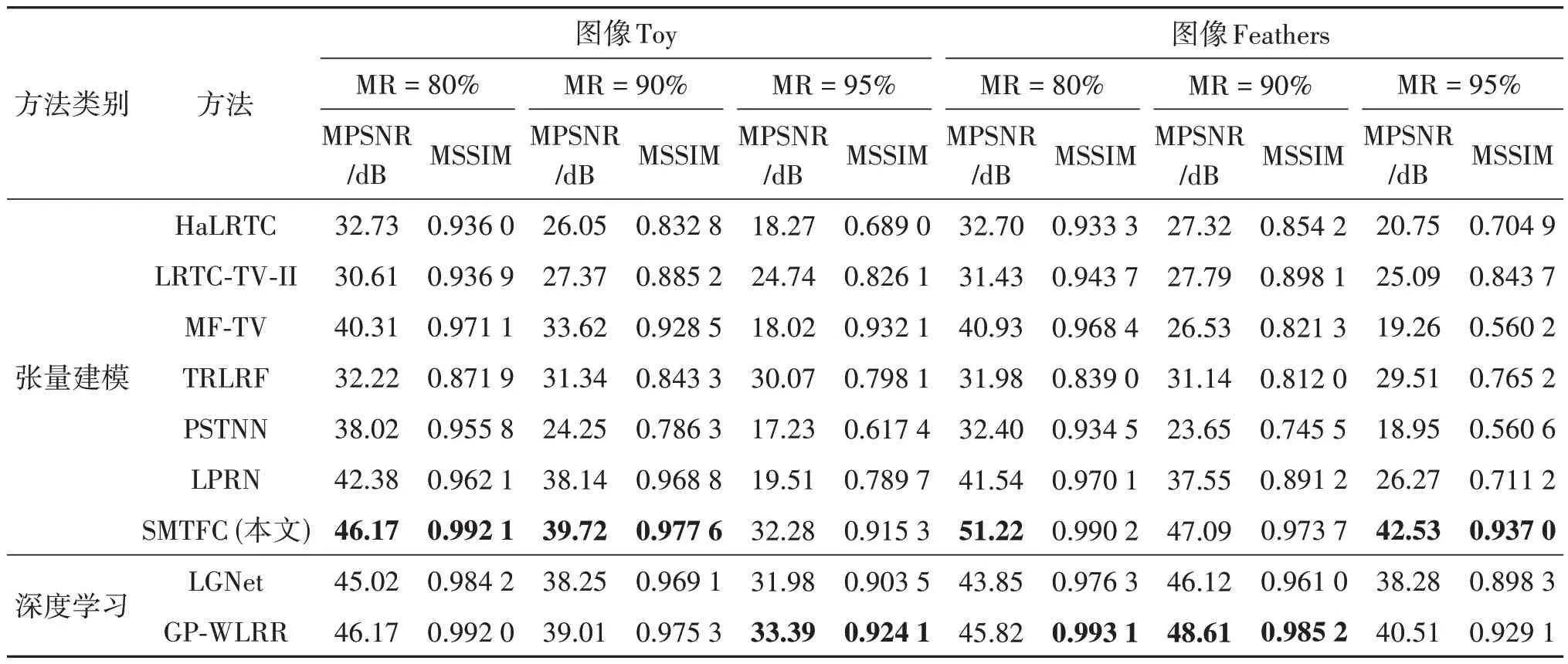
表2 不同恢复方法在多光谱图像上的定量比较Table 2 Quantitative comparison of different completion methods for MSI
在主观视觉效果方面,图9 和图10 显示了在丢失率为90%的情况下,不同方法在图像Toy和Feathers 第30 光谱波段的恢复结果。以Feathers 图像为例,提出的SMTFC 模型的PSNR 值最高,并且在较高数据丢失率下,该模型仍能有效恢复羽毛的边缘细节以及精细纹理结构,其他方法无法恢复图像的纹理结构和边缘信息。因此,提出的SMTFC 方法可以有效保留图像的边缘结构与精细纹理结构,在恢复多光谱图像方面优于其他方法。

图9 不同恢复方法在多光谱图像Toy上的视觉评价Fig.9 Visual evaluation of different completion methods on Toy of MSI
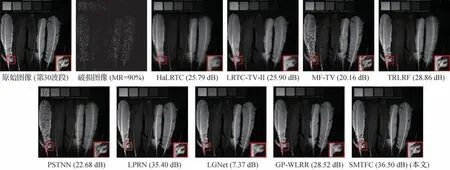
图10 不同恢复方法在多光谱图像Feathers上的视觉评价Fig.10 Visual evaluation of different completion methods on Feathers of MSI
5.3 视频
测试数据为YUV 视频,以Akyio 和Suzie 为例,测试数据尺寸为144×176×150。将每个视频数据进行归一化处理,MR同样设置为80%、90%和95%。图11 为本次实验视频数据集,其中图11(a)(b)分别为Akyio和Suzie视频数据的第1帧。

图11 YUV视频图像数据集Fig.11 YUV video datasets((a)Akyio;(b)Suzie)
表3为在丢失率为80%、90%、95%时,不同方法在Akyio 以及Suzie 视频数据集上恢复张量的MPSNR、MSSIM 值。在所有实验方法中,对于不同丢失率的视频图像,提出的SMTFC 模型在Akyio、Suzie数据集上获得了最佳的恢复精度。
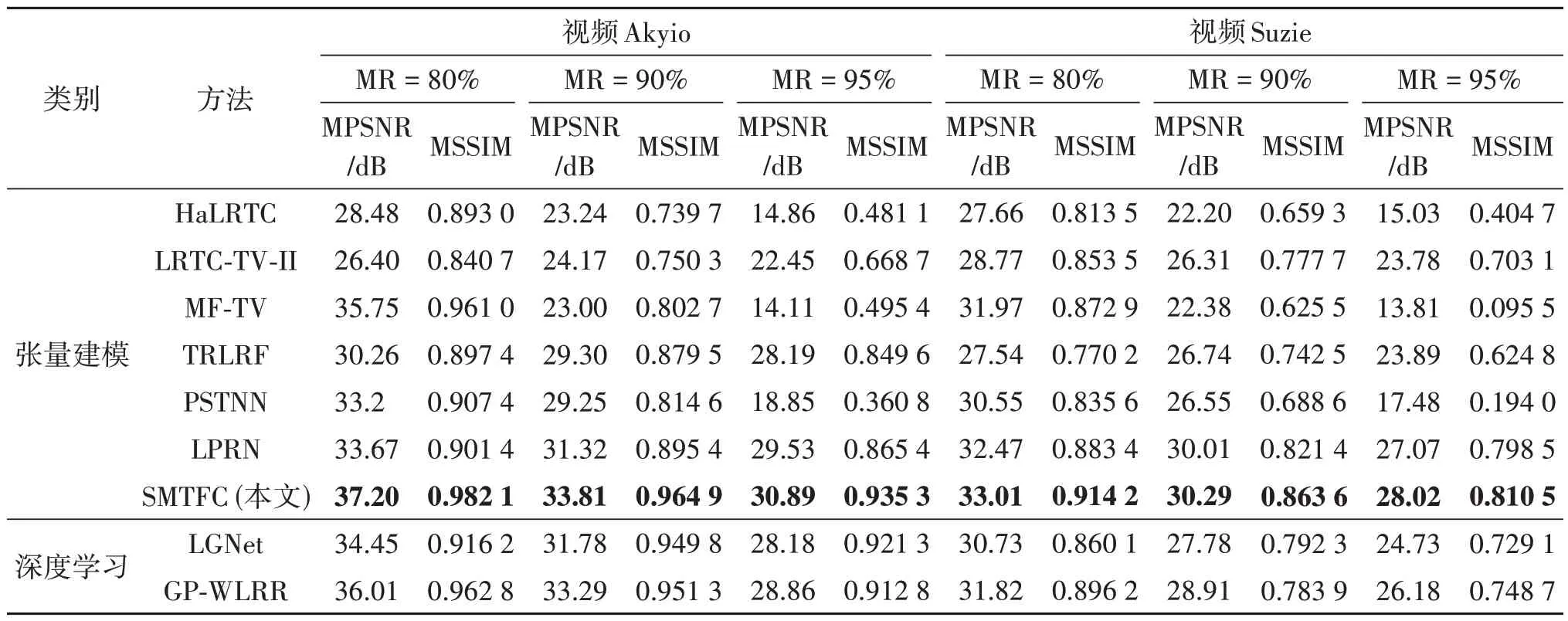
表3 不同恢复方法在视频数据集上的定量比较Table 3 Quantitative comparison of different completion methods for video datasets
在视觉评价方面,图12 和图13 显示了在MR 为90%的情况下,不同恢复方法修复Akyio 和Suzie 视频数据的第10帧图像。可以看出,提出的SMTFC模型PSNR 值最高,有效保留了视频中精细的纹理结构与边缘细节,获得了良好的视觉效果。综上所述,SMTFC 模型在恢复视频图像数据上优于其他方法。

图12 不同恢复方法在视频数据Akyio上的视觉评价Fig.12 Visual evaluation of different completion methods on Akyio of video datasets

图13 不同恢复方法在视频数据Suzie上的视觉评价Fig.13 Visual evaluation of different completion methods on Suzie of video datasets
5.4 医学图像
本小节测试图像模拟了正常大脑的磁共振成像,数据集大小为181×217×181,数据中每个像素的大小均在0至1之间。
在客观指标方面,表4 为在丢失率为80%、90%和95%时,不同恢复方法在医学图像数据集上的定量比较。在所有实验方法中,对于不同丢失率的医学影像图像,SMTFC 模型获得了最佳的恢复精度。在统计意义上,SMTFC 获得最佳的恢复性能。综上所述,提出的SMTFC 模型在恢复医学图像数据上优于其他方法。
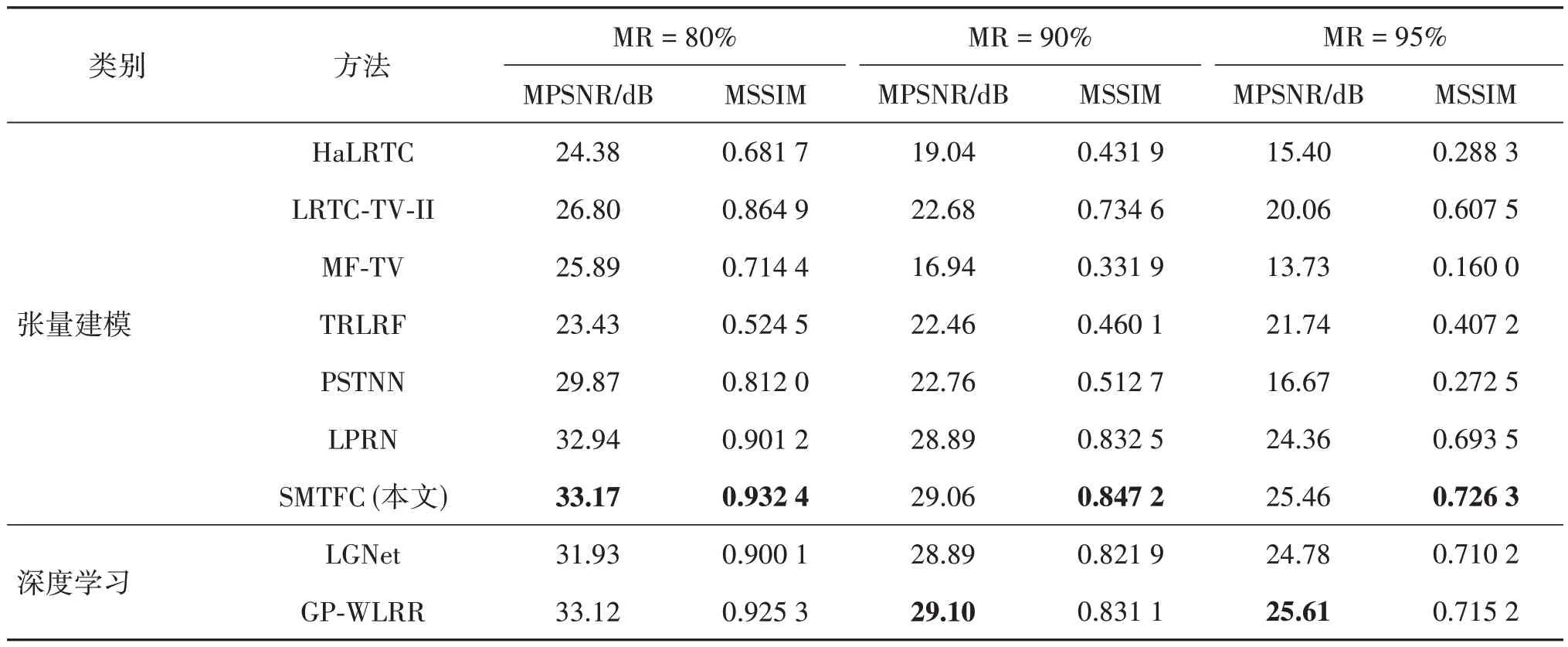
表4 不同恢复方法在医学图像数据集上的定量比较Table 4 Quantitative comparison of different completion methods for medical images datasets
图14 显示了在丢失率为90%的情况下,不同恢复方法恢复医学图像数据的第10 个切片。如图14所示,提出的SMTFC 模型恢复图像的PSNR 值最高,LRTC-3DTV 模型恢复图像的PSNR 值次高。SMTFC模型恢复的图像主观视觉效果最佳,而其他的实验方法在高丢失率的情况下无法有效恢复医学图像的精细的纹理信息与边缘结构。
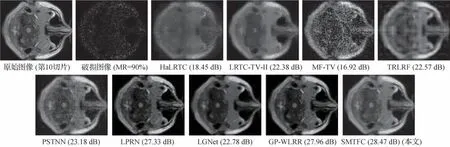
图14 不同恢复方法在医学图像数据集上的视觉评价Fig.14 Visual evaluation of different completion methods for medical images datasets
另外,表5 进一步给出了SMTFC 和GP-WLRR在某些方面的对比结果。其中,GP-WLRR方法使用PyTorch 1.13.1 框架,开发环境为PyCharm Community Edition 2021.1.3,本文SMTFC 方法运行环境为MATLAB R2021b,不需要进行神经网络预训练,经过算法迭代即可得出结果。GP-WLRR 模型采用49.39 M 大小的数据集进行预训练之后,还需要使用200 个张量数据进行针对本任务的参数微调,而本文方法不必进行微调。当MR 为95%时,本文方法在4 种不同数据集上达到最高MSSIM 的情况下,修复一个多维张量数据所需平均时间为310.83 s,GP-WLRR 为789.75 s。因为运行环境不同无法严格进行时间比对,但从一般意义上来说,本文方法平均所需时间远少于GP-WLRR。

表5 本文方法与GP-WLRR比较Table 5 Comparison between SMTFC and GP-WLRR
6 结论
在传统方法中,全变分施加于整体张量数据,无法探索张量低维子空间的平滑先验,并且传统张量分解诱导的张量秩无法灵活处理不同模式下的相关性,导致张量恢复模型缺乏稳定性。本文提出了一种基于稀疏先验与多模式张量分解的低秩张量恢复算法,能够处理张量数据不同模式之间的相关性和张量子空间稀疏性。具体而言,在对原始张量施加核范数约束,恢复张量全局低秩性的同时,利用张量多模式分解将原始张量沿着每个模式方向分解为一个低维张量和一个因子矩阵,以便处理不同模式下的相关性,增加模型的稳定性。其次,因子梯度稀疏正则化约束可以有效处理张量子空间稀疏性,也可为模型提供更多的辅助信息。将本文方法与8 种张量恢复方法在高光谱图像、多光谱图像以及医学影像图像上进行对比实验,本文模型在4 种张量数据相比于传统方法及LGNet 均获得了最佳的实验结果,与深度学习方法GP-WLRR 的实验效果基本持平。本文模型可同时利用张量的全局低秩性与局部稀疏性,能够对不完整张量数据进行修复。本文模型对整体张量施加了张量核范数约束,可以有效利用张量的全局低秩性,然而,在优化求解时,会使用到大量的张量奇异值分解操作,导致模型收敛速度减慢。在未来工作中,将考虑使用更加高效的张量秩函数,减少张量奇异值分解次数。

