联合深度学习和宽度学习的纹理样图自动提取

吴惠思，梁崇鑫，颜威，文振焜

深圳大学计算机与软件学院，深圳 518060

0 引言

纹理合成（Wei等，2009；王相海和陶兢喆，2013）是利用其结构内容从小数字样本图像通过算法构造大数字图像的过程。它是计算机图形学的研究对象，并用于许多领域，包括数字图像编辑、3D 计算机图形学和电影后期制作。作为一种有效的方法，基于样图的纹理合成（朱文浩和魏宝刚，2008；Zhou等，2018）旨在从输入样图中创建新的纹理图像，这些图像在视觉上与输入相似，但不是它的简单副本。纹理过程可以分为3 个部分（Wei 等，2009）：纹理获取、纹理映射和纹理渲染，其中包括如访问、采样和过滤等多种问题。本文重点介绍纹理样图的获取过程，即纹理样图提取。

当前存在多种方法获取源纹理样图，例如手绘图像或扫描照片，但这些方法获取的纹理过程耗时耗力且获取的纹理种类是十分局限的。互联网可以提供种类繁多的图像素材，因此设计自动地从这些图像中提取高质量纹理样图的方法是十分有意义的。然而，当前关于纹理样图提取的工作很少，而输入纹理样图的质量很大程度上可以决定最终合成结果的效果。此外，获取纹理样图仍然是一项劳动密集型任务，通常需要仔细拍摄、手动裁剪和后期处理。因此，如何简单有效地从给定图像中提取所需的纹理样图成为一个新颖且具有挑战性的问题。本文旨在利用纹理特征提取出有效的纹理样图用于下游任务（如纹理合成任务）。纹理特征提取具有以下任务特点：多样性、不变性、稳健性和实时性。深度学习在机器学习领域掀起了一股研究浪潮，凭借其出色的性能，深度学习在模式识别、图像识别、语音识别和视频处理等领域的应用越来越多。Trimmed T-CNN（texture convolutional neural network）（Wu 等，2021）被提出且应用到纹理样图提取任务中，并取得了不错的纹理样图提取效果，该方法结合了选择性搜索算法和卷积神经网络。然而，选择性搜索算法在生成候选区域时十分耗时，并且用深度学习网络进行纹理样图分类也存在耗时的问题，因此无法满足特定场景下实时性的需求。此外，深度学习网络中涉及大量的中间参数、复杂的结构以及超参数等因素，这使得深度学习网络的训练和更新变得复杂且耗时。不同于深度学习，宽度学习系统致力于神经网络的宽度延展而非深度延展来解决复杂问题，这可以有效克服深度学习训练过程耗时长的缺点，其通过快速增量来构建网络模型。因此，本文引入宽度学习系统来进行纹理样图的识别与分类，用于提升提取纹理样图的速度。由于其没有多层连接，并且宽度学习也不需要使用梯度下降来更新权重，因此计算速度比深度学习要快得多。

与传统的基于特征的纹理样图提取方法不同，本文方法是一种基于学习的方法，结合了深度学习和宽度学习的优点。具体来说，采用残差特征金字塔网络用于提取特征图而不是手工制作的特征。然后提出使用区域候选网络来获得潜在的理想纹理样图候选区域。最后，将这些候选区域输入宽度学习系统进行分类，并利用评分和排名算法以获得最终结果。

本文的主要贡献如下：1）使用深度学习方法来提取纹理样图的候选区域。本文改进了区域候选网络，使其比以前的检测方法更适合提取理想的纹理样图；2）首先将宽度学习系统应用于纹理分类，设计的网络结构和增量学习算法可以准确快速地区分不同类型的纹理；3）充分结合了深度学习和宽度学习的优点，利用深度学习从原始图像中提取丰富的纹理特征，将提取的特征通过宽度学习进行分类。

1 纹理样图的自动提取

提出算法的整体框架如图1 所示。给定输入图像，通过特征金字塔网络提取纹理特征，并根据输入图像的尺寸选择特定的一层作为特征图。此特征图是整个图像的特征图，为所有候选区域共享，不需要为每个候选区域分别提取特征。然后将该特征图输入到轻量的区域候选网络中生成纹理候选区域。注意，此时产生的候选区域是类别无关的，即可以认定哪些是前景哪些是背景，但是不确定具体是哪一类的纹理结构。下一步结合纹理特征图和候选框，通过宽度学习对这些区域进行分类。最后，在基于块大小和分类精度的细化步骤中，使用评分和排序策略识别最佳纹理样图。

图1 联合深度学习和宽度学习的纹理样图自动提取的整体框架图Fig.1 Overall framework of automatic texture exemplar extraction with jointed deep and broad learning models

1.1 基于金字塔的特征提取器

使用ResNet（residual network）（He 等，2016）作为主干网，其是一个用于特征提取器的标准卷积神经网络，其中浅层的卷积核检测低级特征（空间信息），深层的卷积核检测高级特征（丰富的语义信息）。通过主干网络，将一幅1 024 × 1 024 × 3 的RGB 彩色自然图像转换为32 × 32 × 2 048 的特征图。特征金字塔网络（feature pyramid network，FPN）（Lin 等，2017）通过添加第2 个金字塔，改进了标准的特征提取金字塔到较低的层，使得深层的图像特征可以融合到浅层当中。通过这种做法，允许每个级别的层次同时访问到较低级别和较高级别的特征。这样的架构通过自顶向下的路径和横向连接，将低分辨率、语义强的特征与高分辨率、语义弱的特征结合起来，从而得到一个在所有层次上都具有丰富语义的特征。并且，不同于以往靠不同尺度的输入图像来建立多尺度特征，这里仅仅需要一个尺度的输入图像即可，特征金字塔网络会自动融合不同尺度的特征。如图2 所示，两个金字塔之间存在横向连接，右侧的金字塔将深层的特征逐层融合到了浅层的特征中，根据输入图像的尺寸，可以选择合适的一层特征图进行下一步的预测。

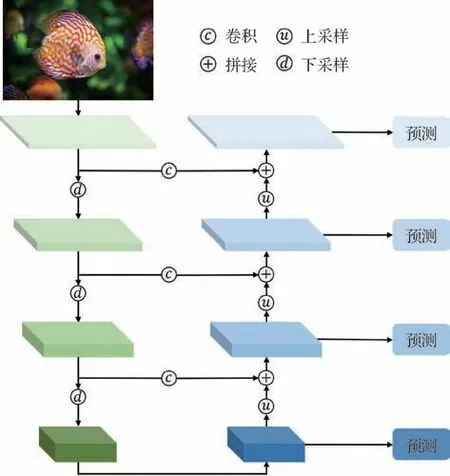
图2 特征金字塔网络结构示意图Fig.2 Schematic diagram of the feature pyramid network

1.2 区域候选网络

本文采用区域候选网络（region proposal network，RPN）（Ren等，2017）寻找潜在的纹理样图的候选区域，这是一个与类无关的、基于滑动窗口原理的目标检测网络。首先，基于前面步骤得到的融合特征图，设定卷积核的大小为3 × 3，得到一个新的特征图，这个操作的目的在于不改变长宽的情况下减少特征图的“厚度”。然后用1 × 1 的卷积核连接两个分支，分别执行区分前景和背景的二分类和边界回归任务。一般来说，核为1 × 1的卷积网络称为全卷积网络（fully convolutional network，FCN），用于逐像素运算，两层之间的特征图的长宽维度通常是相同的。因此，RPN 是一个用于寻找潜在候选区域的轻量级多分支神经网络。此外，该模型对输入图像的大小没有限制，即在不将维度缩放到固定大小的情况下，后续操作会将每个候选区域“切片”成均等的N×N个部分，每份取一个代表值，就得到固定的N的平方维度的向量用于后续分类。此外，在本文算法框架中，RPN与之前的特征提取完全是解耦的，并不限定特征提取方法，只要给出一个特征图即可。RPN网络的基本结构如图3所示。滑动窗口从特征图的左上角逐像素“滑动”到右下角，全面覆盖图像的每个区域。

图3 区域候选网络整体框架图Fig.3 The overall framework of the regional proposal network

对于特征图上的每个像素，以该像素为中心的目标对象的尺寸可能不同，因此需要设置一些长宽大小比例不同的预设框（又称为锚点框）。即对于同一个中心点，需要同时预测多个预设框的分数。每个中心点的预设框个数为k，如图3所示。每个预设框可以计算前景和背景的两个分数以及中心点坐标加预设框长宽4 个位置信息，所以总共可以获得2k个分数和4k个坐标信息。通常设置9个不同尺寸的预设框，即k=9，包括3 种不同的尺寸和3 种不同的长宽比例。这样做的好处是，无论纹理基元如何缩放，总有一个合适的预设框与之匹配。如图3 所示，首先从特征图选取3 对大小不等的正方形（小、中、大等比例的实线框），作为候选纹理块的预设框。在训练RPN 时，对每个预设框都要进行二分类（前景或背景）。本文利用预设框与ground truth（真实框）之间的交并比（intersection over union，IoU）来为预设框分配类别标签（前景或背景）。在本文中，定义分配准则如下：1）如果预设框与对于给定的真实框之间具有最高的IoU 或与任何真实框之间的IoU超过0.7，则为该锚点框分配正标签，即前景；2）如果预设框对于所有真实框的IoU 低于0.3，则为锚点框分配负标签，即背景；3）未被分配标签的预设框不参与训练。然后，选择最可能包含目标的预设框并优化它们的位置和大小。注意，如果几个预设框重叠太多，本文使用非极大值抑制（non-max suppression，NMS）（Neubeck 和van Gool，2006）进行筛选，即保留前景得分最高的一个并丢弃其余的。最后，将生成的最终候选区域传递到下一阶段。RPN的损失函数定义为

式中，i代表预设框的索引，pi代表预设框预测为前景的置信度，ti表示预设框的4 个坐标信息向量。表示ground truth 标签，如果预设框被识别为前景，则为1；如果识别为背景，则为0。表示关联的真实框的前景坐标信息向量。分类损失Lcls基于二分类的对数损失函数。对于坐标信息的回归损失Lreg，其中考虑了为1 的情况，毕竟只有前景才能有与之相关联的真实框。这两个损失函数分别由Ncls和Nreg归一化，并且两者的权重由λ平衡。

1.3 宽度学习

尽管深度神经网络的结构性能优异，但由于涉及大量中间参数、复杂的结构和超参数等因素，训练阶段是一个耗时的操作。如果没有达到目标的准确性，则需要从头开始重新训练。深度学习模型由于可以拟合多种函数曲线，无限逼近训练数据的分布情况，常常用于有监督的分类和回归任务。在训练阶段，其采用梯度下降算法更新权重参数，学习率等超参数的设置对其泛化性能影响较大。因此，它们往往存在收敛慢以及陷入局部极小值的问题。另外，由于深度学习网络模型的复杂性，参数量通常在百万级别以上，使得从理论上分析深度学习网络结构参数之间的关系并不可行，所以凭借经验，为了让网络模型更准确，大多数情况下需要微调参数，添加更多层或改变层的结构。

宽度学习（Chen 和Liu，2018）提供了另一种新思路，它是一种没有深度结构的神经网络，训练阶段具有快速和准确的特点。宽度学习基于随机向量功能链接神经网络（random vector function links neural networks，RVFLNN）（Pao 和Takefuji，1992；Pao 等，1994；Igelnik 和Pao，1995），可以看做是一个扁平的网络，将原始输入数据作为特征节点，横向扩展结构。如果网络结构需要扩展，其中包括输入数据、特征节点和增强节点的扩展。使用增量学习算法快速更新参数，而无需从头开始训练。宽度学习采用增量学习的方法，在不叠加层结构的情况下，横向扩展神经网络节点并增量更新权重。在本文算法中，宽度学习可以概括为以下过程：可以将上一步获得的候选区域压缩为一维特征向量，将此当做特征节点，但是只有这些特征节点是不够的，还需要通过随机初始化的权重矩阵将原始特征扩充为增强节点，然后将所有的增强节点与原始特征节点拼接后通过权重矩阵连接到输出节点。其中，连接权重是通过伪逆和岭回归算法得到的。如果未达到所需的精度，则通过增量学习算法更新权重参数。宽度学习分类器的预测过程为：将从纹理提取步骤所得到的候选区域输入到宽度学习分类器中，然后由学习好的分类器为每个候选区域预测类别，最终输出分类概率。

1.3.1 动态逐步更新算法

对于常见的分类任务，A用于表示扩展的输入矩阵 [X|ξ(XWh+βh)]，它是输入向量X和增强向量ξ(XWh+βh)的组合。RVFLNN 提出了动态版本模型，对于额外新增加的输入节点或增强节点，可以快速更新模型的权重。不需要重新训练，而是在原来的基础上进行更新。现在，用A来表示n×m的矩阵，如图4 中的方框部分所示。本文引入动态逐步更新算法用于在网络中增加新的增强节点后快速更新参数，相当于向输入矩阵An添加一个新列a，表示为An+1=[An|a]。其中，新矩阵An+1的伪逆（pseudo inverse）由伪逆和a表示，具体为

图4 动态逐步更新算法Fig.4 Dynamic stepwise updating algorithm

式中，c=a-And。因此，可以得到更新后的权重参数为

式中，Yn是原始训练数据的预测值。由此可见，Wn+1的影响因素在于新增的a向量，通过一次计算a-And或An的伪逆，然后将其代入相应的位置就可以直接计算出新的权重参数。当c=0，即An是满秩矩阵时，伪逆和权重的计算复杂度更小。

宽度学习模型是在RVFLNN的基础上发展而来的。不同的是，宽度学习模型用输入向量形成特征向量，并提出以增量的方式更新模型的权重来适应新的数据。相比之下，以前的方法是直接使用输入向量来建立增强节点。现假设输入向量为X，用Zi=φi(XWei+βei)来映射输入向量，称之为第i组映射特征，其中Wei是随机初始化权重，与输入数据X相乘后得到输出Y。Zi≡[Z1，…，Zi]表示前i组所有映射向量的拼接。同样地，第j组的增强特征用Hj=ξj(ZiWhj+βhj)来表示，其中Hj≡[H1，…，Hj]表示前j组所有增强向量的拼接。这里的i和j属于经验值，根据问题的复杂程度和模型的准确性而定。而且，对于不同的i或k，φi和φk可以为不同的函数，以获得不同的非线性表示。同样，对于不同的j或r，ξj和ξr也可以为不同的函数。

现假设输入数据为矩阵X∈RN×M，输出向量Y∈RN×C，如图5所示。假设网络由n组特征映射构造，每组添加k个节点，则特征映射的方程可以表示为

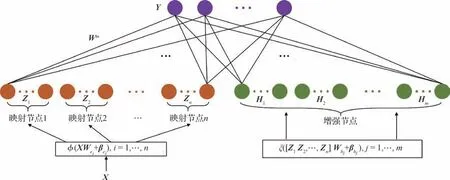
图5 宽度学习结构Fig.5 The diagram of broad learning system

式中，XWei和βei是随机初始化的权重参数。Zn≡[Z1，…，Zn]用于表示前n组的特征向量的拼接，第m组的增强向量则表示为

因此，宽度学习模型可以表示为

式中，Wm=[Zn|Hm]+Y是宽度模型从训练数据中学习到的权重参数，[Zn|Hm]+可通过岭回归近似计算出来。映射特征向量和增强特征向量的排列方式见图5。

1.3.2 宽度扩展的增量学习

在宽度学习分类器中，如果分类器无法达到预期的效果或训练类别增加，那么需要更加复杂的分类系统来解决，此时一种解决方案就是插入额外的增强节点以获得更好的性能，因此，引入宽度扩展的增量学习是非常必要的。宽度扩展的增量学习可以通过添加新的增强节点，提高分类器的灵活性和效率，使分类器系统能够更好地适应实际应用中的需求。下面详细说明增加p组增强节点的扩展方法，其中，矩阵Am=[Zn|Hm]，则Am+1可表示为

式中，Whm+1∈Rnk×p，βhm+1∈Rp。从映射特征向量到p组额外增强特征向量的连接权重和偏差是随机生成的。根据前面的讨论，可以推导出新矩阵的伪逆矩阵(Am+1)+为

式中，D=(Am)+ξ(ZnWhm+1+βhm+1)，

式中，C=ξ(ZnWhm+1+βhm+1)-AmD，则新的权重矩阵为

算法1 列出了宽度学习模型的学习过程，并且其结构如图5 所示，所涉及矩阵的所有伪逆运算都是用前述的正则化方法计算的。一般情况下，该算法只需要计算附加增强特征节点的伪逆，而不需要计算整个增强特征节点，因此可实现快速的增量学习。

1.4 筛选与排序

由于提取的图像块可能包含相似的区域和不同的尺度，因此本文需要评估所提取的图像块的质量。当前图像质量评估算法主要分为主观评价法和客观评价法。主观评价法受主观驱动，无法实现自动评估，故在此不赘述。客观评价法主要包括：峰值信噪比（peak signal-to-noise ratio，PSNR），结构相似性（structural similarity index，SSIM），特征相似性（feature similarity index，FSIM）以及自然图像质量评估（natural image quality evaluator，NIQE）等。PSNR 通过计算重构图像与原始图像之间的峰值信噪比进行评估，SSIM 是一种基于结构相似性的图像质量评估方法，FSIM 是一种基于特征相似性的图像质量评估方法，而NIQE则是一种基于自然图像统计特征的图像质量评估方法。在本文中，目标是从一幅输入图像中提取出理想的纹理样图，因此输出结果本就属于原图像的一部分，因此直接采用以上的这些图像质量评估的算法无法满足本文需求，故本文设计了一种纹理样图评分和排序算法，以获得最佳纹理样图并过滤掉不良样图。注意：本文设计的评分和排名算法不参与训练过程。

给定一幅自然图像I∈RH×W，其中H和W是图像的高度和宽度。首先通过RPN 获取一系列矩形候选区域Ri(x，y，w，h)，0≤i≤n且x，y，w，h分别是Ri的左上顶点的横坐标、纵坐标、候选框的长和宽。本文定义纹理样图的评分标准为

式中，Pi为分类器所得的分类准确率，Di代表候选区域与周围区域的分布特性，Si表示候选区域与输入图像尺寸的关系。a1，a2，a3是3 个特征的比例，且a1+a2+a3=1。在本文实验中，将a1，a2，a3分别设置为0.6，0.2，0.2。每个特征都从0归一化到1。其中，概率因子Pi为

式（13）表示输出层中第k类的最佳概率（0≤Pi≤1）。其次，矩形分布因子Di定义为

式中，C(x，y)是每个类别的（x，y）的平均值，本文将其表示为每个类别的中心点。d{C(x，y)，Ci(x，y)}为每个候选区域到均值坐标C(x，y)的欧几里得距离。dmax表示此类候选框中离均值点最远的距离。最后，本文定义相对矩形尺寸因子Si为

式中，Si为候选区域与原始输入图像的比值，wi，hi为第i个候选区域的长和宽，size(I)为原始输入图像的尺寸。由于尺寸较大的纹理样图可能包含更复杂的纹理特征，例如更复杂的光照分布或变形分布，因此本文将归一化尺寸添加到整体评分和排名中，将较大的样图排在较小的样图前面，并过滤掉图像尺寸太小的样图。另外，在实验中，将a1的权重设置大于a2和a3，因为本文认为分类模型的输出概率仍然是获得最佳纹理样图的决定因素。因此，基于上述评分和排序方案，本文算法框架仍然可以得到一组具有多种不同类型主导纹理内容的最佳纹理样图。

2 实验与分析

2.1 标准样图数据集

为了学习理想纹理样图的特征，重要的是要收集一个纹理数据集，其中包含所需纹理样图的可区分的和代表性的特征。目前，存在多个为纹理分类收集的开放纹理数据集。但其中大部分用于纹理识别基准数据集，例如DTD（describable textures dataset）数据集（Cimpoi 等，2014）、UMD（University of Maryland）数据集（Xu 等，2009）和UIUC（University of Illinois at Urbana-Champaign）数据集（Lazebnik 等，2005）。此外，也有几个用于材料识别基准的材料数据集，包括Kylberg 数据集（Kylberg，2011）、KTHTIPS（textures under varying illumination，pose and scale）数据集（Hayman 等，2004）、KTH-TIPS2 数据集（Caputo 等，2005）和FMD（Flickr material database）数据集（Sharan 等，2009）。然而，其中的大多数并不是为提取理想的纹理样图而设计的。

由于学习所需纹理样图的材料种类太多，无法详尽地收集，因此本文首先收集大量理想纹理样图并将它们分成若干类，每个类别都包含理想样图的通用代表性期望特征。在本文实验中，首先邀请艺术家从互联网上手动裁剪出数千个理想纹理样图，并将其作为标准纹理样图数据集进行后续分类和识别。为了学习纹理样图的固有特征，本文没有根据材料或标注的特征划分收集的数据集。相反，本文根据纹理块的尺寸和整齐度将标准数据集划分为6 类。使用S1、S2和S3分别表示具有小、中或大尺度对象的纹理样图。另外，使用R1和R2来表示具有随机或规则分布的纹理样图。因此，本文设计了6 类具有不同尺度和规律的理想纹理样本，包括S1R1、S1R2、S2R1、S2R2、S3R1和S3R2。典型样图示例如图6所示。

图6 典型的分类样图示例Fig.6 Tpical examples of classification exemplar

在本文的标准样图数据集中，首先从艺术家裁剪的图像中选择了1 260个最佳纹理样图，其中每个类别包含 210个样本。由于自然图像中的纹理块可能存在不同的光照和旋转，因此本文随机生成2 种不同的光照对比和4 种不同的旋转以生成更多的样本用于模型训练。最后，本文的标准纹理样图数据集包括10 080（1 260×8）个最佳纹理样图，每个类别包含1 680个具有不同照明和旋转的样本。

2.2 纹理样图提取

本文实验使用Python3和PyTorch实现了所提出的自动纹理样图提取模型。该模型使用NVIDIARTX 2080Ti GPU 进行训练，采用数据并行同步SGD（stochastic gradient descent）并设置minibatch为16幅图像。在实验中，本文算法中特征金字塔网络和区域候选网络的初始权重是通过ImageNet数据集预训练所得，然后通过收集的基于纹理基元结构的数据集进行训练。本文算法是基于目标检测的纹理样图的提取算法，因此数据集的标记方式类似于MS COCO（Microsoft common objects in context）数据集。在标记文件中，包含图像信息和标注信息，其中标注信息包含图像ID（identity），bbox 以及类别信息，数据集的标注说明如图7 所示。在实验中，使用数百幅自然图像来评估样图提取的精度和有效性能。宽度学习网络总共由10×10 个特征节点和1×11 000 个增强节点构成。具体来说，网络初始设置为具有10×6 个特征节点和7 000 个增强节点。

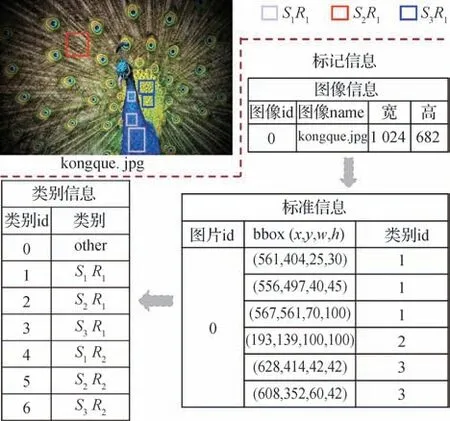
图7 数据集的标记方式示意图Fig.7 Schematic diagram of the labeling method of the dataset

然后，在每个步骤中，将10个特征节点和 1 000个增强节点插入到网络中。同时，在本文实验中，特征节点的映射函数（式（5））φ为线性函数，即利用W和β对X进行加权求和。其中，相关参数Wei和βei是从区间［-1，1］上的标准均匀分布中提取来进行初始化的。而增强节点中映射函数（式（6））ξ则采用sigmoid 函数，具体可表示为：ξ(x)=1/(1+ex)。为了测试所提出框架处理不同难度、不同类型的自然图像的能力，将收集的测试用例分为3 个级别。注意，为了方便排版，将所有可视化的纹理样图的尺寸调整为相同大小。

第1 类级别是简单的情况，表现为相当平稳的纹理基元排列方式，没有其他任何图像杂质或透视内容。典型示例如图8 平坦纹理样本。从结果图可以看出，本文方法即使在原始输入图像当中仅存在少量纹理基元结构的基础上也能成功提取到多种纹理基元大小的纹理样图。通常情况下，从图7 的示例中只能各提取一类纹理样图，即凉席或板栗，但是本文方法对于凉席可以提取S1R2、S2R2和S3R2这3 类不同的纹理样图，而对于板栗可以提取S1R1、S2R1和S3R1这3 类。从分数来看，都具有较高的分数值，分数越高纹理样图的质量越高。从这两个实验结果可以看出，本文所采用的提取算法能够有效地应对排列性质随机或规则的纹理基元结构。

图8 纹理样图提取的典型示例Fig.8 Typical examples of texture extraction in samples（（a）input images；（b）texture exemplar results）

第2 类级别是中等的情况，表现为多种纹理结构，有轻微的透视和非纹理结构，典型示例如图8 所示。从结果图可看出，本文的自动提取算法成功地提取了多个类别的纹理样本，即使在大象和鱼的部分包含轻微的透视和非纹理的区域。从大象图像提取到S1R1、S2R1和S3R1纹理样图类别，说明本文方法能够处理多种类别的纹理基元。另外，从鱼示例提取到的S1R2、S2R2和S3R2这3 类不同纹理基元大小的纹理样图，这说明本文方法能够较好地处理纹理基元结构和各种光照强度的图像。

第3 类级别是具有挑战性的情况，表现为具有严重的透视和变形，典型示例如图8 所示。通过结果可以观察到，本文方法仍然可以提取多个类别的质量纹理样图，即便在建筑或山脉当中含有较严重的干扰情况下。从建筑物（S2R1，S2R2，S3R2）、和山脉（S1R1，S2R1，S3R2）中提取的样图表明，本文方法可以输出任意排列性质和基元大小的纹理样图，而手工裁剪可能只裁剪一种类型的纹理样图，且很容易忽略其他类型的高质量纹理样图。

2.3 对比分析

为了评估本文网络的分类精度，本节采用了不同的卷积神经网络来实现理想纹理样图的分类，其中包括AlexNet（imageNet classification with deep convolutional neural network）（Krizhevsky 等，2017）、VGG-M（Visual Geometry Group）（Simonyan 和Zisserman，2015）、Deep-TEN（texture encoding network）（Zhang 等，2017）、FV-CNN（fusion view convolutional neural networks）（Cimpoi等，2015）、T-CNN（transposeconvolutional neural network ）（Andrearczyk 和Whelan，2016）、Trimmed T-CNN（Wu等，2021）、VGG-16（Ni 等，2022）以及BLS（broad learning system）（Chen 和Liu，2018）。在本文实验中，80%的纹理样本用于训练，剩下的20%用于测试。本文将纹理样图数据集分为简单、中等和困难3 个维度，一共进行了4组实验。

不同网络模型的比较如表1 所示，通过模型分类准确度进行比较，分类准确度指的是模型预测正确的样本数与总体样本的比值。分类的准确度方面，本文网络架构中的宽度学习分类器（BLS）总体上优于其他模型。尽管Deep-TEN 和FV-CNN 都是针对纹理分类而设计的，但它们更侧重于区分草地和建筑物之类的纹理。相比之下，Trimmed T-CNN和本文网络不区分纹理的材料属性，只是专注于提取6 种不同纹理基元和规律性的理想纹理样图。因此，Deep-TEN 和FV-CNN 通常具有更复杂、更深层次的架构，这对于本文中的实验来说是不必要的，由于它们不是专门为自动提取纹理样图而设计的，因此它们的性能不如本文方法。相比之下，Trimmed T-CNN的纹理特征网络的参数量仅为原始T-CNN的24%，与其他先进网络模型相比，参数权重量不超过10%。相较于Trimmed T-CNN，本文方法在参数量方面有所不足，但相较于其他对比方法，本文参数量显著减少，并且模型性能有所提升，且提取出的纹理样图更具多样性。

本文还对不同的纹理样图提取方法进行了用户调研。为了用户调研比较，选择了5 种先进的方法，包括Ni 等人（2022）、Trimmed T-CNN（Wu 等，2021）、Wu 等人（2018）、Dai 等人（2014）和Lockerman 等人（2015）的方法。本文的量化评估标准是邀请艺术家从给定的算法提取的样本纹理图中选择出满意的样图，并统计满意样图的数量。利用满意样图的数量与所有给定样图总量的比例作为提取质量的量化评估标准。在实验中，随机选择3组具有3个不同难度级别的自然图像，每组包括100 幅从这些图像当中提取到的纹理样图。

在2 组图像上运行了本文方法和对比方法，并得到每个竞争对手提取到的纹理样图。然后邀请艺术家选择满意的样图，并收集统计结果。典型示例如图9所示。

图9 本文方法与对比方法之间的结果比较Fig.9 Comparison between our method and competitors（（a）input images；（b）texture exemplar results）

将令人满意的样图数量绘制为测试图像总数的函数，如图10 所示。从3 种不同难度的图像数量来看，满意程度随着困难难度的增加而下降，而本文方法总体优于其他对比方法，能有效地根据纹理基元的大小和排列性质尽可能提取更多的高质量纹理样图。更重要的是，这5 种对比方法都是基于特征的方法，需要提取特定的图像特征或在纹理样图提取之前就预先定义纹理的初始位置。与这5 种对比方法不同的是，本文方法是基于学习的方法并且是全自动的，不需要任何用户输入来指定所需纹理的初始图像特征、位置以及比例。

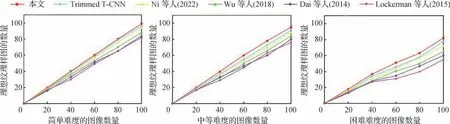
图10 理想纹理样图统计比较Fig.10 Statistical comparison of ideal texture samples

更进一步地，为了证明本文方法所提取到的纹理样图的质量，还将所提取到的纹理样图用于纹理合成任务，结果如图11 所示，通过该结果可以看出，合成后的图像在感知上与原纹理样图是等价的，这进一步说明本文提取纹理样图的有效性。

图11 纹理样图应用于纹理合成Fig.11 Texture exemplar applied to texture compositing（（a）input images；（b）texture exemplar extraction；（c）texture synthesis results）

此外，本文设置了评分标准（式（12））用于提取出理想的纹理样图，为了确定评分和排序的参数设置，进行不同权重设置实验，最终统计结果如表2 所示。实验结果表明，a1，a2，a3分别设置为 0.6，0.2，0.2时达到最佳性能。

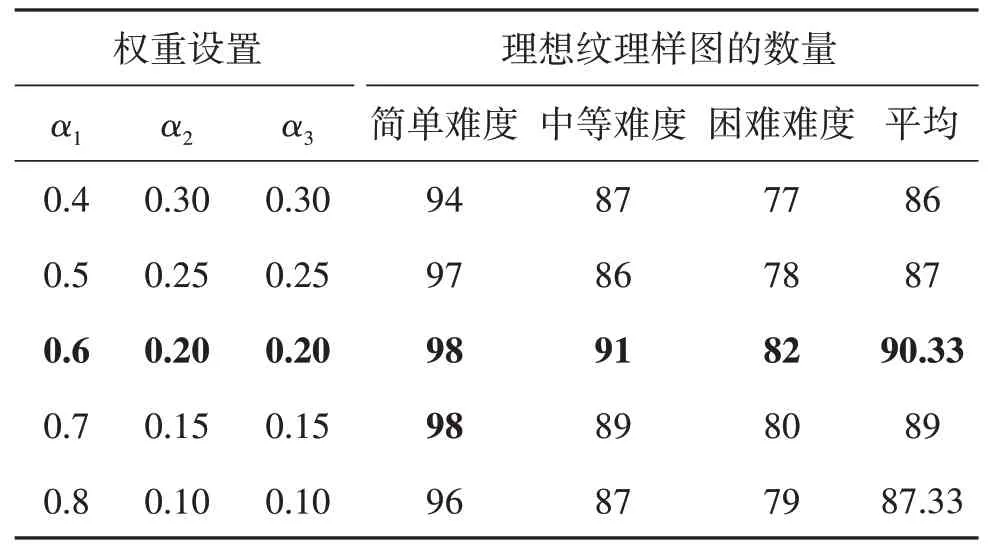
表2 评分标准中不同权重设置的性能比较Table 2 Performance comparison of different weight settings in scoring criteria

最后，还进行了时间统计分析。本文收集了许多具有不同分辨率的自然图像作为输入，它们被调整为3 种不同的尺寸，包括512×512 像素、1 024×1 024 像素和2 048×2 048 像素。为了最小化测试误差，本文重复了10 次计时统计，得出平均时间，结果如表3 所示。从结果可以看出，本文的时序统计主要包括自动纹理样图提取的3 个步骤，包括RPN、分类、评分和排序。此外，本文算法在速度方面要优于最先进的方法Trimmed T-CNN。具体来说，对于分辨率为512×512像素、1 024×1 024像素和2 048×2 048 像素的图像，本文算法的速度分别提高了1.393 8 s、1.864 3 s和2.368 7 s。

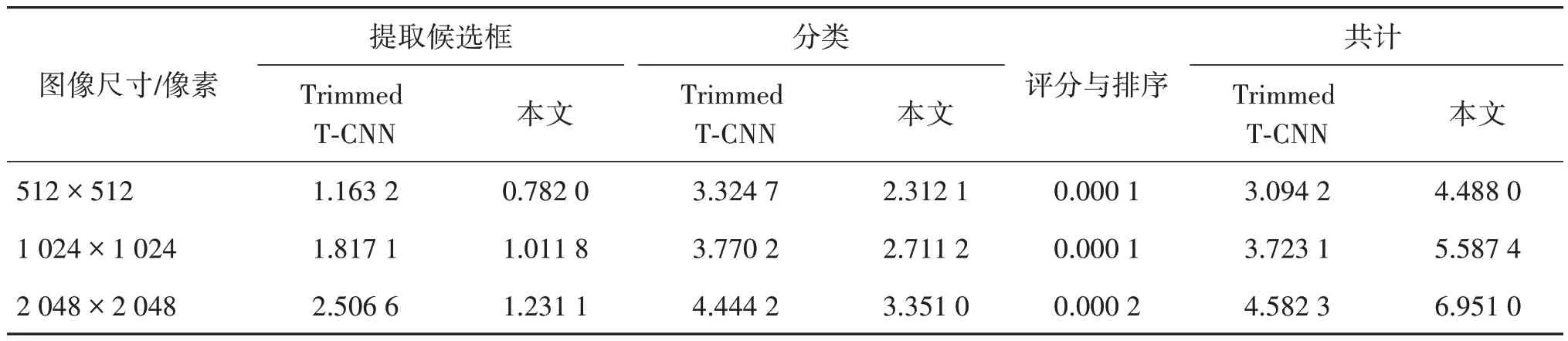
表3 本文方法对不同分辨率的输入图像的计时统计Table 3 Timing statistics of input images of different resolutions by our method/s

添加了更多的互联网图像纹理样图提取结果如图12 所示，该结果进一步展示了本文算法所提取出的纹理样图的有效性以及普适性。此外，本文算法仍存在一些需要改进的地方。首先，本文根据纹理块的尺寸和整齐度将标准数据集划分为6 类，但是纹理基元的不同大小和排列性质并不能完全覆盖自然图像的纹理样图，如图13 所示。因此，对于一些自然样图本文提出的算法不能提取出满意的纹理样图结果，若能进一步扩充纹理样图数据集，特征分析的效果和纹理样图的提取质量将会得到进一步提升。其次，对纹理样图结果的评分排序，可考虑更多的评价标准来降低人为的主观因素对纹理样图的评价的影响，例如考虑纹理样图的可合成性等。

图12 更多的纹理提取结果示例Fig.12 More examples of texture extraction results（（a）input images；（b）texture exemplar results）

图13 不属于标准数据集中6类纹理的其他类Fig.13 Other categories that do not belong to the six categories of textures in the standard dataset

3 结论

本文提出了一个基于宽度学习和区域候选网络的自动纹理样图提取算法，首次将宽度学习应用于自动纹理样图提取任务之中。为了学习高质量的纹理样图，设计了标准的理想样图数据集和基于CNN 的深度纹理样图提取方法，其中包含数千个所需的纹理样图。具体来说，ResNet FPN 主干网络和宽度学习用于纹理样图分类和识别的滤波器组。同时，进一步采用了改进的区域候选网络算法用于提取潜在的纹理样图块，其中所有候选者都被放入后续的宽度模型中，旨在有效地学习理想的纹理样图。最后，本文通过评分和排序策略获得最佳纹理样图。本文的纹理样图提取系统使用多种纹理进行评估，并且与最先进的深度CNN 架构进行了比较，得到的统计分析结果和用户调研结果都表明了本文方法的有效性。