基于有源阻尼控制的区域电网新能源基地次同步振荡抑制的研究

赵 鹏，黄云辉，王 栋，唐金锐，周克亮，肖厦颖

（1.武汉理工大学自动化学院，湖北武汉 430070；2.湖北省电力规划设计研究院有限公司，湖北武汉 430040）

0 引言

近年来，随着高比例新能源和高比例电力电子设备接入电力系统[1-2]，电网次同步振荡（Subsynchronous Oscillation，SSO）现象时有发生[3]。例如，2016 年南澳大利亚发生的9.28 大停电事故，2015年新疆哈密地区风电场发生过SSO 事件等[4-9]。

现今，许多学者已对可控串联补偿、构网型变流器、静止无功补偿器、储能设备等抑制措施展开了大量研究[10-18]，其中附加阻尼控制器（Sub-synchronous Damping Controller，SSDC）具有性价比高和抑制效果较好等优点，因而得到广泛的研究和应用。文献[19]提出了1 种基于虚拟同步发电机的附加阻尼方法，该方法能够在不降低频率稳定性的前提下提高功角稳定性。文献[20]提出了1 种改进的电容电流反馈有源阻尼控制方法来抑制系统振荡。但文献[19-20]并未对有源阻尼控制器的参数进行详细分析设计。文献[21]提出了直驱永磁同步风力发电机附加阻尼控制策略提升柔直送出稳定性，但文中并未分析阻尼形成的机理。文献[22]通过在双馈风机转子侧附加阻尼控制器能够有效为系统提供正阻尼，从而抑制系统次/超同步振荡。文献[23]通过在虚拟同步发电机VSG（Virtual Synchronous Generator，VSG）的有功环上附加阻尼控制器的方法来抑制系统低频振荡。文献[24]则在分布式潮流控制器输出电压控制环节上设计了1 种基于相位补偿的附加阻尼控制器。文献[25]提出了1 种基于风电系统功率控制回路附加阻尼控制以抑制系统低频振荡。但文献[22-25]最后都未基于实际的区域电网算例进行仿真分析，其阻尼控制策略抑制效果还有待于验证。

本文首先在Matlab/Simulink 仿真平台搭建某市区域电网模型，探究该地区由于新能源渗透率不断升高可能面临的次同步振荡问题；其次，提出基于有源阻尼控制的新能源基地次同步振荡抑制策略，通过采集电网侧频率，经过幅值校正环节和隔直环节，然后对振荡频段内的输出信号进行相位校正，从而改善系统阻尼特性，进而对有源阻尼控制器参数进行设计，并通过特征根分析法和Prony 算法进行验证；最后，基于该区域电网算例进行仿真分析，验证了本文所提出的有源阻尼控制策略对次同步振荡抑制的有效性和适用性。

1 大规模新能源接入区域电网的次同步振荡分析

1.1 某市区域电网现状

该地区位于淮河和长江两河流域的交汇之地，地形主要以平原和丘陵为主，水能资源有限，但风电、光伏资源较为充裕。随着社会经济和工业基础的飞速发展，能源需求量逐年增加，超前谋划能源电力增长点，大力发展新能源成为必然选择。

该地区近6 年新能源总装机容量如表1 所示。由表1 可知，该地区新能源总装机容量总体呈逐年上升趋势，同时新能源渗透率也不断提高。并且，自2017 年起该地区新能源渗透率已超过50%，属于典型的可再生能源中心。

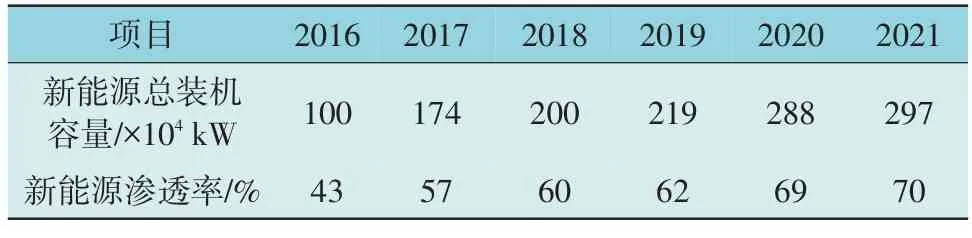
表1 某市2016—2021年新能源总装机容量Table 1 Total installed capacity of new energy in certain city from 2016 to 2021

截至2022 年底，该区域新能源装机总容量为3.017×106kW，各机组装机容量如图1 所示。根据当地电源建设规划和“十四五”能源规划，该地区新能源开发潜力较大，截至2025 年，该区域新能源总装机容量将达5.613×106kW，其中风电装机1.684×106kW，光伏装机1.86×106kW。

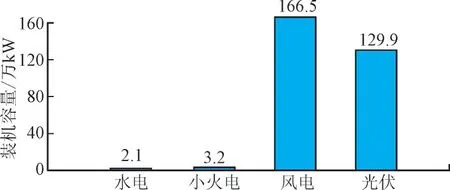
图1 2022年各机组装机容量Fig.1 Installed capacity of each unit in 2022

由于大规模新能源基地持续接入该区域电网，导致其渗透率不断提升，新能源并网运行失稳风险也将不断增大。传统可再生能源出力波动特征显著，并且不具备惯量控制和频率支撑能力，大规模新能源接入替代了传统的同步发电机，将会降低系统的转动惯量与电网强度，不利于电网的电压和频率稳定，因此，以新能源机组为代表的电力电子设备相互作用或与同步电机相互作用状态间可能会产生次同步振荡，进而导致新能源基地失稳而大规模切机。其中，电网强度可以用短路比SCR（Short Circuit Ratio，SCR）来衡量。

1.2 区域电网次同步振荡风险

本节采用Matlab/Simulink 建立了实际的该区域电网仿真算例，为便于建模仿真分析，对地理接线图进行简化等值，简化等值为31 节点的电网系统，某区域电网节点图如图2 所示。图2 中，G1和G2均为火电厂，G3至G10分别为对应节点的等效电厂。

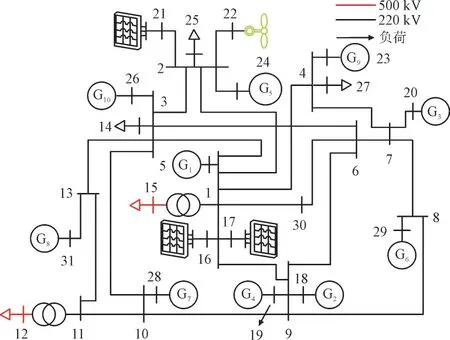
图2 某市220kV及以上电压等级区域电网节点图Fig.2 Node graph of regional power gird with voltage levels of 220kV and above in certain city

图2 该区域电网包含1 座150 MW 的风电场，2座容量均为600 MW 的光伏基地，1 座容量为120 MW的光伏基地，2 个容量为660 MW 的火电厂。

由于该地区区域电网秋季高负荷时段新能源出力较大，新能源渗透率高，对电网运行稳定性影响较大，因此，本文重点分析秋腰运行方式下新能源基地接入对该地区区域电网动态特性及运行稳定性的影响。在秋腰运行方式下，该地区的负荷为3 351 MW。本文以下仿真结果中的功率均为标幺值，基值为100 MW。

为方便观察功率小扰动时系统的稳定性情况，在仿真过程中，当系统稳定运行后，在6 s 时对节点21光伏基地有功指令值上施加+5%的功率扰动，对该地区线路传输功率情况进行仿真分析，仿真结果如图3所示。节点21 周边线路传输功率产生次同步振荡，整个系统将面临次同步振荡风险。同时，由Prony 算法分析得出系统此时在无阻尼控制时主导振荡模式的特征值为-7.81±24.19i，系统阻尼比为0.307 2。

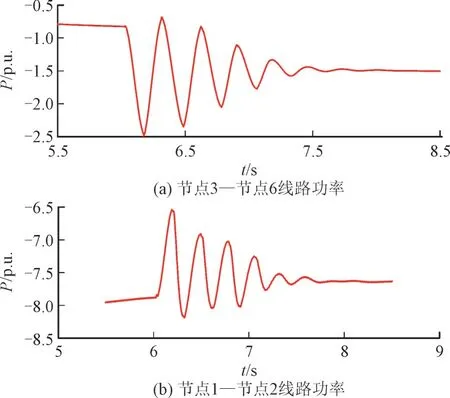
图3 系统稳态运行下节点21光伏基地光照强度突增时线路传输功率电磁暂态响应Fig.3 Electromagnetic transient response of transmission power during sudden increase of light intensity at node 21 photoroltaic base under steady state system operation

当新能源基地接入节点1 时，保持系统其他功率输入输出不变，将新能源基地的输出功率增大，一直到该区域电网失稳为止，对该地区线路传输功率电磁暂态响应情况进行仿真分析，结果如图4 所示。发现新能源基地的输出功率的稳定性极限在2 675 MW，经计算新能源基地并网点的短路比为1.45。当新能源基地输出功率超过2 675 MW 时，此时短路比小于1.45，系统会产生振荡失稳。同时，由Prony 算法分析得出此时系统在无阻尼控制时主导振荡模式的特征值为8.53±42.98i，系统阻尼比为-0.194 7。因此，随着该区域新能源大规模接入，新能源渗透率不断升高，使整个系统也将面临次同步振荡风险。

图4 节点16—节点17两个光伏基地容量之和超过稳定边界时线路传输功率电磁暂态响应Fig.4 Electromagnetic transient response of transmission power when the sum of two PV base capacities at node 16 and node 17 exceeds the stability boundary

2 基于有源阻尼控制的次同步振荡抑制方法

2.1 有源阻尼控制器基本结构

图5 为新能源基地的主电路及其控制策略图。其中，PCC 为公共并网点，PWM 为脉冲宽度调制，f为电网频率，θ为锁相角，ut为并网电压，ug为电网电压，Xf为滤波阻抗，Xg为电网阻抗，i为线路输出电流，id为电流内环控制d轴分量，iq为电流内环控制q轴分量。

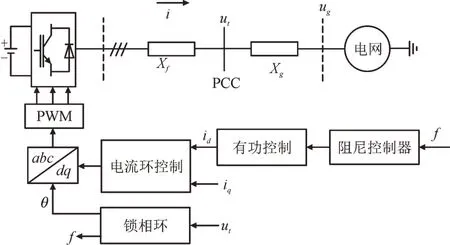
图5 新能源基地的主电路及其控制策略Fig.5 Main circuit of the new energy base and its control strategy

图6 为有源阻尼控制器基本结构框图，包含滤波环节、幅值校正、隔直环节、相位校正以及限幅5个环节。其中，dPref为功率补偿变化值，Pref为原有功控制参考指令值，为现有功控制参考指令值，P为新能源场站电磁输出功率，K为幅值校正参数，T为滤波器时间常数，T1和T2为相位校正参数，m为校正阶数，s为拉普拉斯算子。

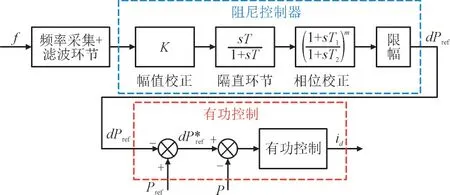
图6 有源阻尼控制器基本结构框图Fig.6 Basic structure block diagram of active damping controller

该阻尼控制器首先采集电网频率，经过幅值校正、隔直环节、相位校正以及限幅环节后得到功率补偿变化值；原有功控制参考指令值与功率补偿变化值作差得到现行有功控制参考指令值；最后通过控制光伏并网变流器有功功率环调节新能源场站输出功率。由于系统自身需要维持电网发电与负荷功率平衡，所以新能源场站输出功率变化会导致同步机输出功率变化，达到稳定电网频率的目的。

2.2 有源阻尼控制器参数设计

有源阻尼控制器的数学表达式如下：

有源阻尼控制器的参数整定主要包括幅值校正、隔值环节以及相位校正3 个环节相关参数。

幅值校正参数K直接影响阻尼控制器提供阻尼的强弱，幅值校正参数越大，阻尼效果越好。但幅值校正参数的选取需考虑：（1）新能源场站校正控制有功容量约束；（2）引入有源阻尼控制器后新能源场站自身稳定特性。

针对于幅值校正参数K 选取时约束条件（2），在Matlab/Simulink 中搭建了具有有源阻尼控制器的光伏并网小信号模型与时域模型。分析当SCR=2，4，8 时，随着幅值校正参数K值的变化与系统稳定性的变化所示K值合适的取值范围。

由图7 可知，当光伏并网变流器中加入有源阻尼控制器后，随着K值的增大，系统的稳定性逐渐减弱。考虑该地区实际电网情况，由于系统短路比较低，因此只分析SCR=2 时不同K值下光伏输出功率情况，如图8 所示。

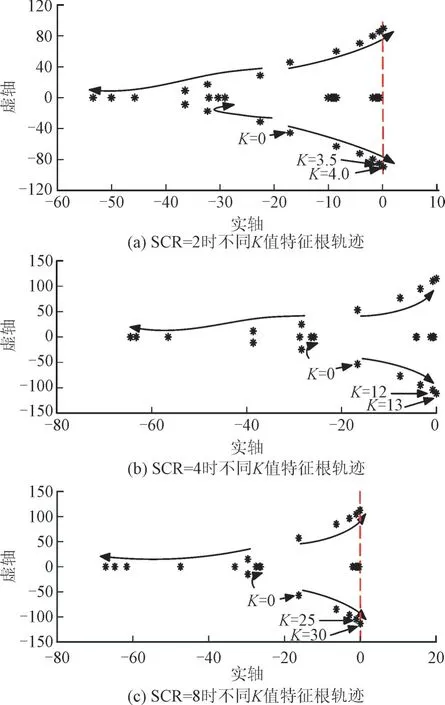
图7 当SCR=2，4，8时不同K值的系统特征根轨迹Fig.7 Characteristic root trajectories of the system with different values of K when SCR=2，4，8

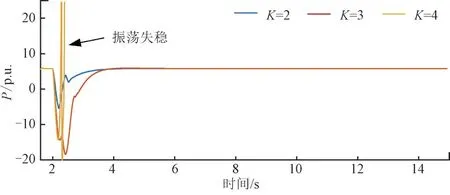
图8 当SCR=2时不同K值下光伏输出功率Fig.8 PV output power under different K values when SCR=2

发现时域仿真结果与特征值分析结果一致。所以，基于引入有源阻尼控制器后新能源场站自身稳定特性，综合考虑幅值校正参数建议取K∈[0，1]。

隔直环节的作用是使得阻尼控制器仅在发生振荡的动态过程中起作用。因此，要在保证直流信号能够充分衰减，且对振荡频段信号影响最小的前提下对滤波时间常数T值进行选取。综合考虑建议取T∈（0.5，1）。

相位校正环节作用是使阻尼控制器仅在发生振荡频段的输出信号进行相位移动，使得阻尼控制器能够为系统提供最大的正阻尼。相位校正环节各参数选取可参考经验公式，如式（2）所示。

式中：φ为相位校正环节的校正角，其取值为相位校正环节之前的有源阻尼控制器开环传递函数在振荡频率处产生的相移角度，建议当φ<30°时，m=1；当φ>30°时，m=2。

3 基于有源阻尼控制的区域电网次同步振荡抑制分析

为验证本文提出的有源阻尼控制策略的适用性和有效性，基于1.2 节对该区域电网的实际算例进行分析。新能源基地接入节点1，保持系统其他功率输入输出不变，当新能源基地的输出功率增大到2 600 MW 时，在11 s 时对新能源光伏基地有功指令值上施加+5%的功率扰动，取T=0.7，T1=0.08，T2=0.05，绘制无阻尼控制和不同幅值校正参数K的功率响应波形，如图9 所示。

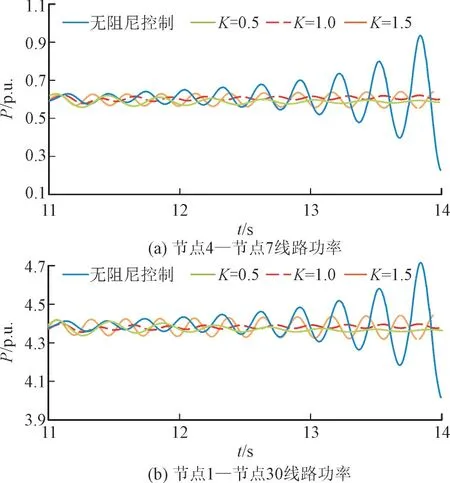
图9 无阻尼控制与不同K值下有源阻尼控制响应波形Fig.9 Undamped control and active damped control response waveforms with different K values

通过Prony 算法分析得出不同幅值校正参数K下系统的主导振荡模式特征值与阻尼比，其分析结果如表2 所示。可以发现，当K值从0.5 增加到1.5时，系统主导振荡模式阻尼比减小，系统稳定性变差。因此，随着幅值校正参数K的减小，附加有源阻尼控制器的新能源基地接入系统中的阻尼振荡抑制效果越好，且在实际工程应用中可根据保留一定稳定性裕量的需求调整幅值校正参数K的取值。

表2 不同K值下特征值与阻尼比分析Table 2 Analysis of eigenvalues and damping ratios with different values of K

4 结论

本文在保证新能源系统自身稳定性的前提下，提出了一种适合于新能源系统的有源阻尼控制策略，以抑制该区域电网由于新能源渗透率不断增大导致的次同步振荡问题。在实际算例分析的基础上得到以下结论：

1）区域电网新能源装机容量占比超过同步机，次同步风险增大。基于该区域电网的实际算例分析发现，新能源基地功率扰动或新能源基地输出功率提升都可能导致该地区电网产生次同步振荡事故。

2）提出了基于有源阻尼控制的区域电网新能源基地次同步振荡抑制方法。对区域新能源基地采用有源阻尼控制策略，可以有效抑制区域电网次同步振荡，提升电网运行安全性和稳定性。

3）给出了有源阻尼控制器的幅值校正及相位校正等关键环节的参数设计原则。有源阻尼控制器中，幅值校正系数K不宜过大，建议取[0，1]，滤波器时间常数T建议取（0.5，1），T1和T2根据振荡频率处相位校正角φ和校正阶数m由公式计算取值。