基于电磁-热-力多物理场仿真的铁心电抗器结构参数分层优化方法研究

陈 炜，吴晓文，袁发庭，曾继皓，肖 威，孙静玲

（1.湖南科技大学信息与电气工程学院，湖南湘潭 411201；2.三峡大学电气与新能源学院，湖北宜昌 443002）

0 引言

干式铁心电抗器作为电力系统的关键设备，在系统中应用广泛，其电压等级高和容量大的特征使得温升和振动等问题日益严重[1-3]。因此，在满足铁心电抗器电磁、温升和振动等性能技术参数要求下实现多目标优化成为工程需求问题。现有研究虽然能较好地揭示铁心电抗器电磁、温升和振动特性，但对于铁心电抗器整体性能优化的研究较少。因此，在保证铁心电抗器性能参数的前提下提出多目标优化方法至关重要。

在温升优化方面，袁召等结合空心电抗器包封线圈-气道单元的散热特点，提出提高线圈散热效率的优化方法，在保证温升恒定的同时可提高金属导体利用率[4]；Jacek 等基于有限元仿真及多目标遗传算法，通过调整线圈和气道的结构参数以降低线圈损耗[5-6]；文献[7]根据对流换热实验关联式推导出电抗器的温升计算方法，采用多岛遗传算法获得线圈的最佳结构参数。在振动优化方面，闫荣格等[8]学者建立串联电抗器的电磁-机械耦合模型，用数值方法计算电抗器铁心的振动加速度，提出了通过谐波注入的减振方式；律方成等人采用多物理场有限元仿真计算的方法[9]，研究了气隙结构对特高压并联电抗器铁心振动的影响规律，采用差异性排布方式能有效减少振动；在此基础上，文献[10]在建立准确的材料磁致伸缩模型，利用中心组合试验设计与有限元仿真相结合的方法，通过调整长度分布来实现降低振动。然而，铁心电抗器损耗温升和振动特性相互制约，结构参数的调整无法实现各性能参数达到最优值；现有方法侧重于对电抗器局部进行优化，无法实现电抗器整体性能的提升。

在多目标优化方面，文献[11]以电抗器金属导体用量为优化目标，在满足温升和振动性能参数要求下，提出了基于粒子群算法（Particle Swarm Optimization，PSO）；算法的绕组结构参数优化方法；张成芬等以电抗器金属导体用量和损耗作为优化目标，对传统的多目标遗传算法（Non-dominated Sorting Genetic Algorithm-II，NSGA-Ⅱ）算法加以改进，获得了最佳的绕组结构参数[12]。文献采用正交试验设计方法对铁心电抗器线圈结构进行优化，在满足电抗器电磁、温升及振动特性要求的情况下使绕组导体用量最小化，获得铁心电抗器线圈的最佳结构参数[13]。文献[14-15]综合考虑电抗器材料成本和运行成本最小化这两个相互冲突的目标函数，提出等式约束规划算法，将等式约束优化问题转换成无等式约束优化问题，提出了降低导线质量和损耗的优化方法。然而，铁心电抗器优化过程中需要考虑的结构参数众多，且涉及非线性和多目标问题，不可避免存在计算量大和寻优时间长等缺陷。

本文基于多物理场仿真计算方法，获得了铁心电抗器的电磁、温升和振动特性。在此基础上，提出了干式铁心电抗器多目标分层优化设计方法。通过灵敏度分析方法将结构参数分为两个层次，建立了铁心电抗器优化模型，基于响应面法（Response Surface Methodology，RSM）和NSGA-Ⅱ算法分别获得了分层后的最佳的铁心和绕组结构参数。结果表明铁心电抗器的温升、振动和金属导体用量显著降低，仿真结果验证了优化方法的准确性。

1 铁心电抗器结构参数及数学模型

1.1 铁心电抗器基本结构

本文的研究对象为干式铁心电抗器，额定电压为10 kV，采用自然风冷方式散热，模型如图1 所示。铁心电抗器主要由铁心和线圈两部分组成，其中线圈部分由多层筒式结构的扁铜线绕制而成，铁心中柱的气隙由环氧树脂材料填充，线圈导线匝数为112，层数为3 层，各层之间通过轴向气道散热。

图1 干式铁心电抗器结构图Fig.1 Structure diagram of dry core reactor

1.2 铁心电抗器数学模型

1.2.1 磁场计算

铁心电抗器线圈在交流电流作用下产生磁场[16]，满足Maxwell 方程组的瞬态电磁场方程，如式（1）所示：

式中：A为矢量磁位；υ为材料的磁阻率；J为绕组电流密度；x，y，z为方向向量；为电磁感应引起的涡流电流密度。

1.2.2 温升计算

干式铁心电抗器的热传递过程包括热传导、热对流和热辐射。结合铁心电抗器实际运行情况可知：在铁心及绕组区域，能量主要以热传导的形式在固体材料内部高温部分向低温部分传导；在电抗器绕组气道、绕组内表面、外表面以及铁心表面，热主要以热对流和热辐射形式进行传递[17]。

将磁场中计算得到的铁心绕组损耗作为流场-温度场的热源，可得电抗器传热控制方程[18]：

式中：T为温度；qw为单位时间流过单位面积的热流量；λx，λy，λz为材料沿x，y，z方向的导热系数；u，v，w分别为空气在x，y，z方向上的速度分量；h为空气的比焓；p为空气压力；V为流速矢量；j为耗散函数；Sh为空气由粘性作用而造成的机械能转换为热能的部分；qr为辐射热流密度；er为辐射率；dr为玻尔兹曼常数，取值为5.67×10-8W/（m2K4）；T1和T2为两辐射元件表面温度。

1.2.3 振动计算

根据虚位移原理可以计算得到铁心电抗器的电磁力F，如式（5）所示：

式中：dg为虚位移；F为电磁力。

铁心电抗器的振动频率主要在低频段，忽略阻尼力影响[19]，其振动方程可表示为：

式中：M为质量矩阵；K为刚度矩阵；X为待求的振动位移矢量；F（t）为电磁力矢量；σ为应力张量[20]。

2 铁心电抗器多物理场仿真计算

2.1 电磁场仿真结果

通过对铁心电抗器电磁、温度和振动分布进行研究，获得铁心电抗器的分布规律，为后续铁心电抗器的优化提供基础。

在电磁场仿真中设置电流激励条件，频率50 Hz，周期为0.02 s。电流达到峰值时铁心的磁通密度B分布如图2 所示。

图2 铁心磁密分布Fig.2 Magnetic density distribution of iron core

由图2 可知铁心电抗器铁心整体磁通密度成对称分布，在铁心中柱上呈上下对称分布趋势，磁通密度最大值位于铁窗拐角处靠近铁心中柱一侧，最大值为1.41 T。

图3 为线圈漏磁分布图。由图3 可知，干式铁心电抗器线圈的磁通密度在径向方向上由内到外逐渐降低，在轴向方向上磁通密度先增后减，最大磁通密度位于内层线圈中部，为0.14 T。

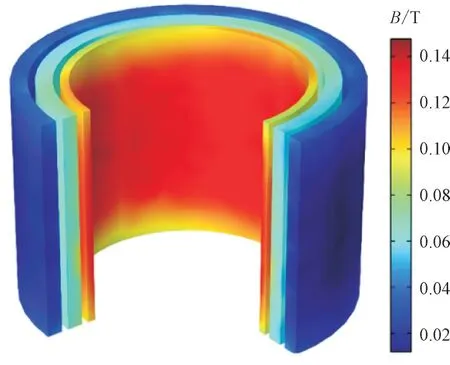
图3 线圈漏磁分布Fig.3 Magnetic flux leakage distribution of coil

2.2 温度场仿真结果

铁心电抗器流场-温度场采用瞬态仿真计算，将线圈和铁心损耗作为温度场热源，计算总时长设为15 h，时间步长为0.1 h。仿真运行15 h 后已经达到稳态，温度分布如图4 所示。通过仿真计算可知，铁心电抗器最高温升主要集中在绕组上，线圈温度明显高于铁心温度，其热点温度T为86.5 ℃。

图4 电抗器温度分布Fig.4 Distribution of reactor temperature

2.3 结构场仿真结果

铁心电抗器磁场-结构场仿真采用瞬态计算，将电磁场计算得到的电磁力作为结构场的激励，通过获得了电磁力最大时刻的铁心振动位移，仿真结果如图5 所示。

图5 铁心振动分布Fig.5 Vibration distribution of iron core

在线圈流过的周期电流为最大值时，铁心受到的电磁力最大，由图5 可知，旁扼的自由变形更为严重，最大值为0.40 μm。

图6 为线圈振动分布图。

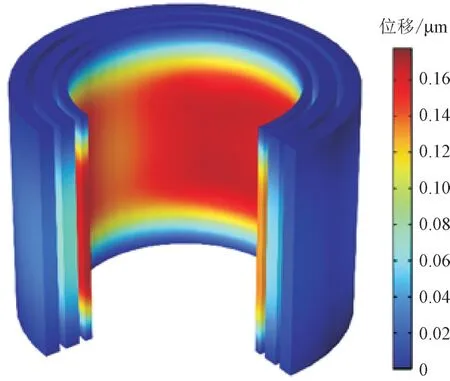
图6 线圈振动分布Fig.6 Distribution of coil vibration

由图6 可知，线圈受到的电磁力在径向方向上由内层到外层逐渐衰减，线圈的形变趋势在径向方向上向外扩张，轴向方向上由上下两侧向内挤压的趋势，在层线圈的中部位置处形变最为严重，最大形变位移为0.15 μm。

3 铁心电抗器结构参数分层优化方法

干式铁心电抗器的优化设计需要考虑多物理场性能参数是否满足要求。实际中铁心电抗器的设计要综合考虑温升、振动和损耗等指标，由于铁心电抗求的结构参数对电磁、温度和振动分布的影响规律复杂，对多变量多约束下进行寻优存在时间长的问题。与此同时，在多维迭代计算过程中，一些对目标影响较小的参数会影响迭代的收敛性，使优化收敛困难或者陷入局部最优解，导致计算精度难以满足设计要求。

3.1 优化模型的建立

为了得到实现铁心电抗器低成本、低损耗、轻质化的设计要求，分层优化方法为电抗器结构参数多目标优化问题提供了新的思路。

将铁心电抗器铁心材料用量m1、线圈导体用量m2、热点温度Tmax、最大振动位移X、电抗器铁损PFe和铜损PCu作为优化目标，具体的目标优化范围如表1 所示。

表1 电抗器的各性能参数范围设置Table 1 Reactor performance parameter range settings

选取合适的结构变量参数是优化的关键，现将线圈高度、气道宽度、气隙高度等11 个参数作为优化变量，其初始设计参数如表2 所示。

表2 铁心电抗器的主要变量参数Table 2 Main variable parameters of iron core reactor mm

为满足工程铁心电抗器电磁特性要求，控制铁心电抗器的电感值偏差不超过5%，铁心磁通密度不超过设定值，以防止饱和。约束条件设置如式（8）所示：

式中：Br为铁心磁密；UN为电源电压；f为电源频率；W为绕组匝数；Ac为铁心柱径向截面积；Bmax为铁心饱和磁通密度。

由于铁心电抗器的优化涉及多变量、多约束和多目标，为兼顾计算精度和计算效率的要求，采用拉丁超立方试验设计方法对铁心电抗器优化设计进行简化，该方法在高效的选择铁心电抗器最优结构参数组合基础上，结合灵敏度分析方法，可分析设计变量对于电抗器各物理场的影响程度，从而实现对结构参数的分层。具体优化流程如图7 所示。

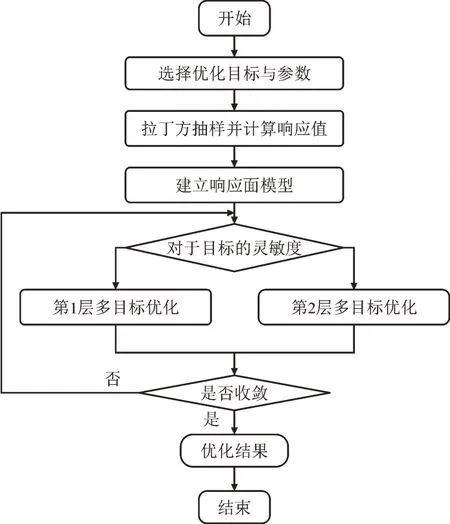
图7 优化流程Fig.7 Hierarchical optimization flowchart

通过拉丁超立方试验设计方法对干式铁心电抗器设计变量选取50 组样本组合，结合有限元仿真可以得到在不同结构参数下的电磁场、温度场、结构场的仿真结果。

3.2 灵敏度分析

采用灵敏度分析技术来研究结构参数对铁心电抗器质量、损耗及电磁、温升和振动等特性的影响规律，根据其相关程度，选取相关程度较高的参数进行下一步优化，从而实现铁心电抗器优化设计的参数降维。其中，灵敏度指标Si定义为[21]

式中：Xi为设计变量；Y为各个系统的状态变量值；Var(E(Y|Xi))为E(Y|Xi)的无条件方差；Var(Y)为Y的无条件方差。

通过式（9）可以定量得到各结构参数对铁心电抗器各物理场特性指标的影响程度即灵敏度，灵敏度越大对状态变量的影响程度越大。基于得到组样本数据，建立设计参数与状态变量的响应关系，从而计算得到归一化后的灵敏度结果，如图8 所示。

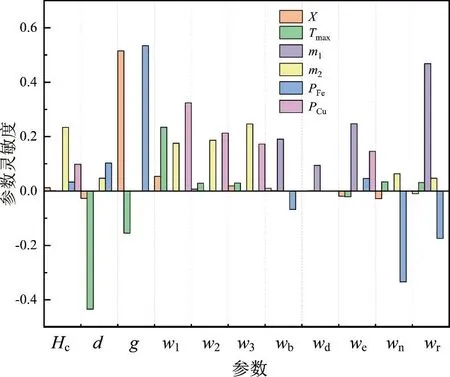
图8 灵敏度分析Fig.8 Parameter sensitivity analysis

根据参数灵敏度分析可得：Hc，d，w1，w2和w3对于热点温升Tmax，线圈导体用量m2和铜损PCu的灵敏度较高，因此将Hc，d，w1，w2和w3作为第1 层优化变量，将Tmax，m2和PCu作为第1 层优化目标，其数学模型如式（10）和式（11）所示：

铁心电抗器结构参数g，wb，wd，we，wn和wr对于X，m1和PFe的灵敏度较高，因此将g，wb，wd，we，wn和wr作为第二层优化变量，将X，m1和PFe作为第二层优化目标，其数学模型如式（12）和式（13）所示：

式中：x1，x2分别为第1 和第2 层的优化变量；f1(x1)和f2(x2)为对应的函数。

基于设计变量对各物理场的影响程度，将设计变量分为两个层次，将多维的非线性优化问题简化为多个子空间彼此独立地进行优化，可极大缩短仿真计算时间。

3.3 分层优化方法

为进一步减少了进行多物理场仿真计算和多目标寻优时长，本文采用RSM 来描述设计目标与变量之间的关系。工程中常用二次多项式模型进行建模分析，保证模型在具有较高精度的同时模型不过于复杂[22]。响应面模型如式（14）所示：

式中：φ(x)为目标函数；k为试验变量的个数；β0为常数项；βi，βii和βij分别为一阶，二阶和二阶交互项系数；ε为误差的恒定值。

为有效实现对铁心电抗器多目标优化，采用多目标遗传算法NSGA-Ⅱ，对设计参数进行全局优化搜索，将种群大小N 设置为50 将最大迭代次数设置为100，算法流程如图9 所示[23]。

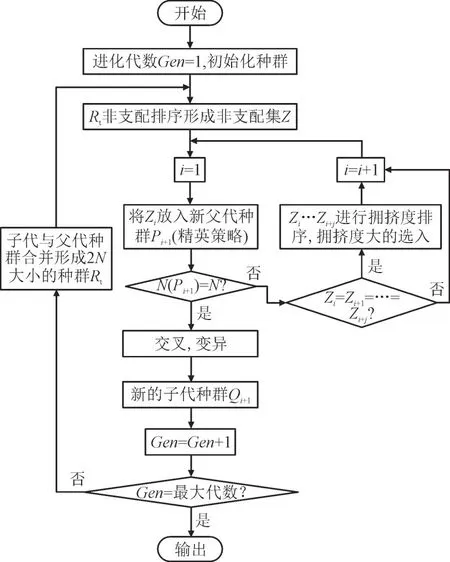
图9 NSGA-II算法流程Fig.9 Flowchart of NSGA-II algorithm

3.3.1 第1层优化设计

利用样本数据，根据响应面法拟合得到第一层参数的响应面模型，图10 为第一层优化变量d和Hc关于PCu响应面图，图11 为d和w1关于Tmax的响应面图。Gen 为进化代数，i，j为迭代次数i，j取1，2，3，……。

图10 d和Hc与PCu间的响应关系Fig.10 Response relationship among d，Hc and PCu

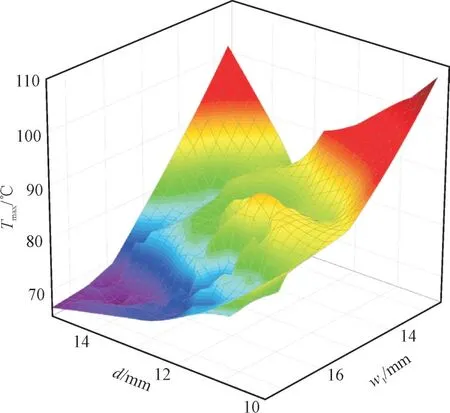
图11 d和w1与Tmax间的响应关系Fig.11 Response relationship among d，w1 and Tmax

根据铁心电抗器优化变量的取值范围和响应面模型，采用多目标遗传算法获取第一层优化模型的Pareto 可行解，优化结果如图12 所示。

图12 第一层优化的Pareto可行解Fig.12 Pareto feasible solution of the first layer optimization result

对可行解进行提取，经迭代收敛后可以获得第一层的铁心电抗器最佳结构参数，如表3 所示。

3.3.2 第二层优化设计

根据响应面法拟合得到第二层参数的响应面模型，图13 为第二层优化变量wd和wn关于最大振动位移X的应面图，图14 为d和w1关于热点温度Tmax的响应面图[24]。

图13 wd和wn与X的响应关系Fig.13 Response relationship among wd，wn and X

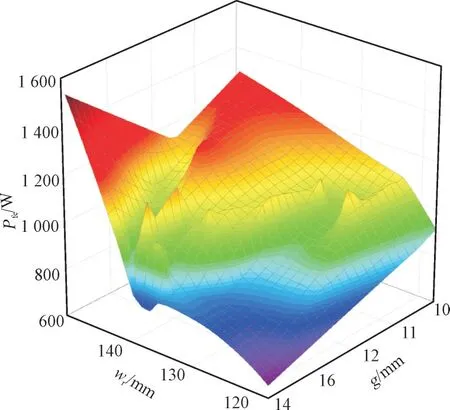
图14 wr和g与PFe的响应关系Fig.14 Response relationship among wr，g and PFe

采用多目标遗传算法寻优[25-27]，通过第二层优化模型可以获得剩余6 个变量参数，第二层优化结果的Pareto 可行解如图15 所示。

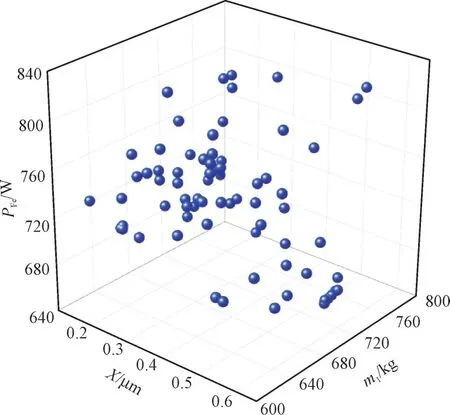
图15 第二层优化结果的Pareto可行解Fig.15 Pareto feasible solution of the second layer optimization result

对可行解进行提取，经迭代收敛后得到设计变量的优化值，如表4 所示。

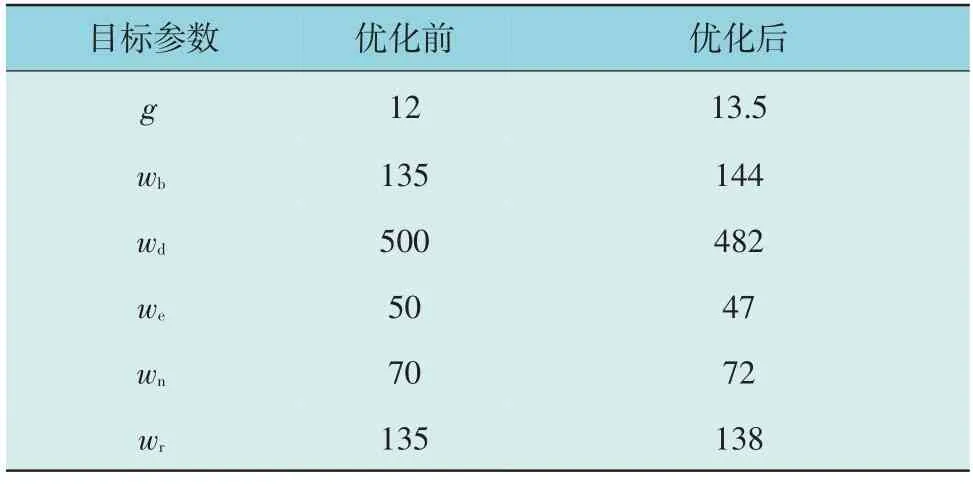
表4 第2层优化结果Table 4 The second layer optimization results mm

3.3.3 优化结果

干式铁心电抗器的优化设计需要考虑电抗器整体的电磁特性、温升特性、振动特性，分层优化设计利用响应面模型构建了铁心电抗器结构参数与优化目标间的响应关系，综合考虑铁心电抗器成本和损耗，最终获得了铁心电抗器优化前后的性能目标对比结果，如表5 所示。

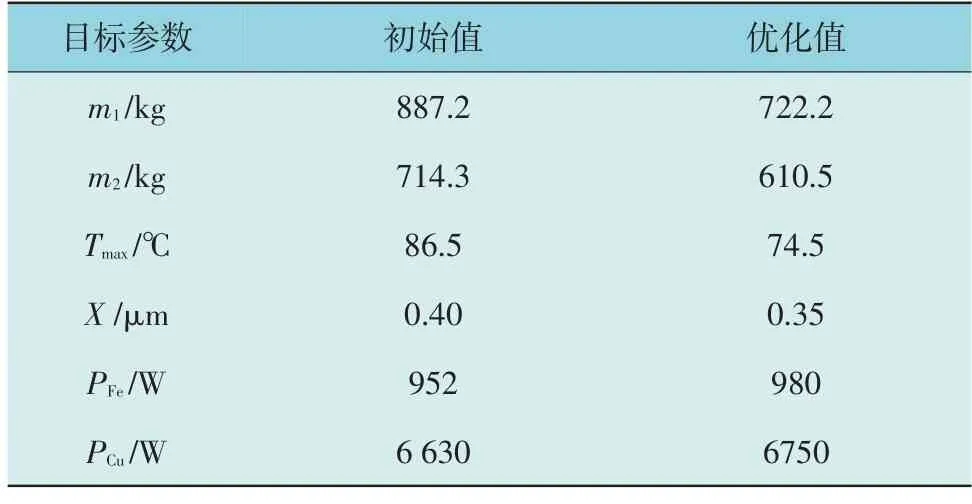
表5 优化结果对比Table 5 Comparison of optimization results

由上表可知，电抗器铁心质量和线圈质量分别降低18.6%和14.5%，热点温度降低13.9%，最大振动位移降低12.5%，铁损和铜损分别增大2.9%和1.8%，优化后各项性能参数均满足设计要求。

3.3.4 分层优化与整体优化结果对比

对于干式铁心电抗器而言，各个子系统之间存在着非线性关系、且子结构之间耦合性强弱各不相同，导致在多目标优化设计中，目标函数、约束函数与设计变量之间的关系复杂，各子目标函数相互关联甚至相互矛盾。为了验证分层优化方案的优越性，本文分别对整体优化方案和分层优化方案进行对比，结果如表6 所示。

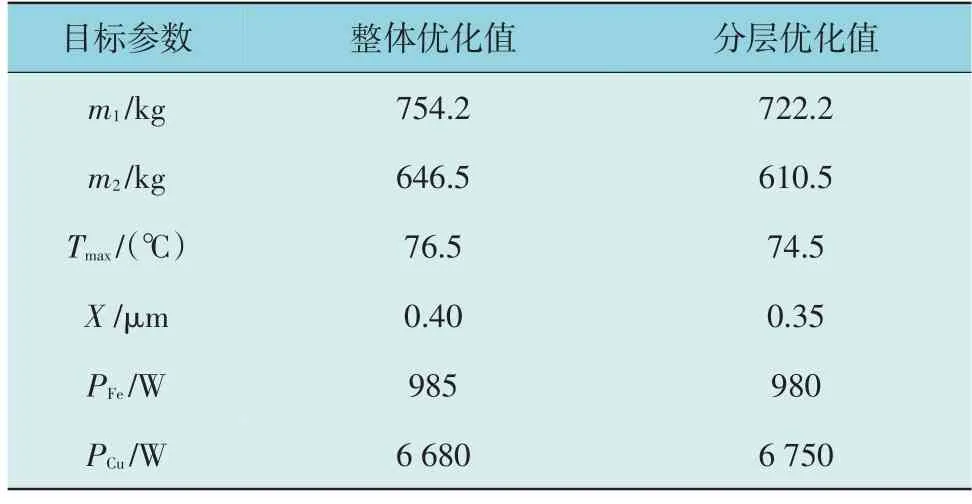
表6 分层优化与整体优化对比Table 6 Comparison of hierarchical optimization and overall optimization

分析优化结果可知，整体优化方案各性能指标优化效果较差，且线圈导体质量和温度优化结果不满足设计要求，分层优化结果明显优于整体优化结果。

3.4 仿真验证

为了验证设计优化的有效性和准确性，根据优化后的结构参数，建立了干式铁心电抗器三维仿真模型，得到其温度和振动位移分布结果，如图16 所示。

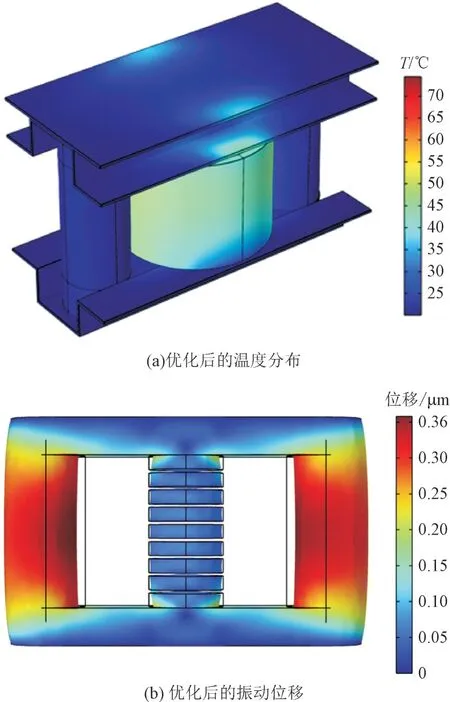
图16 最优参数下的优化结果Fig.16 Optimization results under optimal parameters

由图16 可知，优化后铁心电抗器最大振动位移仿真结果为0.36 μm，最高温度仿真结果为73.5℃；采用响应面模型计算得到的最大振动位移为0.35 μm，最高温度为74.5℃，最大误差不超过3.0%，且电感满足要求，因此，仿真结果验证了优化方法的准确性。

4 结论

本文基于多物理场仿真计算方法，提出了铁心电抗器分层优化方法，获得了最佳的结构参数，可以得到以下结论：

1）建立了铁心电抗器的三维仿真模型，获得其铁心电抗器磁通密度、温度和振动位移分布，其最高温度为86.5℃，位于内层线圈上，最大振动位移为0.40 μm，位于铁心旁扼处。

2）将实验设计和多物理场仿真相结合，得到了各结构参数对铁心电抗器温升、振动等众多指标的影响规律。基于灵敏度分析得到电抗器温度受气道宽度的影响最大，气隙高度对铁损的影响显著。

3）建立了铁心电抗器结构参数分层优化模型，基于RSM 响应面法和NSGA-Ⅱ算法分别获得了分层后的最佳的铁心和绕组结构参数，结果表明铁心电抗器铁心质量和线圈质量分别降低18.6%和14.5%，热点温度降低13.9%，最大振动位移降低12.5%。