基于等效简化和GPU的高比例新能源电网快速仿真系统

路学刚，朱欣春，胡 斌，董诗焘，文兆新，毛东宇，郑宗生

（1.云南电力调度控制中心，云南昆明 650000；2.南京南瑞继保电气有限公司，江苏南京 211102；3.四川大学，四川成都 610065）

0 引言

随着我国新能源的迅速发展，电网的新能源比例逐渐提高，大规模电力电子设备的控制特性对电网整体运行特性的影响日益显著[1-2]。多种时间尺度动态特性耦合、设备规模增大以及电网网络的复杂性极大增加了电网分析的难度[3-5]。

电网系统仿真是准确掌握电网运行特性必备的基本手段，但当前国内外已有的仿真工具均存在一定的局限性[6-7]。电网常用的BPA 等机电仿真程序可以适用大规模电网仿真，但无法详细考虑对直流输电系统和新能源场站变流器等电力电子设备的动态特性。PSCAD，MATLAB 等电磁仿真软件可以搭建较为详细复杂的电力电子控制系统模型[8]，可以充分反映电力电子设备的实际运行动态特性，但由于软件运行算法的限制，无法适应较大的高比例电网仿真。RTDS 可以进行复杂的电磁暂态仿真[8]，但其运行实施需要大量的配套和维护工作，无法适应频繁的电网分析需求。

仿真系统的研究主要包括仿真模型和仿真算法两方面。仿真模型方面，适应于大规模仿真的新能源变流器集群，直流输电等电力电子装备及其保护系统的建模方法仍是目前的研究热点。文献[9-10]研究了电力电子设备电磁暂态模型的简化，通过开关函数或平均化等实现运算加速。文献[11-12]通过不同频次动态相量的建模方法，加快了电磁暂态的计算。文献[13-14]采用移频建模的方式提高仿真步长，实现电磁暂态的加速。文献[15-16]通过人工智能算法和大数据的方式实现大规模场站的特性建模。仿真算法方面，利用多线程结合并行计算算法对大电网进行仿真，是提高电磁暂态仿真效率的有效的方式。文献[17-19]基于矩阵分网实现了仿真计算的并行。文献[20-22]利用GPU 加速实现交流潮流法的加速计算。文献[23-24]在多速率并行计算基础上，基于高性能服务器和现场可编程门阵列（Field Programmable Gate Array，FPGA）实现了仿真并行计算。综合已有的研究，当前电力电子设备的电磁暂态模型的精细化程度仍有待提高。网络计算、设备建模与并行计算的结合仍有进一步的研究空间，共同实现精确、快速和便利的仿真系统。

为解决当前高比例新能源电网仿真系统在高精度、快速和便利性方面面临的问题，本文提出基于等效简化和GPU 的高比例新能源电网快速仿真系统。基于控制模型和联结阻抗对大规模变流器设备进行聚合等效，对电网结构进行分区简化，进一步降低运算复杂度；通过GPU 并行算法完成仿真建模和计算，提高仿真系统的运行速度；有效结合聚合等效建模、分区简化和并行算法，保证电磁暂态仿真精度，提高大规模复杂电网的仿真速度，适应了电网对仿真分析的高频使用及维护。

1 快速仿真系统架构

针对高比例新能源电网的快速精确仿真需求本文所提仿真系统，同时兼顾仿真模型、仿真工程维护和进行的便利性。仿真系统整体架构如图1所示。通过多变流器的聚合建模和系统网络的分区简化，在保证电力电子设备动态特性的前提下，尽可能简化仿真内容；通过GPU 电磁暂态时间尺度并行计算提高整体仿真效率，实现仿真过程的加速。以聚合等效建模、网络简化和GPU 并行计算为核心技术，构建相应的软硬件，完成电网所需的仿真分析计算。

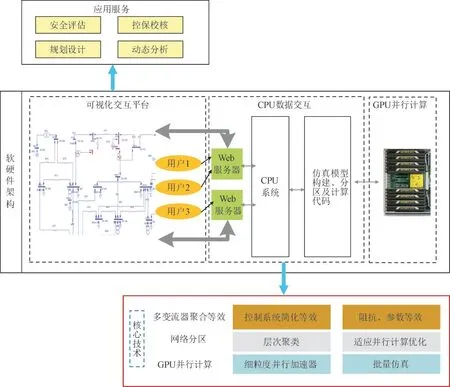
图1 仿真系统整体架构Fig.1 Architecture of proposed simulation system

仿真平台即软硬件系统主要包含3 部分功能：人机可视化交互、数据交互以及并行计算。人机可视化交互提供仿真任务构建平台，搭建网络架构，定义元器件及其控制模型，完成仿真任务设计，可以进行批量任务设计，并形成拓扑和元件信息进入数据交互模块；数据交互主要包含模型、算法以及任务信息的交互，通过网络及通讯协议完成核心模型和算法的维护、更新及调用，接收仿真任务及其信息，并按照对应的模型和简化算法对各个仿真任务中包含的新能源场站及系统网络进行简化，同时生成仿真任务集与并行计算硬件模块进行交互，收集仿真结果并反映至人机可视化交互界面；并行计算模块基于GPU 异构并行计算环境，将各个任务的并行运算映射到GPU 中进行计算，并将计算结果返回至数据交互模块。仿真平台通过网络进行信息交互，实现人机交互和复杂计算，易于平台计算能力的扩展，也便于模型和算法的更新维护，可以较好适应大规模仿真任务的需求。

2 多变流器聚合等效

随着变流器并网数量的增多，弱阻尼工况下的故障等电磁暂态现象是重要的仿真内容。

对新能源场站进行聚合等效，在对新能源高占比系统特性分析和测试应用的前提背景下，优先满足等效前后电压、电流、总体输出有功无功功率保持不变，等效变流器与整体变流器动态特性保持一致。本仿真系统对多变流器聚合等效的基本思路如下：

1）简化认为多变流器内部控制系统及其电气参数相同，对于控制参数差异较大的变流器进行单独聚合等效。

2）当变流器的差异主要是场站内的连接阻抗时，按近机群与远机群的分类将场站内机组等值为2 机。

3）当变流器的差异主要是各变流器输出有功和无功功率时，按大功率机群与小功率机群的分类将场站内机组等值为2 机。

4）当场站内电气特性复杂时，按照近机群、远机群、大功率机群、小功率机群将场站内机组等值为4 机。

2.1 变流器控制系统模型

图2 为单变流器并网系统以有功无功为控制目标的典型控制系统。

图2 典型变流器有功无功控制系统Fig.2 Active and reactive power control system of typical converter

系统的电压外环控制包括有功控制和无功控制2 个环节。有功控制环节常采用直流电压控制，无功控制环节常采用交流侧端电压控制。内环控制为d，q轴电流环控制。

为实现矢量控制，系统利用锁相环检测并网点电压Ut的相位，继而生成控制参考坐标系。图3 为基于d，q同步坐标变换的三相同步锁相环控制框图。其中，ω0为系统额定角速度；Utd、Utq分别为系统电压Ut的d，q分量。

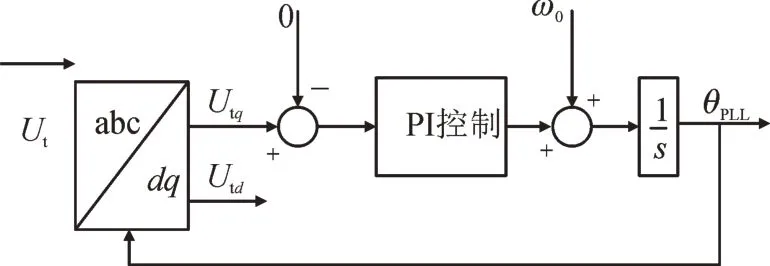
图3 锁相环控制框图Fig.3 PLL control structure

2.2 多并联变流器聚集模型

将多变流器等效为单台变流器，在控制模型及其参数默认一致的情况下，等效的单机变流器即可采用原单台的控制参数。为保证聚合等效输出的精度，需要考虑光伏/风电等新能源机组参数、场站连接线路阻抗等元件的聚合。

对于新能源机组，基于新能源场站模型结构，参考实测曲线，可以得到其聚合模型参数的等效关系：

式中：N为待聚合光伏/风电机组数量；Si，Pi，Qi，Hi，Di，Cdi，Lfi分别为第i个光伏/风电机组输出的视在功率，有功功率，无功功率，惯性常数（风机），阻尼系数，滤波电容，滤波电抗；Seq，Peq，Qeq，Heq，Deq，Cdeq，Lfeq分别为聚合后单光伏/风电机组输出的视在功率，有功功率，无功功率，惯性常数（风机），阻尼系数，滤波电容，滤波电抗。

新能源机组存在不同的连接方式。阻抗等效的基础为保证变换前后由受电网电压影响的幅值和相位不变。对于变压器，可等效成对应电压侧的阻抗，加入连接阻抗进行统一变换。

干式线路等值如图4 所示，其中，S1，S2，S3，S4代表各风电机组。当功率平均分布时，干式线路等值阻抗如式（2）所示。

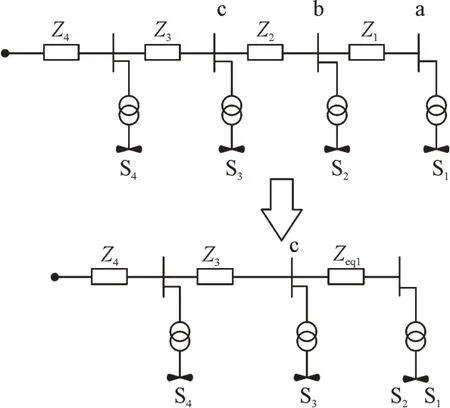
图4 干式线路等值图Fig.4 Equivalent model of dry lines

式中：Zeq为等效阻抗；Z1，Z2，…，Zn为各变流器的连接阻抗；n为变流器数量。

放射式线路等值如图5 所示。当功率平均分布时，放射线路等值阻抗如式（3）所示。

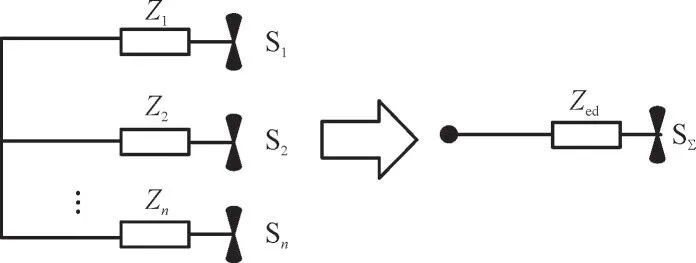
图5 放射式线路等值图Fig.5 Equivalent model of divergent lines

式中：Zeq为等效阻抗；Z1，Z2，…，Zn为各变流器的连接阻抗；n为变流器数量。

对于系统故障的仿真，涉及变流器机组数量变化的工况，则需要针对性调整数量N，重新对多变流器机组进行聚合等效。

3 网络分区

通过优化网络分区的方式可以提高并行仿真的计算速度。在对系统网络进行分区后，并行仿真计算速度受各分区单独的仿真时间和各分区之间数据交互时间的影响。仿真运行总时间与2 个因素的关系可由式（4）表示：

各分区单独的仿真时间和各分区之间数据的交互时间与采用的GPU 处理能力相关。因此在本文仿真系统中将GPU 处理能力作为网络分区的基础依据。由式（4）可知，各分区间的规模尺度要尽量均匀，避免各分区计算差异过大及相互间交互时间的不同。本文通过所有仿真任务中涉及元件的总数量来表征仿真规模。电网各元件种类、控制策略不同，其仿真计算所需时间也不一致。但相同类型、细度元件的计算时间相当，计算量差距很小；而不同类型元件的计算量差距很大。在高比例新能源电网中，主要是电力电子设备和同步机的差距较大，因此为充分考虑新能源场站节点在仿真中的计算量，在涉及元件数量的计算中，新能源节点需要计算一定的系数。同时，根据第2 节中变流器等效，等效出的变流器即可按单独的元件计算。将仿真任务中的元件总数与当前GPU 可用线程块计算元件处理平均数，作为网络分区的基础依据，计算如式（5）所示。

式中：M为线程块计算元件处理平均数；Nb为当前可用GPU 线程块；j为仿真任务标号；αj为第j个任务中变流器附加系数，一般大于1；Ngi为第j个仿真任务中的同步机数量；Nlj为第j个仿真任务中的负荷数量；Nt为当前并发的仿真任务数量。

本文采用层次聚类方法对系统网络进行分区，将具有指标关联特性（例如电气联系紧密，属于同一地理区域或行政管辖范围等）的节点和元件聚合在一起，对大系统进行分区。将监控调度系统中省级以上电网中电力系统网络连接关系、地理分区名及元件类型等信息导入仿真数据。将电气距离或/且地理距离较近的进行聚合，对于含Nm个节点的大系统，如图6 所示，从电力系统所有节点开始，将具有关联特性的节点由下至上划分为不同的分区，不断向上直至完成所有网络的分区工作，其中，C1，C2等代表较高层级的聚类。

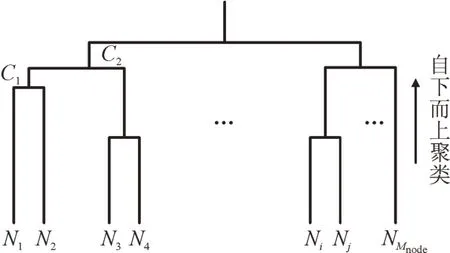
图6 自下而上层级聚类Fig.6 Bottom-up clustering

按照仿真任务中的网络，从最底端开始按照区域电气距离和电压等级进行排序。从最近的电气距离开始，将包含M个元件的节点作为1 个分区，直至所有网络的分区完成，分区的具体流程如图7所示。

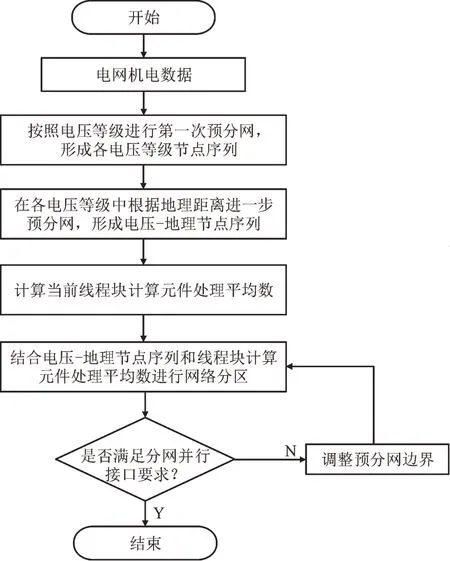
图7 网络分区流程Fig.7 Network partitioning process

4 GPU并行算法

GPU 是一类由大量计算核心、少量逻辑处理单元构成的众核（Many-Core）架构处理器。其为实现对GPU 的编程应用，NVIDIA 推出了统一计算设备架构（Compute Unified Device Architecture，CUDA）的通用并行计算架构，可以实现通过GPU 的强大计算能力来解决特定复杂问题。图8 给出了CUDA 下的GPU 细粒度并行计算模型。其中，GPU 程序被组织为一系列核函数。每一个核函数包含大量计算线程，并由CPU 程序调用执行。大量线程在GPU中被组织为层状结构，并有序地映射到GPU 中的每个计算核心。计算指令相同的线程通过单指令多线程（Single-instruction Multi-threads，SIMT）并行机制实现计算任务的细粒度并行。

图8 GPU细粒度并行计算模型Fig.8 GPU fine-grained parallel computing model

元件特性采用微分方程或偏微分方程来描述。一般先在待求解网络中采用数值积分方法（可选多种数值积分方法）对系统中动态元件的微分方程进行差分化，得到代数形式的差分方程组，进而得到等效导纳与电流源并联的诺顿等效电路，实现各个离散时间点上的暂态等值计算网络表征。通过联立电路的差分方程组，可以得到如式（6）所示的节点计算方程，求解可得系统中各节点电压的瞬时值。

式中：U1(t)，U2(t)，…，UN(t)为t时刻各节点电压；Y11～YNN组成等值网络的节点电导矩阵；I1(t)，I2(t)，…，IN(t)为t时刻为各节点注入电流。

面向控制系统和非线性电气元件的处理，其作用是更新电气元件计算所需的电压、电流、导纳矩阵。

将所得分区映射到不同的GPU 线程块中求解，各区的交互信息通过GPU 内存实现共享和调用。每个分区具有独立的仿真进程，将生成独立的电磁暂态仿真执行文件，调用GPU 网络求解核函数，并在不同的GPU 线程块上独立运行。网络方程采用任意GPU 加速的线性代数库求解式（6）所示的节点电压方程。为避免系统矩阵的频繁更新，在求解前，通过对系统节点电导矩阵Yn求逆，得到系统的节点电阻矩阵，并将其预存在GPU 全局内存中。在仿真过程中，若Yn不变，则节点电压方程的求解可简化为矩阵向量乘法。网络方程求解核函数可选用CUBLAS 矩阵求解器。同类计算采用SIMT 的细粒度并行计算形式在GPU 上求解。每层的不同类别元件可分至不同的组，实现分组SIMT 并行。每一层元件计算完毕后，进行一次层间同步，保证下一层所需的数据已准备完毕。最终，基于GPU 的电磁暂态仿真计算流程如图9 所示。其中，t为迭代次数；ttotal为迭代总次数。

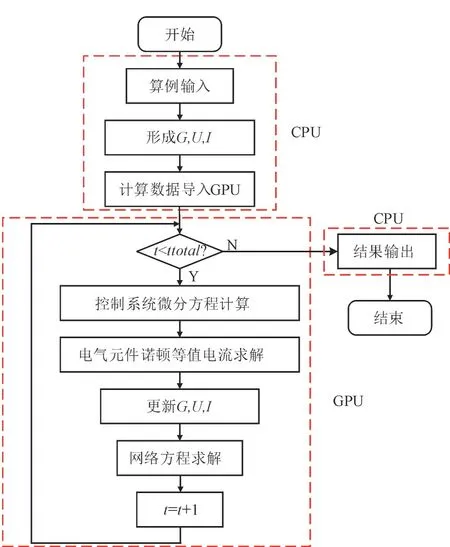
图9 基于GPU的电磁暂态仿真计算流程Fig.9 GPU based electromagnetic transient simulation calculation process

5 运行实例

为对高比例新能源电网快速仿真系统的运行性能进行测试，本系统采用NVIDIA A100 PCIe 80G作为仿真计算平台的GPU。从变流器仿真精度和仿真运行时间的角度进行实例验证。

为验证变流器等效方法的可靠性，将多变流器与等效变流器的运行情况进行对比。多变流器与电网连接的系统如图10 所示。以多变流器的电网系统的PSCAD 仿真结果作为测试依据，分别将正常运行、阶跃和故障3 种工况的运行情况与仿真系统中的等效变流器运行情况进行比较，对等效模型在稳态和暂态下的仿真精度和有效性进行验证。

图10 多变流器系统图Fig.10 Multi converter system

变流器控制采用有功/无功控制的方式，其主要控制和电路参数如表1 所示。为较好验证等效变流器的运行特性及更好模拟现场的连接情况，图10中各个变流器的阻抗存在差异。

表1 变流器的主要控制和电路参数Table 1 Main control and circuit parameters of converter

选取变流器的控制目标有功功率和无功功率作为比较对象，稳态运行情况下的波形对比如图11所示。其中，Pm0，Qm0为PSCAD 仿真结果，Pm，Qm为仿真系统仿真结果。从图11 中可以看出，稳态情况下等效变流器与多变流器的PSCAD 的仿真结果基本一致，误差不超过0.1%。

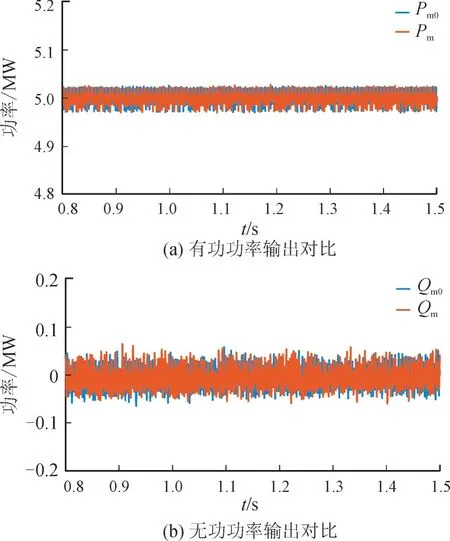
图11 稳态运行对比Fig.11 Steady state operation comparison

多变流器控制目标阶跃与等效变流器阶跃的输出波形对比如图12 所示。0.8 s 时刻有功功率降低10%，1.2 s 时刻返回原控制目标。从图12 中可以看出，阶跃情况下等效变流器与多变流器的PSCAD 的仿真结果基本一致，误差不超过0.1%。

图12 阶跃运行对比Fig.12 Step state operation comparison

为进一步验证仿真系统对变流器暂态工况的仿真能力，将系统三相短路系统电压降低至30%并持续0.5 s 的工况下的PSCAD 与仿真系统的仿真结果进行对比，对比结果如图13 所示。在整个暂态变化过程中，PSCAD 仿真结果与仿真系统的运行结果基本一致，有功/无功功率波动的最大最小值，波动形式误差较小。

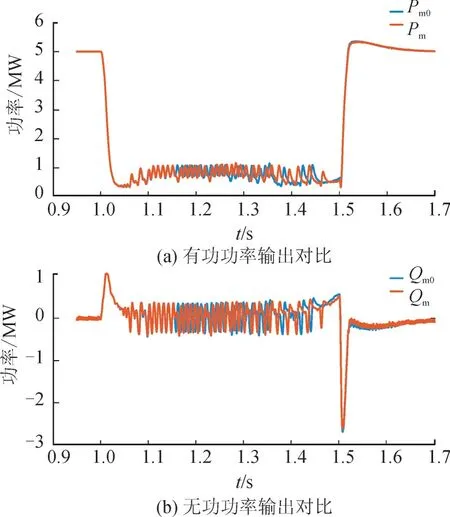
图13 故障运行对比Fig.13 Fault state operation comparison

对稳态运行、阶跃控制和三相故障短路典型工况下的运行对比表明，本文所提仿真系统的变流器等效及其接入电网后对应的电路运算，与采用传统的PSCAD 电磁暂态仿真程序运行的结果基本一致，具备在简化变流器情况下高精度展示高比例新能源电网电磁暂态过程的能力。

为测试高比例新能源电网快速仿真系统的运算效率，选取某地区的329 节点实际作为测试对象，该系统中新能源发电容量比例约为70%。在对电网的分区过程中，先按电压等级形成不同的序列，在各个序列中按照地理相近因素进一步形成对应的子序列，在其中按照第4 节所述的线程块计算元件处理平均数原则进行分区。对采用相同GPU核心数情况下不同变流器数量的仿真时间以及相同接入变流器情况下不同GPU 核心数情况下的仿真时间进行对比，分析并行计算运行特性。

将GPU 中并行运行的Block 设置为85，将各仿真工况下单位步长耗时进行对比，仿真工况包括：（1）新能源发电容量比例约为20%，通过切除一部分新能源电场和将小容量新能源电场替换成同容量的同步发电机实现；（2）新能源发电容量比例约为50%；（3）新能源发电容量比例约为70%。3 种工况下的单位步长耗时对比如图14 所示。从对比可以看出，在相同并行计算线程块Block 情况下，随着变流器数量的增加，计算时间有轻微的增加，但其运行时间要大大优于当前的电磁暂态仿真软件，符合电网规划、分析、调度等运行需求。

图14 不同新能源比例下仿真时间对比Fig.14 Simulation time comparison of different proportions of renewable energy

图15 为在新能源发电容量比例约为70%情况下针对不同并列运行Block 数量（85，50，20）的单位步长耗时的对比。从图15 中可以看出，随着并行数量的增大，可以提高仿真的运行效率，以此类推其可用于大规模电网的仿真分析。

图15 不同线程块下仿真时间对比Fig.15 Simulation time comparison of different thread blocks

综合实例运行分析，可以看出，所提出的仿真系统在适当等效多变流器的情况下可以保证合适的电磁暂态仿真精度，GPU 并行运算技术的应用可以大幅提高高比例新能源电网的运行时间，使得仿真系统可以用于电网快速的分析计算，具有较好的便利性，易于维护，与当前电网分析的精度和高频使用需求相契合，为具备电力电子设备特性的电网的规划、分析和调度等提供有力支撑。

6 结语

高比例新能源电网的运行特性分析包含大量的电磁暂态计算，为提高其仿真效率适应电网的分析需求，本文提出基于等效简化和GPU 的高比例新能源电网快速仿真系统，在保证完整控制模型前提下对大规模变流器设备进行聚合等效，保证电磁暂态特性的同时简化多变流器的仿真规模；对电网结构进行分区简化，以便于进行并行计算；仿真运算通过GPU 并行计算完成，提高仿真系统的运行速度；通过聚合等效、分区简化和并行计算的相互结合，实现高比例新能源电网的快速仿真，准确快速对高比例新能源电网的运行特性进行分析，使用便利，维护方便。最后通过运行实例，验证了所提仿真系统具有较好的精度和运行效率，适应大规模电磁暂态的快速仿真，满足电网规划、分析和调度等的需求。