基于时间序列神经分层插值模型的光伏功率超短期多步预测

李 楠，刘佳佳，赖心怡，杨志远，王泽亮，文福拴

（1.国网湖北荆门供电公司，湖北荆门 448000；2.浙江大学海南研究院，海南三亚 572025）

0 引言

随着全球能源结构转型的推进和可再生能源的快速发展，如何精确预测光伏出力成为了提高能源利用效率和电网稳定性的关键挑战[1]。然而，由于光伏发电的高度不确定性和外部环境因素的复杂性[2-3]，预测的准确性和可靠性仍亟待提高。

现有的光伏功率预测方法主要可分为基于统计的方法、基于传统机器学习的方法和基于深度学习的方法3 类。在统计模型中，自回归整合滑动平均（Autoregressive Integrated Moving Average，ARIMA）模型[4]和多周期时间序列分解（Multiple Seasonal-Trend decomposition using Loess，MSTL）算法[5]被广泛应用于光伏预测任务。然而，大部分统计模型主要针对单变量时间序列分析，尽管可以通过某些改进来处理多变量时间序列的预测问题，但通常仍难以取得准确的预测结果。支持向量回归（Support Vector Regression，SVR）[6-7]、极端梯度提升（Extreme Gradient Boosting，XGBoost）[8-9]和轻量级梯度提升机（Light Gradient Boosting Machine，LightGBM）[10-11]等机器学习模型适用于处理多变量时间序列问题，但往往不能有效地模拟历史数据或历史时间间隔与未来数据之间的潜在关联性[12]。近年来，随着数据量的爆炸式增长和计算能力的显著提升，越来越多的研究聚焦于利用深度学习技术提高预测模型的算法精度和效率[13-16]。文献[17]提出1 种基于个性化联邦学习（Personalized Federated Learning，PFL）的长短期记忆网络（Long Short-Term Memory，LSTM）框架，用于整县范围内的光伏出力及负荷功率预测。文献[18]分别采用LSTM、双向长短期记忆网络（Bidirectional LSTM，BiLSTM）和时间卷积网络（Temporal Convolutional Network，TCN）对光伏功率、电压和光伏组件效率进行预测，实验结果表明TCN 在预测准确性和效率方面均表现最佳。上述深度学习网络在处理长时间序列预测时常常面临计算复杂度高、模型适应性不强和难以捕捉长期依赖关系的挑战。此外，预测的准确性不仅依赖于模型本身的复杂性和精确度，对数据预处理和外生变量分析的关注不足，在一定程度上会限制预测模型的性能和适用性[19-22]。文献[23]提出用于长序列光伏功率预测的太阳能混合器模型（Solar-Mixer），该模型包含异常检测和修正模块以及预测模块，Solar-Mixer 在多变量和单变量时间序列预测中都取得了优异的性能。文献[24]针对光伏电站数据采集过程中出现的数据异常或缺失问题，提出1 种基于皮尔逊相关系数（Pearson Correlation Coefficient，PCC）的插值方法来修复数据。

因此，与现有工作相比，本文提出1 种结合外生变量分析、数据质量控制和长时间序列预测模型的综合方法，提供1 个更为完整的超短期光伏功率多步预测方案。本研究提出1 种综合相关性度量（Integrated Correlation Measurement，ICM）指标对外生变量进行分析和筛选，确保仅将与光伏出力高度相关的变量纳入模型；使用基于K 近邻（K-Nearest Neighbors，KNN）算法和线性插值的数据处理策略，解决数据缺失问题；采用基于多尺度信号采样和分层插值的时间序列神经分层插值（Neural Hierarchical Interpolation for Time Series，N-HiTS）模型[25]增强对长序列数据的处理能力，实现光伏功率的高精度多步预测。

1 光伏数据处理

本文着重探讨光伏功率的超短期预测问题，光伏超短期预测一般指的是对未来0～4 h 内光伏功率输出的预测。准确的超短期预测能够为电网运营商提供时间窗口来调整电网负荷和发电计划，以应对可再生能源的不确定性和波动性。

然而，在时间序列预测领域，数据的质量和处理方式对预测结果的准确性有着不可忽视的影响。一方面，外生变量的合理利用能够显著提升模型的预测能力；另一方面，对异常数据的有效处理则是确保数据质量，进而提高预测准确度的关键步骤。

对于光伏出力预测而言，外生变量可能直接或间接地影响光伏电站的功率输出，将这些变量纳入模型有助于提高预测准确度。同时，需要识别并排除与光伏电站功率输出不具有统计显著性关联的外生变量，避免模型过于复杂，从而确保模型的泛化能力。静态外生变量是指在预测期间不随时间变化而变化的变量，如光伏板类型、地理位置；历史外生变量是指在预测开始前已确定且不受模型内部变量影响的变量，如气象历史数据；未来外生变量是指预计在未来出现但当前尚未实现的变量，通常基于预测或假设并不受模型当前或过去状态的影响，如气象预测数据。

光伏电站异常数据的产生主要来源于3 种情况：（1）冗余数据：由于存储或传输过程中的故障导致数据中出现重复记录的数据；（2）缺失数据：由于设备故障、通讯中断等导致数据的部分缺失；（3）离群数据：通常由测量设备的故障或在数据传输及转换过程中发生的误码现象引起，导致出现超出正常范围的数据或数据突变。这些情况导致经过异常值处理后往往会出现数据的缺失，数据的缺失情况主要分为某行的某（几）列数据由于突变越限被剔除导致的单组数据缺失以及数据采集环节出现严重故障导致的整行数据缺失2 类。其中，对于仅单组缺失的数据采用基于KNN 算法的数据补齐法进行重构，对于整行缺失的数据采用基于线性插值的数据补齐法进行重构。

1.1 外生变量相关性分析

统计学中通常通过计算相关系数对外生变量进行相关性分析，包括肯德尔相关系数（Kendall Rank Correlation Coefficient，KRCC）、斯皮尔曼秩相关系数（Spearman’s Rank Correlation Coefficient，SRCC）和PCC。相关系数的范围通常在-1～+1 之间，系数的符号表示变量间的负相关或正相关关系。通常将相关系数绝对值阈值设置为0.6，用于确定变量间是否高度相关。

KRCC 是一种用于衡量2 组数据间序位关联的非参数方法，用τ表示。KRCC 通过考察成对观测值间的一致性和不一致性量化变量之间的相关性[26]，因此可以在不依赖数据分布假设的前提下度量变量间的关系，即：

式中：s gn(∙)为符号函数；z为任意实数；Xi为变量X的观测数据序列中，索引为i的观测数据；Yj为变量Y的观测数据序列中，索引为j的观测数据；n为样本数目。

PCC 是衡量2 个变量线性相关程度的统计指标，作为一种参数方法用r表示，其计算基于变量的协方差与其各自标准差的乘积[27]。PCC 假设涉及的变量遵循正态分布并且为线性关系，因此其对极端值异常敏感，对于含有离群值的数据，PCC 可能会产生误导性的结果，PCC 的计算公式如式（3）所示：

SRCC 是一种衡量2 个变量间单调关系强度的有效非参数方法，用ρ表示。与基于数据分布假设的相关系数不同，SRCC 依赖于变量值的排名而非其实际数值，从而增强对离群值的鲁棒性。因此SRCC 适用于分析定序数据或不满足正态分布假设的数据集，在样本量较小的情况下也能提供可靠的相关性估计[28]，即：

式中：di为秩次差；分别为Xi和Yi从小到大排序后的秩次。

为比较全面地评估光伏数据与外生变量之间的相关性，这里提出用于筛选外生变量的ICM 指标。ICM 综合KRCC，PCC 和SRCC 的优点，通过计算归一化权重为不同类型的相关系数提供统一的框架，旨在捕捉变量间的相关性。ICM 的计算流程为：

1）对每个外生变量，分别计算其与目标变量的KRCC，PCC 和SRCC。

2）对于相关系数Γ ∈{τ,r,ρ}，由式（6）计算其归一化权重WΓ：

3）将每个外生变量的各相关系数分别乘以其归一化权重，求和得到ICM 指标MIC，即：

1.2 KNN算法

KNN 算法是一种基于邻近样本信息进行预测或分类的算法，在缺失数据的处理中被广泛应用[29]。在面对缺失值时，KNN 算法通过找到具有相似特征的邻近样本，利用这些样本的已知值来估计缺失值。KNN 算法填补缺失值的基本步骤为：（1）选定K值，即最近邻样本的数量；（2）对于含有缺失值的样本，计算其与完整数据集中每个样本之间的距离；（3）选择与含缺失值的样本距离最近的K个样本，形成邻近样本集合U={u1,u2,…,uK} ；（4）使用这些邻近样本的均值或众数填补缺失值。

通常采用欧氏距离衡量样本之间的距离。对于2 组d维数据p=（p1，p2，…，pd）和q=（q1，q2，…，qd），使用非缺失维度进行计算，即：

式中：o为非缺失维度的索引；O为非缺失维度的索引集合。

1.3 线性插值

在数据处理中，特别是在时间序列数据的处理中，线性插值被广泛应用于填补缺失值。线性插值算法基于以下假设：2 个已知点之间的变量变化是均匀的，因此可以用直线方程来估算两点之间任一点的值。对于2 个数据点(g1,h1) 和(g2,h2)，且g1≠g2，计算这2 点间某一点g对应值h的方法如式（9）所示：

2 N-HiTS模型

N-HiTS 模型是一种针对时间序列预测的深度学习架构，模型结构如图1 所示。本节将详细介绍N-HiTS 模型的组成部分，作为一种创新的架构，其应用多层感知机（Multilayer Perceptron，MLP）和双残差网络，通过多尺度信号采样和分层插值方法针对不同信号采样率的信号进行专门化的预测。

图1 N-HiTS模型结构Fig.1 Structure of the N-HiTS model

2.1 双残差网络

2.2 基本块

基本块第一部分为多尺度信号采样，通过最大池化层MaxPools,b的参数ps,b对输入信号ys,b在不同尺度上进行下采样，其目的是使得基本块能够关注不同信号采样率下的输入信号，即：

多尺度信号采样保持了原始的感受野，但通过限制基本块的输入信号规模，减少内存占用和计算量，并减少可学习参数的数量，从而减轻过拟合的影响。

大多数光伏功率预测模型将表达率设置为1，即模型为每一个预测时间点分别生成预测值，此时基准值θ的维度与预测值y的维度相同。这种方法能够为各时间点提供特定的预测，但同时需要大量的计算资源。为解决这个问题，N-HiTS 模型通过设置表达率小于1 的方式控制模型的输出，模型不再为每个预测时间点产生一个独立的输出参数，而是生成较少的参数，然后通过插值来恢复整个时间范围内的预测。

式中：t1和t2为具有前向预测基准值的相邻时刻。

2.3 堆栈

基本块被分组成堆栈，通过设置每个堆栈内基本块的表达率和池化层参数，从而获取特定的输入信号规模并进行插值恢复操作。本文通过将靠近原始输入信号的堆栈内基本块参数设置为较小的表达率和较大的池化层参数，可以使得靠近原始输入信号的堆栈更倾向于观察平滑的趋势信号从而得到低细节层次的信号，远离原始输入信号的堆栈内基本块具有较大的表达率和较小的池化层参数，从而捕捉信号的高细节层次。N-HiTS 模型的堆栈数量设置为3 时，各堆栈输出如图2 所示。

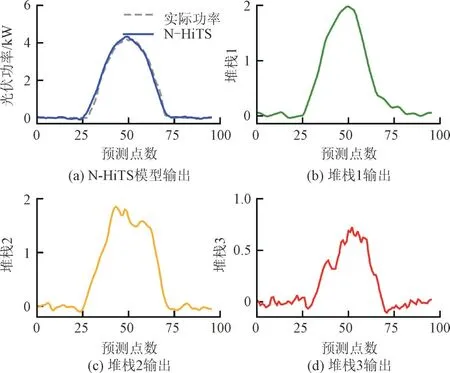
图2 堆栈数量为3时N-HiTS模型输出及其内部堆栈输出Fig.2 Output of the N-HiTS model with stack number of 3 and its internal stack outputs

3 算例与结果

3.1 数据说明

采用澳大利亚沙漠知识太阳能中心（Desert Knowledge Australia Solar Center，DKASC）提供的公开数据集验证N-HiTS 模型。该数据集涵盖位于澳大利亚多种品牌、年龄、型号和配置的光伏电站输出功率及对应的温度、相对湿度、水平总辐射、水平散射辐射、风向、日降雨量、倾角辐射、倾角散射辐射等气象特征数据。采用位于澳大利亚爱丽丝泉的14 号光伏电站数据为本文数据集，该光伏电站由40 块额定功率为135 W 的光伏面板组成，总额定功率为5.4 kW。选取2021 年12 月至2023 年12月期间的数据进行实验，采样间隔为15 min，故文中涉及的相邻数据点间隔为15 min。假设所提供的气象特征数据为实际中能够准确预测的气象数据，为了提高光伏发电预测模型的准确性和可解释性，对数据集进行外生变量相关性分析以剔除对预测贡献有限的气象特征。根据表1 选取与光伏电站输出功率较相关的气象特征作为未来外生变量：水平总辐射、水平散射辐射、倾角辐射、倾角散射辐射。

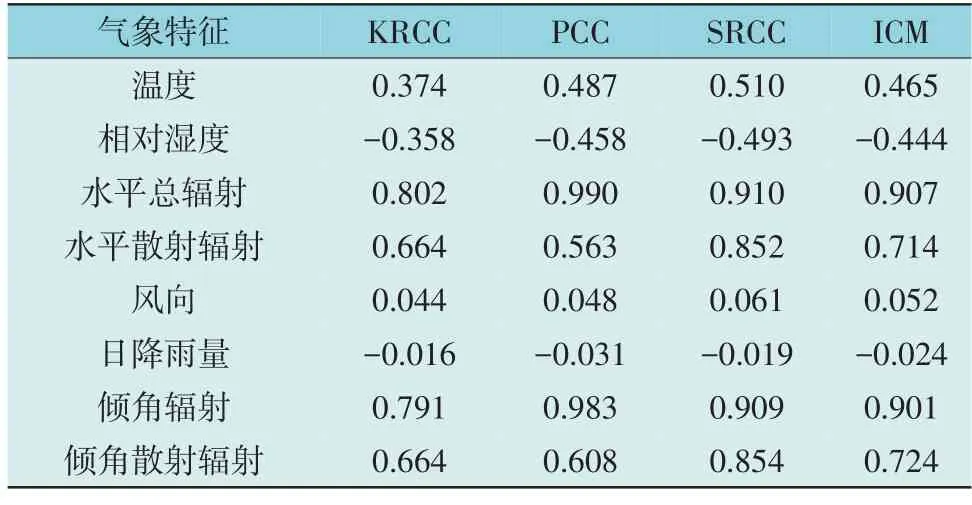
表1 气象特征与光伏电站输出功率的相关系数Table 1 Correlation coefficient between meteorological data and photovoltaic power output

3.2 实验设置

按8∶1∶1 的比例划分训练集、验证集和测试集，进行不同步数的光伏功率预测，采用式（24）对输出功率值和外生变量进行Min-Max 归一化处理：

式中：x为待归一化的数据；xmin为样本数据的最小值；xmax为样本数据的最大值；x′为经归一化的数据。

光伏出力预测流程如图3 所示，所用模型参数设置如表2 所示。

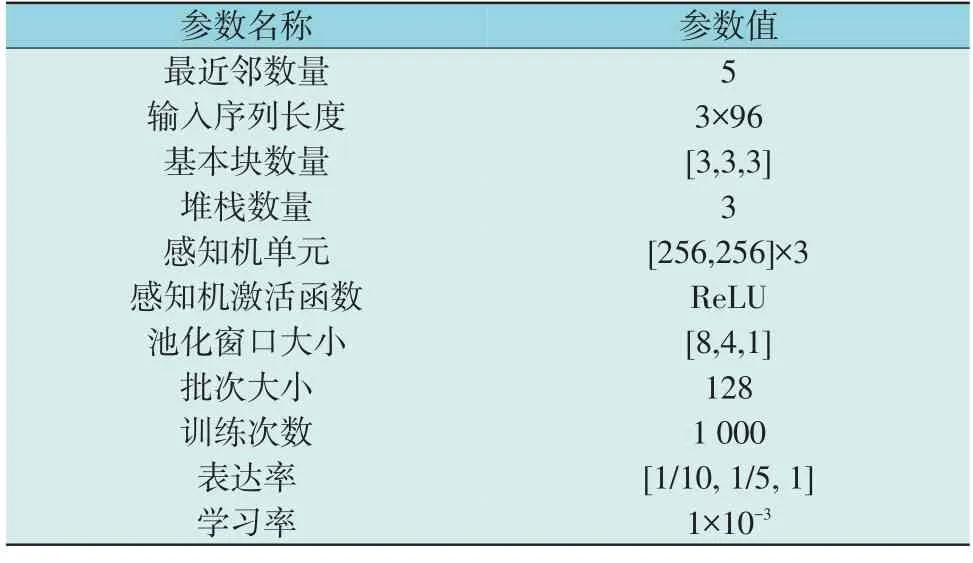
表2 模型参数Table 2 Parameters settings

图3 光伏预测流程图Fig.3 Flowchart of photovoltaic prediction

3.3 评估指标

采用均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）评估NHiTS 模型预测的性能，其量值分别为ERMS和EMA。RMSE 反映预测值与实际值之间的偏差程度，MAE 衡量预测误差的平均水平，这些评估指标可用于量化N-HiTS 模型在光伏出力预测中的准确性，计算公式为：

式中：M为预测样本的数量；ym为第m个预测样本的实际功率值；为第m个预测样本的模型预测值。

3.4 预测结果分析

为了检验本文数据处理方法的性能和其在长时间尺度预测上的适用性，分别对原始光伏数据采用不同的数据处理方法后经N-HiTS 模型进行预测步数为96 的预测。图4 为预测步数为96 时采用不同数据处理方法的预测结果，表3 为预测步数为96 时各数据处理方法的预测误差对比。

表3 各数据处理方法预测误差对比Table 3 Comparison of forecast errors of different data processing methods kW

图4 各数据处理方法的预测结果Fig.4 Prediction results of different data processing methods

由图4 和表3 可以看出，原始光伏数据经过本文所提数据处理方法可使得预测结果准确性更高，也说明了适当的数据处理有助于提高光伏发电功率预测的精确度。

为验证N-HiTS 模型的性能优势，选取光伏预测领域常用的TCN、门控循环单元（Gated Recurrent Unit，GRU）和LSTM 模型和N-HiTS 模型的原始模型NBEATSx 模型[30]、N-BEATS 模型[31]作为基线模型进行对比。将N-HiTS 模型与基线模型在数据集上分别进行超短期即0～4 h 时间尺度的多步预测，在15 min 的采样间隔下，4 h 内至多包含16 个预测步数。本文多步预测是指模型基于历史真实观测值，预测未来多个时间步长的输出，并不断滑动窗口，使用新的实际观测数据更新后续预测值进行评估，得到各模型预测精度如表4 所示。

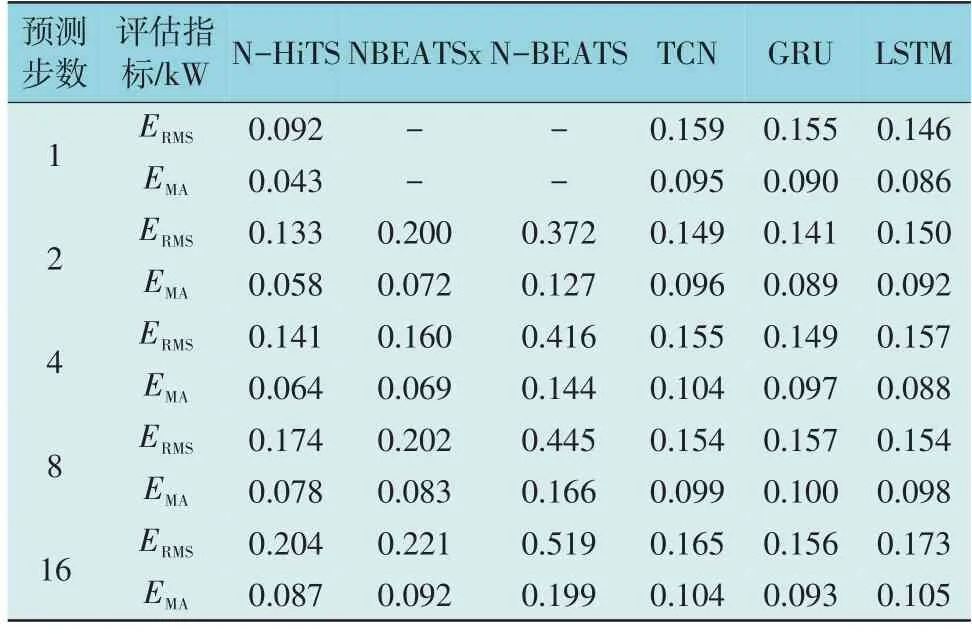
表4 不同预测模型的多步预测评估指标对比Table 4 Comparison of multi-step forecast evaluation indicators of different forecast models

由表4 可知，N-HiTS 模型的MAE 在超短期预测的所有步长均低于其他模型，这说明所提模型的预测准确度较高；然而在预测步长增大时，其RMSE表现略差于其他深度学习模型。这是由于RMSE对大误差更敏感，这说明所提模型在预测步长较大时可能产生较大的单个预测误差，例如未能提前捕捉到突变的气象条件，而是更多地根据历史数据规律给出预测结果。因此，N-HiTS 模型适用于对短期内有高准确性要求的预测场景，而在长期预测时可能需要结合其他方法来减少大误差的影响。一般情况下预测步数与预测精度呈负相关关系，即预测步数越大，预测精度越低。对于NBEATSx 模型和N-BEATS 模型而言，所采用的基函数为季节性和趋势性基函数，预测步数较小时效果较差，由表4 可看出，当预测步数为2 时，NBEATSx 模型和N-BEATS模型的预测精度较低，而当预测步数为4 时，预测精度较高。

为进一步评估N-HiTS 模型的性能，分析NHiTS 模型在平稳及动态变化条件下的准确性。图5 为预测步数为16 时N-HiTS 模型和基线模型分别在不同特征日的光伏功率预测结果，横坐标为预测点数，纵坐标为光伏功率。图5（a）为各模型在平稳日的预测结果，图5（b）为各模型在突变日的预测结果。

图5 预测步数为16时各模型光伏功率预测结果Fig.5 Photovaltaic power prediction result of each model when prediction step is 16

从图5 可以看出，N-HiTS 模型在光伏发电条件较为稳定的情况下具有较高的精确度，在可能面临多变的光伏发电条件的突变日中，N-HiTS 模型的预测曲线在大部分预测点上仍然能够紧跟实际功率曲线，但在功率上升和下降的转折点上，预测曲线与实际曲线之间出现了一定的偏离现象，在功率急剧变化的时段现象更为明显。这种现象反映出N-HiTS 模型在多步预测时虽然在变化的环境中保持了一定的预测准确性，但在应对快速变化的外部条件时，模型的适应性有待提高。

为展示N-HiTS 模型在解决长序列预测问题时的优越性，对各模型在不同回溯范围时的效果进行评估。图6 展示了预测步数为4 时各模型在不同回溯范围下的评估指标量值，可以看出，在较长的回溯范围下，尽管所有模型的误差有所增加，但NHiTS 模型的MAE 和RMSE 指标相对较低且增长趋势较为平缓，这表明N-HiTS 模型对于长序列预测问题具有较好的预测精度。

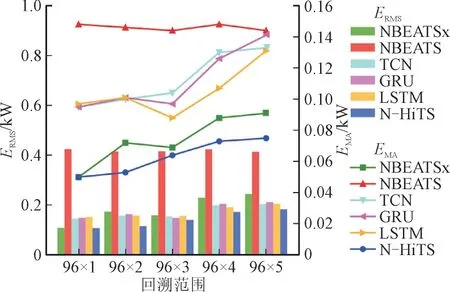
图6 预测步数为4时不同回溯范围下各模型效果对比Fig.6 Performance comparision of each model under different backtracking ranges when prediction step is 4

4 结语

面对全球能源结构转型和可再生能源发展的迫切需求，本研究提出了一种结合外生变量分析、数据质量控制以及基于N-HiTS 模型的光伏功率多步预测框架。在数据处理方面，提出了用于筛选外生变量的ICM 指标，通过合理运用外生变量和有效处理异常数据，增强了模型对复杂环境的适应性和鲁棒性。算例结果表明，N-HiTS 模型在光伏超短期多步预测中精度较高，处理长序列数据时具有较好的预测精度，但数据变异性的捕捉能力有限，未来需要进一步优化模型结构，提高其在数据动态性较强的长期预测任务中的预测准确性。本文所提的基于N-HiTS 模型的光伏功率预测框架有利于提高预测准确性和可靠性，对于优化能源结构、提高能源利用效率和电网稳定性具有重要意义。