考虑多变量相关性改进的风电场Transformer中长期预测模型

李士哲，王霄慧，刘 帅

（华北电力大学自动化系，河北保定 071003）

0 引言

近年来，随着我国风电行业的快速发展，风机装机容量逐年攀升，但由于风电消纳能力和电网电力运输能力不足，导致“弃风”现象频发[1-3]。随着电力市场交易的日趋完善，电力市场消纳风电的时机也逐渐成熟[4-7]。为了让风电与电力市场高度关联并满足现货电力交易的要求，需要对风电功率预测尺度和精准度提出更高要求。风电功率的中长期预测依赖于气象预报，但目前主要测重于季度的平均预测，这种预测在时间分辨率上远远不能满足风电交易业务的需求，因此需要实现更精细化的中长期预报。目前，虽然已有较多的风电功率短期预测和风电场多变量短期预测的研究[8-13]，但是针对风电场多变量中长期预测的研究仍然较少[14-15]。因此，对风电场多变量进行精细化中长期预测成为电力市场消纳风电的难题之一。

目前，对于风电场多变量预测有多种方法，文献[16]使用lightGBM 模型对风电功率进行数据清洗及异常数据修正，将处理后的风电功率输入Informer 模型进行短期功率预测，以得到更高的预测精度。文献[17]使用最优算法寻找最优网络参数，结合改进的机器学习模型对风电功率进行预测，虽然能够取得较好的预测结果，但遍历参数需要消耗较大的计算资源。近年来，深度学习模型被广泛运用在风电场多变量预测，例如长短期记忆网络（Long Short-term Memory，LSTM）[18-20]、门控循环单元（Gated Recurrent Unit，GRU）[21]、时域卷积网络（Temporal Convolutional Network，TCN）[22]。在这些深度学习模型中，由于循环神经网络能够较好捕捉时间序列中长期依赖关系和处理非线性数据，被广泛运用于风电功率的短期和超短期预测。但受限于循环神经网络的结构，无法对多变量数据进行并行运算，限制了对多变量数据的学习能力[23]。文献[24]提出的Transformer 模型具有优秀的数据并行计算和学习全局关系的能力，理论上更适用于多变量中长期预测任务。文献[25]在Transformer 模型中设计了特征提取层，加强了模型对多变量特征提取的能力。风电场多变量是复杂时变的时序数据，对其进行准确的中长期预测需要模型充分挖掘多变量间隐藏的相关性，但原始的Transformer 模型并没有跨变量的学习能力。

综上所述，本文针对Transformer 模型在捕获多变量间相关性方面的不足，提出考虑多变量相关性的多变量中长期预测模型。研究的创新在于：将输入序列的各变量通道切割成多个长度一样的序列片段并保留成单独通道输入模型，然后在时间维度和变量维度上对序列片段提取特征信息，通过序列合并的方式形成不同尺度数据，最后使模型学习到充分的特征信息。算例分析表明，本文所提模型能够在各个预测时长都能较好捕获风速未来的趋势并有效提高多变量预测的精度。

1 Transformer模型原理

Transformer 模型的结构主要由编码器-解码器组成。输入的历史序列首先经过词编码（Word Encoding，WE）和位置编码（Positional Encoding，PE），然后输入进编码器中。目标序列为解码器的输入。编码器-解码器由多个编码层和解码层堆叠组成，每个编码层和解码层都包含多个注意力和归一化等神经网络层[26]。为了便于理解公式中矩阵的含义，设定公式中矩阵对应着时间序列，矩阵的行对应时间序列的时长，列对应时间序列变量个数。Transformer 模型如图1 所示，图中将编码器提取历史序列的特征信息作为被查询向量K，V为内容向量，将解码器中目标序列经过归一化的输出作为查询向量Q。

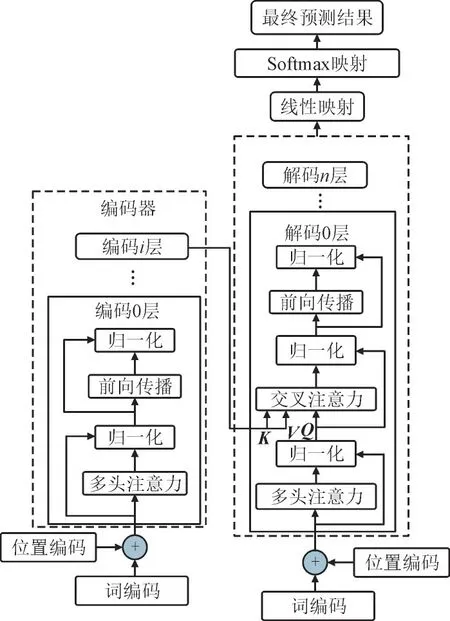
图1 Transformer模型Fig.1 Transformer model

1.1 词编码

词编码将输入序列中同一时刻所有变量的序列嵌入到1 个矩阵中，词编码维度即为列数的编号。其表达式为：

式中：s为词编码的输出矩阵；Ub(∙)为维度b的词编码函数；xt,D为行为t列为D的二维矩阵。

考虑输入序列中时间顺序，在词编码后加入了位置编码。位置编码主要是通过正余弦函数对输入序列进行编码，生成固定的位置矩阵来表示序列中的时间顺序，将s作为输入序列，则位置编码表达式为：

式中：P为位置编码矩阵；p为输入序列中时间顺序固定位置；u为输入序列的编号；ω为序列编号最大值；S为词编码和位置编码相加后的矩阵。

1.2 自注意力

Transformer 中的自注意力（Self-attention，SAT）模块能使模型在处理序列数据时动态地关注输入序列中不同位置的信息，以提高模型对输入序列数据的理解能力，其表达式为：

式中：A(∙)为注意力函数；a为输入序列的维度。

SAT 计算能使模型提取输入序列中每个位置对于序列整体的重要特征，从而使模型了解输入序列内部的规律，为模型预测提供丰富的特征信息。为提高SAT 学习输入序列中非线性规律的效率，对SAT 进行改进形成多头自注意力（Multi-head Self-attention，MSA）。MSA 将式3 中的Q，K，V，分成个多个等份矩阵放入不同的多头空间中并使用SAT 进行计算，再将不同头空间信息进行聚合得到更加丰富的数据。

1.3 编码器-解码器

Transformer 模型的编码器由图1 左侧的多个编码层堆叠组成，将词编码和位置编码相加的输出矩阵S作为编码层输入数据并且定义为编码i层内部第m个神经层的输出矩阵，每个编码层的表达式为：

式中：MMSA(∙)为多头自注意力函数；LLN(∙)为归一化函数；FFFW(∙)为前向传播函数。

Transformer 模型的解码器由图1 右边多个解码层堆叠组成，解码层的计算过程与编码层相比仅仅多了一个交叉注意力。通过交叉注意力将编码器提取的历史序列特征作为交叉注意力的K和V，将解码层中目标序列经过归一化的输出作为Q，以提供更加准确的上下文信息使解码器能够合理推断未来值。由式4 可推导交叉注意力表达式为：

2 Transformer多变量中长期预测模型

2.1 Transformer多变量中长期预测模型结构

Transformer 多变量中长期预测模型如图2 所示。其中，特征信息中不同颜色的长方体代表着不同变量的特征信息，长为时间序列的时长，宽为变量维度大小，高为词编码维度大小，二维概率稀疏注意力在编码层和解码层中。

图2 Transformer多变量中长期预测模型Fig.2 Transformer multivariate medium and long term forecasting model

2.2 多变量独立嵌入

对输入序列进行词编码实际上是将同一时刻内多个变量数据联合建模，这种建模策略是对输入序列中多变量关系的隐形挖掘，依赖于模型的神经网络对数据的反复学习。本文采用另一种建模策略，对多变量进行独立建模即多变量独立嵌入（Multi-variate Independent Embedding，MIE），此策略的优点是：将每个变量保留成独立通道，使模型对多变量关系进行显式挖掘，让模型更容易学习变量间的关系[27]。将行为Z列为D的二维矩阵YZ,D切割成J个形状一样的二维矩阵，多变量独立嵌入的表达式为：

2.3 二维概率稀疏注意力

在自注意力中需要将输入序列中的Q与K点积计算，但是每次计算便增加了计算复杂度O(LKLQ)的，O(∙)为复杂度函数（表示计算需要的时间与输入数据大小成线性关系），LQ，LK分别为Q和K的长度。文献[28]的研究发现：Q与K运算的数值分布具有稀疏性，选出Q中重要的数据可得到近似于Q中全部数据与K运算的效果。通过选取出新Q形成的概率稀疏注意力（Probabilistic Sparse Attention，PSA）不仅可降低SAT 的计算复杂度，而且提高了提取序列特征信息的效率，概率稀疏注意力表达式为：

为了提高计算的效率，将概率稀疏注意力改进成多头概率稀疏注意力（Multi-head Probabilistic Sparse Attention，MPSA）。Transformer 模型仅仅在时间维度上进行SAT 计算，忽略了变量维度的特征信息，因此，本文在时间维度和空间维度2 个维度分别进行MPSA 计算即二维概率稀疏注意力（Twodimensional Probability Sparse Attention，TPSA），如图3 所示。HL,d为一个行为L列为d的二维矩阵。Htime和Hdim分别为在时间维度和变量维度进行MPSA 信息提取后的矩阵。

图3 二维概率稀疏注意力Fig.3 Two-dimensional probability sparse attention

在多变量中长期预测中，为了提供充足的特征信息以保证精准预测，既要挖掘输入的历史序列上时间维度中隐藏的规律信息，又要关注历史序列中各变量之间的非线性关系。因此需要从时间维度和变量维度2 方面来进行MPSA 计算。二维概率稀疏注意力表达式为：

式中：W为Htime维度一致的随机矩阵；MMPSA(∙)为多头概率稀疏注意力函数。

2.4 多层式编码器-解码器

为了捕捉变量间不同尺寸的信息，本文模型结构采用了多层式编码器-解码器（Multilayer-style Encoder-Decoder，MED），其总结构如图2 所示。编码层将MIE 切割后的矩阵按照设定的合并窗口对相邻的矩阵进行合并形成多尺度数据，再经过编码层逐层学习。MED 结构是将每个编码层的输出结果不仅传递给下1 层的编码层，同时也输入到相应的解码层，最后模型将每个解码层的输出进行累加，通过线性映射和Softmax 映射得到预测值。单个编码-解码层结构如图4 所示。

图4 单个编码-解码层结构Fig.4 Structure of single encoder-decoder layer

由于Transformer 模型和本模型中神经层个数不一致，将本文模型中神经层个数用e表示。将记为编码i层中第e个神经层输出结果，编码层的计算过程表达式为：

式中：C[∙]为矩阵合并的函数；MTPSA(∙)为二维概率稀疏注意力函数；TMLP(∙)为多层感知机函数。

式中：G为一个二维的随机矩阵。

3 算例分析

3.1 数据集与评价指标

为验证本文所提模型的有效性，选取西班牙某地风电场4 年数据进行实验。数据包括风电场功率、风速等变量，以h 为单位进行采样。将总数据的70%作为训练数据，20%作为验证数据，10%作为测试数据。为帮助模型更好地学习数据，对数据集中缺失的数据和脏数据进行清理，并对每个变量进行了标准化处理，得到处理后的变量样本为：

式中：f为变量样本；为经过标准化处理的变量样本；μ为整个变量样本平均值；σ为整个变量样本标准差。

采用均方误差（Mean Square Error，MSE）和平均绝对误差（Mean Absolute Error，MAE）为模型预测准确度的评价指标，其物理量分别用EMS,EMA表示。EMS,EMA数值越小表明预测数值与真实数值的误差越小、预测精度越高。EMS,EMA表达式为：

3.2 对比模型

为充分验证本文模型的预测能力，选取循环网络LSTM 模型、Transformer 模型、Informer 模型作为对比模型，4 种模型参数设置如表1 所示。

表1 4种模型参数设置Table 1 Parameter settings of 4 models

3.3 对比实验

在对比实验中，LSTM 模型按照时间顺序迭代预测，Transformer 模型、Informer 模型和本文模型为一次性输出预测，例如当设定预测时长为48 h 时，本文模型会将48 h 的未来数据一次性输出。各预测时长下4 种模型的预测误差如表2 所示。

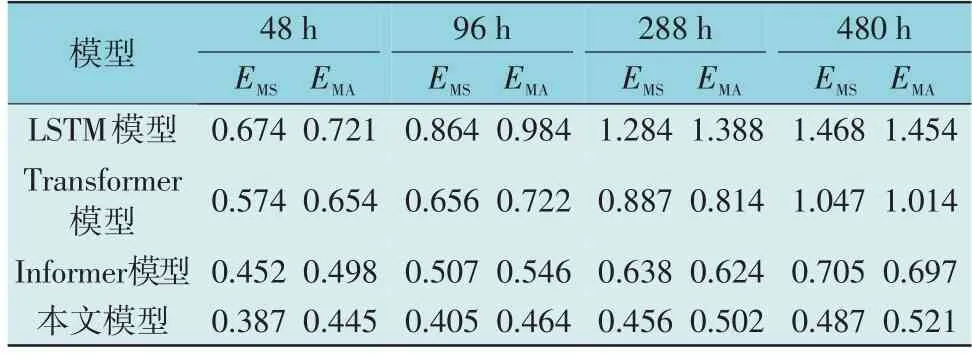
表2 各预测时长下4种模型的预测误差Table 2 Forecast errors of four models with different prediction duration

由表2 可知，当预测时长为48 h 时，本文模型与LSTM 模型相比EMS和EMA分别降低了42.58%，38.28%，与Transformer 模型和Informer 模型相比差距较小，这是因为在预测时长较少时，变量间的相关信息对预测效果并没有那么明显。当预测时长增长至480 h 时，本文模型与LSTM 模型相比EMS和EMA分别降低了66.83%，64.17%，与Transformer模型相比EMS和EMA分别降低了53.49%，48.62%，与Informer 模型相比EMS和EMA分别降低了30.92%，25.25%。当预测时长增长10 倍后，本文模型的EMS和EMA仅增长了25.84%，17.08%，LSTM 模型的EMS和EMA分别增长了117%，101.6%，Transformer 模型的EMS和EMA分别增长了82.4%，55.06%，Informer 模型的EMS和EMA分别增长了55.97%，39.96%。实验结果显示，本文模型与LSTM 模型、Transformer 模型、Informer 模型相比，均方误差在各不同预测时长分别降低了42.58%～66.83%，32.58%～53.49%，14.38%～30.92%。随着预测时长不断加倍本文模型的评价指标增长幅度也明显低于对比模型，表现出较高的预测精度和较好的鲁棒性。

在对比实验中，对48 h，96 h，288 h，480 h 4 种预测时长的风电功率进行比较，得到对应预测值与真实值对比曲线如图5 所示。从预测趋势上可知，本文模型能够在风电功率真实值的波峰波谷处密切跟踪风电功率趋势。

图5 不同预测时长下风电功率预测值与真实值Fig.5 Predicted and real value of wind power with different prediction duration

考虑风电参与电力市场交易的背景，对比不同预测时长下风电价格、风电场温度、风电场风速的预测值与真实值，如图6 所示。由图6 可知，对于风电价格和风电场温度而言，当预测时长为48 h，96 h 时能够精准捕捉风电价格和风电场温度的细微变化，当预测时长为288 h，480 h 时也能大致跟踪二者波谷的变化趋势。对于风电场风速而言，由于其随机波动性强，波峰波谷变化急剧，要完全拟合未来长期变化具有很大难度。尽管本文模型对于风速局部突变预测效果欠佳，但是本文模型的优势在于能够在各个预测时长都能较好捕获风速未来的趋势。

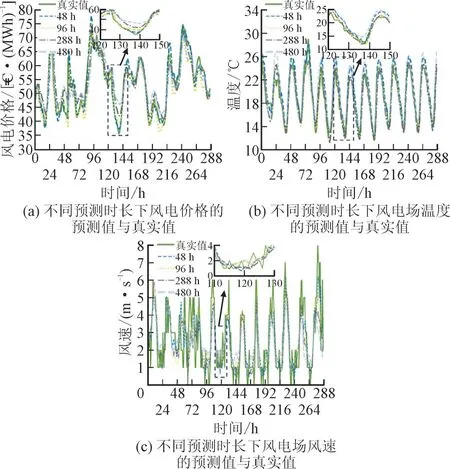
图6 不同预测时长下风电价格、风电场温度、风电场风速的预测值与真实值Fig.6 Predicted and real values of wind power prices，wind farm temperatures and wind speeds of wind farm under different prediction duration

3.4 消融实验

本文设计了MIE，TPSA，MED 这3 个消融组件来改进Transformer 模型，为了验证这3 个组件对提高多变量中长期预测精度和稳定性的影响，在消融实验中分别去除这3 个组件进行预测。以Transformer作为基线，MIE 为仅加入MIE 改进的Transformer 模型，MIE+MED 为加入MIE 和MED 改进的Transformer模型，MIE+TPSA 为加入MIE 和TPSA 改进的Transformer 模型，MIE+TPSA+MED 为未消融的本文模型。各消融组件在不同预测时长下的预测性能评估如图7 所示。

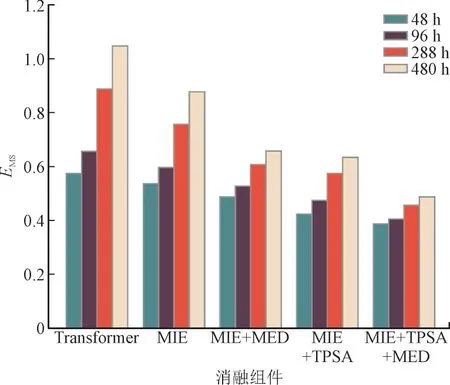
图7 各消融组件在不同预测时长下的预测性能评估Fig.7 Evaluation of predictive performance of various ablation components under different prediction duration

由图7 可知，加入MIE 消融组件的预测效果整体要优于Transformer 模型，这表明在处理风电场多变量预测时对各个变量进行独立建模是有效的。随着MED 组件的加入，预测时长从96 h 增长到288 h，其误差增幅小于加入MIE 消融组件和MIE+TPSA 消融组件的误差增幅，表明MED 组件在预测时长突增时能够有效保持模型的预测精度。MIE+TPSA 消融组件在各个预测时长的精度都优于MIE和MIE+MED 消融组件，这表明区别对待时间和变量维度进行注意力能够有效提高多变量预测的精度。

4 结语

本文针对Transformer 模型在捕获多变量间相关性方面的不足，提出考虑多变量相关性的多变量中长期预测模型。算例分析表明，本文模型与没有考虑多变量相关性的对比模型相比具有更高的中长期预测精度，更加适合风电场多变量中长期趋势的预测任务。但本文模型在风速波峰和波谷急剧变化时的预测效果不理想，在今后的研究中，需要增强模型对局部突变的感知能力，可考虑引入卷积神经网络来提高模型对短期内局部大幅变化场景的应对能力。