少齿差刚柔复合摆线减速器静态特性分析

黄思语，唐源，李晴朝，刘彦霆，唐健凯，吴昊

（中国核动力研究设计院核反应堆系统设计技术重点实验室，成都 610213）

0 引言

少齿差行星减速器有着尺寸小、减速比大、可靠性强、方便加工的优点，同时还具有运行稳定、受载能力高、振动小、传动效率高的运转优点，所以其在国防军事、医疗器械、航天航空等精密领域被广泛应用。吴素珍等[1]以自主研发的工业机器人关节减速器齿轮副为研究对象，考虑齿宽、齿隙和表面粗糙度等因素，采用有限元法分析不同工况下渐开线少齿差行星齿轮的接触应力应变，发现理论计算和有限元法的结果基本一致；Li[2]使用有限元方法研究了带有加工误差、组装误差、轮齿变形等因素的少齿差齿轮接触强度和弯曲强度问题；Chavadaki等[3]运用有限元法分析了两种FGM材料AISI4140合金和Ti6242S合金在不同齿根半径下的弯曲应力和变形，发现与根部半径为1.2 mm的Ti6242S合金相比，根部半径为1.2 mm的AISI4140合金的变形更小；Bekheet[4]对渐开线齿廓进行建模，并进行了应力和变形分析的有限元仿真，仿真结果与用AGMA弯曲和接触应力方程进行估算的结果比较，发现2D模型比3D模型更准确，同时材料的弹性模量对接触应力有很大影响；Chang[5]采用柔性齿轮转子驱动急回机构，研究了转子-机构耦合效应，采用有限元法和哈密顿方法建立系统模型，得到系统的动态响应并讨论了齿轮转子对急回机构三维振动的耦合作用；翟聪等[6]对一种新型少齿差行星减速器箱体受载情况进行静力学分析，改进后进行有限元模态分析，并对比分析了减速器的转频和啮合频率；黄伟等[7-9]分析了金属橡胶材料的力学性能，建立一对刚柔复合齿轮副的动力学模型及方程并进行动态特性分析，针对复合齿轮副进行振动性能验证，说明了加入耐高低温、抗腐蚀的金属橡胶材料后的复合齿轮副比金属齿轮副减速器齿轮传动中的振动冲击减小，传动更平稳，且传动效率也有所改善。

国内外学者对少齿差行星减速器及齿轮刚柔耦合模型均展开了大量研究，但是关于减速器齿轮副刚柔耦合有限元特性分析等方面还有一定的提升空间与研究价值，本文便针对这方面展开研究。

1 少齿差行星传动结构原理与传动特性分析

考虑到减速器尺寸大小与成本，为了压缩少齿差行星减速器的体积尺寸，将图1（a）所示传统双排双联齿轮结构改进换成如图1（b）所示的单排双联齿轮结构，该减速器主要传动部件包括输入偏心套、固定内齿圈（Z4）、行星轮也是双联齿轮（Z2、Z3）、行星架、输出轮（Z1）。改进后的偏心套筒与双联齿轮通过轴承连接，不影响其绕输出轴线公转，也不影响其自转。图1（b）中，内齿圈4固定，偏心轴套H输入，带动单排双联齿轮绕偏心轴的轴线转动，还和输入轴套一起绕着输出轴轴线回转，双联齿轮的内齿轮2带动输出小齿轮1输出运动，实现减速，双联齿轮3和固定内齿轮4在下方啮合时，输出齿轮1和双联齿轮2在上方啮合，二者之间的力可以相互抵消一部分，改善了减速器的受力情况，有效减少振动。

图1 少齿差减速器结构改进示意图

1.1 少齿差行星传动理论传动比计算

该NN型少齿差行星齿轮传动比可依据行星齿轮传动的方法计算（如图1（b）），双联齿轮2、3作为行星轮，既绕着偏心轴自转，还绕着输出轴公转，计算过程如下：

通用公式：

而

则：

得：

由于：

可得：

1.2 减速器传动原理

根据轴承和齿轮参数在MATLAB里画出复合摆线齿廓后，在SolidWorks里建立少齿差行星减速器三维装配模型如图2所示。

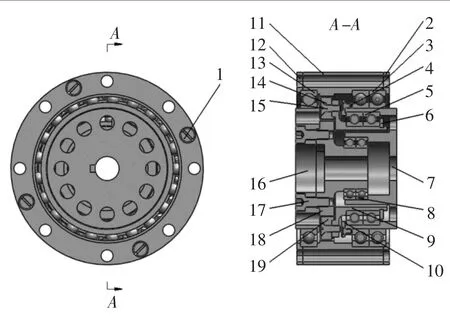
图2 新型少齿差复合摆线减速器示意图

输入端轴承3和输出端轴承13起支承内齿圈11也相当于机座的作用；偏心端轴承5在偏心套7上偏心安装，起支承偏心套作用，带动销轴套9公转，使通过开槽螺钉15固连的双联齿轮能够作偏心运动，既可以自转，同时绕输出端中心线公转。输出端16通过8个六角螺钉17与输出小齿轮18固连，开槽螺钉1固连输入端端盖2以及内齿圈11。当电动机带动偏心套绕机座中心转动时，偏心端轴承把偏心套的转动通过销轴套传递给固连的双联齿轮，而内齿圈11固定不动，所以双联齿轮绕输出轮轴线做偏心公转运动，同时双联齿轮绕偏心套中心所做的运动为反向自转运动。双联外齿轮与固定内齿圈这第一对齿轮副相啮合实现第一级传动，双联内齿轮与输出小齿轮这第二对齿轮副相啮合，完成第二级传动。

2 刚柔复合齿轮副有限元特性分析

2.1 聚氨酯弹性体弹性模量

聚氨酯作为一种有机高分子材料，其材料力学性能的可操作空间很大，控制结晶的刚性链段和不结晶的柔性链段的组成比例，聚氨酯弹性体就可以获得不一样的力学性能[10]，这决定了其具有良好的力学强度、耐磨损、耐高低温、承载能力大、辅助降噪、加工性能好、成本低、寿命长等优异性能。将其用于新型少齿差复合摆线双联齿轮副中，对于齿轮运转过程中吸振、减振有重要作用。

弹性体的力学参数中对齿轮副影响最大的就是弹性模量，氨基甲酸酯组成刚性链段，聚酯或聚醚组成柔性链段，它们的化学结构和物理性质的不同使这两者不能结合而形成微区结构[11-12]，可以通过改变微区结构性能来实现对弹性模量的变量控制，聚氨酯弹性体的弹性模量决定了在一定的负载下刚柔复合齿圈角度的转动量，为了建立有限元分析模型，需要对弹性体的弹性模量最小值进行分析。

根据徐涛等[13]的设计思路，将CSF-25减速器的扭转刚度作为聚氨酯弹性体变形量的计算条件。可以直接使用谐波减速器测试扭转刚度时的转矩与转角之比作为扭转刚度的参考值，查阅谐波减速器产品手册，CSF-25谐波减速器扭转刚度kg为1.2×104N·m/rad。

在双联齿轮之间填充8个间隔相同距离的完全一样的弹性体，如图3所示，通过其弹性变形吸收振动冲击并过滤掉噪声，同时可以传递一部分转矩，在双联齿轮间以及销轴上均设计间隙，使减速器齿轮在控制范围内能产生微小的浮动，双联齿轮上类似键槽的形状可以防止弹性体变形过大导致失效的情形，有效提高了新型减速器在不同工况的适用范围，避免在极端环境下的突发状况，如空转、卡死、卡顿等[14]。

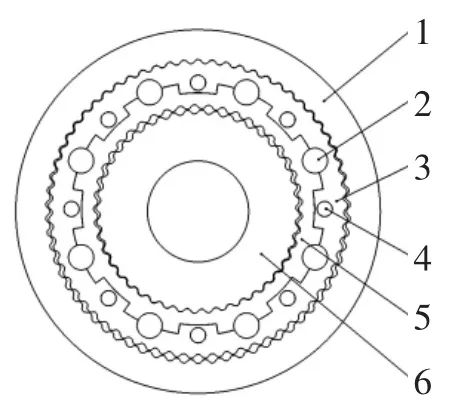
图3 少齿差行星减速器双联齿轮示意图

若齿轮1固定，齿轮3上施加60 N·m的转矩，聚氨酯弹性体会发生挤压变形与剪切变形，在这里可以假设均匀分布在双联齿轮上的8个弹性体在齿轮3和5之间受到的作用力是相等的。图4所示为其中一个弹性体受力变形示意图，当齿轮承受负载转矩时，负载力矩将使齿轮3和5对弹性体产生一对相反的作用力Fs，弹性体与齿轮3和5接触的部分会产生挤压造成压缩变形，在齿轮3和5之间间隙的剪切面处会产生剪切变形。

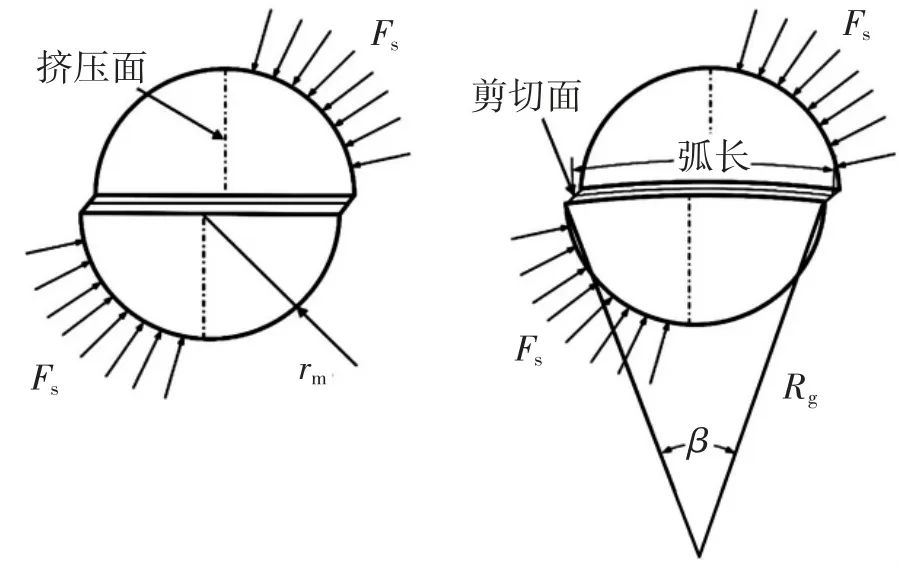
图4 圆柱弹性体受力示意图

Fs为在转矩作用下弹性体所受压力，rm为弹性体半径，Rg为齿轮中心到剪切面的半径，β为弹性体剪切面相对齿轮中心所对应的角度。则弹性体所受压力计算公式为

式中：n为弹性体在圆周方向的分布个数，T为转矩。

假设A1表示挤压等效压缩面的投影面积，计算公式为

其中，hR为弹性体的长度，根据几何关系可得：

弹性体的挤压应力可以表示为

剪切面面积计算如下：

式中，lR为弧形面长度，lR=βRg。

弹性体的剪切应力可以表示为

假设聚氨酯弹性体变形量较小，就可以根据连续介质力学，得到剪切面上的剪切应力γs为

式中：GM为剪切模量，GM=EM/[2（1+μM）]；EM为弹性模量；μM为泊松比。

基于圣维南定理[15]，在远离接触面的区域，挤压变形不明显，实际挤压应力比计算得到的σs小得多。假设弹性体的平均挤压应力为

式中：C1为比例因子，C1＜1。通过平均应力来对变形的弹性体应变能密度进行计算，可得挤压应变能密度和剪切应变能密度分别如下：

按照力学能量法，弹性体内存在的应变能与外力对其所作的功相当，则：

应变能为挤压应变能和剪切应变能之和，分别表示如下：

其中，V1为发生挤压变形的体积，可以看做弹性体的体积：

V2表示发生剪切变形的体积，由于其只作用于分界面的薄层也就是间隙处，故只占总体积的一小部分：

则可得：

弹性模量EM表达如下：

代入相关数值，求得聚氨酯弹性体最小弹性模量为39.7 MPa。

2.2 有限元模型建立

在SolidWorks中建立少齿差刚柔复合摆线齿轮副三维模型，将该模型转换为后缀是“.xt”的格式，在ANSYS Workbench中打开，先进行材料属性定义，在原有结构钢密度的基础上另外定义弹性体密度为1.26×10－6kg/mm3，弹性模量为62 MPa，泊松比为0.43。使用增广拉格朗日乘子法进行接触定义，与传统的拉格朗日法相比，增加了一个外点罚函数，可使求解时等式约束的乘子收敛速度更快，改善收敛性使收敛性更强。弹性体和双联齿轮之间定义为frictional，摩擦因数取0.25，法向接触刚度因子取0.1，齿轮副之间也定义为frictional，摩擦因数取0.1，法向接触刚度因子则取1。再进行网格划分，为减少网格划分数量，提高计算效率，齿轮副啮合面接触处网格尺寸定义为0.2 mm，弹性体以及双联齿轮间网格尺寸大小为0.4 mm，其余网格尺寸为0.7 mm，网格划分结果如图5所示。最后进行约束定义，内齿轮外圈固定，约束全部自由度，双联齿轮以及输出小齿轮定义远端位移约束，只有绕z轴的旋转自由度，其余5个自由度全部约束；全部弹性体由于与双联齿轮过盈配合，没有旋转自由度，加转矩后会发生变形，定义位移约束，仅约束z轴轴向位移；输出轮上施加力矩60 N·m，为了平衡在双联齿轮2上施加2.3 N·m的反方向力矩。

图5 刚柔复合摆线齿轮副有限元网格模型

分析弹性体半径Rt以及双联齿轮3和5体积变化，也就是齿轮3、5间分割之处半径Rc大小变化对齿轮副啮合轮齿应力及齿面接触力大小的影响，将齿面接触力在径向方向分力的大小作为减速器支承轴承所受的载荷。第一组改变弹性体体积尺寸，双联齿轮分割处半径大小为25 mm不变；第二组改变双联齿轮分割处半径大小，弹性体体积尺寸为第一组啮合应力最小的尺寸不变，如表1所示。

表1 有限元模型结构参数取值

2.3 不同弹性体半径的静力学特性分析结果

为了便于观察轮齿啮合最大应力情况，限于篇幅，在这里仅展示应力最大的双联齿轮5啮合处部分轮齿应力图，弹性体半径变化下的刚柔复合摆线齿轮副有限元模型求解结果如下。

图6所示为双联齿轮分割处半径取25 mm不变、弹性体半径Rt取值分别为1.9 mm至2.6 mm相应值时的应力图，分析齿面应力、齿面接触力变化。表2为改变弹性体半径有限元结果相关统计参数。

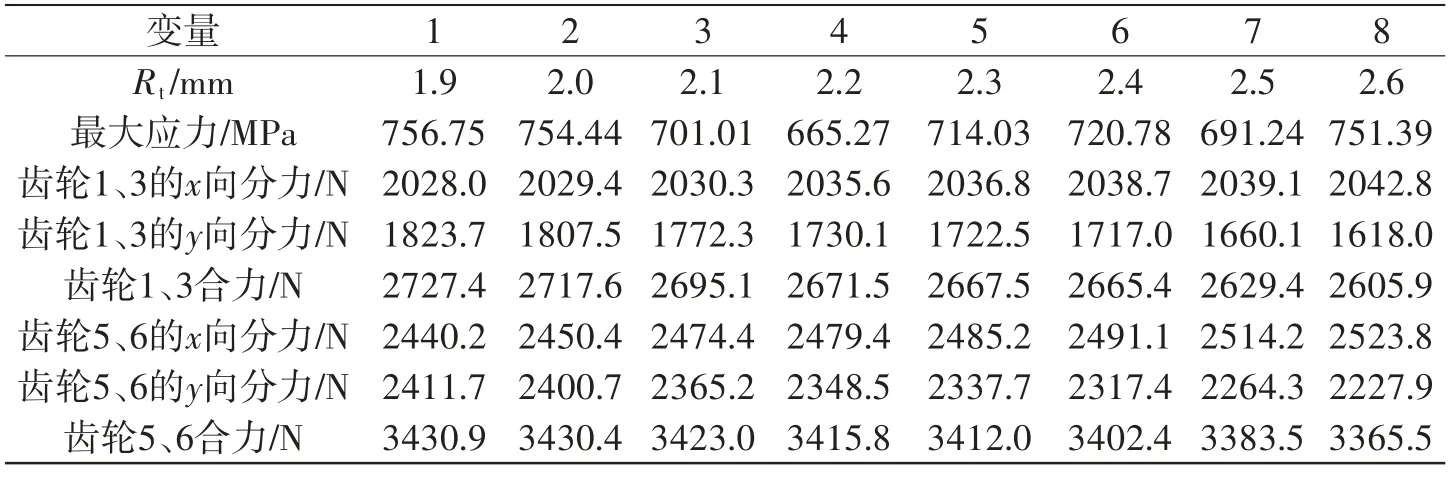
表2 以Rt为变量有限元结构模型结果

图6 改变弹性体半径双联齿轮齿应力图

根据表2数据可知，随着弹性体半径增加，双联齿轮5与输出小齿轮啮合部位轮齿最大应力整体呈先减小再增加的趋势，在Rt为2.2 mm时，应力最小为665.27 MPa；随着弹性体半径增加，双联齿轮3与内齿轮1接触力沿着x方向分力增加，齿轮传递载荷越大，接触力沿着y方向分力减小，支承轴承所受到的载荷越小，y方向分力减小幅度比x方向分力增加幅度大得多，所以总合力呈现减小趋势；双联齿轮5与输出轮6接触力沿着x方向分力增加，比齿轮1、3接触力沿着x方向分力增加幅度大，接触力沿着y方向分力减小，齿轮1、3接触力比齿轮5、6接触力沿着y方向分力减小幅度略大，y方向分力减小幅度比x方向分力增加幅度大，总合力呈现略微减小趋势，但是x、y方向分力以及合力均比齿轮1和3的相对应的接触分力、合力大，说明弹性体半径的增加一定程度上减少啮合冲击，减小齿轮副接触合力，并且对支承轴承所受载荷的影响大于齿轮间的传递载荷。

2.4 不同双联齿轮分割处半径的静力学特性分析结果

双联齿轮3、5分割处半径变化下的刚柔复合摆线齿轮副有限元模型求解结果如下。

图7所示为弹性体半径取2.2 mm不变、双联齿轮3、5分割处半径Rc取值分别为24.0～25.4 mm相应值时的应力图，分析齿面应力、齿面接触力变化。表3为改变双联齿轮3、5分割处半径有限元分析结果相关统计参数。

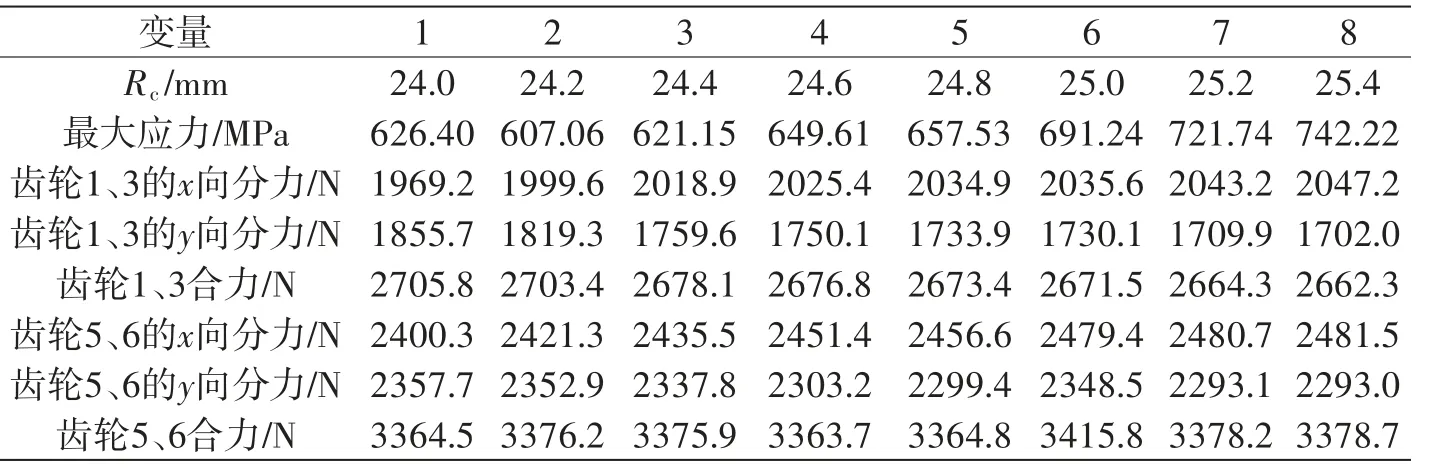
表3 以Rc为变量有限元结构模型结果

图7 改变双联齿切除处半径双联齿轮齿应力图

根据表3数据可知，随着双联齿轮3、5分割处半径增加，双联齿轮5与输出小齿轮啮合部位轮齿最大应力整体呈先减小再增加的趋势，在Rc为24.2 mm时，应力最小为607.06 MPa；随着分割处半径增加，双联齿轮3与内齿轮1接触力沿着x方向分力呈现增大趋势，齿轮传递载荷越大，接触力沿着y方向分力减小，支承轴承所受到的载荷越小，y方向分力减小幅度比x方向分力增加幅度大，总合力呈现减小趋势，x方向分力比改变弹性体半径的增加趋势大，y方向分力以及总合力比改变弹性体半径的减小趋势小；双联齿轮5与输出轮6接触力沿着x方向分力增加，与齿轮1、3接触力沿着x方向分力增加幅度相比变化不大，接触力沿着y方向分力呈现减小趋势，齿轮1、3接触力比齿轮5、6接触力沿着y方向分力减小幅度大，齿轮5、6总合力没有明显变化趋势，y方向分力比改变弹性体半径的减小趋势小，分割处半径的增加使双联齿轮3结构尺寸减小，齿轮5结构尺寸增加，说明双联齿轮3、5分割处半径的增加会减小齿轮3、内齿轮1间接触合力，并且对支承轴承所受载荷的影响大于齿轮间的传递载荷，对齿轮5及输出齿轮6间接触合力以及沿x、y方向分力影响不大。

3 结论

本文建立不同弹性体半径、双联齿轮分割处半径情况下的刚柔复合摆线齿轮副有限元分析模型，查看两者半径大小变化对轮齿啮合最大应力大小以及齿面接触力在径向、周向方向以及整体的接触力大小的影响规律，结果表明，弹性体半径为2.2 mm、双联齿轮分割处半径为24.2 mm时出现最大轮齿应力最小值。随着弹性体半径的增加，两对齿轮副接触合力均小幅减小，并且对支承轴承所受载荷的影响大于齿轮间的传递载荷；随着双联齿轮分割处半径的增加，双联齿轮3和内齿轮1间接触合力小幅减小，并且对支承轴承所受载荷的影响大于齿轮间的传递载荷，对输出轮6和双联齿轮5间接触合力以及沿x、y方向分力的影响不大。