基于余弦函数运动轨迹规划的算法研究

周鹏 李朋 陈胜华

宁波润华全芯微电子设备有限公司 浙江 宁波 315400

引言

在自动化设备运行过程中，快速、平稳、可靠、无碰撞是对控制策略的基本要求，控制策略的优劣对设备性能的发挥至关重要，它能体现整个设备的可靠程度和工业自动化水平的高低[1]。为了保证电机控制设备在启停过程中不产生冲击、超调、振荡等异常情况，在规划电机运行速度的时候需要加入专门的加减速控制策略算法来保证加减速过程中平稳精准的控制，这也是一个控制系统能否平稳运行，精准定位的前提保证。

传统的运动控制轨迹规划策略中常用的加减速控制算法包括梯形加减速算法、分段加减速算法、指数型加减速算法等，这些加减速方式在系统启动、停止和加减速开始和结束阶段存在加速度突变，加加速度会很大因而会产生冲击和异响，因此这些加减速方式不适合高速高精度的控制系统[2]。而常用的7段S型控制方法，虽然能够提供平滑的速度和加速度，但是其步骤较为烦琐、计算量比较大、对控制器的CPU性能要求比较高。本文提出了一种集成简易的“S”形加减速算法，其轨迹规划集成了简单的梯形加减速算法和余弦加减速算法，因三角函数在时间域内具有连续可导性，所以它具备了连续的加速度和加加速度，从而避免了其突变带来的冲击和振荡[3-4]。

1 传统加减速算法

在一些要求不高的场合一般使用梯形加减速或者指数型加减速算法，其中以步进电机控制最为常见。这两种算法的优点是运算量较小，算法实现简单，缺点是在加减速开始和结束、机器启动和停止阶段存在明显的机械冲击和振动。而余弦加减速算法相较而言比较复杂。

1.1 梯形加减速算法

梯形加减速算法是一种常用的运动规划算法，用于实现平稳的加速和减速过程，以达到稳定运动的目的。系统在加减速过程中，速度沿着固定的斜率变化，其加速度保持不变，如图1所示。

图1 梯形加减速速度变化示意图

由上图可知在定位过程中，速度变化分为加速、匀速、减速3个阶段。

在加速阶段，速度以固定的加速度上升，其速度如表达式（1）：

同理在减速阶段，速度以固定的加速度下降，其速度如表达式（2）：

经过分析加速开始和结束时刻，即上图中的O点和A点，加速度从0变为a和a变为0，即这一时刻的加加速度J为式（3）：

以加速度50mm/s，插值周期为0.002s为例，此刻的加加速度为25000mm/s2。这会导致在实际系统中出现电机的各种异响和振动，导致系统运行不够平稳。

1.2 余弦函数加减速算法

考虑到梯形加减速的缺点，以及余弦函数加减速的优点，本文考虑将两者结合，即在轨迹规划时候仍然使用梯形加减速规划的3个阶段，即加速阶段，匀速阶段、减速阶段[5-6]。在加速阶段、减速阶段的过程中引入余弦加减速算法。

二者结合后的速度规划示意图如图2所示。

图2 余弦加减速速度变化示意图

由图2可知，整体运动过程分为3个阶段，它们的耗时分别用t1、t2、t3表示。v0为规划的初始速度，vc为匀速运行的速度，ve为结束运行的速度。一般来说，定位时初始速度和结束速度都会设置为0。

根据上图描述，不同阶段的耗时、位移可以表述如式（4）所示：

其中，Sa、Sd、Sc分别表示加速阶段、减速阶段和匀速阶段的位移。

计算出3个阶段的执行时间和运行位移后，以时间t为自变量带入到余弦函数中，计算出3个不同阶段位移与时间的函数关系。

对处于不同阶段的位置函数求导可得到对应阶段的速度函数，如式（6）所示：

同理，对不同阶段的速度函数求导得到对应阶段的加速度函数，如式（7）所示：

由上式可知，不同阶段的加速度随着时间的变化而变化，并且在加速起始阶段、减速起始阶段，即t为0、t1、t3时刻，加速度是连续的[7]。正因为如此，采用余弦加减速在启停阶段不会存在加加速度突变的情况，对应的机械运动也不会存在冲击或异响。

该算法非常适合精确的定位控制，通过对不同阶段的位置函数进行积分运算可得到不同阶段的位移：

由（8）式可知，对位移积分后不同阶段的位移与梯形加减速完全一致，这样就大大简化了算法的运算量以实现目标控制。

2 算法的实现

结合上述的位置规划公式，在倍福TwinCAT的软件平台上实现该算法[8]。该算法主要分为两部分。算法流程图如图3所示。

图3 算法实现流程图

第一部分是根据设定的加速度、启停速度（默认为0）、运行位移（相对）来计算加速时间、减速时间、匀速时间（如果存在）、加减速位移、匀速位移等参数。第二部分是以时间为主线，随着时间的推移，设置不同运行阶段的给定目标位置[9]。

根据设定的加速度、位移等运动参数计算各个阶段的运行时间、位移是算法实现的重要组成部分。根据式（4）编写了该功能块，如图4所示：功能块中主要参数如表1所示：

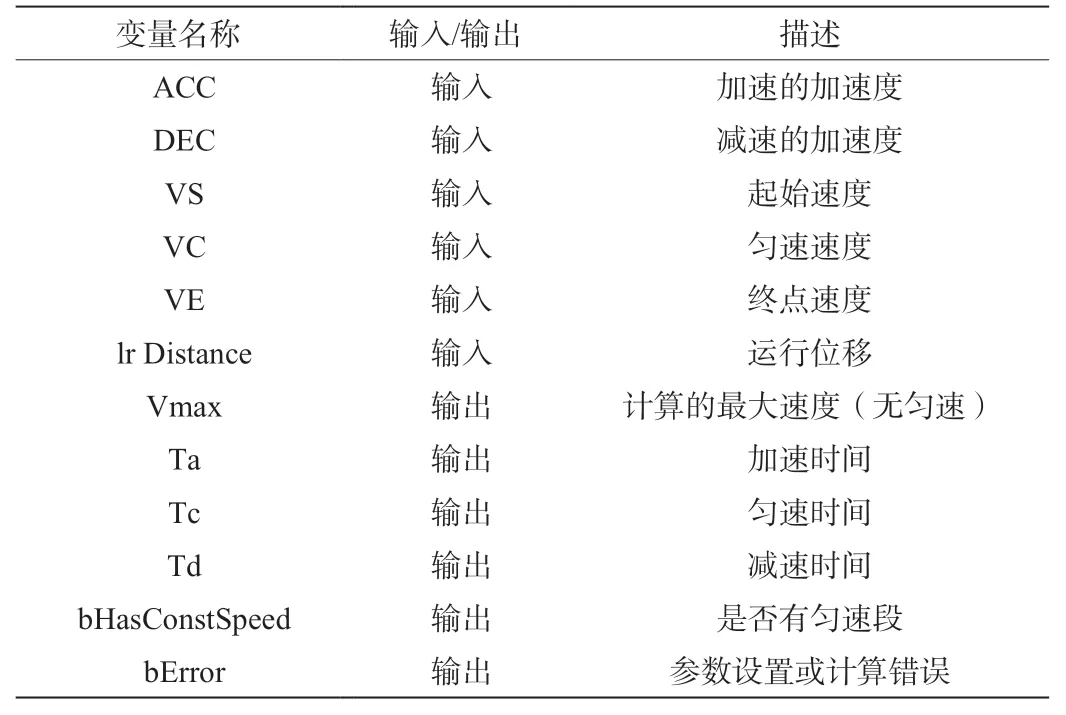
表1 轨迹参数计算关键参数

图4 轨迹参数计算功能块

图5 外部位置给定功能块

其中，是否有匀速段的判断至关重要。它将算法分为不同的两支，位置在不同阶段的给定也是不同的。在不同的阶段，根据式（5）可以得到不同时间阶段的位置给定。

3 算法的物理验证

在倍福的开发软件TwinCAT中编写的代码中，采用外部位置给定的功能来实现该功能[10]。

该功能块只需要配置对应的电机和实时（每个计算周期）给定规划位置即可控制电机按照规划的路径运行。设置ACC和DEC为50mm/s，Vs和Ve均设置为0。

实例1，设置匀速速度Vc为60mm/s，运行位移lr Distance为100mm。经过计算，加减速时间均为1.2s，加减速距离为36mm，且包含了匀速阶段。运动过程如图6所示。

图6 实例1运动轨迹

实例2，设置匀速速度Vc为60mm/s，运行位移lr Distance为40mm。经过计算，加减速时间均为0.894s，加减速距离为20mm，并不包含了匀速阶段,最高速度为44.7mm/s。运动过程如图7所示。

图7 实际运行结果波形

4 结论

本为提出了结合梯形加减速和余弦加减速的算法，能够在运动控制系统中按照运动要求，保证系统在加减速具有高度的柔性和稳定性。同时该算法折中考虑了运行的稳定性和算法的复杂程度，将该种算法在倍福的TwinCAT平台上做了验证，经过实验验证表明这一种加减速算法能够克服传统的算法的缺点来得到较为理想的速度和加速度。