基于大涡模拟的CAARC模型角区开槽气动优化研究

徐洲洋, 罗凯文, 杨 易

(华南理工大学 亚热带建筑科学国家重点实验室, 广州 510640)

风荷载往往是超高层建筑结构安全性和舒适性设计的控制荷载。且随着建筑高度增加,其横风向风致响应将逐渐超过顺风向响应。对建筑角区进行适当处理以来减小结构风效应,是超高层建筑抗风设计中常用的气动优化方法(图1)。

(a) 富力盈凯广场

(b) 云鼎大厦图1 采取角区处理的超高层建筑(图片源于网络)Fig.1 Super high-rise buildings with corner treatment (the images from the Internet)

风洞试验是早期研究方形建筑角区气动优化措施的主要方法。如Gu等[1]研究方柱圆角和切角措施下风荷载随角区尺寸的变化;严亚林等[2]研究了采用不同凹角率和切角率的方柱模型的气动特性;Li等[3]研究了10%的凹角率、切角率、圆角率对方柱的平均风压系数、基底弯矩、局部风荷载、功率谱密度和竖向相关系数的影响。Lu等[4]以方柱为对象,进行了12种角区修改模型的HFFB试验,研究角区修改对方柱基底荷载及顶部响应的影响规律。除方形建筑外,近年以CAARC标准建筑模型或矩形高层建筑为研究对象的相关研究开始增多。如庄翔等[5]研究了不同圆角率对矩形截面高层建筑表面风荷载特性的影响;董欣等[6]通过风洞测压试验和PIV试验探讨了圆角化处理对矩形高层建筑风荷载特性的影响机理。Li等[7]以CAARC模型为基础,分别研究了不同切角率、圆角率和锥度对其风荷载的影响。以上研究均表明,角区处理对高层建筑风荷载及响应有较好的优化效果。

在工程应用领域,谢壮宁等[8-9]以深圳京基金融中心等为例,探讨了顶部角区开敞和切角处理对结构风荷载及风致响应的影响;进而通过对广州西塔、深圳京基金融中心、天津高银117大楼的气动特性进行对比,发现117大楼具有相对最优的气动外形[10]。

近年来随着大涡模拟(large eddy simulation, LES)数值模拟仿真技术的进步,特别是入流湍流模拟精度的不断提高,研究者也开始采用LES开展高层建筑气动优化的研究。如Elshaer等[11]采用LES模拟加人工神经网络算法进行高层建筑角区优化研究;余远林等[12]以具有一定气动外形的南宁五象东盟塔为工程实例,进行了LES数值模拟和结构风振响应分析,同时进行了风洞测力试验,并将模拟结果与风洞测力试验进行对比,验证了数值模拟结果的准确性;罗凯文[13]使用LES研究了方柱采取不同角区开敞处理对模型基底弯矩和顶部位移响应的影响;Thordal等[14]利用LES方法研究了CAARC切角和圆角处理对结构风荷载与响应的影响,并将模拟结果与风洞试验进行比较,以验证数值模拟的精度。郑德乾等[15-16]以方柱为研究对象,探究采取角部优化措施对方柱本身及处于下游的方柱的影响,采用LES方法对时均和瞬态流场下的原型、倒角、切角模型周围流场及气动性能进行了模拟研究。结果表明,倒角和切角措施对方柱自身表面风压分布和气动力均有一定优化效果,也减弱了下游方柱的平均与脉动风荷载。

尽管当前采用数值模拟方法进行超高层建筑气动优化研究,以及应用NSRFG进行建筑风场绕流模拟的研究屡见报道,但结合二者开展高层建筑标模的气动优化系统研究的还相对较少。

本文基于CAARC标准高层建筑模型设计了4种开槽优化气动方案,采用作者团队提出的NSRFG (narrow-band synthesis random flow generation)入口湍流生成方法进行数值模拟比较研究。首先对NSRFG方法进行简要介绍和结合风洞试验进行验证,然后对4种方案进行建筑绕流模拟,通过比较基底弯矩和顶部位移、加速度响应以评价不同局部开槽气动优化措施的有效性。

1 大涡模拟入口湍流生成方法

入口湍流的准确模拟是进行结构风效应LES研究的前提,也是目前计算风工程研究的热点问题。LES入口湍流生成方法可分为预前模拟数据库法、循环法和湍流合成法[17],其中湍流合成法[18]是目前的主流方法。近年来,不同的LES入流湍流方法被提出,如DSRFG方法[19]、CDRFG方法[20]等。

Yu等[21]基于脉动风速时程的单点窄带过程的模拟和叠加,提出了可严格保证入口湍流满足连续性等条件的NSRFG方法,提高了数值模拟的计算精度和效率,相对于DSRFG和CDRFG方法,NSRFG方法的脉动风速表达式相对更加简洁,有效提高了LES入口湍流生成的计算效率和湍流风场的数值模拟精度,在计算风工程领域得到较多引用[22-25]。

NSRFG方法中,模拟入流脉动风速场的数学表达式为

(1)

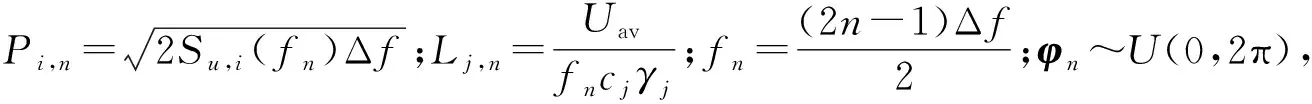
当kj,n满足下列方程组时,所生成的湍流速度场为无源场,满足大气边界层的湍流特性要求

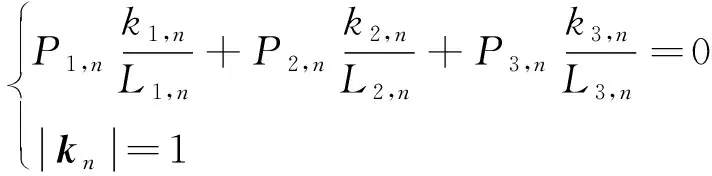
(2)

式(2)使得无源场的条件得到满足。根据空间解析几何,向量kj,n的各个分量可由下式求解

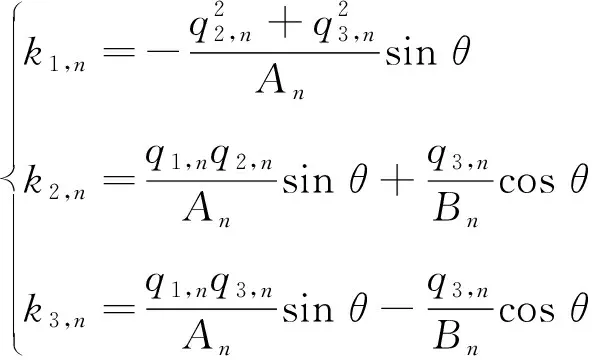
(3)

2 CAARC数值模拟

在进行气动优化模拟研究之前,先采用NSRFG方法对CAARC原始模型进行建筑绕流模拟计算,将计算结果与风洞试验进行对比,以检验数值模拟的精度,验证其适用性。

2.1 风洞试验概况

在华南理工大学风洞实验室开展了CAARC标模的刚性模型高频压力积分测压(HFPI)和高频动态天平测力(HFFB)试验,如图2所示。CAARC标模原型尺寸为45.72 m×30.48 m×182.88 m,缩尺比取1∶300。参考高度取模型顶部高度,参考高度处的风速为11.1 m/s。采用挡板、尖劈和粗糙元来模拟我国GB 50009—2012《建筑结构荷载规范》中对应的C类风场。测压模型共布置7层140个测压点,测点布置见图2。

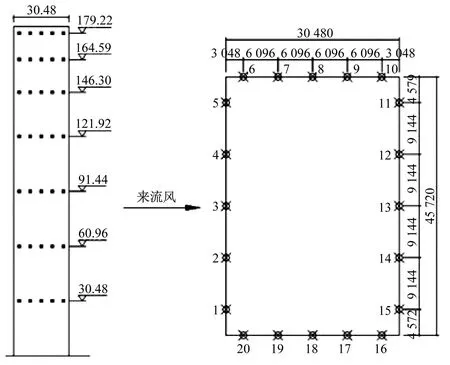
图2 CAARC标模风洞试验及测点布置Fig.2 Wind tunnel test of CAARC standard model and pressure taps configuration

2.2 数值模拟

2.2.1 参数设置

数值模拟基于CFD商用软件ANSYS FLUENT平台进行,采用用户自定义程序(UDF)二次开发功能将NSRFG方法嵌入以生成湍流风场作为LES模拟的入流边界条件。入流湍流模拟中,空间相关参数取值与文献[21]保持一致。所采用的计算域及边界条件如图3所示,数值风洞模型采用1∶300的缩尺比,阻塞率为0.4%<3%,满足建筑绕流要求。数值模拟中参考高度和参考风速与风洞试验设置相同,计算时长为16 s,时间步长为0.002 s。数值模拟收敛标准设为10-5,数值求解格式如表1所示。

图3 计算域及边界条件Fig.3 Computational domain and boundary conditions

表1 大涡模拟求解格式Tab.1 Solution formats in large eddy simulation

2.2.2 空域验证

在进行CAARC标模绕流计算之前,参考文献[12],首先进行了空域湍流边界层风场的模拟验证,以检验平衡态大气边界的模拟满足要求。算例中对应的速度、湍流强度特性剖面的定义满足规范规定的C类地貌要求。算例对应空域的风场特性模拟结果如图4所示。结果表明,速度剖面和湍流强度剖面与规范吻合较好。此外,模型顶部处的脉动风速功率密度在低频部分与Karman谱吻合较好,在高频处发生衰减,这与大涡模拟的滤波作用有关。总体而言,该数值模拟的风场能够满足建筑绕流的条件。

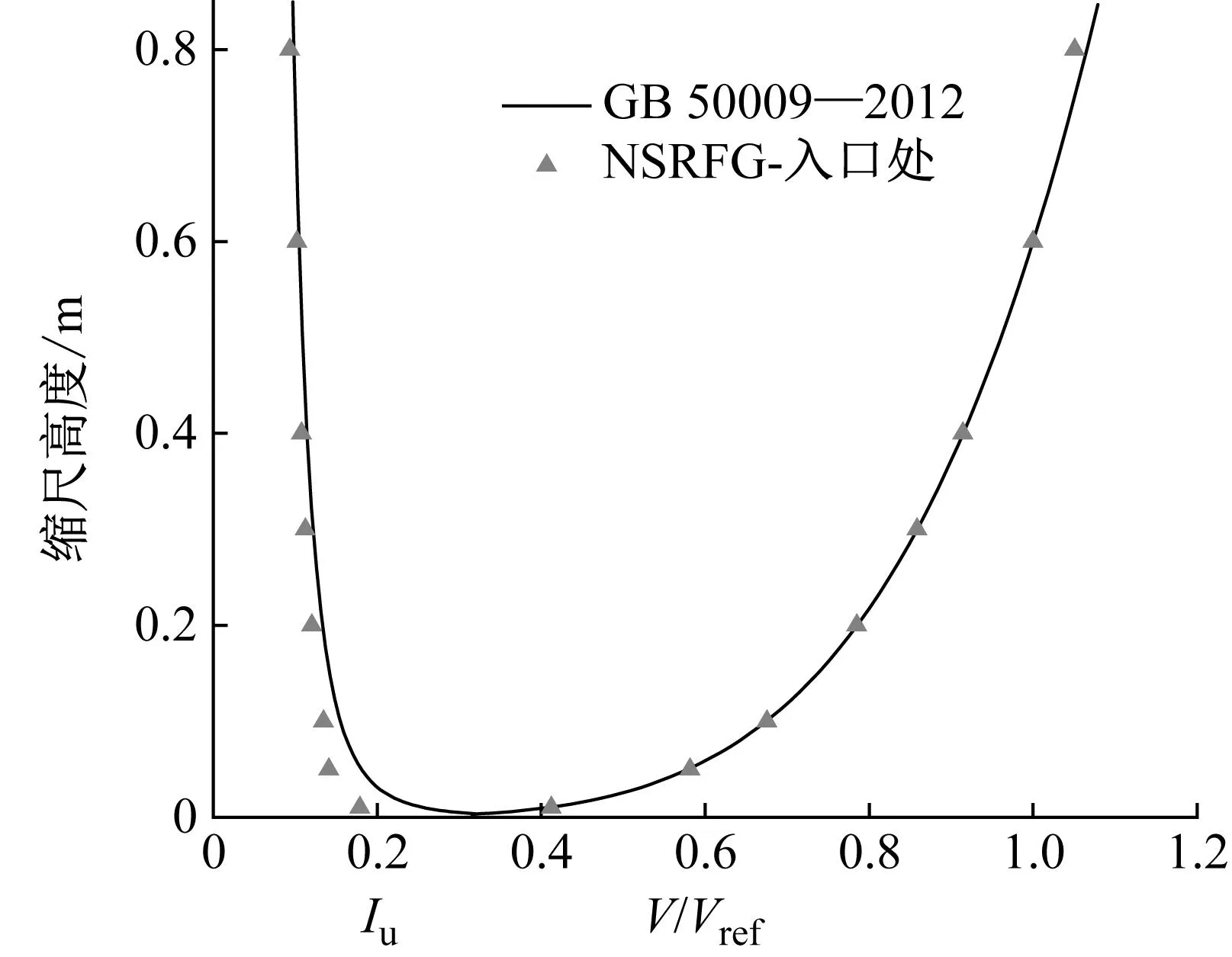
(a) 湍流度剖面及平均风速剖面

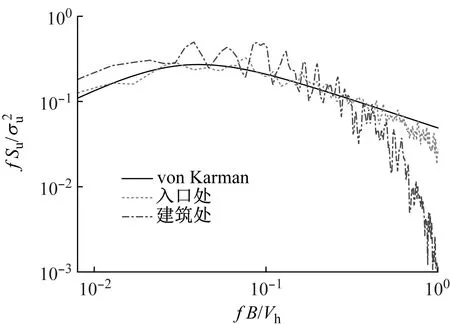
(b) 参考高度处脉风速功率谱图4 风场特性模拟结果Fig.4 Simulation results of wind field characteristics

2.3 结果分析

2.3.1 风压系数定义

根据JGJ/T 388—2014《建筑工程风洞试验方法标准》,对CAARC标模2H/3处的压力测点进行分析。以未受干扰的模型顶部高度处来流风压作为参考,测点风压系数定义为

(4)

测点的平均和脉动风压系数分别定义为

(5)

(6)

式中:Cp(k)为某测点在样本点k的风压系数;p(k)为测点在样本点k的瞬时风压值;p∞为静压值;ρ为空气质量密度;Vh为建筑顶部高度处的来流风速;N1为总样本点数。

图5给出了2H/3处CAARC模型表面平均风压系数与脉动风压系数的风洞试验与数值模拟结果。对于平均风压系数,由NSRFG方法得到的各测点的平均风压系数与风洞试验结果吻合较好;而对于脉动风压系数,采用NSRFG方法得到的各测点脉动风压系数总体与风洞试验结果规律一致,数值稍大。整体看,NSRFG方法模拟的精度满足要求,为后续采用数值模拟方法进行气动优化研究奠定基础。

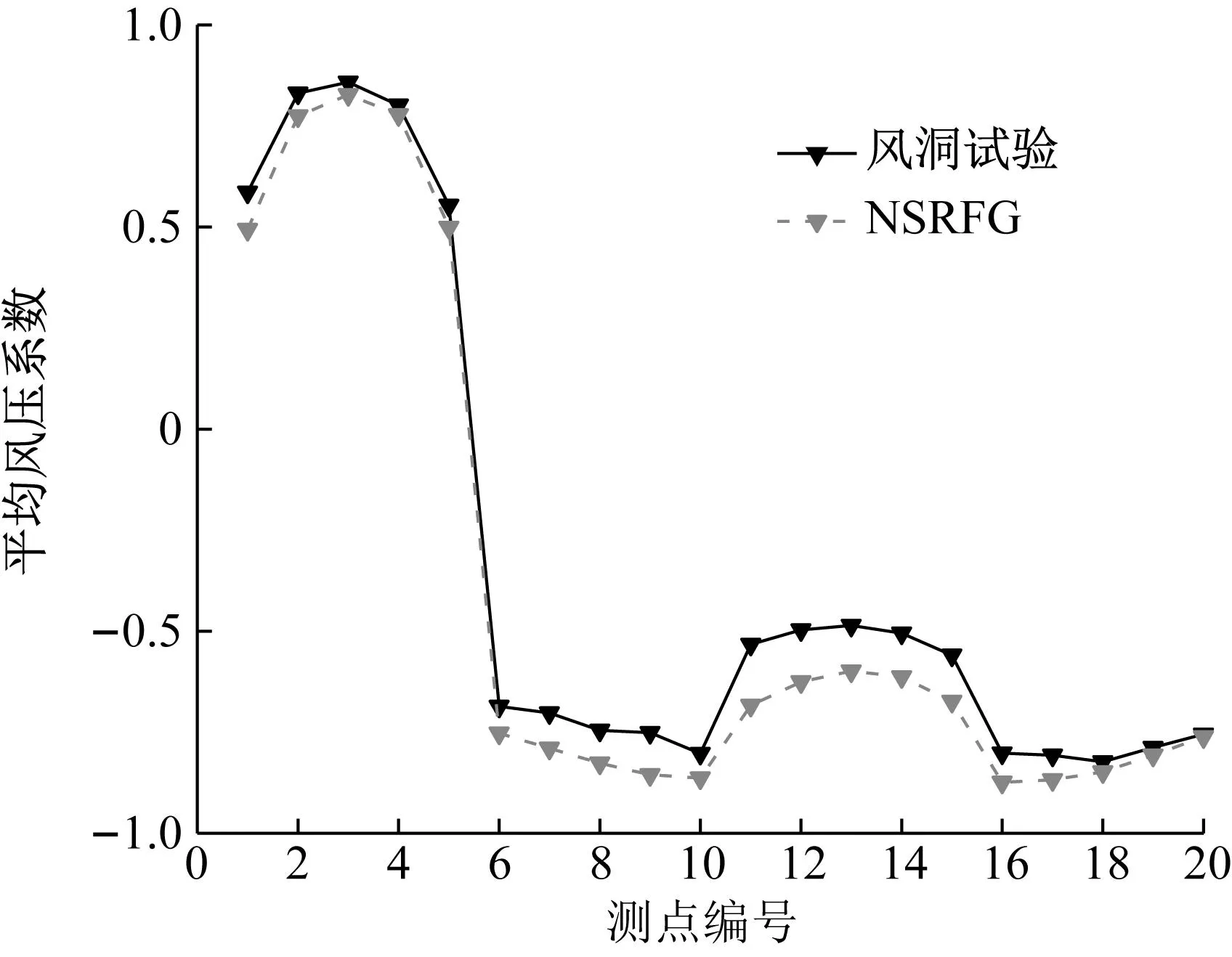
(a) 平均风压系数

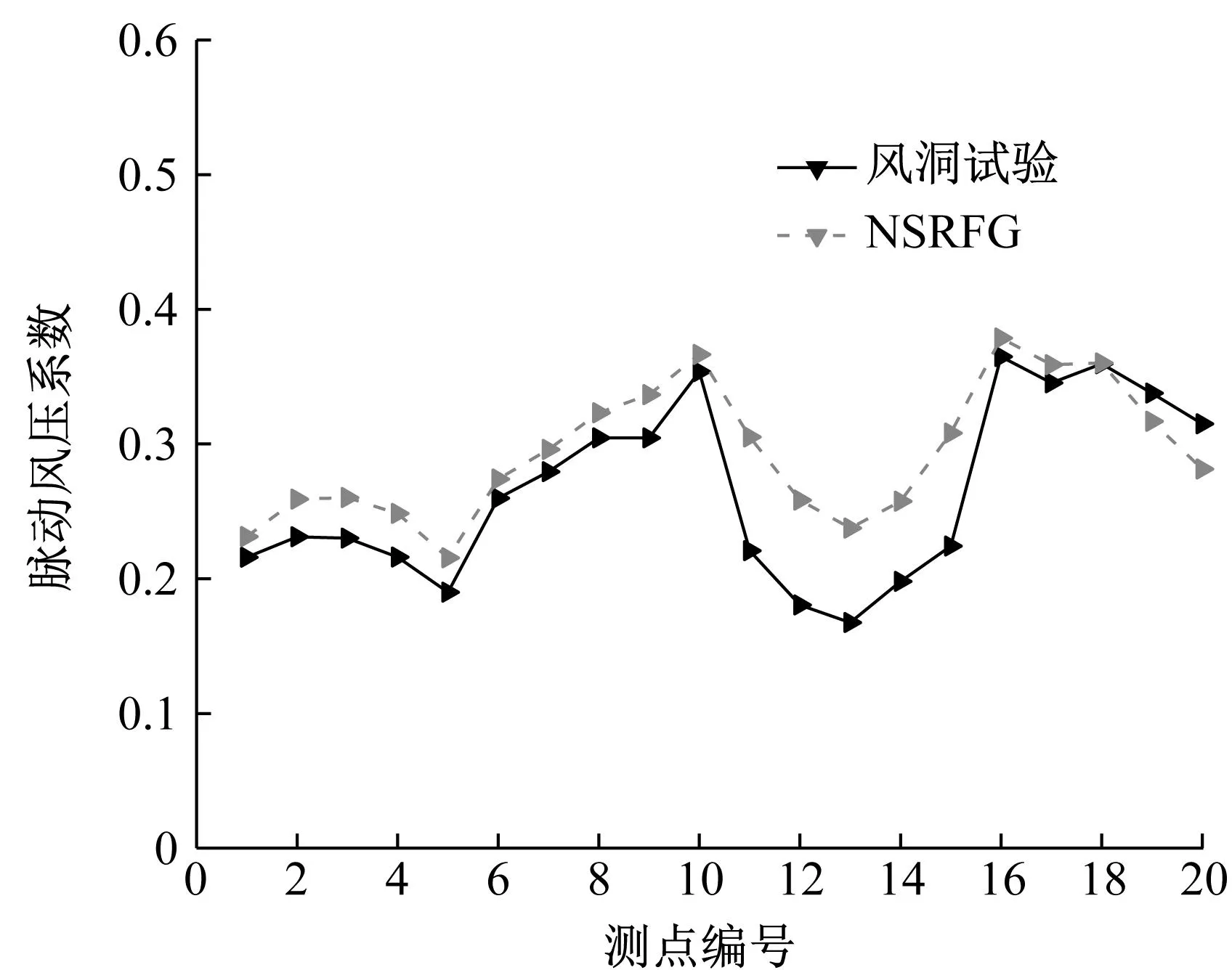
(b) 脉动风压系数图5 CAARC平均风压系数和脉动风压系数Fig.5 Mean pressure coefficient and fluctuating pressure coefficient of CAARC model

2.3.2 基底弯矩系数

对基底弯矩做归一化处理,使用弯矩系数对风洞试验与数值模拟结果进行对比。定义顺风向、横风向及扭转向基底弯矩系数分别为

(7)

(8)

(9)

式中:Vh为参考高度处的风速;B和D分别为CAARC模型的顺风向和横风向宽度;H为模型高度。其归一化的弯矩系数功率谱如图6所示。结果表明,通过风洞试验得到的CAARC基底弯矩功率谱与使用NSRFG方法模拟得到的基底弯矩功率谱虽有一定的差异但总体上吻合度较好,验证了数值模拟的可靠性和适用性。

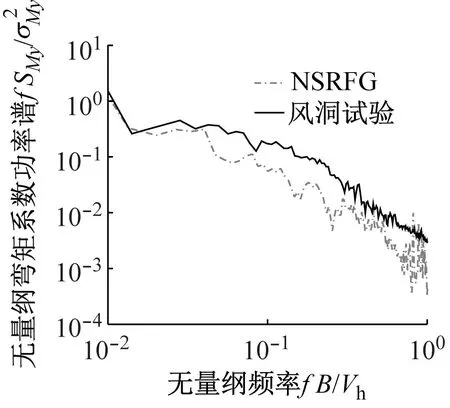
(a) 顺风向

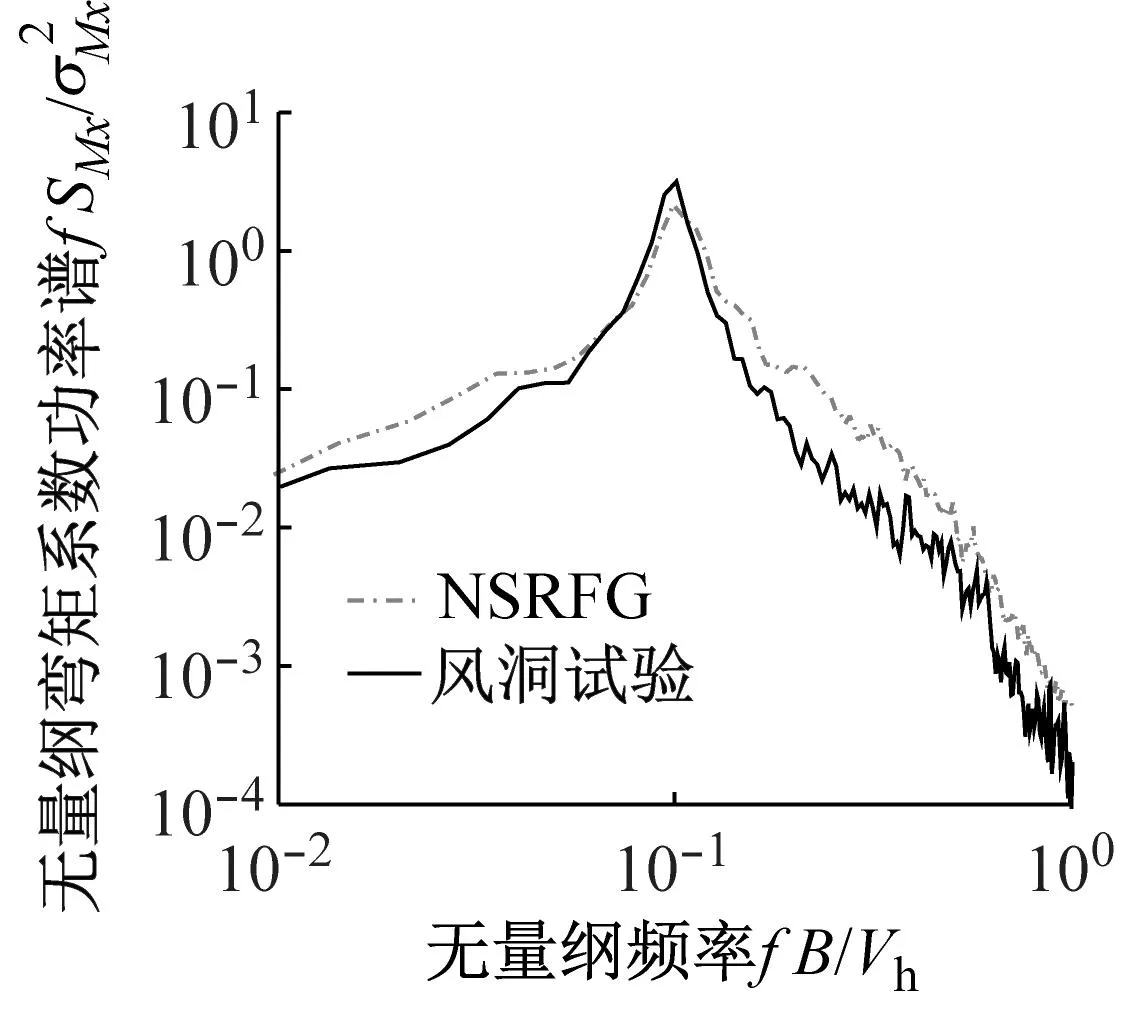
(b) 横风向

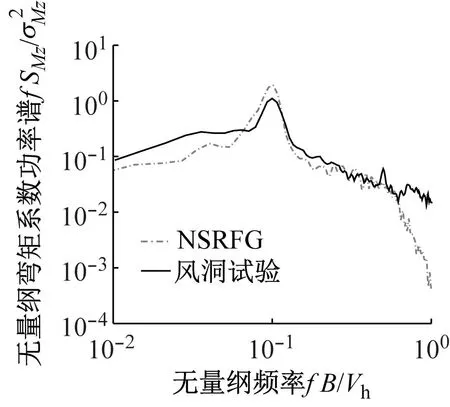
(c) 扭转向图6 CAARC基底弯矩系数功率谱Fig.6 Power spectrum of base moment coefficient for CAARC model

3 模型概况

本文在文献[13]对方柱角区局部开槽优化的研究基础上,在CAARC模型三个高度处(1/2H、2/3H、5/6H)进行角区、单边和周向开槽处理,共计5种模型,如图7所示(图中B=152.4 mm,D=101.6 mm,H=609.6 mm,d=15 mm),以研究不同局部开槽措施下的气动特性。为便于描述,将CAARC原型、角区开槽、顺风向开槽、横风向开槽、周向开槽分别称作模型1～模型5。

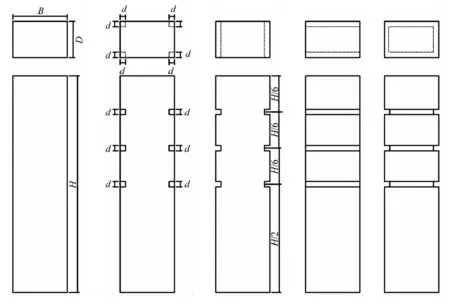
图7 CAARC模型角区气动优化方案示意图Fig.7 Schematic diagram of the corner aerodynamic optimization scheme of CAARC model

4 数值模拟

建立了与4种角区气动优化方案相对应的数值风洞模型。LES模拟中,时间步长均取为0.002 s,计算时长16 s,取后14 s的时程数据进行计算分析,该采样时间换算到原型约为800 s。优化模型中计算域及边界条件与CAARC原型保持一致,几何建模与网格划分采用内外域相结合的方式。图8给出了5种数值风洞模型的内域网格划分图,其中模型最小网格尺寸为1 mm,增长率为1.05～1.10,各模型体网格总体数量介于573万～776万之间。

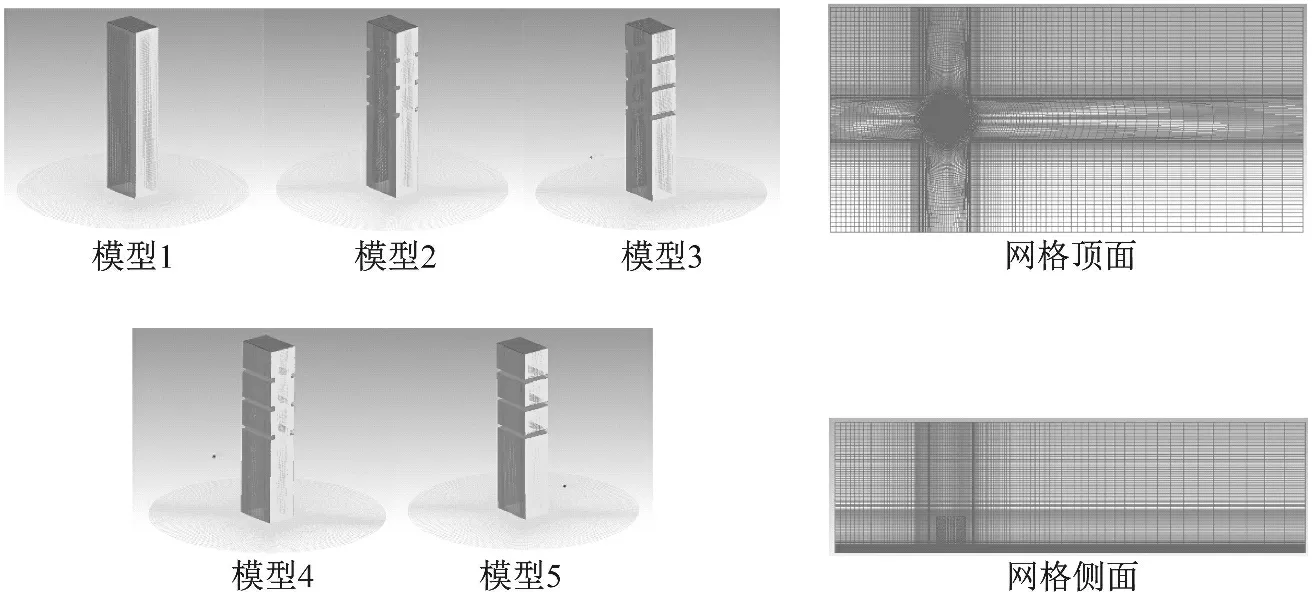
图8 模型网格划分Fig.8 Computational grids for model

5 结果分析与讨论

5.1 基底弯矩系数功率谱

图9给出了数值模拟得到的5种气动优化方案的CAARC模型的基底弯矩系数功率谱密度,结果表明:

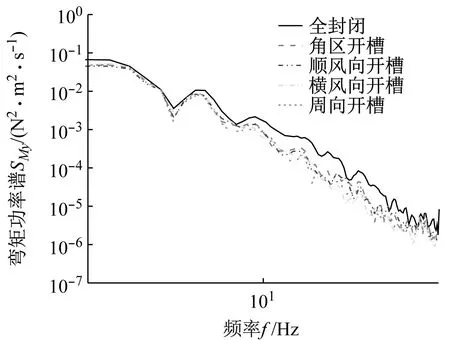
(a) 顺风向

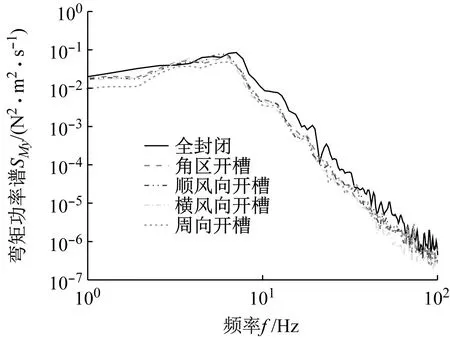
(b) 横风向图9 各方案基底弯矩系数功率谱密度比较Fig.9 Comparison of the power spectrum density of the base moment coefficients for each scheme

(1) 整体来看,在较宽的频率范围(2～30 Hz)内,横风向基底气动弯矩功率谱密度值远大于顺风向,表明模型横风向风致响应超过顺风向。横风向基底弯矩系数功率谱值在6～7 Hz左右出现峰值,与CAARC模型的横风向漩涡脱落频率一致。

(2) 对于顺风向,与全封闭原型相比,采取开槽处理后4种角区优化模型的顺风向基底弯矩系数功率谱值均出现不同程度的降低。在低频处(f<0.5 Hz),4种模型的减小幅度均较小;而当f>0.5 Hz,减小幅度均明显增大,说明4种优化方案均有效削弱了顺风向气动荷载。横向比较,4种方案之间的优化效果差异较小,相对而言,周向开槽在较宽的频带内谱能量下降幅度相对更大,对顺风向气动荷载削弱效果更明显。

(3) 对于横风向,与全封闭原型相比,采取开槽处理后的模型横风向基底弯矩系数功率谱值也均出现不同程度的降低。同时,功率谱的峰值均有所降低,漩涡脱落频率略微向低频段移动。在达到模型的漩涡脱落频率之前,周向开槽相比其他方案对于谱能量的削减程度更大,而在达到漩涡脱落频率之后,4种方案之间的削弱效果未呈现明显差异。整体而言,周向开槽对于谱能量的削减效果更好。

5.2 结构顶部位移及峰值加速度

根据基底弯矩功率谱密度并结合结构动力参数,采用频域法估算建筑顶部位移响应。参考Braun等[26]的做法,假定振型沿高度呈线性分布,结构前两阶模态固有频率均假定为0.2 Hz,阻尼比设为1%。根据《建筑结构荷载规范》,假设建筑模型位于广州市,则50年一遇基本风压为0.6 kPa,峰值因子g设为2.5,CAARC模型的密度设为160 kg/m3。

基于以上假定,高层建筑的平均位移响应可按下式估算

(10)

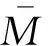
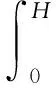
(11)

(12)

结构顶部的峰值加速度响应可按下式进行估算

(13)

通过计算得到各模型的顶部位移响应及顶部峰值加速度响应,由于横风向平均位移接近于零,故不给出横风向平均位移结果。5种方案的顺风向平均位移、脉动位移和横风向脉动位移及顶部峰值加速度分别如图10、图11所示。

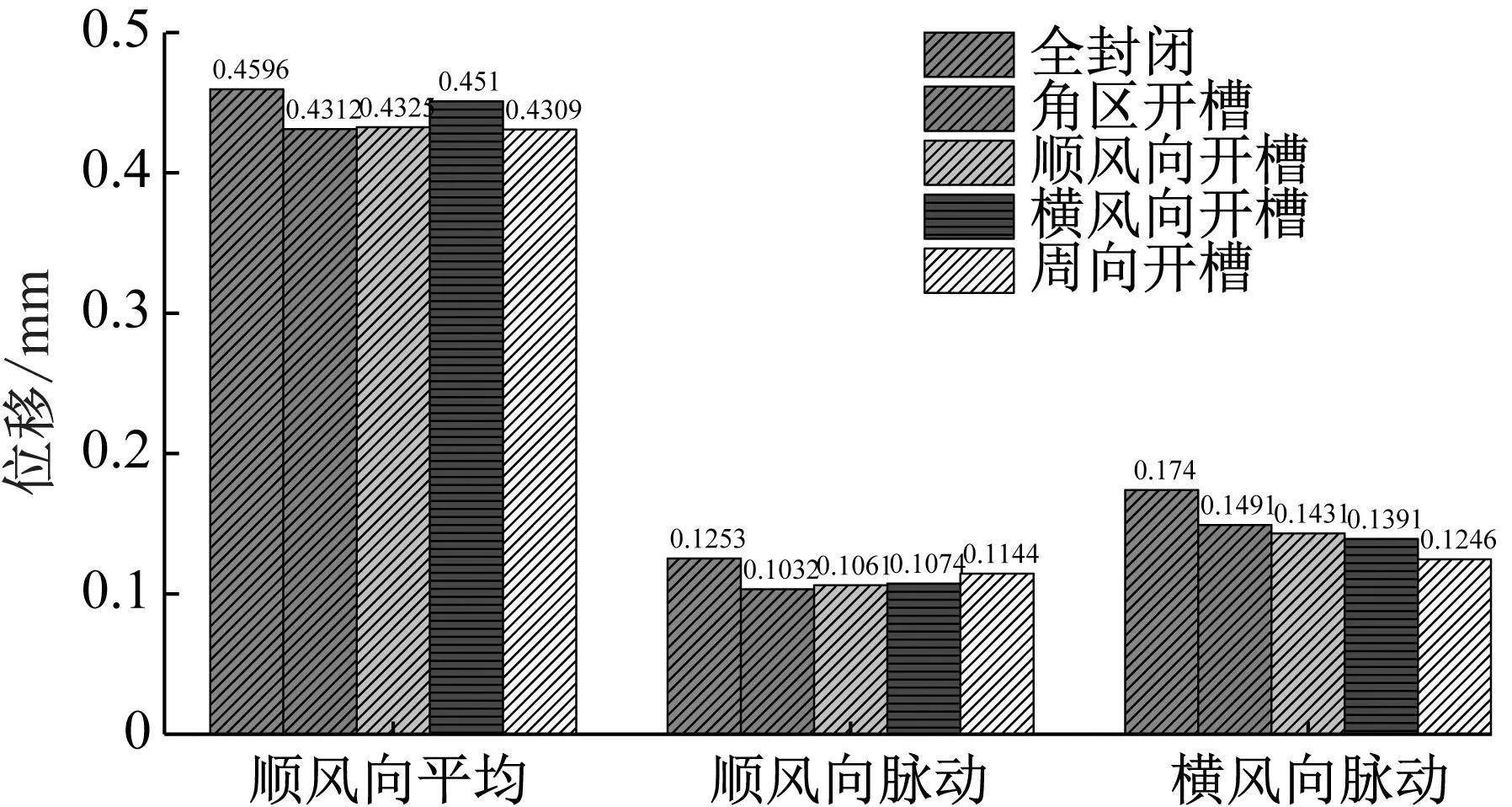
图10 各方案顶部位移响应Fig.10 Top displacement response of each scheme

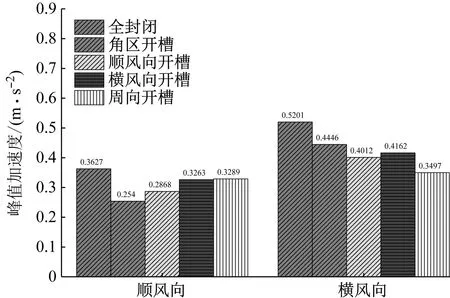
图11 各方案顶部峰值加速度响应Fig.11 Top peak acceleration response for each scheme

由图10可知,模型顶部顺风向平均位移整体比顺风向脉动位移大,横风向脉动位移整体也比顺风向脉动位移大,采取开槽方案能使CAARC模型的顶部位移响应在一定程度上有所降低。对于顺风向平均位移,相比于模型1,模型2～模型5分别降低了6.2%、5.9%、1.9%、6.2%;对于顺风向脉动位移,相比于模型1,模型2～5分别降低了17.6%、15.3%、14.3%、8.7%;对于横风向脉动位移,相比于模型1,模型2～5分别降低了14.3%、17.8%、20.1%、28.4%。

由图11可知,模型顶部横风向峰值加速度整体比顺风向峰值加速度大,说明模型的横风向加速度响应已经超过顺风向。采取开槽方案使模型顶部峰值加速度出现明显降低。对于顺风向峰值加速度,相比于模型1,模型2～5分别降低了30%、20.9%、10%、9.3%;对于横风向峰值加速度,相比于模型1,模型2～5分别降低了14.5%、22.9%、20%、32.8%。

图10和图11的结果表明,CAARC的横风向脉动位移响应和峰值加速度响应已经超过顺风向,模型2～5整体上对于横风向响应的优化效果比顺风向响应的优化效果更好,且对于加速度响应的优化效果整体上也比脉动位移的优化效果更好。整体上采取开槽方案后,相比于模型1,模型2～5对于顺风向平均位移响应优化效果较小,但对于顺风向和横风向脉动位移响应及峰值加速度响应优化效果较为显著。其中,模型2对于顺风向脉动位移和顺风向顶部峰值加速度优化效果最好,模型5对于横风向脉动位移和横风向顶部峰值加速度优化效果最好,从减小高层建筑横风向响应角度考虑,建议采用周向开槽方案。

5.3 流场分析

以模型1与模型5为例,给出2/3H高度截面处前16 s的时均速度大小云图与16 s时刻的瞬时速度大小云图以及模型周围流场分布,如图12所示。对比12(a)和图(b)可看出,模型5两侧的漩涡基本消失。而横风向漩涡脱落是造成结构横风向风致振动的主要原因。经过流动分离后,形成的尾流区域变大,模型后方的一对分离涡与建筑模型存在一定距离。对比图12(c)与图(d)也可看出,周向开槽模型两侧漩涡的生成得到了明显抑制,漩涡尺寸变小。模型尾流区域呈现出无规则的气流运动,说明在周向开槽范围内,漩涡脱落的规律性和连续性被破坏,从而影响结构的横风向风致响应。

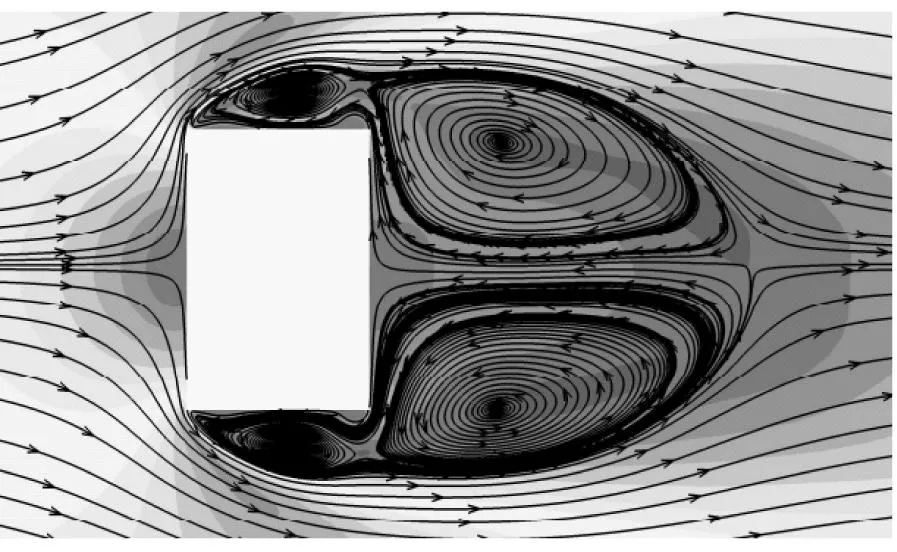
(a) 模型1平均速度云图

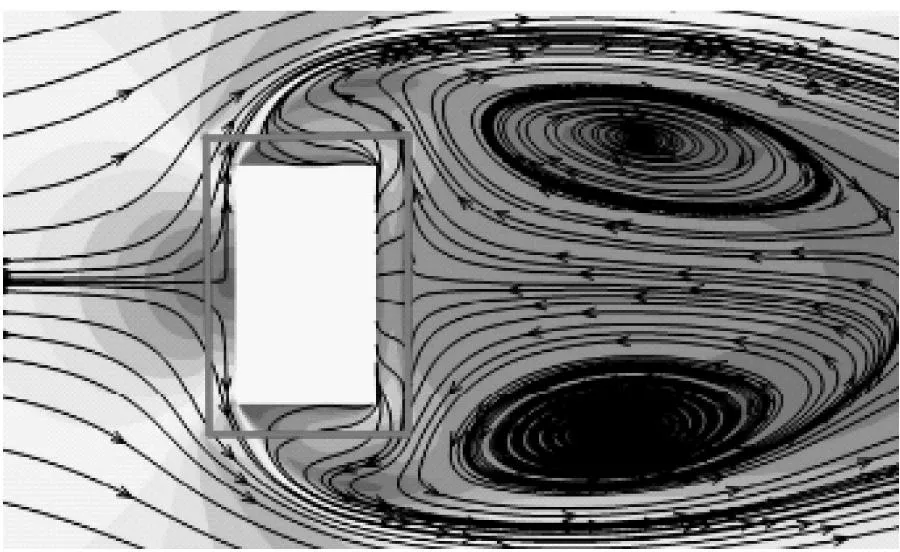
(b) 模型5平均速度云图

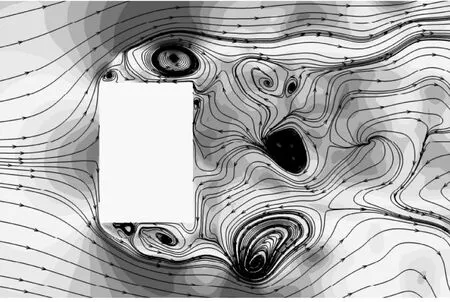
(c) 模型1瞬时速度云图

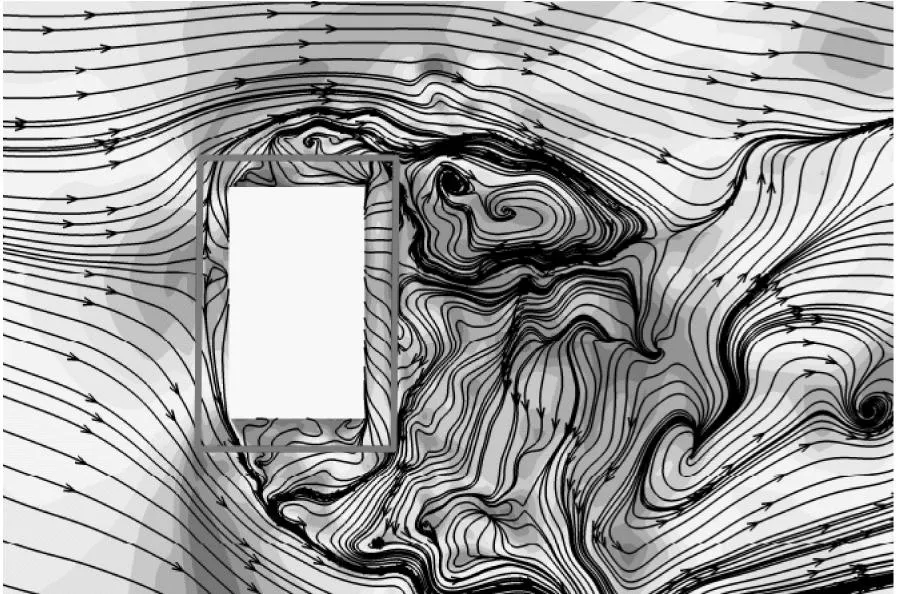
(d) 模型5瞬时速度云图图12 模型速度大小云图和流线分布Fig.12 Velocity contour and streamline distribution of the model

6 结 论

本文以CAARC建筑模型为基础,考虑了4种局部气动方案,并采用作者团队提出的NSRFG方法进行LES研究,利用模拟得到的基底弯矩和顶部位移进行对比分析,得到的主要结论如下:

(1) 与全封闭原型相比,采取不同开槽方案均能降低顺风向和横风向响应。整体上顺风向响应的优化效果按由强到弱的顺序为:角区开槽、顺风向开槽、横风向开槽、周向开槽,横风向响应的优化效果按由强到弱的顺序则为:周向开槽、横风向开槽、顺风向开槽、角区开槽。

(2) 采取开槽方案对于横风向响应的优化效果更加明显,其中周向开槽能使横风向脉动位移响应和横风向峰值加速度响应分别降低28.4%、32.8%,从减小横风向响应的角度考虑,周向开槽是4种开槽方案中的最优方案。未来将结合风洞试验方法对气动优化措施的效果进行进一步验证。