直升机抗坠毁元件构形设计分析研究

卢致龙

(中国直升机设计研究所,江西 景德镇 333000)

提高抗坠性能是直升机安全技术发展中的重要目标[1],波纹梁作为直升机在抗坠毁设计中较常使用的结构之一,是一种典型的抗坠毁吸能元件;复合材料波纹梁整体成型质量较好,相对于复合材料加筋壁板结构适合大尺寸一体化成型,可设计成结构梁形式参与机身传力,同时方便与周边结构安装连接,在直升机坠毁触地后可起压溃吸能的作用,具有良好的应用价值;对波纹梁设计技术的研究有助于提高直升机整体的抗坠毁设计水平。

Bannerman等[2-4]研究了多种形式的直升机抗坠毁元件结构,以及Shanahan等[5]所著的直升机坠毁统计报告记录了20世纪80年代多型直升机的坠毁事故调查结果,反映了如军用直升机AH-64阿帕奇直升机纵向两侧主梁采用波纹梁结构,获得了一定的能量吸收能力。

刘瑞同等[6-8]通过试验及数值仿真方法研究了复合材料波纹梁的吸能特性,孟祥吉等[9]对不同铺层波纹梁吸能性能进行研究分析其破坏过程,蒋宏勇等[10-11]对波纹梁耐撞性进行了研究。Sokolinsky等[12-13]对波纹梁进行准静态压溃试验及Kindervater等[14-15]对不同结构形式的复合材料结构进行比吸能试验研究表明了复合材料波纹梁的几何参数对其吸能能力的影响不一。但以往研究大多基于某种特定波纹梁构形以及针对薄弱环节设置开展的试验及数值仿真研究,对复合材料波纹梁波纹段形状参数,及构形参数关联性影响波纹梁吸能能力及性能表现的研究较少。本文结合工程实际,针对直升机设计工程中使用较多的波纹梁结构研究其波纹段形状规则,差异化构形参数,分析其对波纹梁坠撞冲击吸能的影响;本文研究的波纹梁结构可布置在驾驶舱地板底部,当直升机坠毁触地后起压溃吸能保护乘员的作用,研究结果有助于提升直升机抗坠撞设计能力。

1 波纹梁结构设计和理论分析

波纹梁波形为类三角函数波形,对波纹形梁结构设计主要是基于波形尺寸、波纹腹板圆角以及薄弱环节的设计,波纹梁腹板图及单波构形示意图如图1、图2所示。

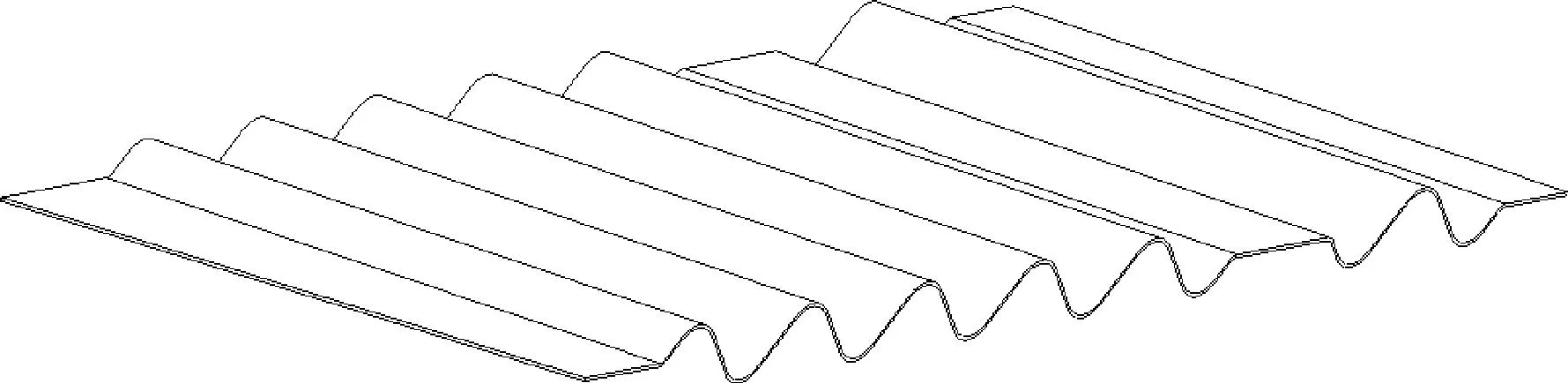
图1 波纹梁腹板图Fig.1 Wave beam web sketch

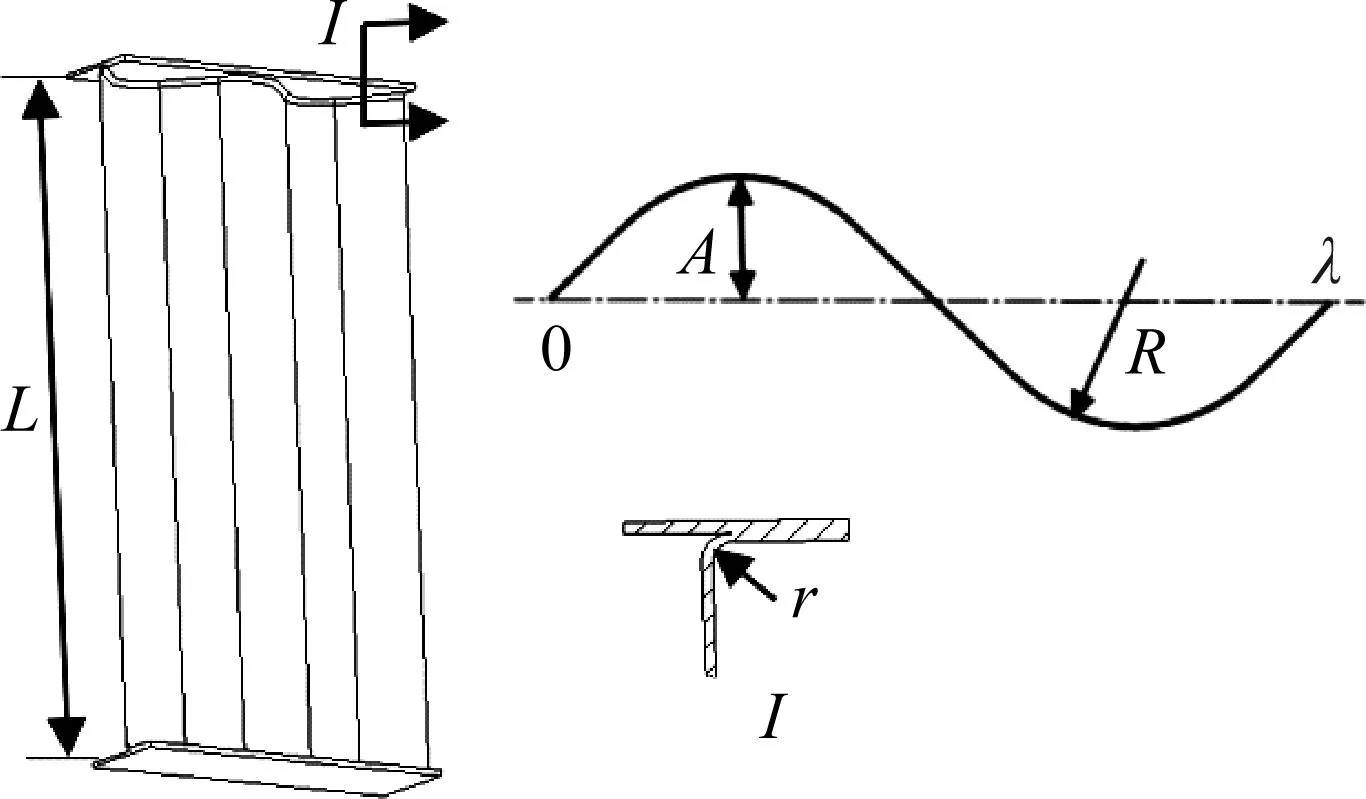
图2 单波波纹梁示意图Fig.2 Single wave beam diagrammatic sketch

参考《飞机设计手册》[16]临界应力与等截面杆长细比的关系曲线,应用短柱范围压溃区可得到下式

(1)

式中:f2(A,ω,δ)为波形面积;Ix为波形惯量矩;L0为波纹梁有效高度;F为压溃截面面积

计算波形惯量矩有

(2)

积分计算波形面积有

(3)

把式(2)、(3)代入式(1)得到

(4)

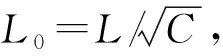
(5)

式中:L为波纹梁实际高度;C为等截面杆端部支持系数;δ为波纹梁厚度,mm。根据不同端部支持条件和加载方式C取值不同,参考《飞机设计手册》第9册工程经验公式,在波纹梁压溃过程中,冲击载荷沿轴向作用于波纹梁杆截面,并在载荷施加于波纹梁端部缘条情况下,波纹梁的波纹腹板约束接近于端部固支,同时波纹梁波纹腹板面为均匀等截面剖面,因此针对本文讨论情况对于杆端部支持系数C取值为4。

式(5)关系式用于判别波纹梁构形进入压溃失稳条件。同时,对于非规则形状截面杆,其必有一个确定的杆剖面最小惯性矩IX值,其定义为各微元面积与各微元至截面上某一指定轴线距离二次方乘积的积分,为保证最小的弯曲惯性矩IX是以波纹梁安装使用的Y平面为对称轴的一个量值,则应满足关系式

(6)

进一步展开,得到

(7)

式中,A和λ分别为波幅、波长。

简化运算后得到A<λ/4,即λ/A>4;特别地,当λ=4A时,波纹梁截面在两个方向的惯性矩是一致的,几何图形上将波长起始点及半波长原点与波幅点相连接,可得到两个正方形(如图3),因此,本文利用关系式λ/A>4控制波纹梁将最小的弯曲惯性矩IX设计在以Y平面为对称。

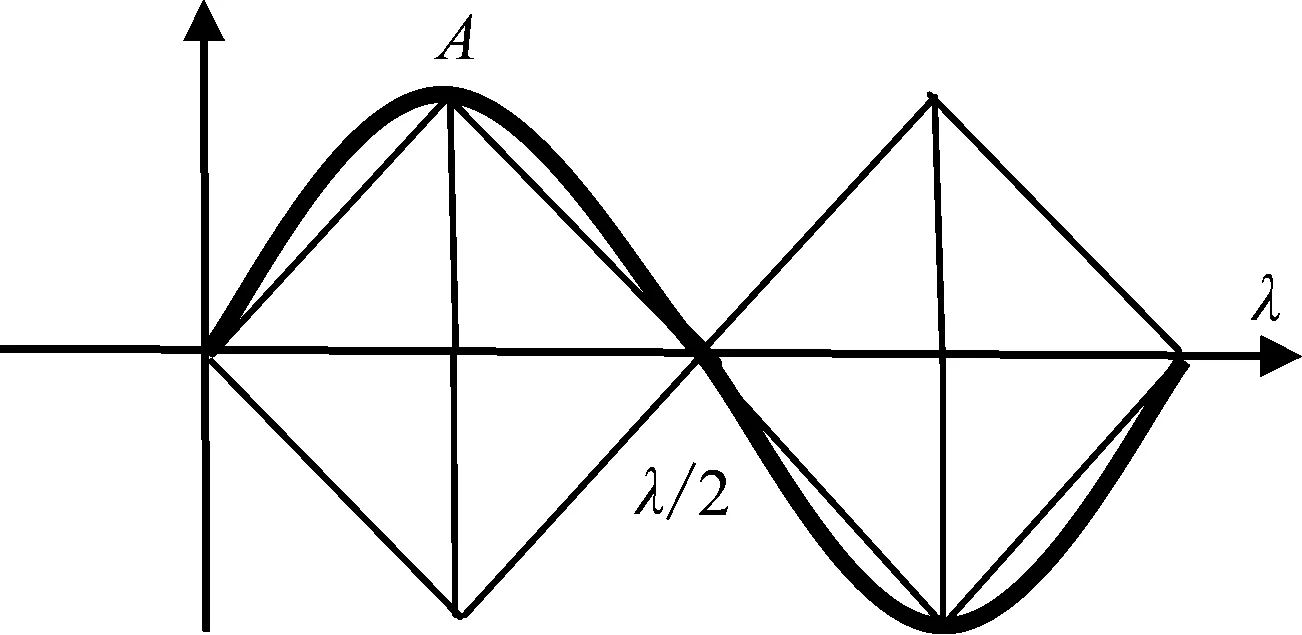
图3 波幅与波长示意Fig.3 Schematic diagram of amplitude and wavelength

当波纹梁设计参数落入不等式(5)同时满足λ/A>4条件时,波纹梁进入压溃失效区,波纹梁材料趋于稳定压损破坏,否则发生失稳后破坏。

波纹梁的波纹腹板圆角形状差异如图4所示。对于不同的波纹腹板圆角R,其差异在于圆弧段受垂向压溃与平直段受垂向压溃表现出的角区应力水平不一样,当圆角接近零,波纹腹板变为三角波构形,这种构形有利于加工和安装设备,但是波形段变成由直线段连接的折线形状,在折线尖角处易产生集中应力载荷,载荷首先传向尖角处角区刚硬区。

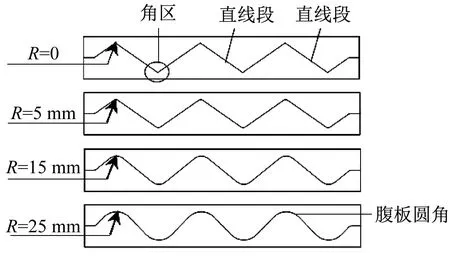
图4 波纹腹板圆角形状差异Fig.4 Difference of circular bead shape on wave-web

同时,因复合材料表现为脆性,需设置合理的破坏触发机制使复合材料结构以可控的形式发生破坏,通常方法为设计薄弱环节,如在波纹腹板端部设计过渡圆角等方式。

综上所述,通过差异化波纹形状及波纹形状参数与梁高关系、设置薄弱圆弧等,设计相应构形波纹梁开展数值模拟及试验研究工作。

2 波纹梁结构吸能特性

评价复合材料波纹梁的吸能特性需考量多方面的因素,从以下几个计算参数评估波纹梁的吸能能力。

比吸能(specific energy absorption,SEA)是衡量复合材料吸能能力的重要指标[17-18];其定义为单位压溃质量的复合材料所吸收的能量,可表达为

(8)

式中:F为载荷;ρ为材料密度;l为长度变量;S为结构截面面积;h为压溃位移。

峰值载荷Fmax为波纹梁破坏时的最大载荷,一般为初始状态时引起结构破坏的载荷。

平均载荷Fav为波纹梁压溃过程中的载荷平均值,计算值为

(9)

3 波纹形梁压溃试验研究

3.1 试 件

选取试验对象分为两组,两组尺寸分别为:

(1) 三波波纹梁:梁高L=400 mm,波长λ=120 mm,波幅A=20 mm, 缘条宽度50 mm,波纹腹板圆角半径R=25 mm,薄弱环节(端部圆角)半径r设置2 mm、4 mm、6 mm三种尺寸。

(2) 三波波纹梁:梁高L=400 mm,波长λ=120 mm,波幅A=20 mm,缘条宽度50 mm,薄弱环节(端部圆角)半径r=3 mm,波纹腹板圆角半径R设置5 mm、15 mm、25 mm三种尺寸。

对于试验件材料体系选择为3234/CF3052/39双向环氧碳布,单层厚度为0.302 mm,腹板铺层顺序为[45°/45°/0°/45°/45°],以及外表面增加一层玻璃布3233/EW110C/44保护碳纤维铺层在运输中不被损伤,总厚度为1.614 mm,每种构形尺寸试验件为6件,总试验件数量为36件。

试件高400 mm,宽360 mm,由上、下缘条及中间波纹腹板组成,铺层材料的主要力学性能如表1所示。

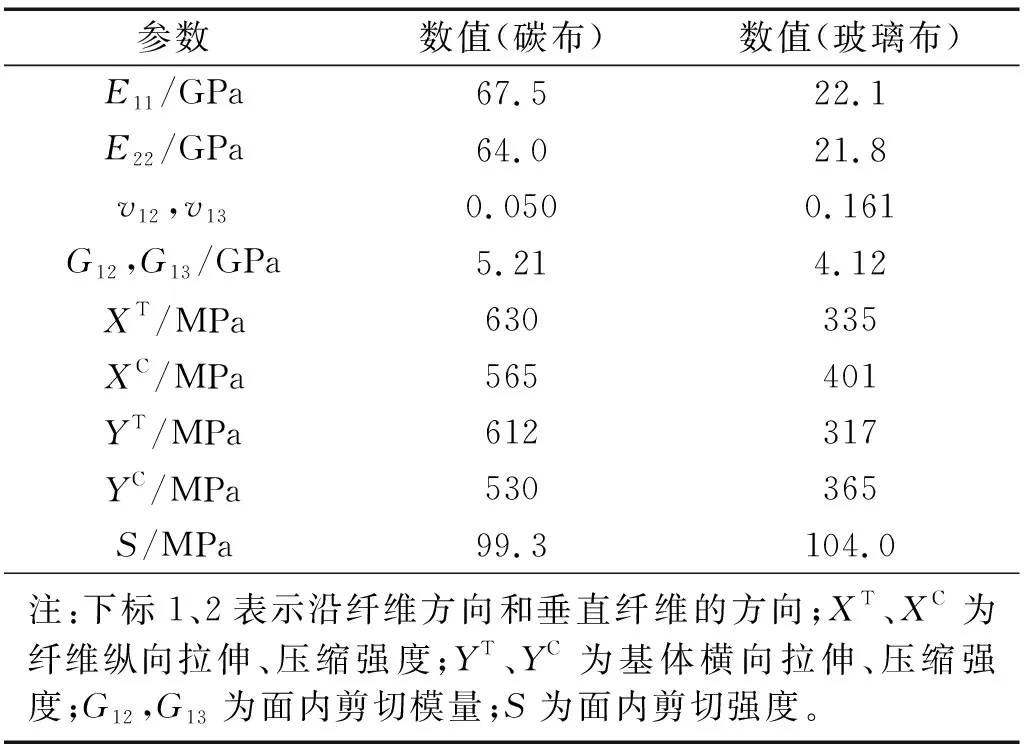
表1 复合材料力学参数表Tab.1 Composite property parameter

3.2 压溃试验

参考GJB 2681—2015《军用直升机抗坠毁要求》直升机垂向撞击速度12.8 m/s,同时考虑机身结构吸能的分配比例,将试验件自由坠落高度设计为4.18 m(触地速度为9.05 m/s),投放质量为70 kg。

试验件的支持方式如图5所示。试验件一端固定在吊篮底部,试验件与坠撞平台相互垂直,试验件的下表面与坠撞平台平行,吊篮上增减配重块数量并固定。坠撞平台下方安装有四个载荷传感器,如图6所示。试验件采用由上下压板组成的专用夹具夹持,上压板装有两个压条,两压条的内侧下部各开一条槽,通过拧紧螺钉将试验件固定在上压板上,同时加装四条限位杆,使得上压板只能在限位杆中上下滑动,防止波纹梁试件在加载过程中扭转。

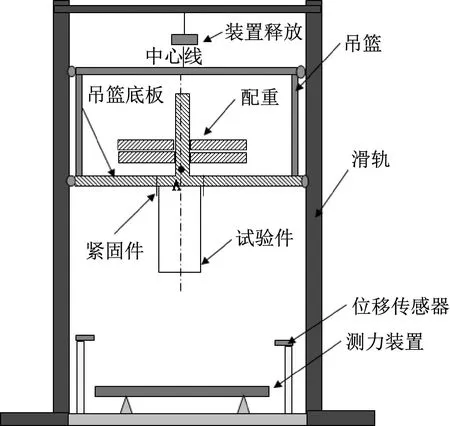
图5 动态压溃试验总体图Fig.5 Dynamic crush experiment conceptual diagram

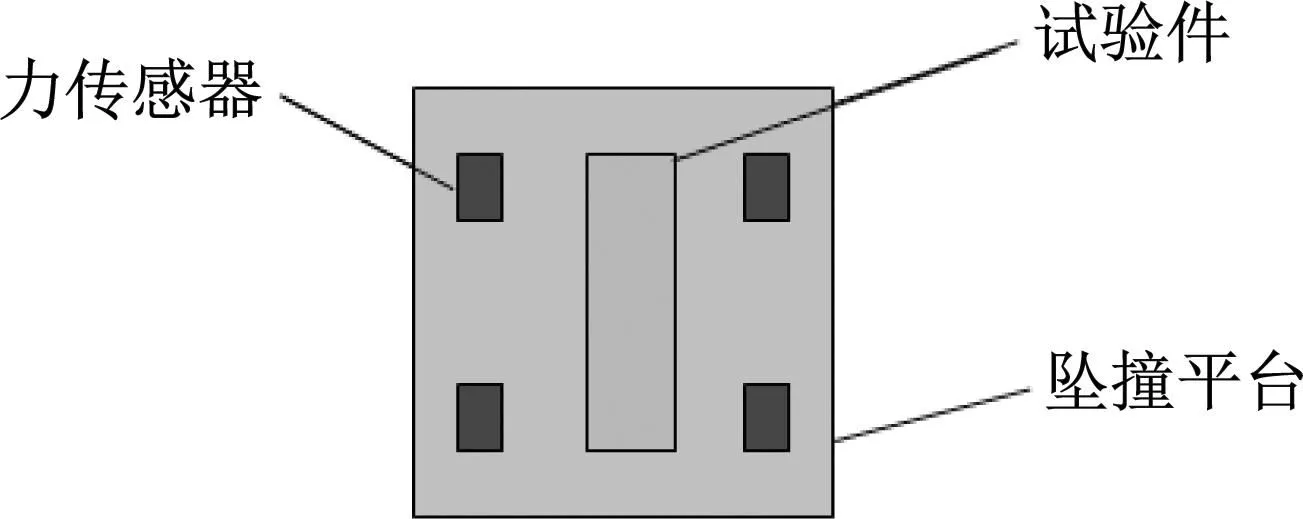
图6 载荷传感器安装示意图Fig.6 Load sensor installation diagram

试验过程中,记录试验件在冲击过程中的载荷-时间历程,通过数据处理得到位移(即试件压缩量)-时间历程;拍照记录各试验件的破坏情况。

试验在室温环境下进行(约为20 ℃),相对湿度约为76%。

3.3 试验结果

从试验情况来看,在坠撞冲击过程中,不同尺寸构形波纹梁的损伤破坏情况存在差异;第一组r=2 mm、r=4 mm尺寸波纹梁压溃较为稳定,试验件大部分从端部圆角一端开始破坏,粉末状及片状碎片飞溅而出,发生稳定渐进压溃伴有碳纤维粉末状物;r=6 mm有1件自由边局部失稳开裂,另有1件试验件变形的后阶段波纹腹板出现向里向外偏折,发生局部失稳与稳定压溃混合破坏;同时,该构形其他几个试件呈现稳定的压溃过程说明这种局部失稳现象的出现与试件破坏模式密切相关的。

对于压溃位移及载荷情况,r=2 mm尺寸试验件压溃位移量整体高于r=4 mm、r=6 mm试验件;峰值载荷r=2 mm、r=4 mm尺寸构形试验件整体高于r=6 mm试验件,平均载荷r=6 mm试验件整体最高,r=2 mm试验件次之,r=4 mm试验件最小;平均载荷决定了波纹梁的总体吸能能力,平均载荷低对吸能要求不利;第一组所有试件的压溃位移量及峰值/平均载荷如图7所示。

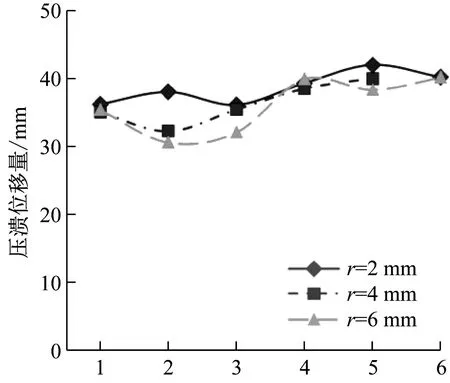
(a) 第一组试验件压溃位移量

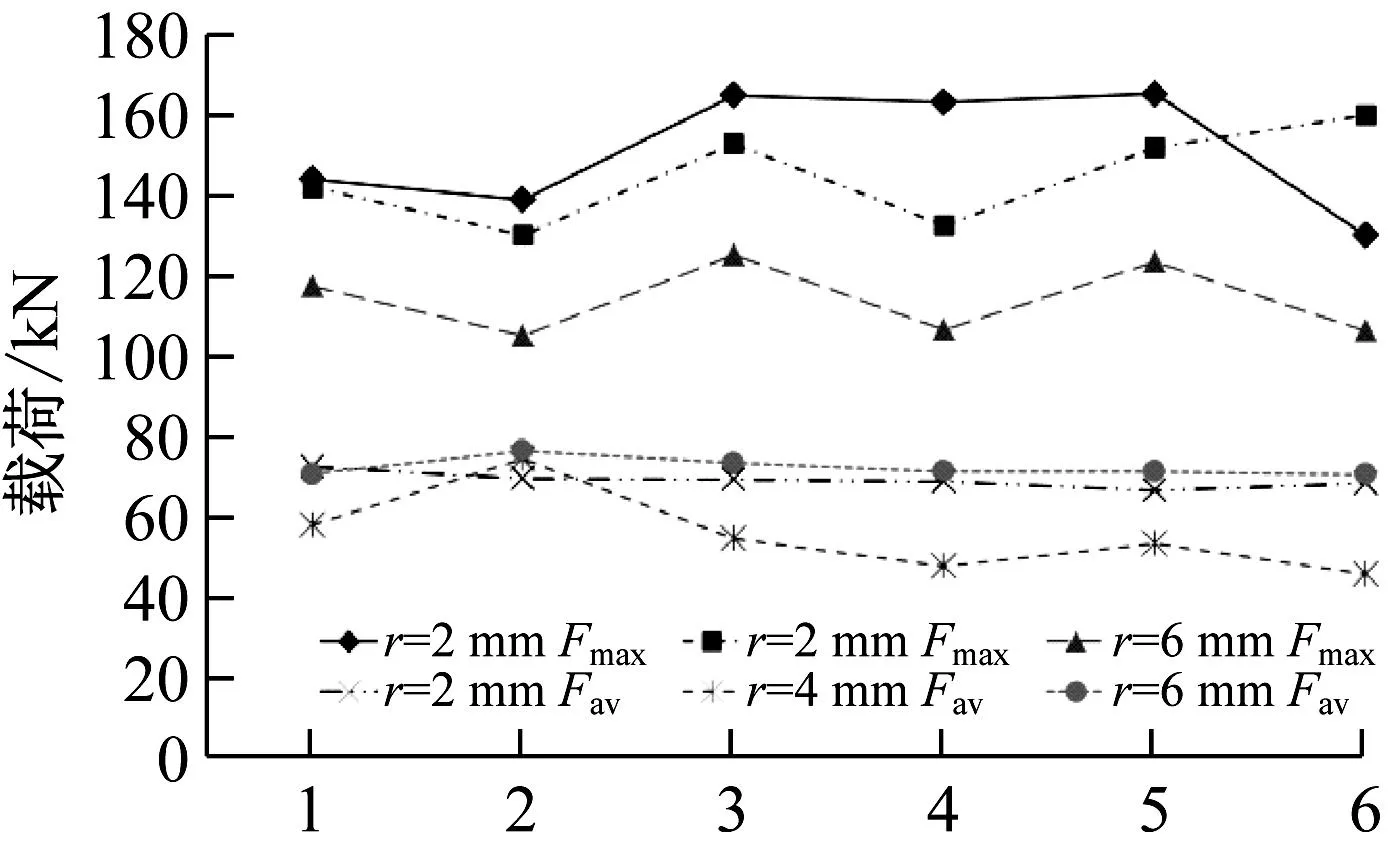
(b) 第一组试验件峰值/平均载荷图图7 第一组试验件压溃位移量及峰值/平均载荷Fig.7 The first group load-displacement curve and maximum/ aveage load

第二组试验件中R=5 mm构形有1件底部失稳断裂压溃时自由边发生扭转偏折;R=15 mm、R=25 mm各有1件发生局部失稳与稳定压溃混合破坏现象,失稳部位位于上端部边缘,出现不规则折断破坏现象;其余试验件较为稳定渐进压溃破坏,粉末状及片状碎片飞溅而出,伴有碳纤维粉末状物。

R=5 mm尺寸试验件压溃位移量整体高于R=15 mm、R=25 mm试验件;

峰值载荷及平均载荷R=5 mm、R=15 mm、R=25 mm及试验件整体上依次增高。第二组试验件压溃位移量及峰值/平均载荷如图8所示。

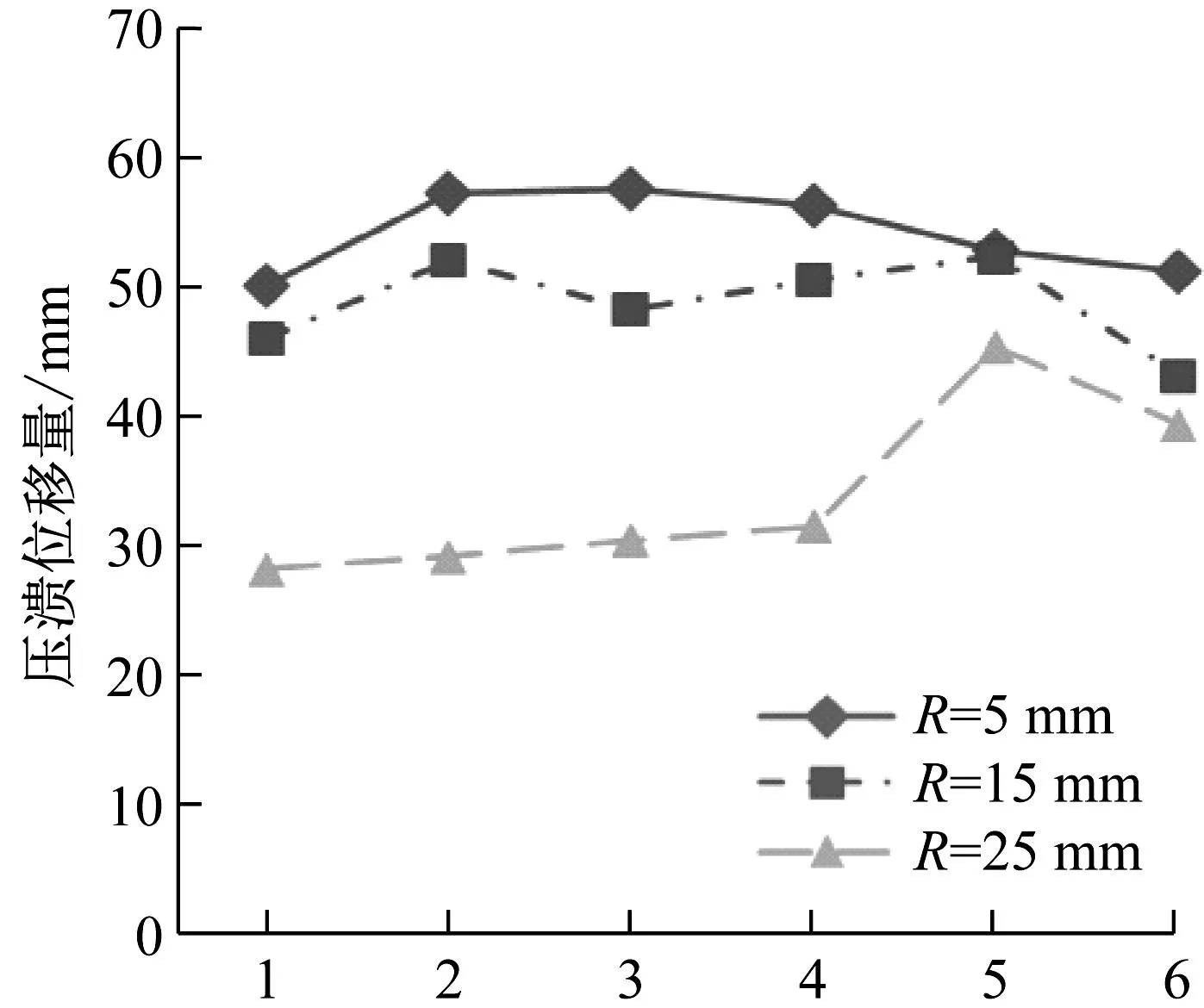
(a) 第二组试验件压溃位移量

对于有些试验件波动较大的试验数据结果予以剔除(包括失稳破坏数据),取平均值为获得的试验结果,处理得到试验结果如表2所示。

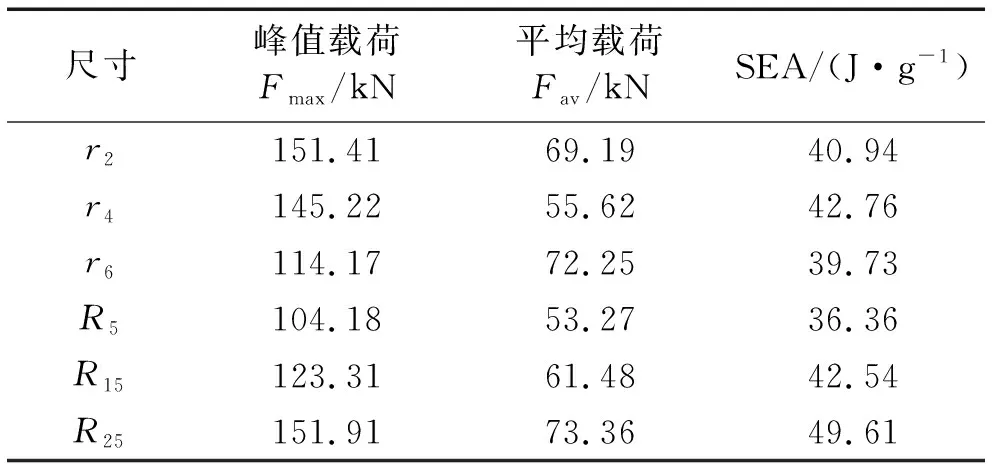
表2 试验结果平均值Tab.2 Average value of test results

图9 波纹梁压溃试验Fig.9 Wave beam crash test

4 数值模拟理论

4.1 失效准则与刚度退化

复合材料波纹梁在冲击载荷作用下的失效机制非常复杂,在数值计算中,考虑刚度退化,利用基于Hashin准则编写材料子程序Vumat模拟复合材料的失效模型。

Hashin失效准则共分为纤维拉伸、纤维压缩、基体拉伸和基体压缩四种失效模式,对应以下四个公式用于判断材料点的起始损伤

(10)

(11)

(12)

(13)

式中:XT,XC为纤维纵向拉伸、压缩强度;YT,YC分别为基体横向拉伸、压缩强度;SL,ST分别为面内剪切强度和层间剪切强度;σ为铺层应力,下标1、2表示沿纤维方向和垂直纤维的方向。

引入参数K[19]=ST/SL将ST转化为平面状态剪切强度SL,并将修正材料参数K代入式(13),得到:

(14)

损伤演化基于Matzenmiller[20]模型进行刚度退化,材料刚度退化程度的损伤状态变化量定义为d,材料本构关系表示为

σ=C(d)ε

(15)

其中,

(16)

D=1-(1-df)(1-dm)v12v21>0

(17)

式中:df为纤维方向损伤状态变量;dm为基体方向损伤状态变量;ds为剪切损伤状态变量;E1、E2、G为材料初始模量;v12、v21为材料初始泊松比。

df、dm和ds可表达为

(18)

(19)

(20)

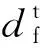
损伤变量d统一表达为

(21)

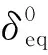
损伤演化的本构三角形如图10所示[21]

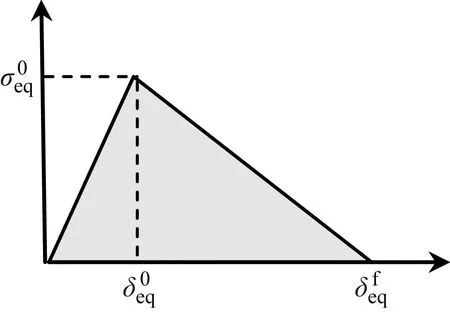
图10 损伤演化的本构三角形Fig.10 Constitutive triangle of damage evolution

纤维拉伸、纤维压缩、基体拉伸、基体压缩状态下四种等效位移及等效应力的表达式为

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

式中,LC为单元特征长度。根据式(10)～(13)以及式(22)～(29),可得到每个材料点随着载荷增加,在对应失效模式下的损伤起始位移和等效强度。

而材料单元彻底失效时对应的失效位移由式(30)计算得到

(30)

式中,GC为临界应变能释放率,即图11所示三角图形面积。代入独立损伤状态变量d求解计算得到,

纤维拉伸:

(31)

(32)

纤维压缩:

(33)

(34)

基体拉伸:

(35)

(36)

基体压缩:

(37)

(38)

4.2 有限元模型的建立

设计两组波纹梁模型研究构形参数对波纹梁吸能能力的影响。

第一组模型波纹腹板圆角R值及薄弱环节r值设置为常量25 mm及2 mm,梁高L、波幅A及波长λ设计为变量。在保持波长λ不变的情况下,通过控制梁高L及波幅A值关系式比值探讨工程算式(5)对于波纹梁坠撞吸能能力影响的适应性,尺寸如表3所示。

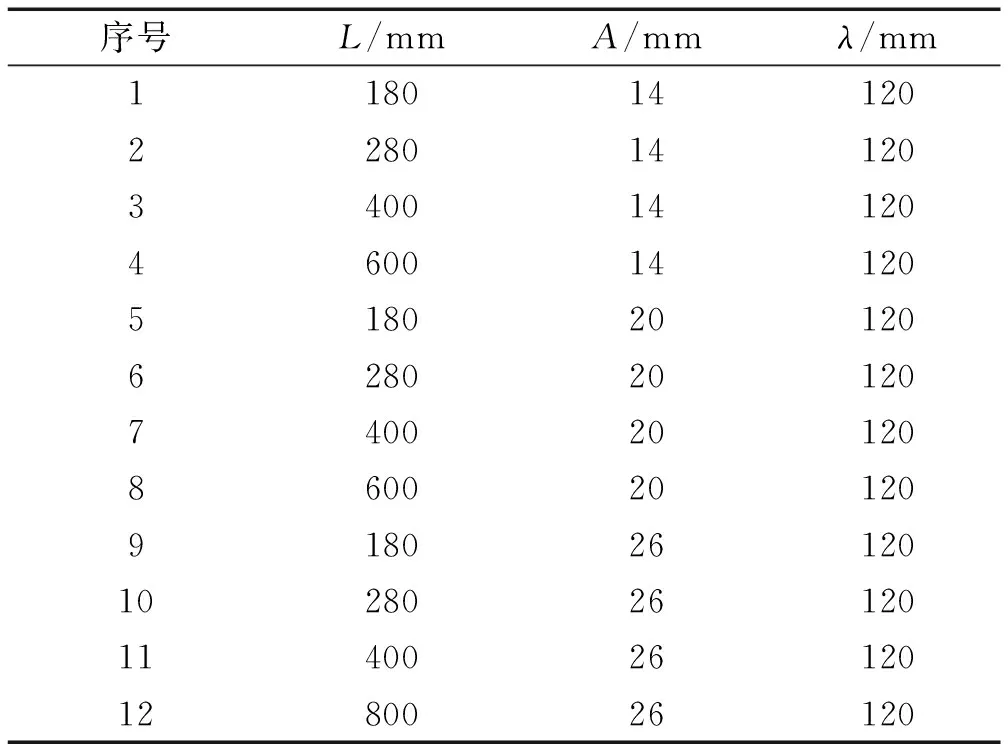
表3 第一组模型参数尺寸表Tab.3 The first group of model parameter size

第二组模型,梁高L、波幅A及波长λ设置为常量分别为400 mm、20 mm以及120 mm,波纹腹板圆角R及薄弱圆角r设计为可变变量,研究波纹腹板圆角及薄弱圆角对坠撞吸能能力的影响,尺寸如表4所示。

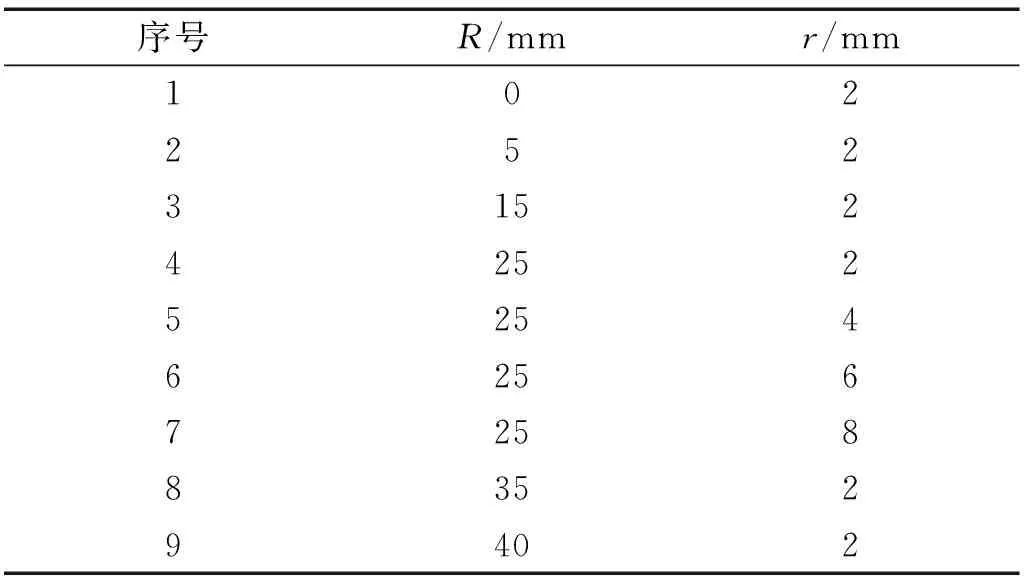
表4 第二组模型参数尺寸表Tab.4 The second group of model parameter size

波纹梁轴向压溃的有限元模型底面设置为刚性平面,由于波纹梁的铺层厚度小于其有效长度尺寸的0.5%,因此模型整体结构(包括刚性平面)可采用壳单元模拟。模型中使用了四节点缩减积分壳单元S4R,单元属性设置为各向异性,共建立6 956个壳单元,腹板近似全局尺寸为5,刚性平面近似全局尺寸为10。

在对波纹梁模型的波纹腹板划分网格时,为提高网格划分质量使计算结果更准确,吸能部件一个波长最少需要划分6个单元,以10～12个单元为最佳,如图11所示。

图11 吸能部件波长示意图Fig.11 Wavelength sketch of absorb energy component

对于薄弱环节倒圆角的网格划分,采用细小单元模拟实际的小圆弧薄弱环节,根据圆角半径大小采用以下原则近似建模,当半径小于2 mm,可忽略圆角;当半径2～4 mm,用一列单元模拟,当半径4～6 mm,用两列单元模拟;当半径大于6 mm,至少三列单元模拟,如图12所示。

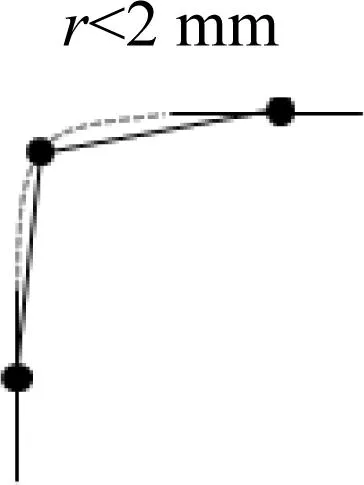
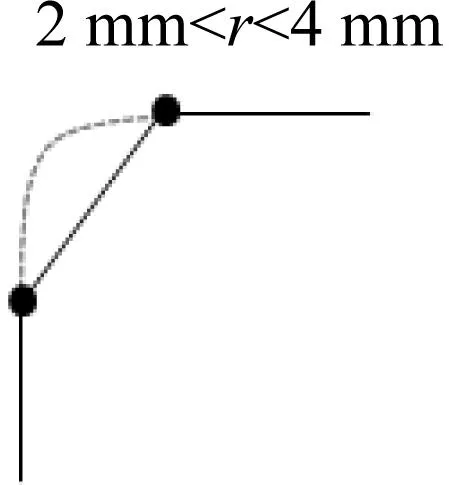
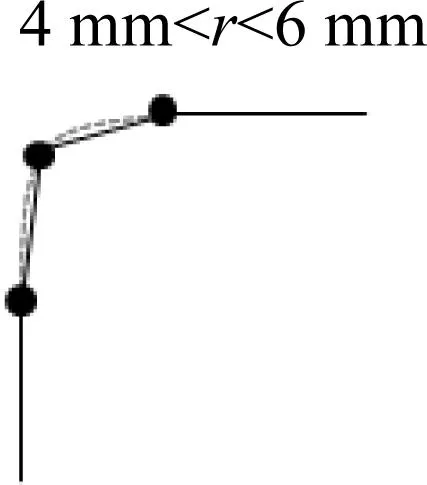
图12 小圆弧圆角划分示意图Fig.12 Partition sketch of small arc circular bead

有限元模型材料为5224/CF3052/39高温固化环氧碳布预浸料,腹板铺层顺序为45°/45°/0°/45°/45°,外表面铺一层5224/EW110C/44玻璃布,总厚度为1.6 mm,模型材料的力学参数见表1。

在上缘条与波纹腹板之间作tie约束,保证相对位置关系不变,一起以初始速度9.05 m/s撞击下刚性平台,方向沿Z轴负向。根据研究内容为得到计算峰值载荷、平均载荷和吸能能力等参数,可将上缘条约束简化为施加位移自由度外,其他自由度固定,建立有限元模型如图13所示。

图13 有限元模型示意图Fig.13 Finite element model sketch

4.3 仿真及结果分析

提交计算,积分步长为0.001,积分时长为0.04。计算历时120 min,部分波纹梁模型数值模拟云图如图14所示。

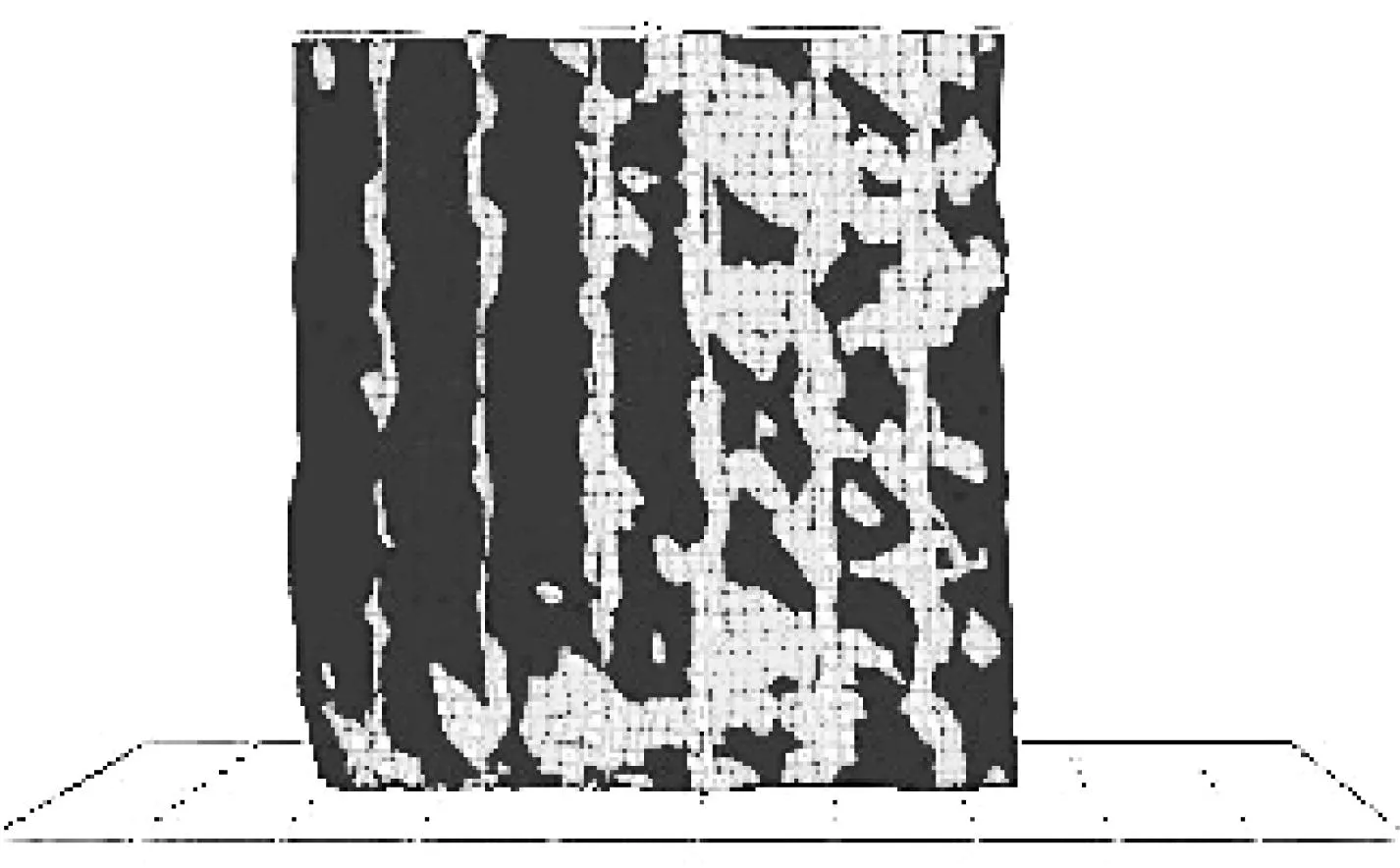
图14 部分波纹梁模型云图Fig.14 A part of wave beam model cloud

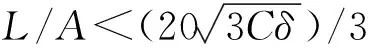
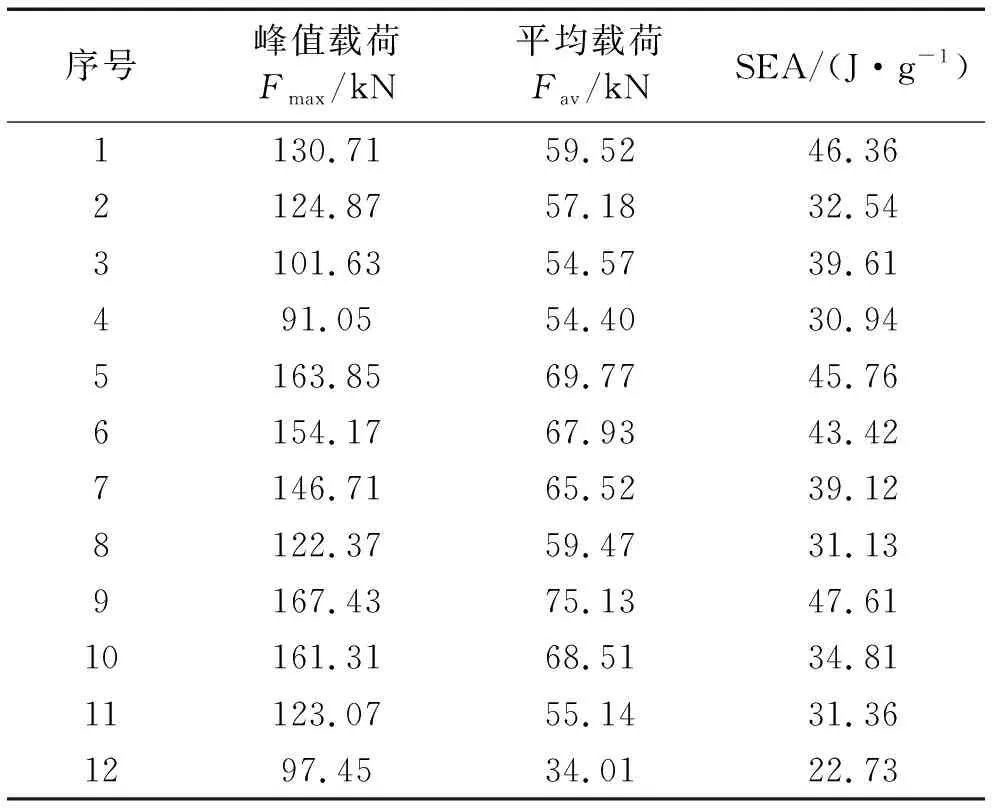
表5 第一组波纹梁计算结果Tab.5 The first group of wave beam simulation result

对于第二组模型,序号1、2波纹梁相对于同组其他模型,上下边缘初始应力较小,载荷往中间段波纹腹板集中,根据压溃时的变形云图可以发现,R值较小(R=0、5 mm),压溃初始应力主要集中在角区尖角边(三角波)处,该处产生角区刚硬区,发生局部不稳定现象,对波纹梁压溃失效产生了不同的影响,由于较刚硬的角区继续承受增加的压缩载荷,载荷增加到一定的量值时发生断裂破坏,然后随着压溃过程的继续,应力传递到结构元件其他位置;序号4-7波纹梁模型载荷也往中间段波峰、波谷处集中,但分布范围比1、2大很多,较为均匀,序号8、9波纹梁模型载荷自始至终较为均匀地分布在整个腹板面内,这说明R值大(R=25 mm、35 mm、40 mm)时,初始压溃应力较为均匀,压溃过程应力加载和传递也较均匀。如表6所示。

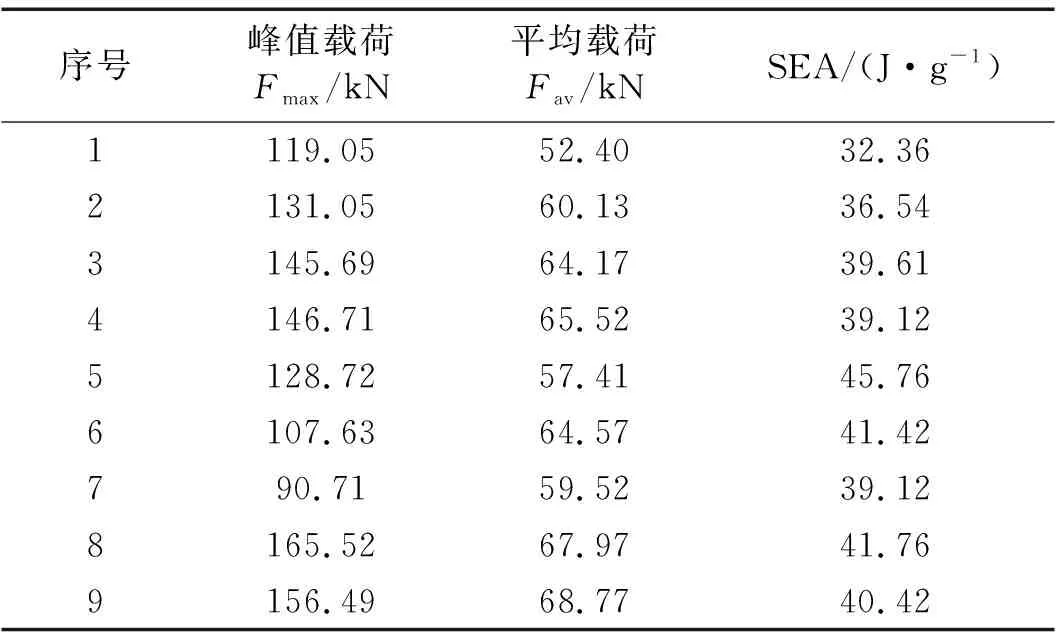
表6 第二组波纹梁计算结果Tab.6 The second group of wave beam simulation result

数值模拟计算得到不同构形波纹梁的吸能数据如表5、表6所示,对载荷-位移曲线进行数值积分,得到压溃过程通过波纹梁损伤破坏所吸收的能量,载荷-时间曲线及吸收能量值如图15、图16所示。

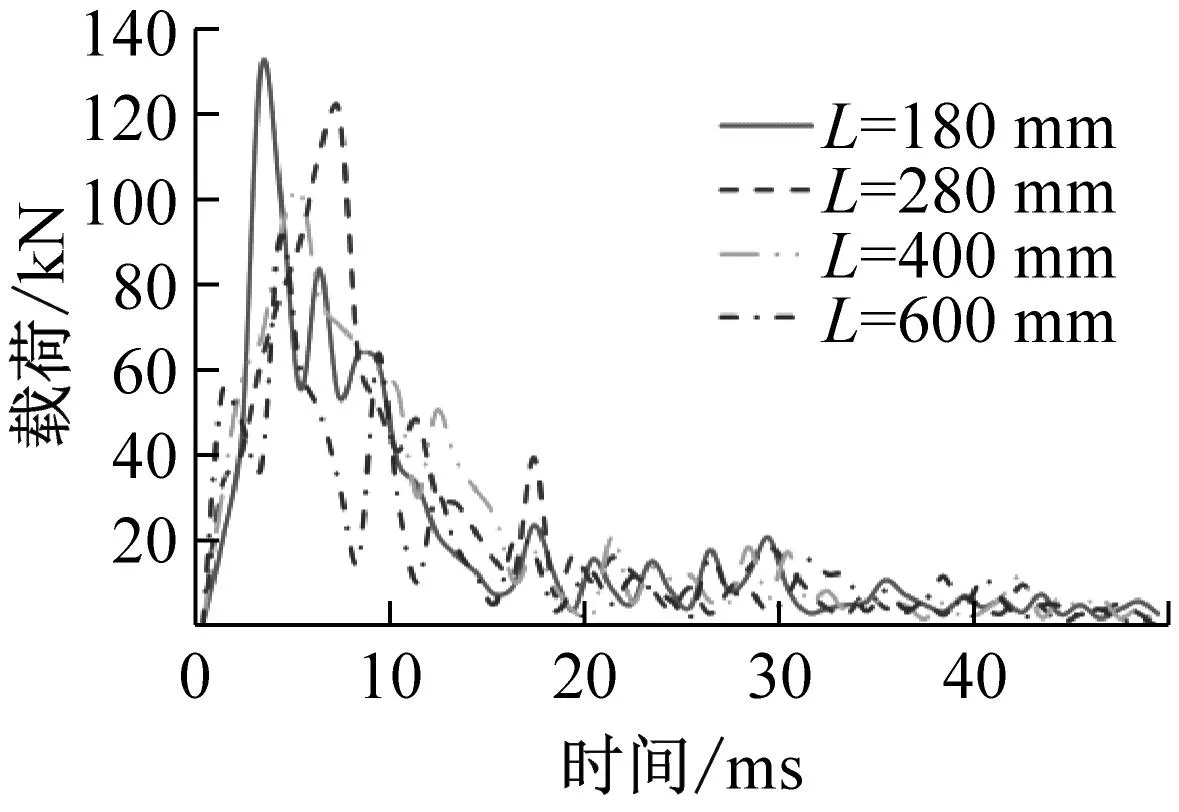
(a) 波幅A=14 mm

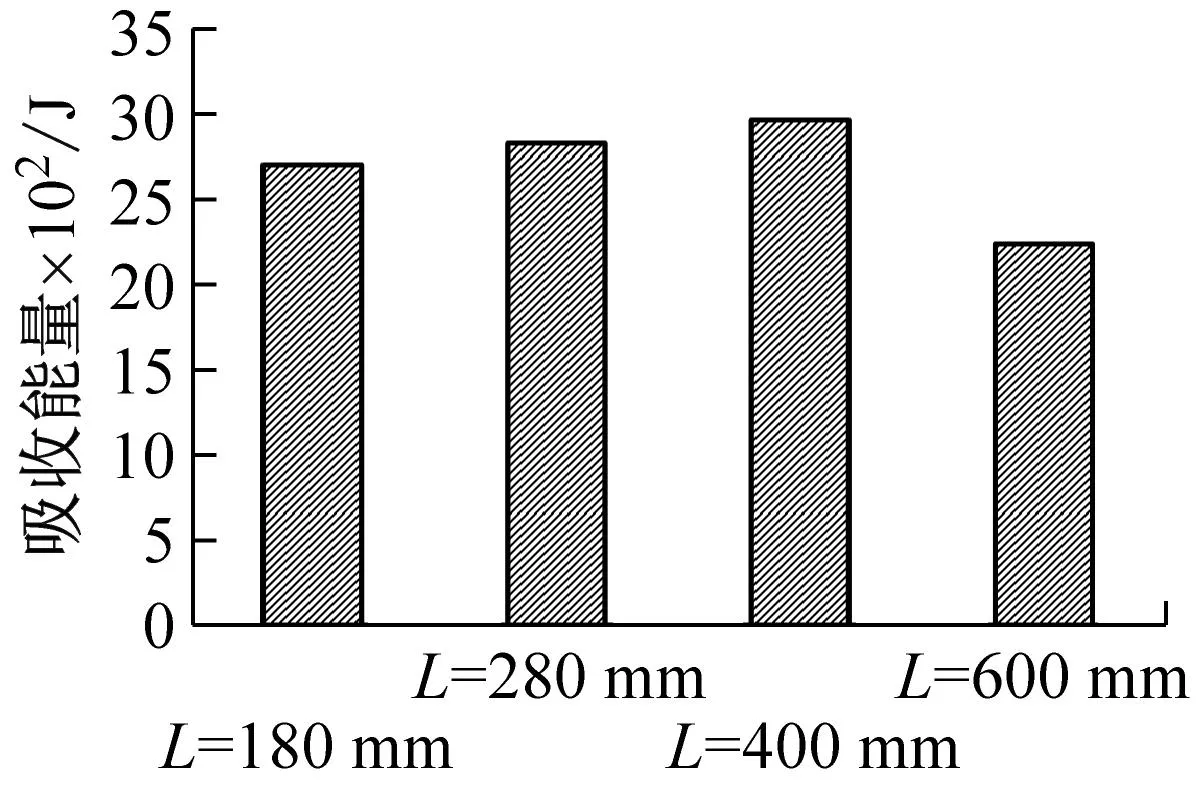
(b) 波幅A=14 mm

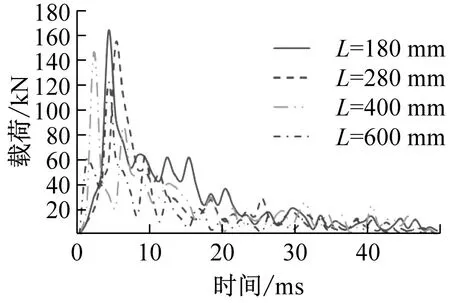
(c) 波幅A=20 mm

(d) 波幅A=20 mm

(e) 波幅A=26 mm

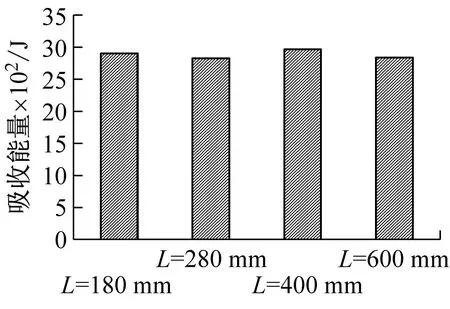
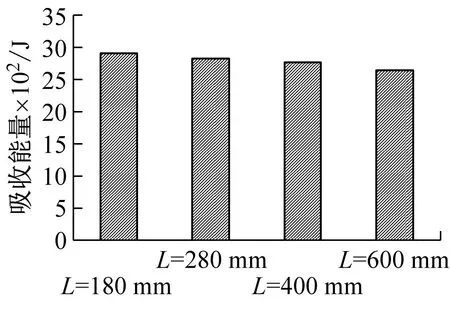
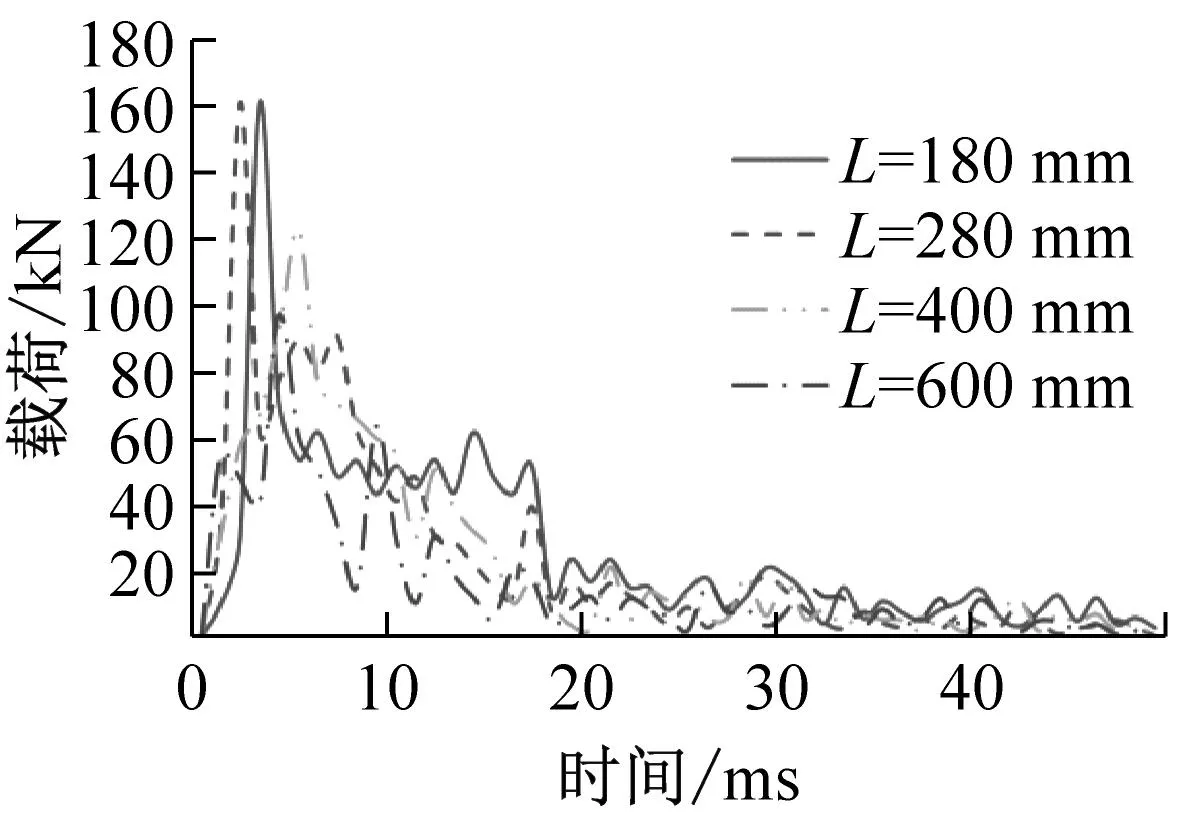
(f) 波幅A=26 mm图15 第一组载荷-时间曲线及吸收能量值Fig.15 The first group load-time curve and absorbed energy value

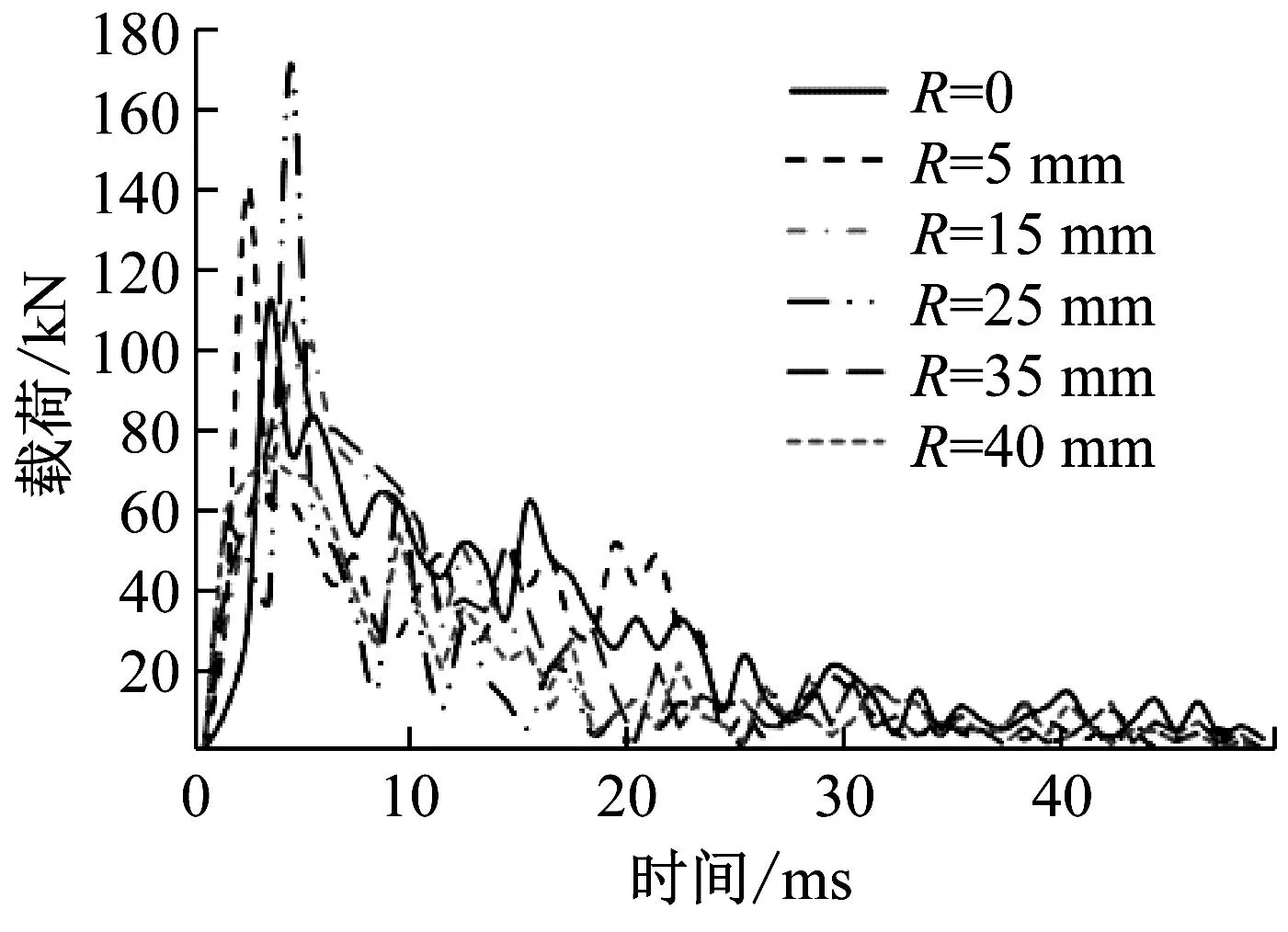
(a) 薄弱环节r=2 mm

(b) 薄弱环节r=2 mm

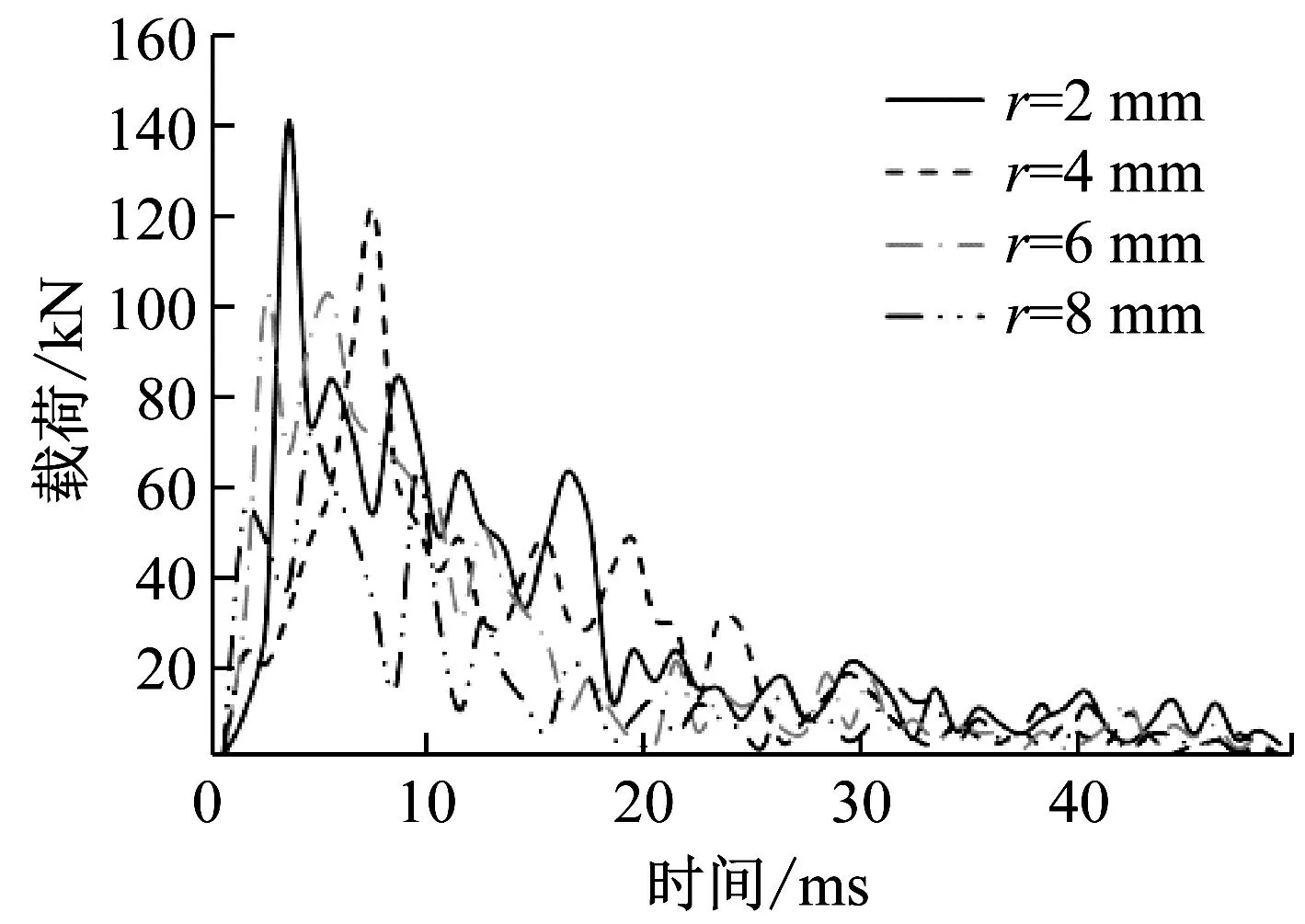
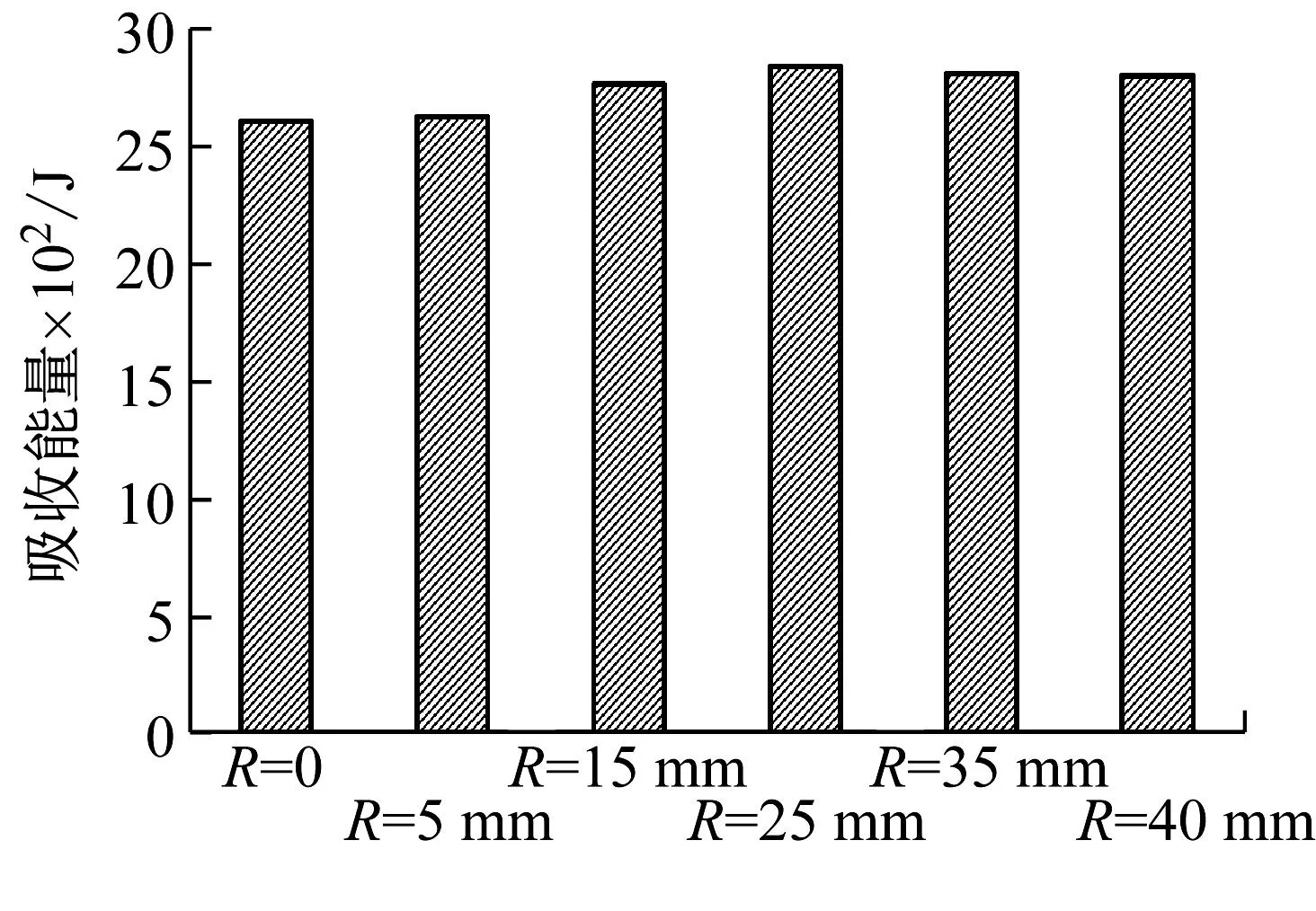
(c) 波纹腹板圆角R=25 mm

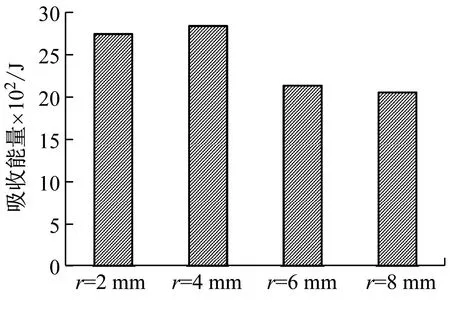
(d) 波纹腹板圆角R=25 mm图16 第二组载荷-时间曲线及吸收能量值Fig.16 The second group load-time curve and absorbed energy value

对于第一组模型,在满足稳定压溃情况下,对于相同波幅A时,随着高度值L增加(L/A值增大)波纹梁的峰值载荷存在差异,变化范围在5%～45%范围内;材料比吸能率序号1、5、6、9、10及11波纹梁较高,对于序号1模型虽然比吸能率高,但峰值载荷也过高,且受限尺寸大小,压损吸能段小,总吸收功量要比序号2及3模型低。

从第二组数据及压溃载荷曲线图中可以看出,随着R值的增大,波纹梁压溃过程中峰值载荷呈增加趋势,R为0和5 mm时峰载相差了10%左右,但R为25～40 mm时峰值载荷差值不大,吸收功量略有差异;波纹有圆角过渡(R>0)波形比三角波(R=0)有利于承载时使波纹梁应力分散传载,防止结构角区尖边或某部位应力过高发生崩溃性破坏。

从表6中可以看出,不同薄弱环节圆角r值对其碰撞过程中产生的峰值载荷水平影响不同,当薄弱环节r较小时,波纹梁峰值载荷会明显增加,随着薄弱环节圆角值r的增大,峰值载荷大体呈减小趋势。在分析计算的几种薄弱环节r角值中,r=2～4 mm诱角值对于降低值峰值载荷及提高平均载荷较为理想,而平均载荷的较高,有利于提升能量吸收值大小。

5 试验结果与数值分析对比

通过对复合材料波纹梁吸能压溃试验研究,探讨了波纹梁损毁形式,获得其承载能力和吸能能力等数据。将第一组试验数据与数值模拟的第二组模型4、5和6计算结果作对比,得到数值模拟与试验结果载荷-位移及吸收能量对比如图17所示。

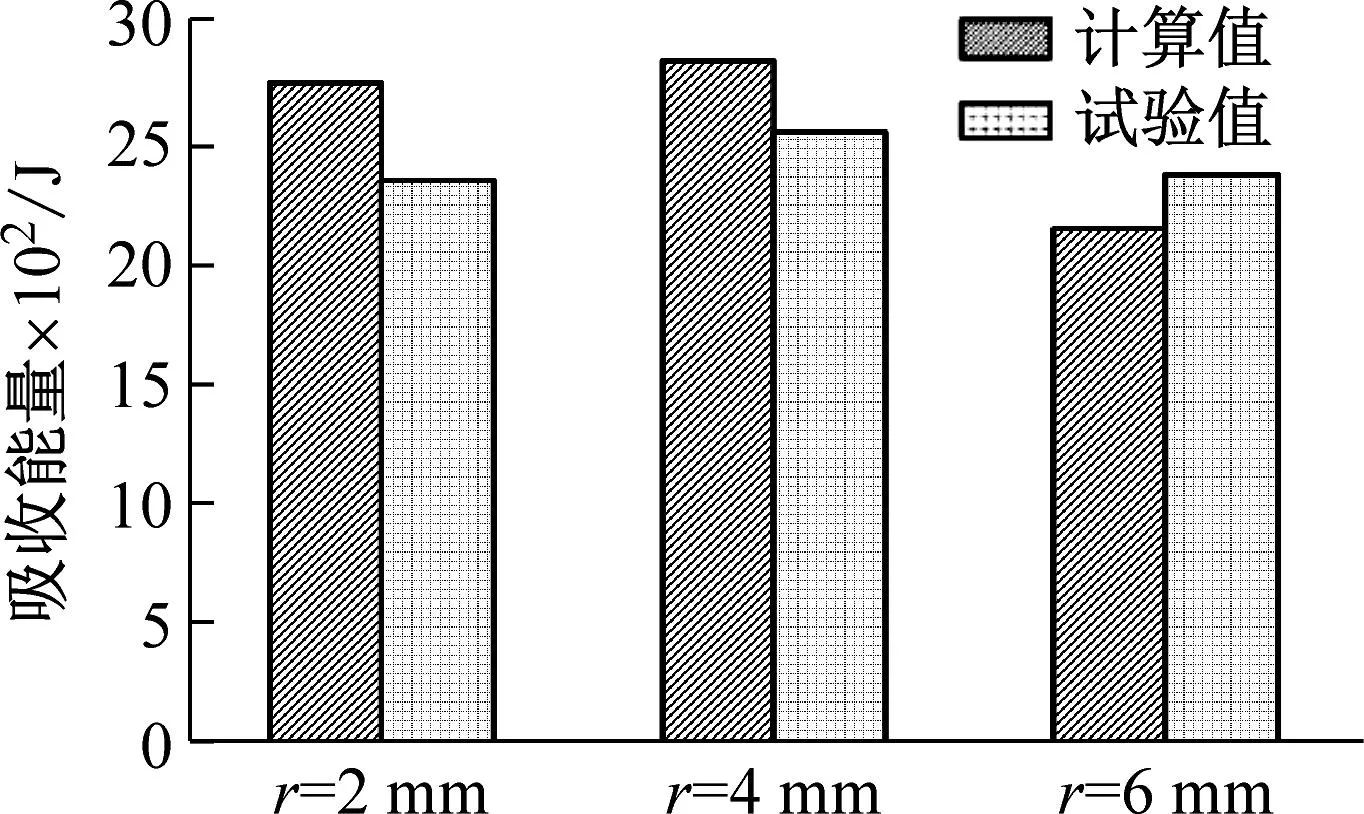
(a) 能量吸收对比

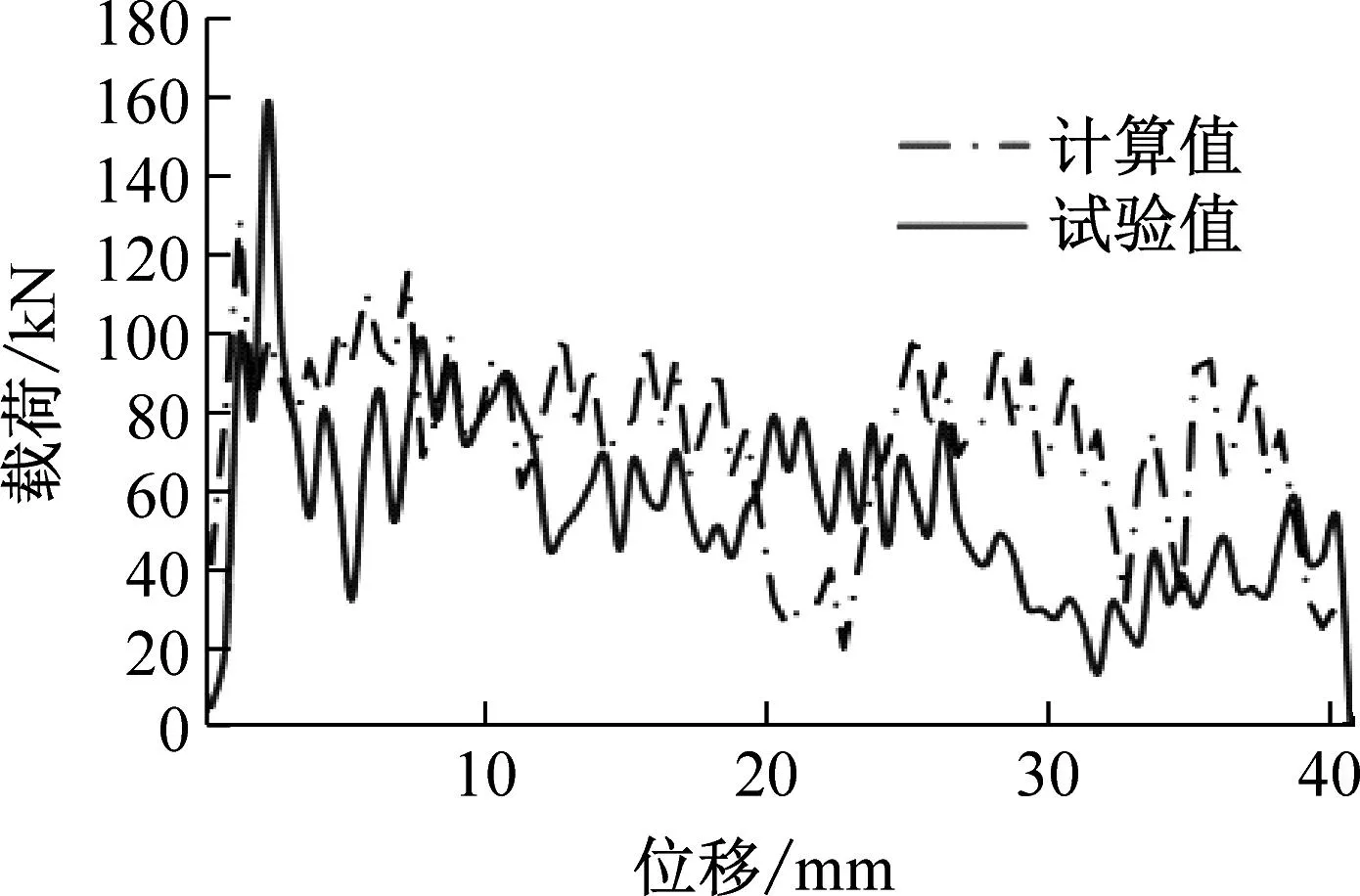
(b) r=2 mm载荷-位移对比

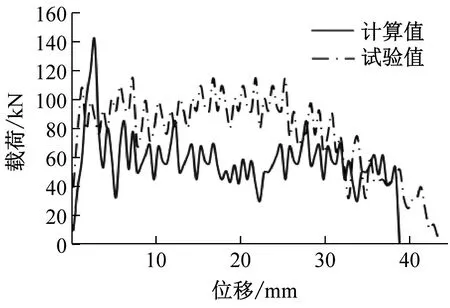
(c) r=4 mm载荷-位移对比

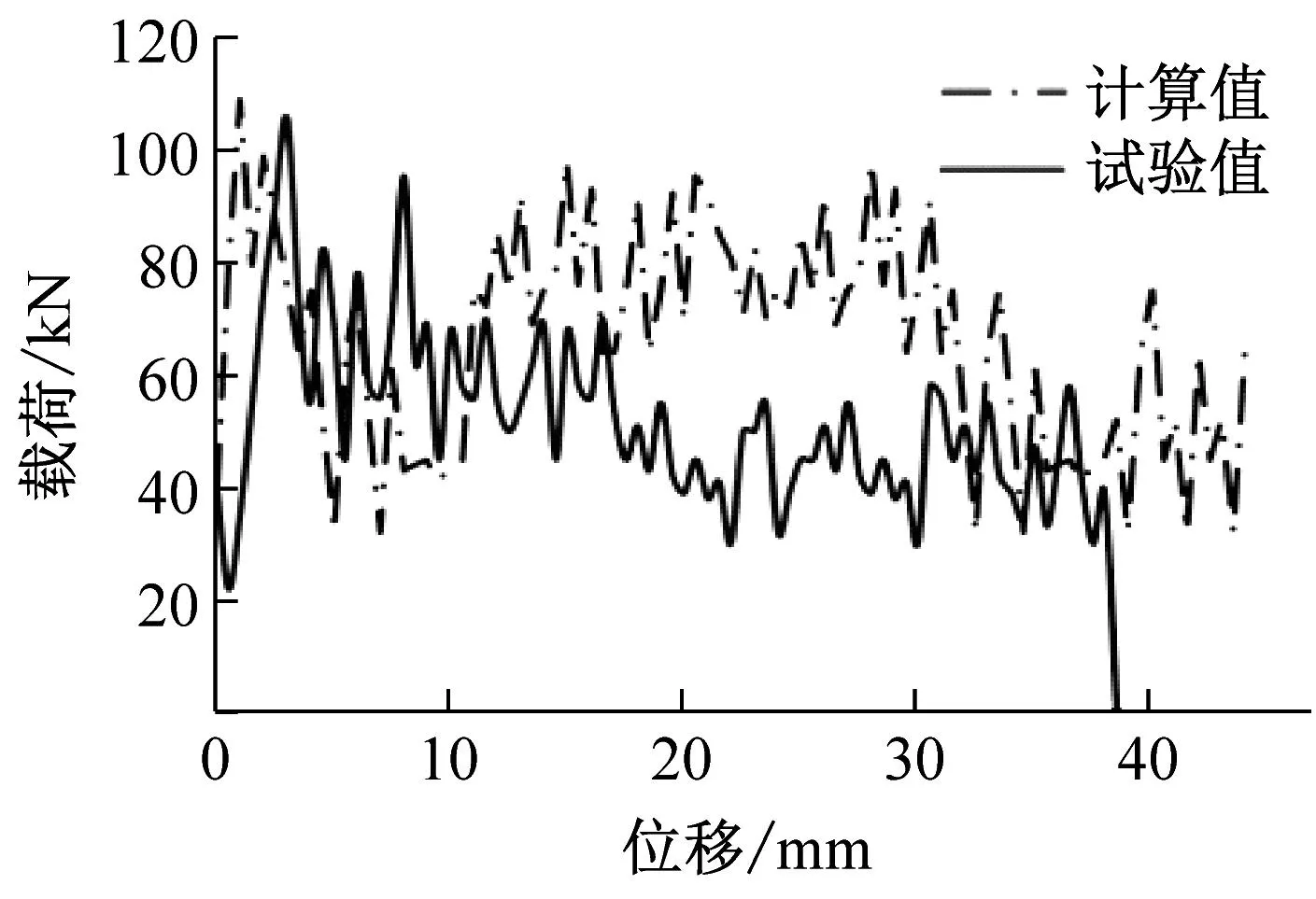
(d) r=6 mm载荷-位移对比图17 数值模拟与试验曲线对比Fig.17 The simulate compare with experiment

通过数值模拟过程与试验压溃过程比较,可以发现,波纹梁的破坏过程宏观上较为相似,大部分都是从薄弱环节处首先压溃,然后从此处开始向上渐进破坏。对载荷-位移曲线与吸能参数的数值比较,试验得到的曲线形状、峰值载荷、平均载荷以及比吸能能力等数值与数值模拟结果相对误差小于14%。

这说明运用ABAQUS有限元软件基于Hashin失效准则,并利用编写VUMAT材料子程序实现层合板单元损伤判定和刚度折减,来模拟复合材料破坏过程和吸能能力是可行的。试验结果与数值模拟结果对比如表7所示。

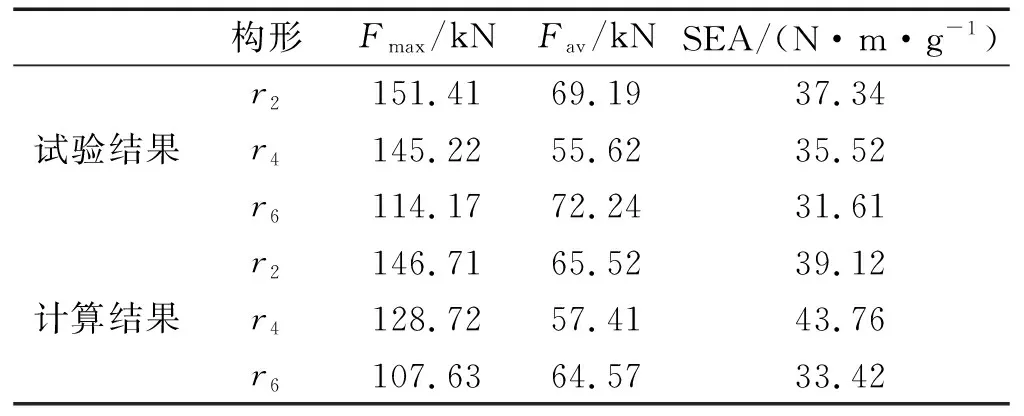
表7 试验结果与数值模拟结果对比Tab.7 Experiment results compare with simulate

数值模拟方法没有考虑复合材料分层破坏,使得模拟得到的平均载荷值整体较试验值略低。

6 结 论

(1) 采用有限元软件ABAQUS模拟波纹梁结构的坠撞过程,并利用编写的Vumat材料子程序基于Hashin失效准则对层合板单元进行损伤判定和失效单元刚度折减;对比分析波纹梁结构元件压溃试验结果误差范围在14%内,验证了数值模型及分析方法的有效性,具有一定的工程使用价值;

(3) 通过对典型复合材料波纹梁结构元件进行试验研究及数值模拟,探讨了设计参数波纹腹板圆角R值对波纹梁压溃时的峰值载荷、平均载荷的影响,根据试验及数值模拟结果分析波纹梁腹板圆角过渡(R>0)波形对比三角波(R=0)有利于角区应力扩散;随着波纹腹板圆角R值增大,波纹梁峰值载荷、平均载荷相应增加,同时圆角值增大意味着波纹梁腹板面积增大,会增加结构材料使用重量,从数值模拟结果来看,在R过大时比吸能率反而有所减少,吸收功量并没有增高,所以需要合理的选择R值设计值大小;

(4) 最后研究了薄弱环节圆角r值大小对波纹梁压溃过程的影响,稳定持续的压溃破坏是吸能的主要阶段,薄弱环节圆角r值增大可显著降低峰值载荷,对平均载荷和吸能的影响由材料性能、试件的稳定性综合决定。