关于幂的图形证明

文／万广磊

超市里有些水果摆放成金字塔的形状，从上往下数，第一层有1个，第二层有4个，第三层有9个，以此类推，如果是第n层，就有n2个苹果（n≥1）。那么，把每一层的水果都加起来，一共有多少个苹果呢？也就是计算12+22+32+…+n2，结果等于多少呢？

随着学习的深入，我们会接触到一个公式，即12+22+32+…+n2=n≥1。怎么来证明这个公式的正确性呢？下面，我们通过图形来探究一番。

方法一

我们先来验证12+22+32+42的结果。如图1，我们用小正方体的个数来分别表示12、22、32、42，下方红色的立体图形是由对应的上方白色的立体图形拼接而来。

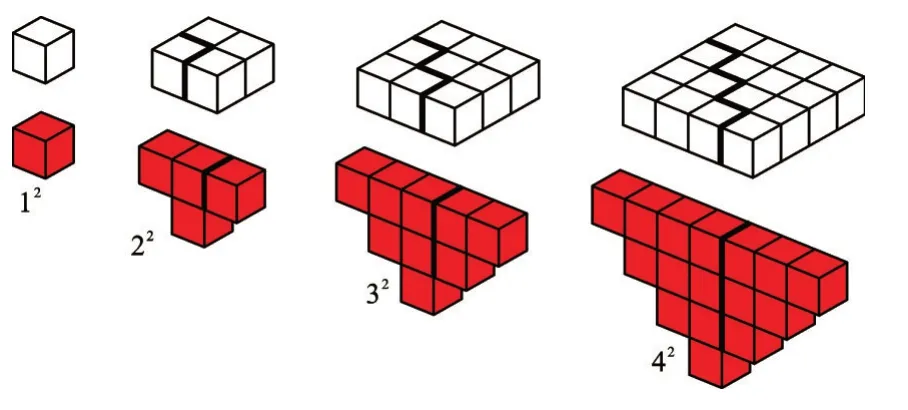
图1

图2—图4 中，小正方体的总量都可以表示12+22+32+42。

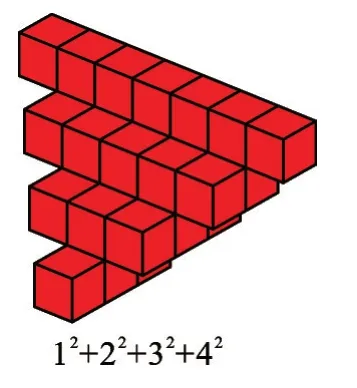
图3

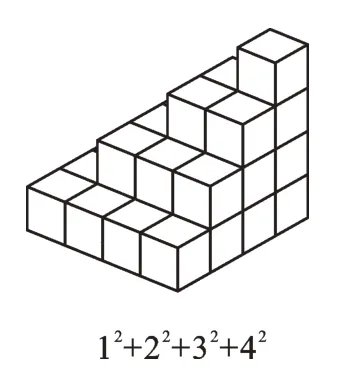
图4

我们将图2—图4 拼接在一起，得到图5，加粗的黑色线条是拼接线。

图5

将两个图5 中的图形再拼接，便得到图6。

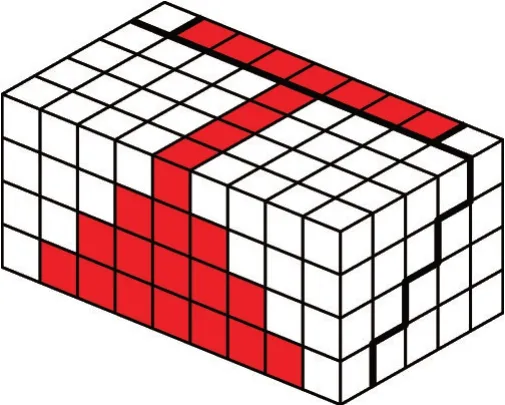
图6

图6 是一个长方体，其体积可以表示为6（12+22+32+42）。我们再观察，发现其高为4、长为9、宽为5，体积又可以表示为4×5×9，即公式中的4×（4+1）×（2×4+1）。所以6（12+22+32+42）=4×（4+1）×（2×4+1）。

我们如果将小正方体的数量增加至n个，n≥4，按照图1—图6 的方式拼接，最后可以得到一个高为n、长为（2n+1）、宽为（n+1）的长方体，该长方体的体积可以表示为n（n+1）（2n+1），又可以表示为6（12+22+32+…+n2），所以12+22+32+…+

方法二

我们仍然先来验证12+22+32+42的结果。图7中的立方体表示12+22+32+42。

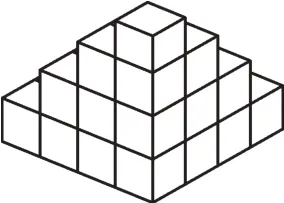
图7

我们准备三个这样的立方体，如图8，将这三个立方体拼接到一起，得到图9。

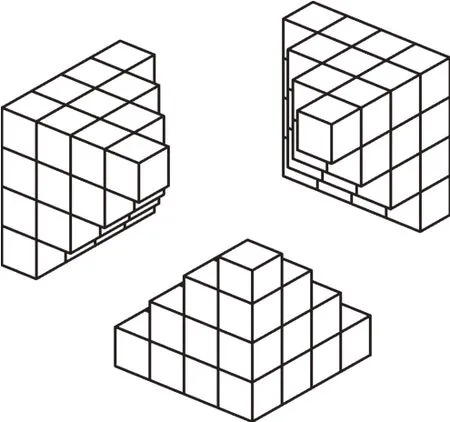
图8

图9

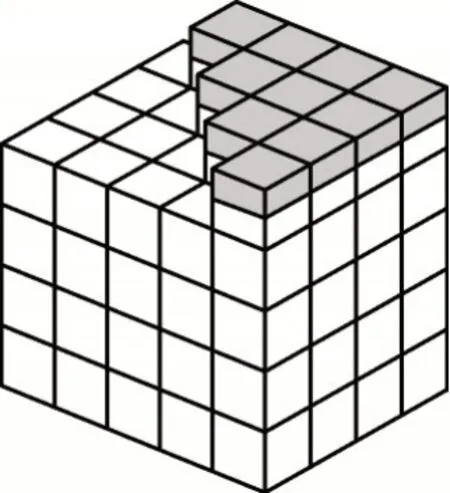
图10

如图11，将横切下来的小立方体整体补位在图10 的最上一层，正好得到一个长方体。其长为5、宽为4、高为体积可以表示为5×4×（4+。该长方体的体积又等于3（12+22+32+42），即3（12+22+32+42）=5×4×（4+，即6（12+22+32+42）=5×4×（8+1）=4×（4+1）×（2×4+1）。

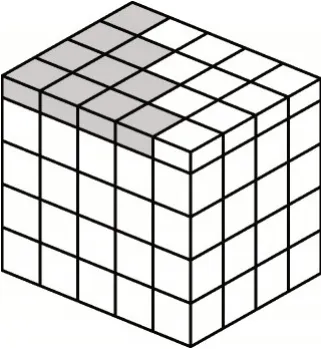
图11

我们如果将小正方体的数量增加至n个，n≥4，按照图7—图11 的方式拼接，最后可以得到一个宽为n、长为（n+1）、高为（n+的长方体，该长方体的体积可以表示为n（n+1）（n+，又可以表示为3（12+22+32+…+n2），所以12+22+32+…+n2=

以上两个图形的证明方法是不是给你豁然开朗的感觉？请同学们动动脑筋，思考还有没有其他证明方法。