基于离散元法的SLM 刮刀倾角对粉末铺展行为的影响研究1)
李 雯 刘其鹏 , 高月华 楚锡华 张 昭 王振军
* (南昌航空大学江西省航空构件成形与连接重点实验室,南昌 330063)
† (武汉大学土木工程学院,武汉 430072)
** (大连理工大学工程力学系,辽宁大连 116024)
引言
选区激光熔化(selective laser melting,SLM)作为增材制造技术的一种,在复杂结构制造、个性化定制等方面具有独特优势,在航空、航天等领域有巨大的应用空间和发展前景[1-2].SLM 的原理是通过刮刀等铺粉装置将粉末铺展在工作面上,在高能激光束作用下选择性熔化,通过铺粉-熔化的循环过程形成最终零件.制造质量要求粉层致密而均匀,但由于颗粒、工艺和设备等的影响,粉层会出现空斑、偏析等缺陷[2],进而使沉积层出现孔隙、材料分布不均、精度不足等缺陷[3],因此需要研究铺粉过程中的粉末流动行为,优化工艺参数,提高粉层铺展质量.
粉堆是一个典型的离散系统,其铺展后的堆积密度、结构均匀性等取决于每个颗粒的运动状态.通过高速摄相等试验手段可以获得铺展过程中粉堆的形貌,但难以获得所有颗粒的详细运动信息,包括速度、轨迹和接触力等,亦不能对颗粒的堆积质量进行有效测量与评估.目前,针对铺粉过程粉末流动行为的研究主要采用基于离散单元法(discrete element method,DEM)的数值模拟途径[4-20].离散单元法基于牛顿第二定律描述每个颗粒的运动,详细计算颗粒之间的相互作用力,能够反映大量颗粒材料的流动行为,深入再现粉末铺展过程中颗粒的运动规律及特征,以及颗粒之间、颗粒和设备间的相互作用,已成为预测和分析SLM 粉床铺展行为的有效方法.
影响粉末铺展行为的因素主要有颗粒性质、工艺参数和铺粉设备3 个方面.对于粉末颗粒性质,主要集中于颗粒尺寸及分布、摩擦系数、黏附力等的研究.Chen 等[4-5]研究表明,适当减小粒径、降低滑动和滚动摩擦系数能够提高粉末颗粒的流动性.Meier 等[6-7]讨论了黏附力在DEM 模拟中的影响,表明考虑黏附力的模型能更好地反映粉末的流动行为.对于工艺参数,文献[8-10]研究了铺粉速度和间隙高度对粉层密度、配位数和表面粗糙度的影响,Nan 等[11]分析了铺粉速度和间隙高度对剪切带演化和质量流量的影响.
铺粉设备的影响主要体现在刮刀和基板与颗粒间的相互作用.基板作为静态墙主要通过粗糙度影响颗粒的铺展,Xiang 等[12]发现粗糙基板表面会阻碍颗粒运动并影响粉床填充质量,冯一琦等[13]发现粗糙基板上的粉层致密性更好,孙远远等[14]深入分析了粗糙度对粉层内力链结构的影响.刮刀几何特征也会显著影响颗粒的铺展行为,已有学者对该问题开展了一些研究工作.Zhang 等[15]和陈辉等[16]通过DEM 模拟分析了刮刀和辊子对粉堆作用的不同.Wang 等[17]基于DEM 模拟了倾角45°和135°刮刀、垂直刮刀和圆刮刀的铺粉情况,发现倾角45°刮刀和圆刮刀形成的粉层更致密.Wu 等[18]发现三角形刮刀端部的刮擦作用易使颗粒发生飞溅,从而降低粉层均匀性.Cheng 等[19]研究发现刮刀倾斜可使粉末压力和压实度增强,从而形成更致密的粉层.Yao 等[20]对均一粒径粉堆在刮刀倾斜时的铺展行为进行了模拟分析,发现颗粒通过间隙时可以被倾斜表面压缩,但倾角超过一定范围会产生较强的力拱,影响颗粒的流动性.以上诸多学者的研究贡献表明,刮刀倾斜角度对粉末铺展行为有较大影响,但刮刀倾角对粉末铺展性能的影响规律及内在机理的分析不够充分,仍需进一步研究.
研究铺粉过程中粉末流动行为时通常将颗粒划分为不同区域.如Chen 等[4]基于颗粒相对于刮刀的速度分布特征,定义了剪切线,并将剪切线上方粉末分为斜坡快速运动区和其余的慢速运动区.Zhang等[15]根据颗粒的流动行为及接触力特征,将粉堆分为雪崩区、慢流区和准静态区.这些区域划分有助于理解铺粉过程中颗粒的流动规律,然而,以上划分方式均针对垂直刮刀情况,当刮刀倾斜时,刮刀前方颗粒的运动特征发生变化,相应的区域划分亦需进一步探讨.
本文基于LIGGGHTS 软件,建立粉末铺展过程的DEM 模型,对不同刮刀倾角(角度变化范围-60°~60°)时的粉末铺展动力学过程进行仿真,探讨倾角对粉层铺展质量的影响规律.构建了一个粉层质量综合评价指标,对粉层致密度和均匀性进行综合评估.提出了一个新的颗粒分区方案,将颗粒体系划分为底层区、斜坡区、刮刀影响区和内部区4 个区域,分析不同区域颗粒的运动轨迹、速度场,以及颗粒间接触力的特征,研究刮刀倾角对粉末流动行为影响的内在机理.为优化SLM 工艺参数、提高沉积质量提供理论基础.
1 研究方法
1.1 离散元方法
在给定的外力或位移驱动下,系统内各个颗粒间会产生力和力矩的作用,根据牛顿第二定律,单个颗粒的运动方程可表示为
式中,mp和Ip分别为颗粒p 的质量和转动惯量,xp和 θp分别为颗粒p 的线位移和角位移,是作用在颗粒p 上的外力及外力矩,分别表示颗粒q 作用在颗粒p 上的法向和切向接触力,Mpq表示接触矩,一般认为接触矩包含切向力产生的矩和滚动阻矩两部分.
DEM 中颗粒间的法向和切向接触力通常由Hertz-Mindlin 模型[21-22]描述,其中,法向接触力还需要考虑粉末颗粒间黏附力的影响,一般采用JKR 模型[23],滚动阻矩一般采用恒定阻矩模型[17,20,24],相应的接触力及力矩表达式为
式中,E*为等效弹性模量,R*为等效半径,a为接触半径,γp为颗粒p 的表面能密度,m∗为等效质量,ζ为阻尼比,与恢复系数e有关,G∗为等效剪切模量,为切向重叠,分别为法向和切向等效刚度,分别为法向和切向相对速度,µs为滑动摩擦系数,npq和tpq分别为法向和切向单位向量,µr为滚动摩擦系数,为相对角速度向量.
1.2 铺粉模型
铺粉模型如图1 所示,基板长L=15 mm,宽W=0.5 mm,刮刀宽度与基板宽相等.粉末粒径分布D10=25 μm,D50=40 μm,D90=65 μm,考虑到气雾化法制备的粉末颗粒球形度较高,因此模型中颗粒简化为球形[5].间隙高度H=1.5D,铺粉速度v=0.03 m/s,模拟域大小为16 mm×0.5 mm×10 mm,其中,为了减少参与计算的颗粒数量,提高计算效率,在y方向设置了周期性边界条件.图2 为不同倾角的刮刀模型示意图,角度取值分别为θ=-60°,-45°,-30°,0°,30°,45°,60°,不同刮刀高度和宽度相同(b=3 mm,w=0.5 mm).
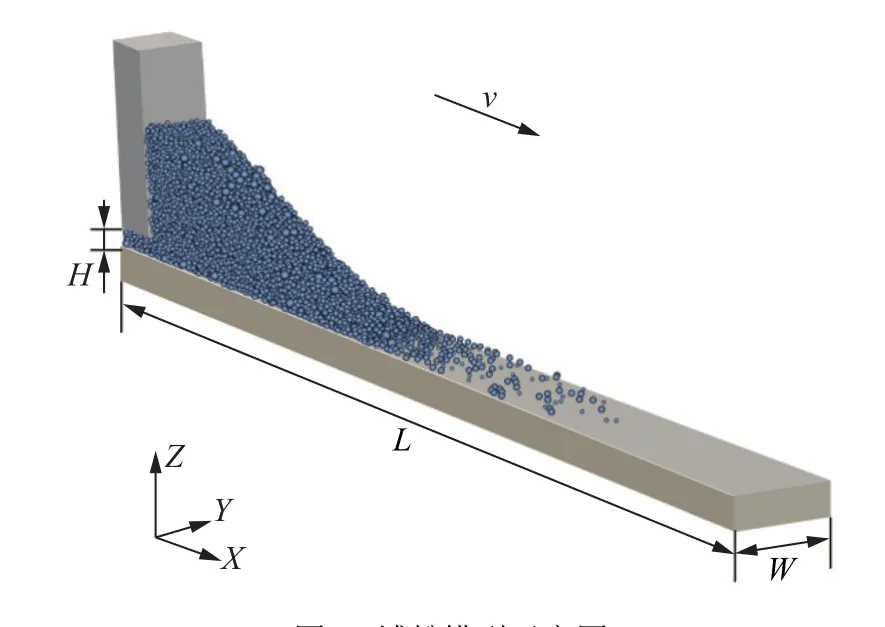
图1 铺粉模型示意图Fig.1 Schematic of powder spreading model
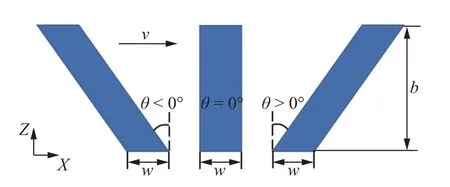
图2 不同倾角的刮刀模型示意图Fig.2 Blade models with different inclination angles
316L 不锈钢粉末材料参数见表1,其中,弹性模量E的实际值为220 GPa,在不影响模拟结果的前提下为了减少计算时长[11],对其缩小了100 倍;颗粒与壁面之间除滑动摩擦系数不同外,其余参数均与颗粒间参数相同;时间步长Δt的取值范围在瑞利临界时间步长的20%~80%之间[4].
1.3 模型验证
通常采用休止角试验验证离散元数值模型的合理性与有效性[25-26].休止角实验结果参考文献[27],模型如图3(a)所示.为提高计算效率,模拟时通常通过缩小漏斗口直径和底板尺寸,减少计算的颗粒数量,已有研究者讨论了缩小休止角模型尺寸的合理性[6,9].此外,模拟过程中向下移动底板来限制粒子的下落高度以减小颗粒下落冲击/惯性效应的影响[6].
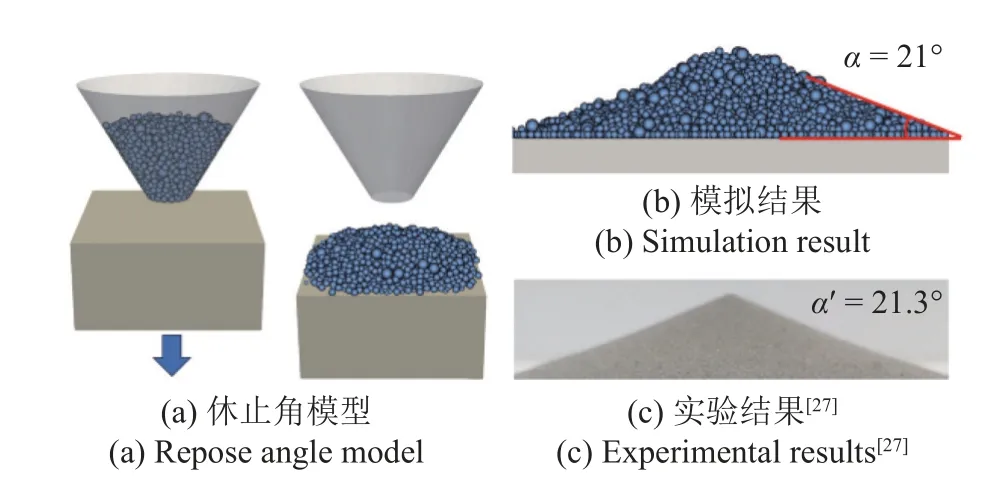
图3 316L 粉末休止角模型及结果对比Fig.3 Repose angle modeling and results comparison for 316L powders
本文模型验证结果如图3(b)和3(c)所示,模拟所得休止角为21°,而文献[27]中实验所得休止角为21.3°,二者一致性很好,表明所建立颗粒模型及参数取值是合理的.
1.4 粉层铺展质量指标
粉层铺展质量通常采用致密度和均匀性两个指标度量.致密度可用颗粒堆积密度 ρ 表征[20],定义为测量区域内颗粒所占体积与区域体积之比,即
其中,z(x) 为任一位置高度hb与测量区域平均高度的垂直偏差,即.为了便于统计计算,对式(7)进行离散化,表示为
其中,n为测量区域内划分的离散区域个数.
2 不同刮刀倾角时的粉层铺展结果
不同刮刀粉层稳定阶段(粉层中部L/3 段)的颗粒分布如图4 所示,图5 为不同倾角刮刀铺展后的粉层堆积密度和表面粗糙度变化曲线.
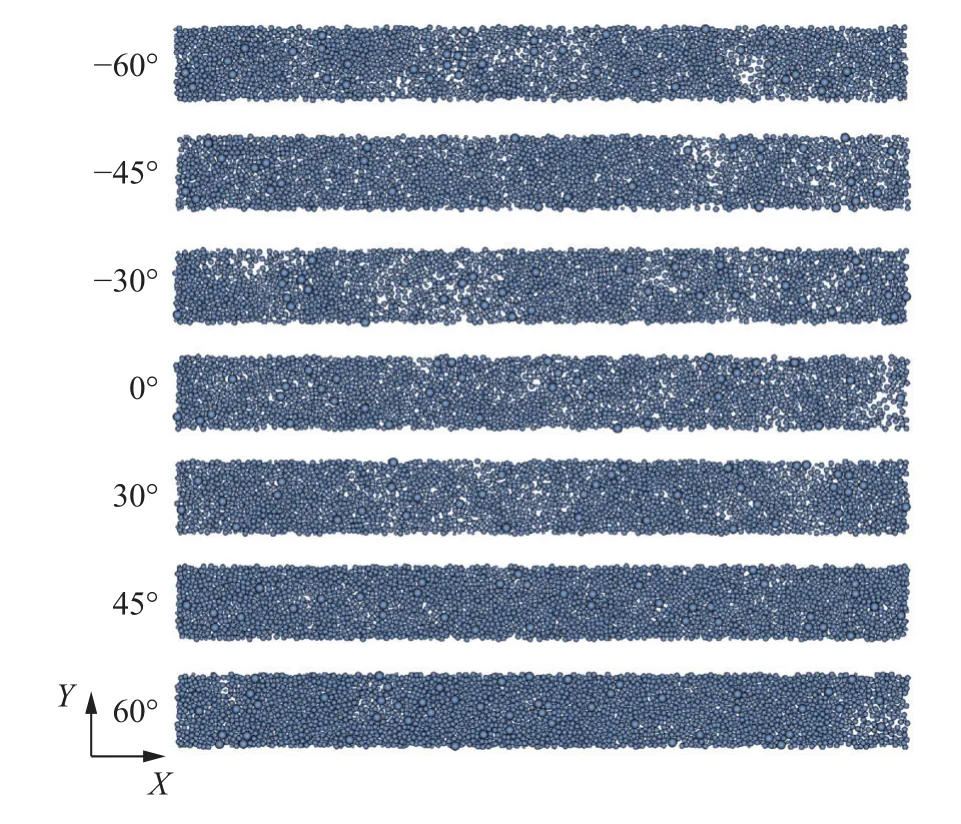
图4 不同倾角刮刀铺展结果对比Fig.4 Comparison of spreading results of blades with different angles
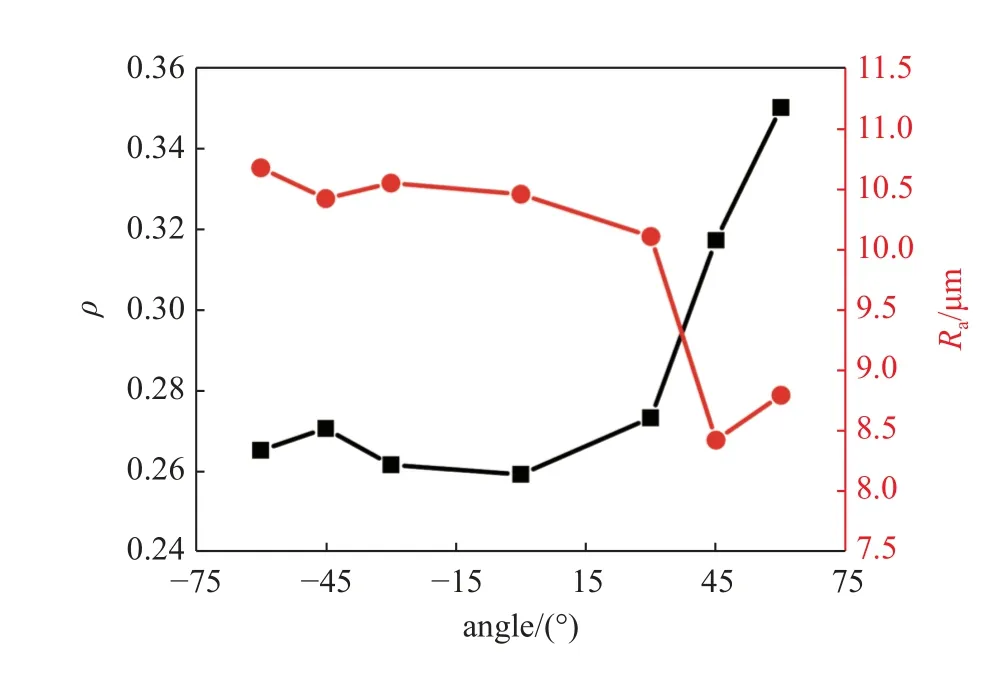
图5 粉层堆积密度和表面粗糙度随刮刀倾角变化曲线Fig.5 Curve of powder layer packing density and surface roughness with blade inclination angle
由图4 可知,当刮刀倾角θ≤0°时,粉层存在大量空斑,当θ>0°时,粉层的空斑比例随着倾角的增大而逐渐减小.由图5 可看出,θ≤0°时,不同θ值的堆积密度和表面粗糙度变化很小.而当θ>0°时,随着θ的增大,堆积密度不断增大,也即粉层致密度不断增大.表面粗糙度随着θ的增大先减小(0°<θ≤45°时)而后略有增大(θ>45°时).
现有文献中粉层质量的评价指标一般为两个:致密度和粗糙度(或均匀性).当两个指标变化趋势不一致时,难以对粉层质量进行有效评估.鉴于此,这里尝试提出一个能同时考虑粉层致密度和均匀性的综合质量指标I
其中,R为表征均匀性的归一化指标,表达式为
式中Rmax为粗糙度最大值.通常认为堆积密度影响较为重要,因此式(9)中 α 取值0.8.表2 给出了不同刮刀倾角下的I值.当θ≤0°时,粉层质量指标I值较低且随θ角变化不大;而θ>0°时,粉层质量指标I值随θ角增大而不断升高,在本文所选的刮刀倾角及工艺参数下,60°时粉末层的铺展质量最佳.

表2 不同刮刀倾角时质量指标I 值Table 2 Spreading quality index I at different blade angles
3 粉层铺展的颗粒运动学机理
刮刀倾角的改变影响着粉末颗粒的运动行为,进而决定了粉层的沉积质量.因此,本节对铺粉过程中颗粒的运动特征进行详细分析.根据颗粒分布及运动特征并考虑刮刀倾斜特点,提出一个新的颗粒分区方案,即:将粉堆划分为4 个区域(见图6):底层区(区域I),斜坡区(区域II),刮刀影响区(区域III) 和内部区(区域IV).底层区高度与间隙高度H相同;斜坡区由自由向下运动的颗粒组成,宽度约为3D;刮刀影响区为刮刀前方平行于刮刀的区域,宽度约为2D~5D.

图6 粉堆颗粒分区示意图Fig.6 Partition scheme of particle heap
3.1 颗粒运动轨迹
图7 为不同时刻不同区域内的颗粒运动轨迹.由图7 可以看出,底层区(白色区域I)的颗粒运动到刮刀后方,沉积于基板上.斜坡区(红色区域II)内的颗粒受重力作用沿斜坡向下运动,到基板附近后进入底层区.刮刀影响区(蓝色区域III)颗粒运动轨迹与刮刀倾角有关.当θ<0°时,大部分颗粒堆积在刮刀前方,且θ值越小,堆积越严重.当θ≥0°时,该区域大部分颗粒向上运动进入斜坡区,且随着θ的增大,颗粒更快地进入斜坡区.刮刀影响区、斜坡区和底层区形成了粉堆的外围区.刮刀倾角不同,外围区的运动模式不同.当θ<0°时,由于刮刀影响区的颗粒堆积,仅是斜坡区的颗粒滑落沉积模式;当θ≥0°时,刮刀影响区和斜坡区的颗粒运动连续,并与底层区形成了顺时针方向的整体环流运动模式.

图7 不同刮刀倾角铺粉过程中颗粒的运动轨迹Fig.7 The particle trajectories during powder spreading with different blade angles
内部区域(白色区域IV)的颗粒较多,为深入分析该区域的颗粒运动,选取两部分进行标记,上层部分为绿色,下层部分为黄色.当θ<0°时,该区域颗粒运动主要为下落沉积.当θ≥0°时,该区域的大部分颗粒呈现出明显的顺时针环流运动,且随着θ的增大,更多的颗粒进入斜坡区,进而参与整体的环流运动.
3.2 颗粒运动速度分布
不同倾角刮刀铺粉过程中颗粒相对于刮刀的速度矢量分布如图8 所示.可以看出,底层区的颗粒速度最大,且方向与刮刀前进方向相反.不同刮刀倾角时,斜坡区的颗粒都具有沿斜坡向下的速度,说明该区域颗粒向下滑落运动.刮刀影响区的颗粒速度受刮刀倾角的直接影响.当θ<0°时,颗粒具有沿刮刀面向下的速度,说明颗粒沿刮刀面下落运动,与斜坡区的颗粒运动相似.当θ≥0°时,该区域的颗粒有沿刮刀面向上的速度,说明颗粒向上运动,填补斜坡区颗粒滑落留下的空隙,进而形成颗粒粉堆外围的环流运动.内部区的颗粒在不同刮刀倾角时均存在内部环流运动,θ=0°时内部环流运动范围最大,随着倾斜角度|θ|的增大,内部环流运动减弱、范围减小,更多的颗粒开始参与外围的颗粒运动.
综合分析颗粒运动轨迹和颗粒运动速度可知,当θ<0°时,粉堆颗粒运动呈下落模式;当θ≥0°时,粉堆颗粒运动呈整体环流模式,且整体环流运动随着θ的增大而愈加充分.因此,θ>0°的刮刀能够充分调动粉堆所有颗粒发生整体的循环运动,从而使更多颗粒流入间隙,有利于颗粒的沉积.
3.3 刮刀前方剪切带
刮刀前方颗粒的前进速度随高度的升高而逐渐增大,在达到一定高度时接近刮刀速度并趋于稳定.在颗粒前进速度随高度升高而增大的区域,颗粒发生剪切流动形成了剪切带.剪切带范围越大流向刮刀后方的颗粒越多,沉积层的堆积密度就越高[29-31].本节详细分析刮刀倾角对剪切带的影响.
图9 给出了不同倾角时刮刀前方6D×2D范围内的颗粒在x方向上的速度变化曲线,图中速度为归一化处理后的数据.
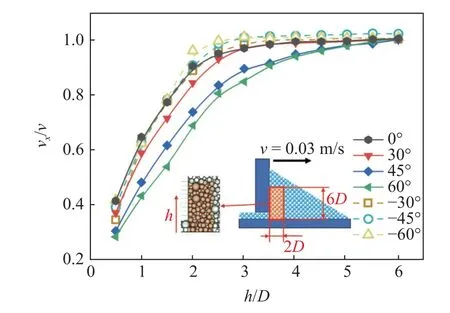
图9 刮刀前方颗粒速度分量vx 分布曲线Fig.9 Distribution curve of particle velocity component vx in front of the blade
由图可知,当θ≤0°时,vx在h=2.5D处达到平稳,颗粒体系的剪切带高度较低(仅为2.5D),且高度随θ的变化不大.因此,θ≤0°时沉积层的堆积密度较小,随θ的变化也不大.当θ=30°时,vx在h=3D处速度达到平稳,θ=45°,60°时,vx在h=5D处达到平稳.与θ≤0°时相比,θ>0°时颗粒体系的剪切带高度较高,且随着刮刀倾角的增大,剪切带高度逐渐增大,向刮刀后方沉积的颗粒逐渐增多.因此,θ>0°时沉积层的堆积密度较大,且随刮刀倾角的增大而增大.
3.4 底层区颗粒速度变化
底层区颗粒在刮刀前方时受刮刀推力作用具有前进方向的速度,而当颗粒运动到刮刀后方时速度逐渐减小,最终静止沉积于基板上.底层区颗粒的速度越小,颗粒越易于沉积.因此,底层区颗粒沉积前后的速度变化也影响着沉积质量.图10 给出了不同刮刀倾角时底层20D×1.5D范围内颗粒沿x方向的速度变化曲线,图中速度为归一化处理后的数据.
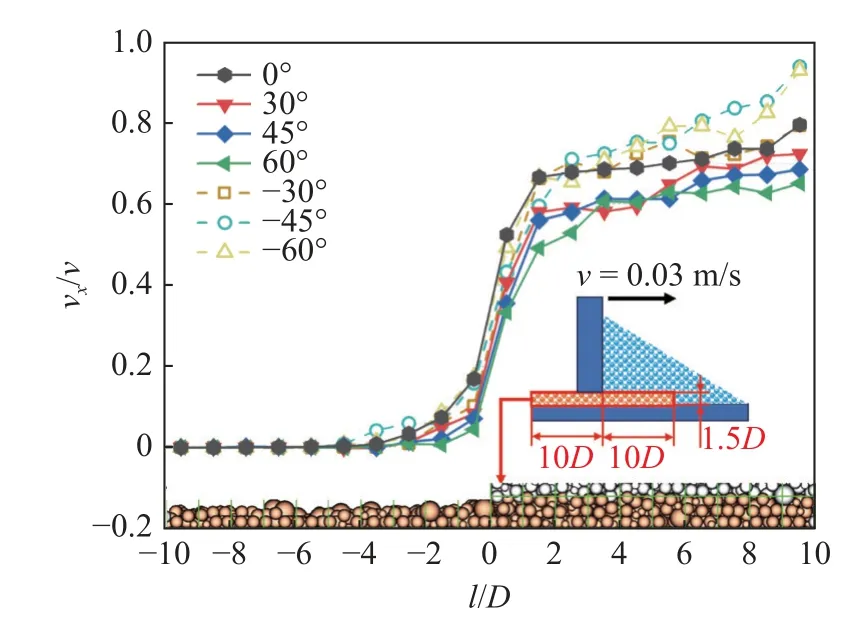
图10 刮刀底层颗粒速度分量vx 分布曲线Fig.10 Distribution curve of particle velocity component vx at the bottom layer below the blade
由图10 所示,在l=-10D~-3D区域,颗粒速度几乎为零,说明此范围内的颗粒已稳定沉积于基板上.在l=-3D~0 区域,该区域内颗粒虽已位于刮刀后方,仍存在微小速度.一方面是由于颗粒受到惯性作用能够继续移动,另一方面是由于位于刮刀底部的颗粒受到刮刀的拖曳作用而发生运动[29].在l=0~2D区域,颗粒开始受到刮刀推力的影响而向前运动.随着与刮刀距离的增加,颗粒速度急剧增大.在l=2D~10D区域,颗粒速度较大,且随着与刮刀距离的增加颗粒速度缓慢增大.不同倾角对底层颗粒速度的影响主要体现在刮刀前方的颗粒速度缓慢增大区(l=2D~10D).随着刮刀倾角的增大,刮刀前方颗粒的速度减小.这与倾斜刮刀对颗粒的压力大小有关,随着刮刀倾角的增大,刮刀对颗粒的压实作用越大,颗粒间的接触力越大,摩擦阻力越大,因此速度越小.
4 颗粒间接触力链
在铺粉过程中,粉末颗粒在重力和刮刀施加的外力作用下相互挤压摩擦,形成了复杂的力链结构,少数颗粒承受较强的力,形成强力链,而大部分颗粒之间的接触力较小,形成弱力链[32].随着刮刀的运动,颗粒体系中的力链不断发生断裂与重组,产生了复杂的流动行为.本节对不同倾角刮刀铺粉过程中颗粒间接触力链的分布及其演化特征进行分析,进一步探讨颗粒流动行为的内在动力学机理.
图11 为不同倾角刮刀铺粉过程中的力链结构.可以看出,强力链主要分布于刮刀间隙前方区域,包括底层区靠近间隙的区域、内部区的下层区域和刮刀影响区的下半部分.当θ≤0°时,颗粒体系的强力链较少.当θ>0°时,随着刮刀倾角的增大,强力链增多,说明刮刀对颗粒的压实作用增强,有利于提高粉床致密度.

图11 不同倾角刮刀铺粉过程中的力链Fig.11 Force chain during powder spreading process with different blade angles
弱力链主要分布于刮刀影响区和内部区的上部.当θ≤0°时,刮刀影响区上部颗粒的弱力链密集,内部区上部弱力链稀疏.这是因为刮刀影响区上部存在颗粒堆积现象,而内部区上部颗粒参与了环流运动.当θ>0°时,粉堆的整体环流运动随刮刀倾角的增大而增强,因此弱力链也随着刮刀倾角的增大越来越稀疏.
在铺粉过程中,随着颗粒的运动,力链不断发生断裂与重组,因此粉堆的接触力是动态变化的.图12给出不同刮刀倾角铺粉过程中粉堆平均接触力随时间的变化曲线.可以看出,随着刮刀倾角的增加,接触力增大,这进一步说明了刮刀倾角越大,刮刀对颗粒的压力及压实作用越大.此外,每条曲线中都存在几处峰值,此时颗粒体系中形成了突增的强力链并发生断裂,可能会引发颗粒堵塞.
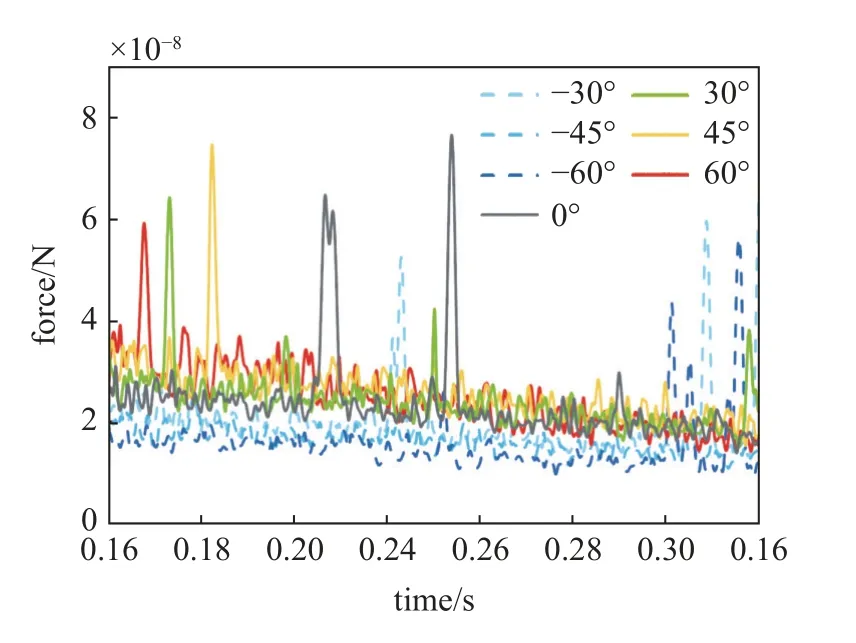
图12 不同倾角刮刀铺粉过程中平均接触力随时间的变化Fig.12 Average contact force variation with time during powder spreading process with different blade angles
图13 给出了θ=0°时强力链突增时刮刀间隙前方的力链和颗粒速度分布.由图可知,刮刀间隙前方的强力链较少,力链呈拱形分布,形成了力拱.由图13(b)可以看出,在力拱存在期间,出现了颗粒堵塞,刮刀前方颗粒难以流入刮刀间隙,导致刮刀下方颗粒稀疏并形成空缺,这将会降低沉积层的致密度和均匀性.
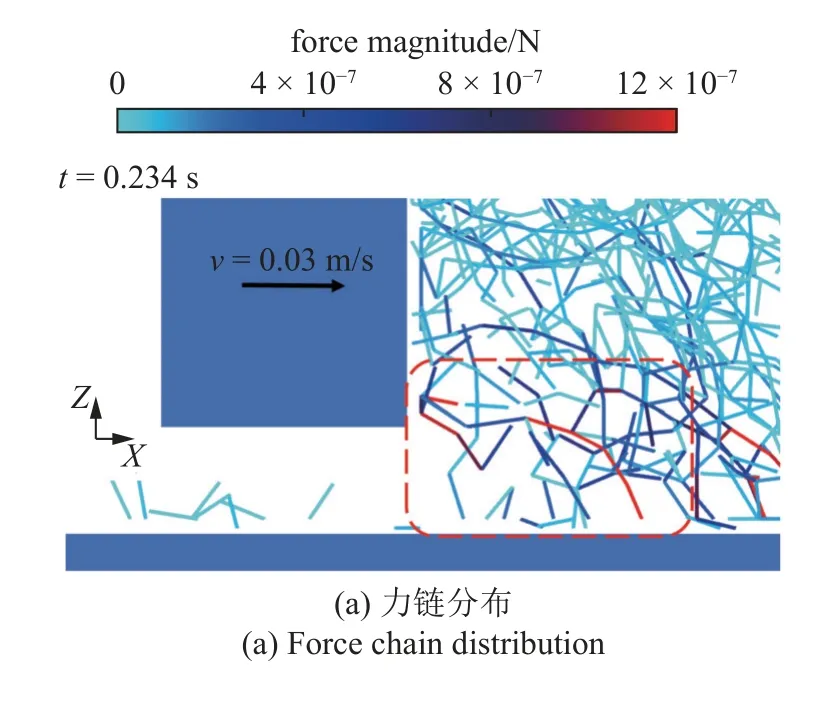

图13 θ=0°强力链突增时刮刀间隙前方的力链和颗粒速度分布Fig.13 Force chain and particle velocity distribution in front of blade when strong chains suddenly increase with θ=0°
图14 给出了θ=60°强力链突增时刮刀间隙前方的力链和颗粒速度分布.由图可知,在刮刀压实作用下,刮刀间隙前方的强力链明显增多,最强力链出现在刮刀下方的底层区.虽然在刮刀间隙前方形成较多的强力链,但这些强力链颗粒在颗粒体系环流运动的影响下会快速变化,因此刮刀间隙前方不会发生颗粒阻塞.刮刀间隙流入了大量颗粒,颗粒层厚度达到了刮刀间隙尺寸,将形成较为致密的沉积层.在刮刀拖曳作用下,间隙底部颗粒形成强力链,部分与刮刀接触的颗粒随刮刀向前运动,使底层颗粒形成局部空缺,对沉积层的均匀性略有影响.
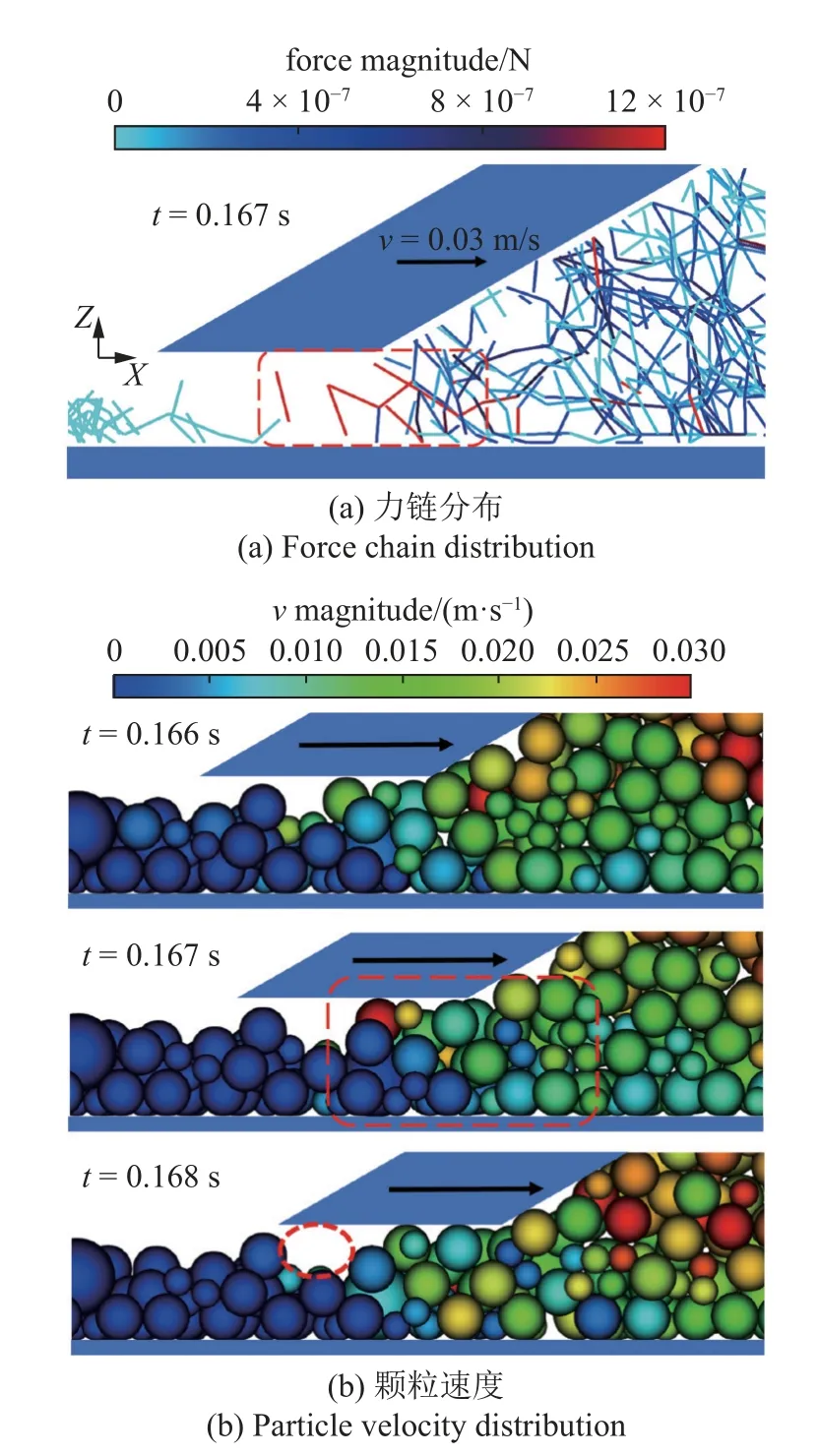
图14 θ=60°强力链突增时刮刀间隙前方的力链和颗粒速度分布Fig.14 Force chain and particle velocity distribution in front of blade when strong chains suddenly increase with θ=60°
5 结论
本文基于离散单元法建立316L 不锈钢粉末选区激光熔化铺粉过程的数值模型,对多个倾斜角度刮刀铺粉过程的粉末动力学行为进行仿真.深入分析了刮刀倾角对粉末铺展质量和流动行为影响的规律及内在机理,得出主要结论如下.
(1) 对比了不同刮刀倾角模型的铺展质量,在θ≤0°时,沉积层表面存在大量空斑,粉层的堆积密度较小,均匀性较低;在θ>0°时,粉层空斑减少,随着θ的增大,粉层的堆积密度逐渐增大,而均匀性先升高后略有降低.综合量化指标评估显示,θ=60°时,粉层质量最佳.
(2) 综合分析颗粒运动轨迹和颗粒运动速度可知,当θ<0°时,粉堆颗粒运动呈下落模式;当θ≥0°时,粉堆颗粒运动呈整体环流模式,且整体环流运动随着θ的增大而愈加充分.因此,θ>0°的刮刀能够充分调动粉堆所有颗粒发生整体的环流运动,从而使更多颗粒流入间隙,有利于颗粒的沉积.
(3) 与θ≤0°时相比,θ>0°时颗粒体系的剪切带高度较高,且随着刮刀倾角的增大该高度逐渐升高,使得向刮刀后方沉积的颗粒逐渐增多,沉积层的堆积密度逐渐增大.
(4) 强力链主要分布于刮刀间隙前方区域.当θ≤0°时,颗粒体系的强力链较少,刮刀间隙前方的强力链易形成力拱引发颗粒堵塞,导致刮刀下方颗粒稀疏并形成空缺,降低沉积层的致密度和均匀性.当θ>0°时,随着刮刀倾角的增大,强力链增多,刮刀对颗粒的压实作用增强.在颗粒体系环流运动的影响下大量颗粒流入刮刀间隙,能够形成致密度较高的粉床.
(5) 本文在铺粉速度0.03 m/s、间隙高度1.5D的条件下获得了刮刀倾角对铺粉过程的影响规律.然而,当铺粉速度或间隙高度改变时,颗粒的流动行为也会发生变化,相应地,不同刮刀倾角对颗粒影响规律可能会有所不同.因此,后续研究中还需进一步考虑上述两个因素的影响.

