一类非线性系统的广义伴随线性方程分析研究1)
张 波 张文博 彭志科 ,†,
* (宁夏大学机械工程学院,银川 750021)
† (上海交通大学机械系统与振动国家重点实验室,上海 200240)
引言
频率响应函数是刻画线性系统的一个基本概念,它是经典控制论和系统设计的理论基础,在工程实践中已得到了广泛应用[1].考虑到利用频率响应函数对线性系统分析带来的独特优势,一些学者基于Volterra 级数理论,将线性系统中频率响应函数的概念拓展到了非线性系统中,其中广义频率响应函数(generalized frequency response functions,GFRFs)是非线性系统中各阶Volterra 核函数的多维傅里叶变换[2].广义频率响应函数是描述非线性系统频域特性的一系列多维函数,非线性系统的第一阶广义响应函数与其线性派生系统的频率响应函数相同.从20 世纪70 年代初以来,广义频率响应函数已经应用于非线性系统的频率特性研究,如频率响应的谐波特性、增益压缩扩张特性和相互调制特性等[3];在机械工程和生物工程等领域中广义频率响应函数也用于分析系统的非线性特性[4-6].由于广义频率响应函数的多维特性,导致高阶广义频率响应函数物理意义难以理解,同时高阶广义频率响应函数也不易被直观表示出来,这些因素限制了广义频率响应函数在实际工程应用中的发展.为了解决这个问题,在过去的几十年里,人们提出了几种非线性系统的一维频域表示方法.例如Lang 等[7-8]提出的非线性输出频率响应函数(nonlinear output frequency response functions,NOFRFs)、非线性系统的输出频率响应函数(output frequency response function,OFRF)以及Rijlaarsdam 等[9]提出的高阶正弦输入表示函数(higher order sinusoidal input describing functions,HOSIDF).已有研究表明,输出频率响应函数用于在频域中对非线性系统的设计[10-11],高阶正弦输入描述函数用于研究受正弦输入影响的非线性系统[12].而非线性输出频率响应函数则是一系列关于频率的一维函数,它对非线性系统频域分析提供了一系列类似于伯德(Bode)图的频域表示方法.此外,基于非线性输出频率响应函数的非线性系统分析包括对所研究的非线性系统的非线性输出频率响应函数进行计算,用非线性输出频率响应函数作为相关指标来揭示系统的动态特性[13-14].目前,非线性输出频率响应函数已经成功应用于工程结构系统的状态监测和故障诊断[15-24].
研究表明,利用非线性输出频率响应函数进行非线性系统分析及结构损伤检测的关键是如何准确计算出系统的各阶非线性输出频率响应函数.目前,有关非线性输出频率响应函数的计算方法大多数是基于系统的非线性输出频率响应函数对输入激励幅值变化不敏感性的原理进行计算,即对系统进行多次相同频率不同幅值的激励,得到系统输出响应后利用最小二乘法(least squares method,LSM)计算出系统的各阶非线性输出频率响应函数.而在用最小二乘方法计算非线性系统的高阶非线性输出频率响应函数时,往往需要输入激励次数不小于系统的截断阶数,而且在结构损伤检测中大多采用离线检测的方式.此外,Feijoo 等[25]提出了非线性系统伴随线性方程(associated linear equations,ALE)的概念,Bayma 等[26]根据伴随线性方程提出了基于带外部输入的非线性自回归模型(nonlinear auto regressive with eXogenous input,NARX)非线性输出频率响应函数的计算方法,但该方法计算过程中涉及丢番图方程的求解问题,同时由于伴随线性方程法仅适用于非线性项为输入激励或输出响应多项式的非线性系统,所以无法求解含有输入激励或输出响应导数项的非线性系统,如范德波尔系统等.最近,Zhu等[27]提出了基于NARX 模型表示的广义伴随线性方程法(generalized associated linear equations,GALEs),并且将该方法应用于机床刀具损伤状态监测及火车车轮疲劳损伤的在线检测.
从非线性系统频域分析的研究情况来看:关于非线性输出频率响应函数的计算方法大多数基于最小二乘法.虽然伴随线性方程法可以准确地计算出非线性系统任意阶非线性输出响应,但其适用范围却有很大局限性,所以进一步研究伴随线性方程是利用非线性输出频率响应函数进行非线性系统分析与结构损伤检测的基础.本文基于非线性微分方程(nonlinear differential equation,NDE)模型表示的非线性系统广义频率响应函数递归计算公式及Volterra级数理论,对由NDE 模型表示的一类非线性系统的广义伴随线性方程进行研究,采用数值计算的方法对这类非线性系统的非线性输出频率响应函数进行分析.同时,利用线性算子理论对非线性系统中典型非线性效应的产生机理进行研究,为利用非线性输出频率响应函数进行结构损伤检测及非线性系统的分析和设计提供了一种有效途径.
1 非线性系统NDE 模型的广义伴随线性方程
1.1 广义频率响应函数
根据Weierstrass 函数逼近理论[28],在封闭且有界区间上,任何连续函数都能用一组多项式函数来对其进行任意精度的一致逼近,所以工程实际中的许多非线性系统都可以描述为如下多项式型非线性系统[29-30]
式中,u(t) 为系统的输入,y(t) 为系统的输出,p+q=n,Cp,q(l1,l2,···,lp+q) 为多项式系数,N为u(t) 与y(t)的最大非线性阶数,L为微分的最大阶数,求和符号为
微分算子 D 定义为
针对由式(1)所描述的系统,当系统输入是具有实际物理意义的信号u(t) 时,该系统可产生确定的输出响应y(t),且系统必定存在非零线性输出系数,即C1,0(0)≠0 .若由NDE 模型表示单输入单输出非线性系统,则式(1)可以表示为
式中,等式右边Cp,q(l1,l2,···,lp+q) 满足条件:C1,0(0)∉Cp,q(l1,l2,···,lp+q) .
若式(4)表示的系统在零平衡点渐近稳定,则该系统的输出y(t) 可以用Volterra 级数表示为
式中,u(t) 为系统的输入,y(t) 为系统的输出,yn(t) 为系统的n阶非线性输出响应,hn(τ1,τ2,···,τn) 为非线性系统的n阶广义脉冲响应函数或n阶Volterra 核函数,N为Volterra 级数的截断阶数.对式(5)做傅里叶变换(Fourier transform,FT)后可得[31]
式中,Y(jω) 为系统输出y(t) 的傅里叶变换,U(jω) 为系统输入u(t) 的傅里叶变换,Yn(jω) 为系统的n阶非线性输出响应yn(t) 的傅里叶变换.Hn(jω1,jω2,···,jωn)为系统n阶Volterra 核函数hn(τ1,τ2,···,τn) 的n维傅里叶变换,被称为广义频率响应函数.式(6) 中为被积函数在n维超平面 ω1+ω2+···+ωn=ω 上的多重积分.
Billings 等[29]根据谐波探测法推导出了由NDE 模型表示的计算非线性系统广义频率响应函数递归表达式
式中,LN=(l1,l2,···,lp+q) 为与Cp,q(l1,l2,···,lp+q) 相对应的系数指标.
1.2 非线性输出频率响应函数
由式(6)可知非线性系统的广义频率响应函数是多维函数,各阶广义频率响应函数的维数等于它的阶数,由于广义频率响应函数的阶数超过3 阶以后很难直观表示出来,这对广义频率响应函数在工程中的分析估计造成了极大困难.为了克服这个困难,Billings 等[7]提出了非线性系统的非线性输出频率响应函数的概念.对于单输入单输出非线性系统,非线性输出频率响应函数为
式中,Yn(jω) 为系统的n阶非线性输出频谱,Un(jω)为系统的n阶非线性输入频谱,它是系统输入u(t)的n次幂un(t) 的傅里叶变换,即
图1 表示非线性系统中的各阶非线性输出频率响应函数与系统输入输出的关系,也揭示了线性系统中的频率响应函数与非线性系统中非线性输出频率响应函数之间的关系.即n=N=1 时,Gn(jω)=G1(jω)表示线性系统的频率响应函数.

图1 非线性系统的NOFRFsFig.1 The NOFRFs of nonlinear systems
由式(9)描述的非线性输出频率响应函数的最大特点是一维特性,它是广义频率响应函数在不同加权因子作用下的加权平均值,所以非线性输出频率响应函数对非线性系统在频域的分析带来了极大的便利,这也是非线性输出频率响应函数在结构状态检测及故障诊断等领域受到广泛应用的重要原因.
1.3 NDE 模型广义伴随线性方程
根据NDE 模型的广义频率响应函数递归表达式(7)及非线性输出频率响应函数的定义式(9),在式(7)左右两边同时乘并在n维超平面 ω1+ω2+···+ωn=ω 上积分得:
式(7)左边结果为
式(7)右边结果为
其中,An,u(jω) 为纯输入非线性项,且
式中An,uy(jω) 为输入输出耦合非线性项,且
式中
对式(17)两边同时做傅里叶逆变换得
An,y(jω) 为纯输出非线性项,且
式中,F T[·] 表示傅里叶变换.
分析可知,式(20)在表达形式上与线性系统的频域表达形式类似,可以看作是该线性系统的频率响应函数,Vn(jω) 是该线性系统广义输入的傅里叶变换,继续对式(20)左右两边做傅里叶逆变换得
式中,Vn(t) 是Vn(jω) 的傅里叶逆变换,称为广义输入,TL为线性算子.式(25)称为非线性系统(4)的广义伴随线性方程[27].若在式(25)中已知线性算子 TL与Vn(t),则由NDE 模型描述的非线性系统(4) 的n阶非线性输出响应yn(t) 可以通过求解简单的线性方程得到.从广义伴随线性方程中计算出n阶非线性输出响应yn(t) 后,可由式(11)计算出非线性系统的任意阶非线性输出频率响应函数.
1.4 NDE 模型广义伴随线性方程的推导
对于由NDE 模型所描述的非线性系统(4),由广义伴随线性方程的表达式(13)~式(19)得
式中,n∈N∗,LN=(l1,l2,···,lp+q) 是式(8)中与Cp,q(l1,l2,···,lp+q) 相对应的指标.
式(26)称为由NDE 模型所描述的非线性系统(4)的广义伴随线性方程,比较式(7)与式(26)可知两者在表达形式上相似,并且式(27)中yn(t) 与可以理解为式(7) 中的广义频率响应函数Hn(jω1,jω2,···,jωn) 与在时域中的类比,它揭示了一种关于非线性系统时域与频域的新关系.
通过式(25)与式(26)可得,由NDE 模型表示的非线性系统广义伴随线性方程中的线性算子 TL与广义输出Vn(t) 表达式为
将式(27)代入式(29)可得Vn(t) 的表达式,其中广义输入Vn(t) 是由系统输入激励u(t) 及其各阶微分Dliu(t) 和系统前n-1 阶的输出响应yn-1(t),yn-2(t),···,y1(t) 及其各阶微分 Dliyj(t) 的组合函数.因此,通过求解式(26)表示的广义伴随线性方程后,可得系统(4)的各阶非线性输出响应yn(t) .
1.5 广义伴随线性方程计算非线性输出频率响应函数的步骤
广义伴随线性方程计算系统的非线性输出频率响应函数分为以下3 个步骤:
(1) 将NDE 模型描述的非线性系统改写成式(4)的形式;
(2) 由式(26)表示的广义伴随线性方程求解出系统的各阶非线性输出响应yn(t) ;
(3) 由式(11)计算出系统的各阶非线性输出频率响应函数Gn(jω) .
1.6 非线性输出频率响应函数的递归计算法与耦合计算法
计算NDE 模型的广义伴随线性方程(26)时,由式(25)可知,若广义输入Vn(t) 是由线性算子 TL的本征函数构成的线性组合,则广义伴随线性方程(26)存在解析解.在实际工程系统中,系统的输入激励往往是冲击、随机或非平稳信号,这类输入激励的广义伴随线性方程并不存在解析解,所以需要用数值计算的方法对广义伴随线性方程(26)进行求解.由1.5 节中广义伴随线性方程计算系统的非线性输出频率响应函数的步骤可知,计算非线性输出频率响应函数的关键是计算系统的广义伴随线性方程.
基于NDE 模型的广义伴随线性方程方法计算系统非线性输出频率响应函数的一种方法是:在求解NDE 模型的广义伴随线性方程时,用数值计算(如Runge-Kutta)方法逐阶求解广义伴随线性方程(26)可得系统的各阶非线性输出响应yi(t),根据非线性输出频率响应函数的定义式(11)可计算出系统前N阶的非线性输出频率响应函数,该方法称为递归计算法(recursive computational method,RCM),其计算步骤如表1 所示.
非线性输出频率响应函数的另一种数值计算方法是:在求解NDE 模型的广义伴随线性方程时,将系统的前N阶广义伴随线性方程视为具有坐标耦合的N个线性方程组,用数值计算(如4 阶Runge-Kutta)方法联立求解耦合方程组后得到系统的各阶非线性输出响应yi(t),最后根据非线性输出频率响应函数的定义式(11)计算出系统前N阶的非线性输出频率响应函数,该方法称为耦合计算法(coupled computational method,CCM),其计算步骤如表2 所示.

表2 耦合计算法Table 2 Coupled computational method
2 数值仿真与分析
本节以范德波尔振子为例,利用数值仿真实验对上述理论分析结果的正确性进行验证.针对广义伴随线性方程求解非线性输出频率响应函数的数值计算问题,分析了递归计算法与耦合计算法的计算结果产生差异的原因.最后,以达芬系统为例,通过广义伴随线性方程与线性算子理论分析了达芬系统中典型非线性效应产生的原因.
2.1 范德波尔(van der Pol)系统
范德波尔振子的NDE 模型为[32]
式中,m,c,k为系统的线性参数,CE为系统的非线性参数,u(t) 为系统的输入激励,y(t) 为系统的输出响应.
将式(30)代入式(4)得
将式(31)和式(32)代入式(26)得系统前7 阶广义伴随线性方程为
设系统的参数为:m=1 kg,c=30 N·s/m,k=1.0×104N/m,CE=7.5×106N·s/m3,输入激励
式(30)的解y(t) 与式(33)中各阶广义伴随线性方程的解yi(t) 均由4 阶Runge-Kutta 方法计算得到,其中采样频率f s=1024 Hz .当系统的最大非线性阶数为N时,由式(5)可得系统输出响应yGN(t) 为
图2 所示为Runge-Kutta 法与广义伴随线性方程法计算结果对比.图2(a) 表示最大非线性阶数N取不同值时系统频域响应对比.图2(b)为N=7时,时域响应对比.结果表明,取适当的截断阶数N,广义伴随线性方程能够很好地表示系统的输出响应,从而验证了由NDE 模型表示的非线性系统广义伴随线性方程(26)的有效性.
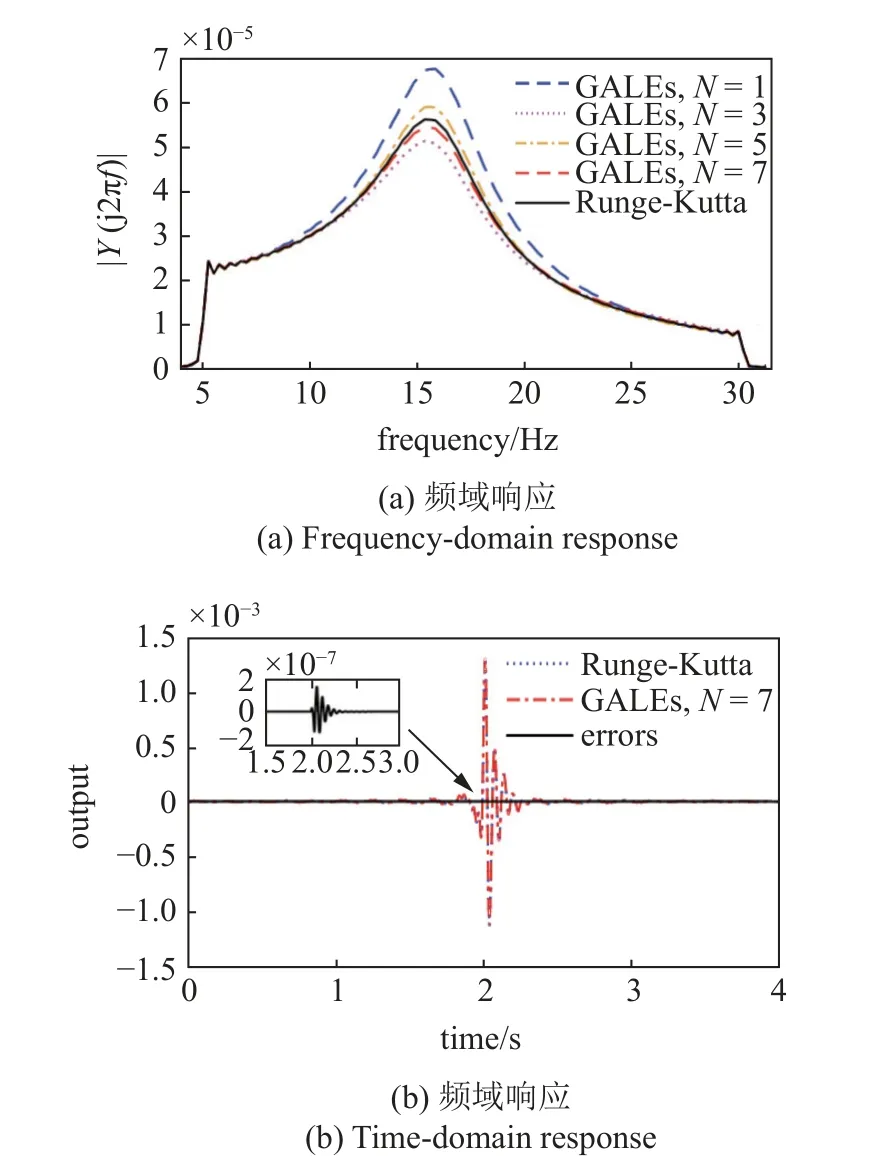
图2 Runge-Kutta 与GALEs 响应对比Fig.2 Comparison of the responses by using Runge-Kutta and GALEs
由式(33)可知,在零初始条件下,范德波尔振子式(30)的第2 阶、4 阶和6 阶广义伴随线性方程的解y2(t),y4(t),y6(t) 为平凡解(0 解),即系统的前7 阶非线性输出频率响应函数只有G1(j2πf),G3(j2πf),G5(j2πf) 和G7(j2πf) 为非0 解.
图3 表示用不同方法计算出的范德波尔系统前7 阶非线性输出频率响应函数,其中GALEs-RCM 曲线和GALEs-CCM 曲线分别表示用递归计算法和耦合计算法的计算结果.为了比较不同方法计算非线性输出频率响应函数的差异,这里与传统的最小二乘方法计算非线性输出频率响应函数作对比.由式(6)可知,非线性系统的输出响应频谱为

图3 范德波尔系统前7 阶非线性输出频率响应函数Fig.3 The first 7 nonlinear output frequency response functions of van der Pol system
最小二乘方法计算系统的前N阶非线性输出频率响应函数的表达式为[13]
其中,αm∈R+,表示系统输入激励的次数,N表示系统的截断阶数,.由式(33)可知范德波尔系统的前7 阶非线性输出响应只有y1(t),y3(t),y5(t) 和y7(t) 为非零解,取n={1,3,5,7},αm={0.7,1,1.3,1.5},,N=4 .图 3 中 的LSM 曲线为最小二乘法的计算结果.
图3 表明最小二乘方法可以准确地计算出低阶非线性输出频率响应函数,而广义伴随线性方程法可以准确地计算出任意高阶非线性输出频率响应函数,但递归计算法对高阶非线性输出频率响应函数的计算结果偏差较大,这是因为用Runge-Kutta 方法逐阶递归计算式(33)时,表1 中的第S2-1 步需要进行插值操作,目的是将离散化的yi(k) 进行连续化,便于求解高阶的广义伴随线性方程,但同时也引入了插值偏差,低阶广义伴随线性方程的数值计算偏差会随着低阶非线性输出响应一同作为高阶广义伴随线性方程的输入激励,从而使高阶广义伴随线性方程的数值计算偏差逐阶累积,最终导致高阶非线性输出响应计算结果偏差较大.由表2 中的第S2 步可知,耦合计算法在求广义伴随线性方程时并未进行函数插值操作,所以耦合计算法未引入插值误差,比递归计算法的计算精度更高,最终非线性输出频率响应函数的计算结果更准确.
图4 表示在耦合计算法中采用4 阶Runge-Kutta 方法(ODE45)的求解结果与递归计算法中采用8 阶Runge-Kutta 方法(ODE89)求解结果的对比,此时两种方法的最终计算结果基本一致.
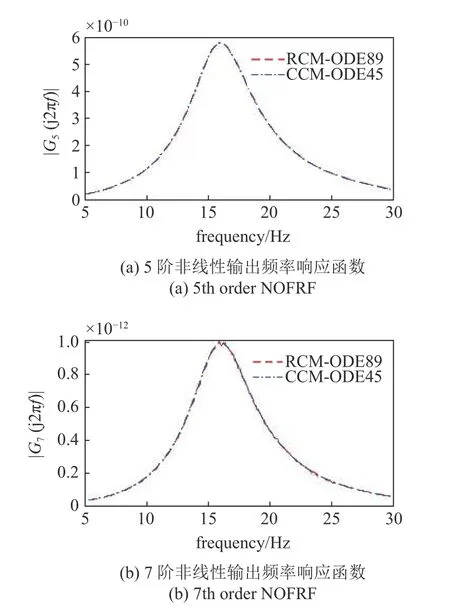
图4 耦合计算法与递归计算法对比Fig.4 Comparison of RCM and CCM
图5 表示在不同采样频率f s下分别由递归计算法和耦合计算法得到的范德波尔系统前7 阶非线性输出频率响应函数的计算结果,数值计算步长δt=1/f s.图5 表明由递归计算法计算出的高阶非线性输出频率响应函数的结果受数值计算的采样频率影响较大,而由耦合计算法计算出的高阶非线性输出频率响应函数的结果受采样频率影响较小.这是因为四阶Runge-Kutta 法(MATLAB,ODE45)是一种自适应步长的数值计算方法,所以耦合计算法求解过程中的计算步长会在多个方程中自适应调节,使得累计误差较小,最终计算结果受采样频率影响不大.递归计算法在求解广义伴随线性方程时,步长在各阶广义伴随线性方程中单独地自适应调节,所以计算高阶非线性输出频率响应函数时,递归计算法产生的累计误差较大,最终计算结果受采样频率影响较大.
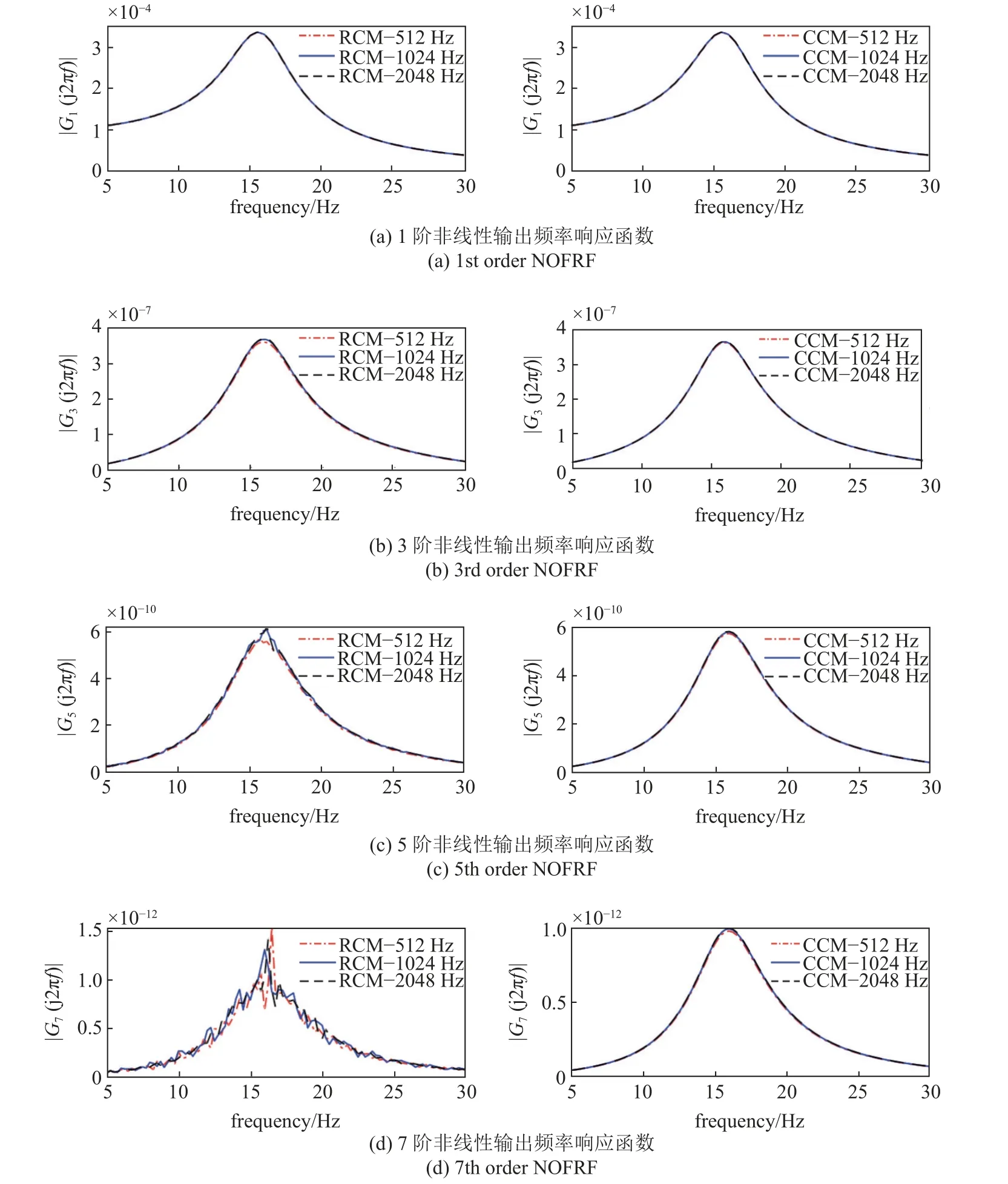
图5 RCM 和CCM 中采样频率对NOFRFs 的影响Fig.5 Effect of sampling frequency on NOFRFs in RCM and CCM
图6 表示在不同采样频率f s下,由递归计算法计算出的第i阶非线性输出频率响应函数的均方误差值(mean square error,MSE),其计算公式为
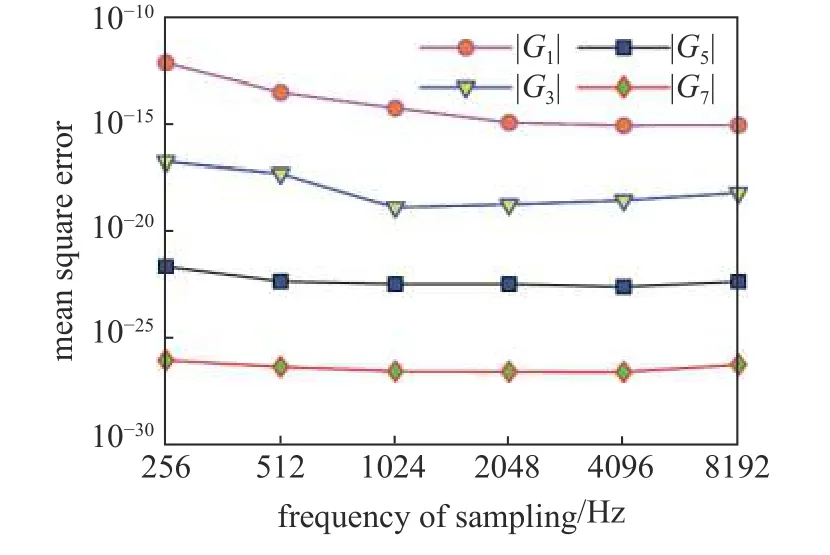
图6 采样频率对RCM 计算非线性输出频率响应函数均方误差的影响Fig.6 Effect of sampling frequency on the mean square error of NOFRFs calculated by RCM
图6 的计算结果表明:随着采样频率的增加,由递归计算法计算的高阶非线性输出频率响应函数的均方误差先减小后增大,这是因为初始采样频率增加时,计算步长减小,每步计算产生的误差减小,最终使计算结果的均方误差减小,但继续增加采样频率后,计算步数增加,计算结果的累计误差反而增大.所以递归计算法的累计误差不能直接通过减少数值计算的步长来降低,需要选择合适的采样频率才能达到较好的计算效果.
为了进一步比较递归计算法和耦合计算法的差异,需考虑噪声因素对两种计算方法计算结果的影响.在递归计算法和耦合计算法求解出的各阶非线性输出响应yi(t) 中加入一定量的白噪声,图7 表示在不同信噪比(signal noise ratio,SNR)的高斯白噪声影响下,递归计算法(RCM)和耦合计算法(CCM)的均方误差值变化曲线.噪声影响下递归计算法的均方误差值计算公式为
图7 表明在相同信噪比条件下,耦合计算法计算结果的均方误差值比递归计算法计算结果的均方误差值更小;同时,随着信噪比的增大,由递归计算法计算出的高阶非线性输出频率响应函数的均方根值不再递减,而耦合计算法计算出的高阶非线性输出频率响应函数的均方根值随着信噪比的增大仍在减小.所以相比递归计算法,耦合计算法在噪声影响下的计算误差更小.
此外,图8(a)和图8(b)分别表示用广义伴随线性方程的耦合计算法和最小二乘法计算出的范德波尔振子非线性参数CE对系统前7 阶非线性输出频率响应函数的影响,非线性参数CEi={0.5,1,1.5}CE.图8 的结果表明:
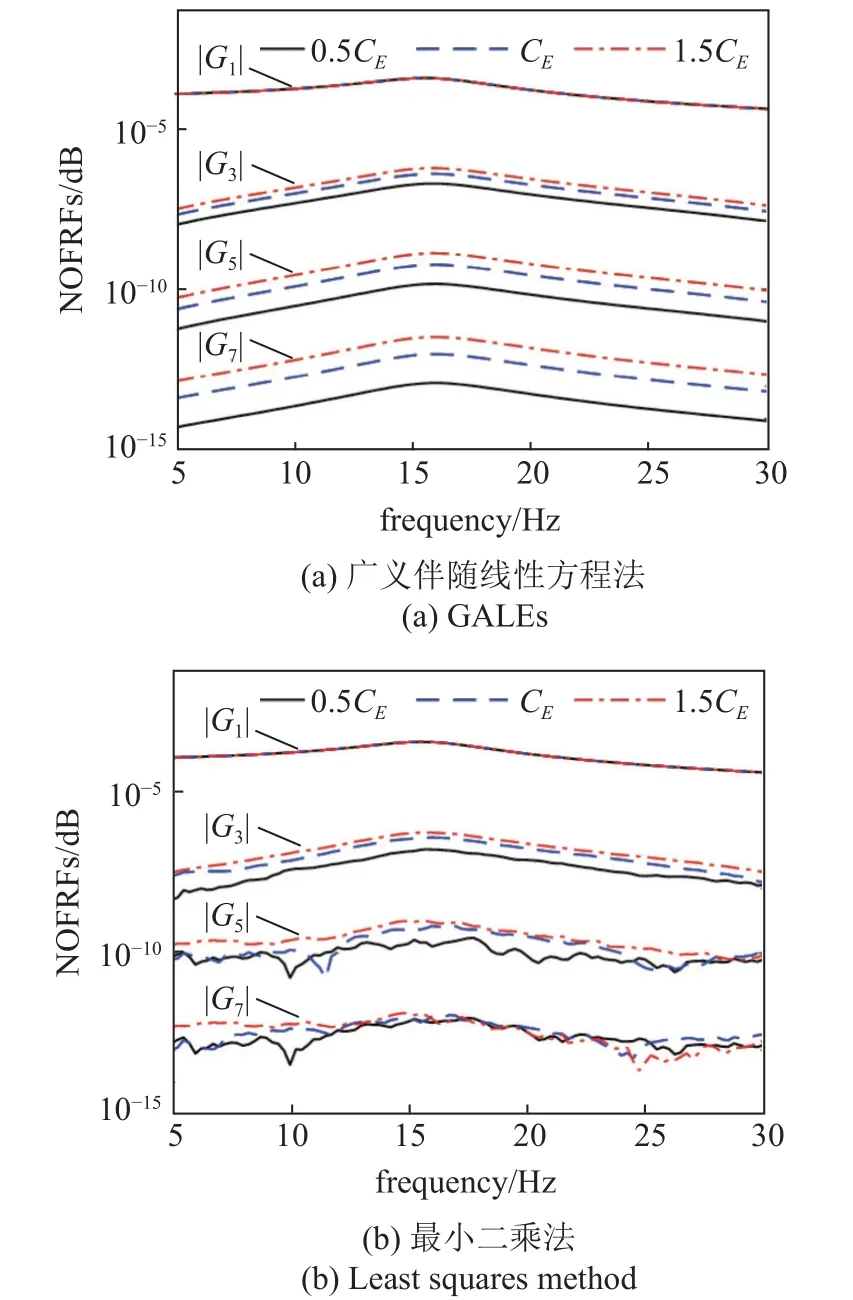
图8 非线性参数对NOFRFs 的影响Fig.8 Effect of nonlinear parameters on NOFRFs
(1) 非线性输出频率响应函数可以表示非线性系统的频域特征;
(2) 高阶的非线性输出频率响应函数可以表示系统非线性参数的变化;
(3) 高阶的非线性输出频率响应函数能量逐阶减小.
图8(a)表明,非线性参数对系统的1 阶非线性输出频率响应函数没有影响,这是因为1 阶的非线性输出频率响应函数本质上是非线性系统的线性派生系统频率响应函数,它不受系统非线性参数的影响.而非线性参数对其他高阶的非线性输出频率响应函数的影响较大,主要表现为非线性参数变化时,高阶非线性输出频率响应函数比低阶非线性输出频率响应函数变化明显,这表明高阶的非线性输出频率响应函数对非线性参数变化敏感程度更高,所以可利用高阶非线性输出频率响应函数对非线性参数变化的敏感性用于结构损伤检测及故障诊断.
图8(b)表明最小二乘法无法准确计算系统高阶的非线性输出频率响应函数.当非线性参数变化较小时,由最小二乘法计算出的非线性输出频率响应函数已无法表征系统的非线性参数变化,而广义伴随线性方程的耦合计算方法比最小二乘方法计算高阶非线性输出频率响应函数的误差小,最终计算结果更准确.
2.2 达芬(Duffing)系统
以带有立方刚度的非线性弹簧构成的达芬振子为例,系统的NDE 模型为
式中,m为振子质量,c为线性阻尼,k表示线性刚度,k3表示非线性刚度.
将式(44)代入式(26)中得系统的前五阶广义伴随线性方程为
许多工程系统可以看作是单输入单输出的非线性系统,其NDE 模型可用二阶微分方程表示为[25]
式中m,c,k,kj,j=2,3,···,J为系统参数,J为系统输出非线性项的最高阶数,将式(5)代入式(46)得
Feijoo 等[25]指出式(47)的伴随线性方程为
式中,j1+j2+···+jl=n.
将式(44) 代入式(48) 后可知达芬系统的前5 阶伴随线性方程与其广义伴随线性方程(45)的表达式完全一致,所以广义伴随线性方程法分析式(44)这类仅有输出整数次幂非线性项的系统时,它与伴随线性方程法的结果相同.同时,由伴随线性方程式(47)和式(48)可知,伴随线性方程法不能用于分析含有输入输出及其导数交叉项的非线性系统(例如范德波尔系统),所以广义伴随线性方程法比伴随线性方程法的适用范围更广.
在零初始条件下,式(44)所表示的达芬系统第2 阶与第4 阶非线性输出响应y2(t),y4(t) 均为零解,即y2(t)=y4(t) .式(45)为线性微分方程,因为谐波函数是微分算子的本征函数,所以对线性系统而言,输入激励频率与系统响应频率保持一致,如u(t)=cos(2πft),系统第1 阶非线性输出响应y1(t) 的频率成分与系统输入激励u(t) 的频率成分保持一致,即为f.第3 阶非线性输出y3(t) 的频率成分与系统3 阶广义输入激励-k3y13(t) 的频率成分相同,即为f,3f.同理,系统第5 阶非线性输出响应y5(t) 的频率成分与系统第5 阶的广义输入激励-3k3y12(t)y3(t) 的频率成分相同,即为f,3f,5f.由于达芬系统的偶数阶非线性输出响应y2k(t)=0,所以在谐波激励下的达芬系统只产生了奇数次谐波分量,这是因为达芬系统式(44) 的非线性项为y3(t),它仅包含输出y(t) 的3 次非线性项,即在式(26)中,只有输出非线性项系数Cp,0(l1,l2,···,lp)≠0,其余高阶广义伴随线性方程的非线性项系数均为0.由式(45)表示的达芬系统广义伴随线性方程也揭示了非线性系统在谐波激励时“倍数频率”现象产生的原因.
由式(45)得,非线性系统的广义伴随线性方程中线性算子 TL为
达芬系统的派生系统为
对单输入单输出的非线性系统,广义伴随线性方程的线性算子与非线性系统的派生系统表达式相同.派生系统的无阻尼固有频率.当系统(44)输入为谐波激励u(t)=cos(2πfnt/3) 或激励频率f=fn/r,r=3,5,7,··· 时,由式(45)可知,达芬系统第3 阶广义伴随线性方程的广义输入激励-k3y13(t) 中产生了与派生系统固有频率fn相同的谐波分量,此时系统第3 阶非线性输出响应y3(t) 出现了“次谐共振”现象.
表3 表示达芬系统前5 阶广义伴随线性方程的频率分布,其中f为单谐波激励的输入频率.
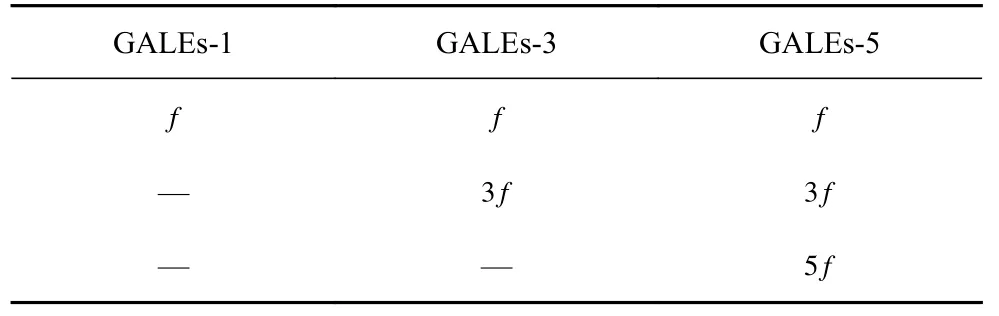
表3 广义伴随线性方程频率分布Table 3 Frequency distribution of GALEs
设达芬系统式(44) 的参数为:m=1 kg,c=30 N·s/m,k=1.0×104N/m,k3=5.0×108N/m3,输入u(t) 为
达芬振子线性派生系统的无阻尼固有频率为稳态响应由Runge-Kutta 方法计算得到.图9(a)~图9(c)表示由广义伴随线性方程计算的前5 阶非线性输出响应频谱,其中图9(a)表明第1 阶非线性输出响应y1(t) 的频率只有单倍频成分 5 Hz .图9(b)表明第3 阶非线性输出响应y3(t) 的频率包括单倍频成分 5 Hz 和3 倍频成分 15 Hz,图9(c)表明第5 阶非线性输出响应y5(t) 的频率包括单倍频成分5 Hz,3 倍频成分 15 Hz 以及5 倍频成分 25 Hz .由于谐波激励u(t) 的频率 5 Hz 接近达芬系统线性派生系统无阻尼固有频率 16 Hz 的1/3,所以系统的第3 阶与第5 阶非线性输出响应在 15 Hz 处出现共振.

图9 前5 阶非线性输出响应频谱Fig.9 Frequency spectrums of the first 5 orders of nonlinear output response
3 结论
本文基于NDE 模型表示的非线性系统广义频率响应函数递推公式及Volterra 级数理论,推导出了在一般激励下由NDE 模型表示的非线性系统广义伴随线性方程计算公式.该公式表明非线性系统的输出响应可以用一系列线性方程组的解来表示,该结果的正确性通过仿真实验研究进行了验证.针对NDE 模型的广义伴随线性方程的数值求解问题,提出了耦合计算和递归计算两种方法,研究结果表明,耦合计算法计算精度高,最终计算结果受数值计算采样频率的影响很小,能够准确地计算出系统非线性输出频率响应函数.此外,基于NDE 模型的广义伴随线性方程,研究了非线性参数对非线性输出频率响应函数的影响,为基于非线性输出频率响应函数在工程系统和结构的状态检测及故障诊断中的应用提供了一种新的思路.最后,以达芬振子系统为例,根据线性算子理论和广义伴随线性方程法分析了非线性系统中几种典型非线性现象产生的理论依据.本文研究表明,NDE 模型广义伴随线性方程法拓宽了伴随线性方程法的适用范围,对非线性系统的分析与设计具有重要意义.此外,由于NDE 模型广义伴随线性方程递归表达式计算复杂,不利于计算机编程实现及实际工程应用,如何改进其计算方法需进一步研究.

