空间机器人在轨组装多模块单元的对接力控制与地面实验1)

史玲玲 肖晓龙 张晓峰 范立佳 单明贺 ,2) 田 强

* (北京理工大学机械与车辆学院,北京 100081)

† (中国空间技术研究院遥感卫星总体部,北京 100094)

** (北京理工大学宇航学院,北京 100081)

引言

随着各航天大国太空战略部署及空间科学技术的发展,传统的航天器制造、部署和发射方式已不能满足现有太空探索的需求.受火箭推力、整流罩包络及机构复杂度的影响,当前的可展式结构难以满足未来深空探测、天文观测、战略侦察等工程所需的大面积、大跨度空间结构的构建要求[1-2],采用空间机器人在轨组装搭建为解决上述问题提供了新思路.

相比于有人在轨组装,自主在轨组装避开了人的介入,减少了运行成本,可应对复杂的大型空间结构的构建,是未来空间操作领域的主流方法[3-5].20 世纪90 年代,美国首先开始探索将自主在轨组装应用于太空任务的可行性[6].近年来,自主在轨构建技术在大型空间结构的搭建方面已经取得了显著进展,如美国主导的Archinaut 项目[7]、OSAM-1 项目[8]和詹姆斯·韦伯太空望远镜项目(JWST)[9],欧盟主导的MIRROR 项目[10],以及中国空间站项目[11].

空间机器人自主在轨组装主要通过以下3 种形式[12]:(1)固定基座的机械臂;(2)爬行机器人;(3)自由飞行机器人.固定基座的机械臂通常布置在大型航天器或空间站上,具有尺寸结构大、自由度多和承载能力强等特点;爬行机器人一般安装在导轨或大型桁架上,机器人一端在导轨上进行固定和移动,另一端用于执行在轨任务;自由飞行机器人摆脱了基座在航天器或导轨的束缚,能够执行更远范围的舱外任务[13-15].这3 种方案中自由飞行空间机器人拥有更好的灵活性和可达性,但存在基座与机械臂动力学耦合问题,其他问题如机械臂末端力控制则是3 种方式的共性问题.本文以自由飞行空间机器人为例,考虑了动力学耦合,同时研究了这3 种方案的共性问题,即组装过程的接触力控制.

空间机器人执行在轨组装任务时,末端执行器的运动及与目标物体接触碰撞产生的扰动力可能导致航天器部件摆动和位姿变化[16-17].杨胜丽等[18]针对机器人组装空间柔性结构的耦合动力学问题,提出了一种3 分支机器人的步态优化方法,从运动规划的角度有效抑制机器人组装过程中的结构振动.另一方面,为了减小在轨组装这种扰动力的影响,基于柔顺控制的在轨组装成为研究热点.Boning 等[19]提出采用太空机器人团队来操纵和组装大型柔性结构,并应用线性二次最优控制方法来确定定位结构所需的力,同时最小化组装过程的振动.樊茂等[20]分析了空间机器人抓捕目标过程中产生的碰撞冲击问题,提出了一种控制力矩能量消耗少且对卫星平台基座扰动小的镇定控制方法.Flores-Abad 等[21]提出了一种使用干扰观察器来获得精确的力估计的方法,其可作为阻抗控制器的反馈,进一步实现期望力的跟踪.陶东等[22]针对模型不确定的情况,提出了一种无力传感器的阻抗控制方法,实现了动力学模型不确定下接触力的估计补偿.朱安等[23]建立了双臂空间机器人捕获目标的闭链混合体系统动力学模型与二阶线性阻抗模型,实现了对接装置输出力的精确控制.Shi 等[24-25]针对在轨服务如在轨捕获、在轨维修中的力控制理论进行了研究,并通过仿真对力控方法进行了验证.综上,学者们在空间机器人在轨组装大型空间结构或在轨服务的动力学建模与控制方面取得了一定的成果,但针对空间结构多模块单元同步组装的复杂装配情形鲜有提及.此外,伴随空间结构的组装进程,空间机器人组装对接会受到空间结构大挠性、振动和太空环境的干扰,对接接触力控制难度大,现有方法少有考虑在轨组装过程中环境因素变化下的接触力控制.

另一方面,空间机器人的地面实验对于在轨组装中的理论研究、控制方法及控制策略的验证具有重要意义,其主要通过微重力环境模拟来演示空间机器人的工作场景.微重力环境模拟方法[26-28]主要有气悬浮法、水浮法、抛物线飞行法、自由落体运动法、吊丝配重法和机械臂硬件在环的半物理实验法.国内外各单位基于上述方法,开展了空间机器人原理样机验证及控制方法的研究.加拿大约克大学团队搭建了两套气浮式卫星模拟器的微重力试验台,设计实验验证了绳索张力控制、拖船姿态控制及其组合控制方法的有效性[29].欧洲航天局团队提出了一种V 形折叠杆式的锥形环状天线构造,研制了一套直径6 m 的可展开天线试验系统[30].我国南京航空航天大学团队基于空气轴承试验台,研究了追踪航天器模拟器与目标航天器模拟器的平面交会对接问题,并提出了多级控制策略,成功实现两者的无碰撞对接[31].哈尔滨工业大学周诚[32]为研究目标捕获任务下不同阶段的空间机器人控制问题,搭建了一套机械臂在环的地面实验系统,验证了相应的自主控制策略.

以上研究表明学者们在模拟微重力环境下空间机器人在轨组装技术的实验基础已较为扎实,但针对三维空间内模块组装的空间机器人运动控制,以及多接口对接力控制的地面实验研究尚有所欠缺.因此,本工作围绕空间机器人在轨组装大型结构多模块单元的情景,针对在轨组装复杂接触情形的建模与控制问题,开展多模块单元对接过程中柔顺对接的力控制方法和地面实验相关研究.其主要创新性在于:分析了在轨组装多模块单元(包括单-单接口、双-双接口、三-三接口)对接装配情景,将自适应阻抗控制方法应用于机器人组装多模块单元对接装配力的柔顺控制,并通过地面实验验证了该方法的可行性.本文的研究成果可为空间机器人在轨组装大型空间结构过程中的力控制提供理论基础和技术支撑.

本文内容的结构图如图1 所示.首先建立空间机器人在轨组装的动力学方程,针对空间大型结构模块组装情形,分析三维空间的接触动力学模型,为后续的实验验证奠定理论基础;其次考虑模块组装对接任务中对接力控制难及环境干扰强等特点,采用可用于多模块单元同时组装对接的自适应阻抗控制方法;最后建立空间机器人在轨组装仿真平台、飞行机器人地面实验平台和模块组装柔顺对接实验平台,以期对建立的运动学和动力学模型及所应用的自适应阻抗控制方法进行验证.

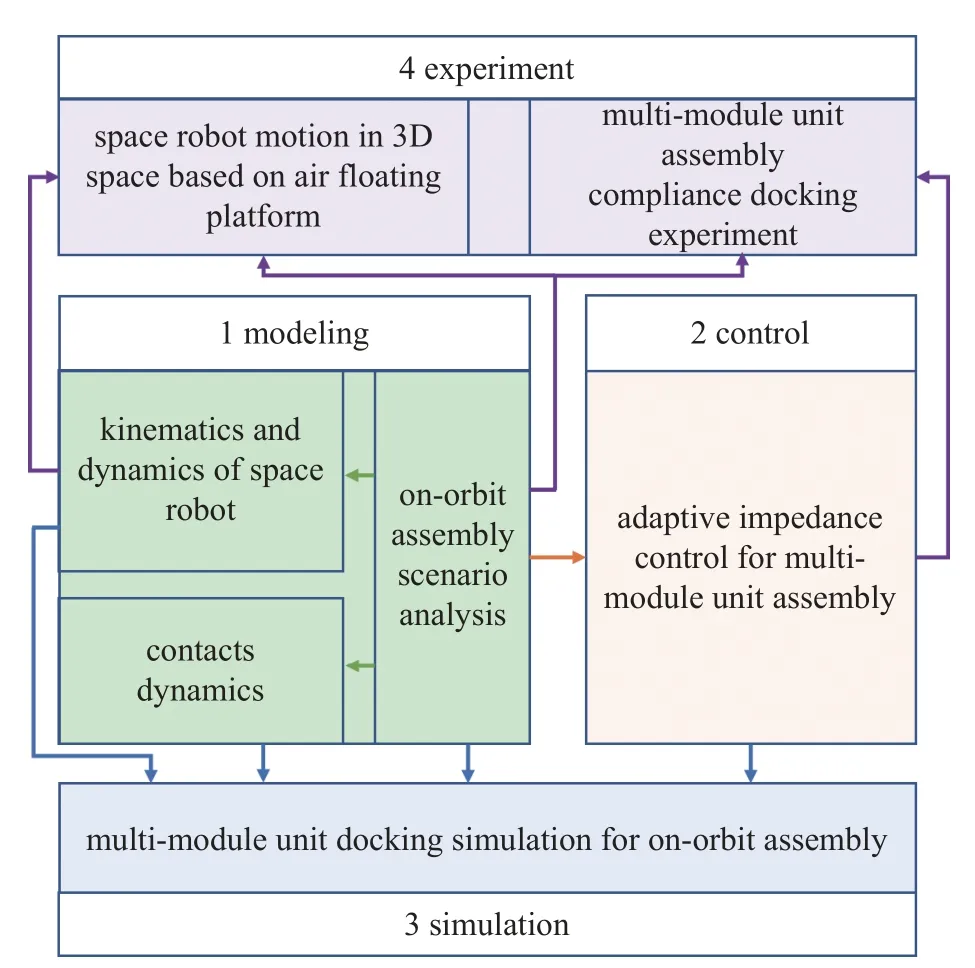
图1 文章结构图Fig.1 Structure of the paper

1 空间机器人在轨组装的动力学建模

1.1 多模块单元在轨组装情景分析

如图2 所示,空间机器人主要由可移动基座和多自由度机械臂组成,包含惯性坐标系 ΣI,固定在基座的坐标系 ΣB,原点位于空间机器人质心处的坐标系 ΣG,连杆坐标系 ΣLi以及目标坐标系 ΣT.其中空间机器人参数及其符号定义如表1 所示.在本文中,a{·} 表示在惯性坐标系中表示的变量.

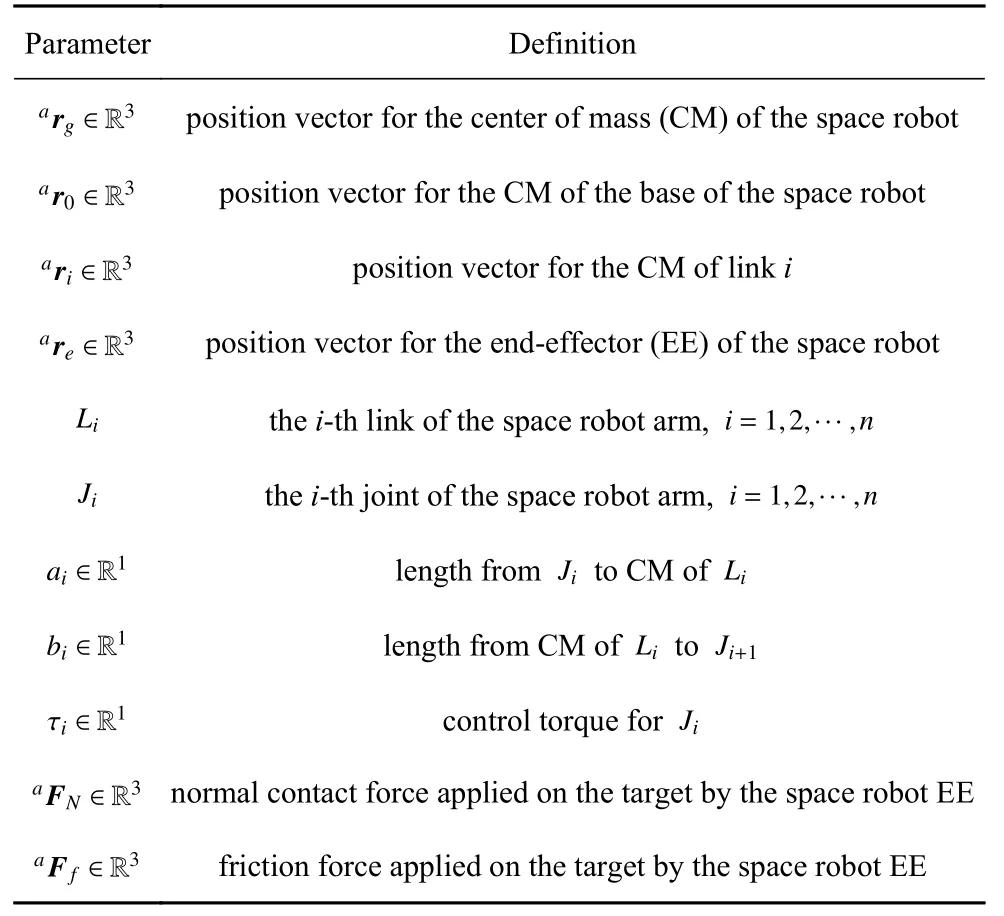
表1 空间机器人参数及含义Table 1 Parameters of the space robot

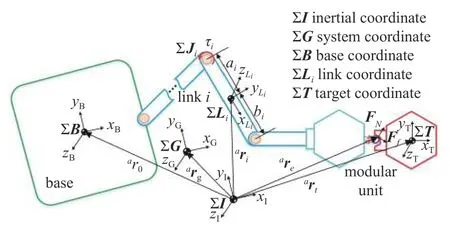
图2 空间机器人模型Fig.2 Space robot model

图2 所示为安装有n自由度操纵臂的单臂空间机器人和目标之间的对接场景,空间机器人末端执行器携带待组装模块单元与装配基体模块单元(目标)之间发生接触,并产生接触力.图3 展示的是空间大型结构模块单元组装时,不同数量接口接触的情景.在真实组装场景中,待组装模块相对固定块会存在偏心和偏转,因此机械臂在夹持待组装模块进行对接时,需根据力反馈信息来调整模块运动轨迹以实现柔顺对接.

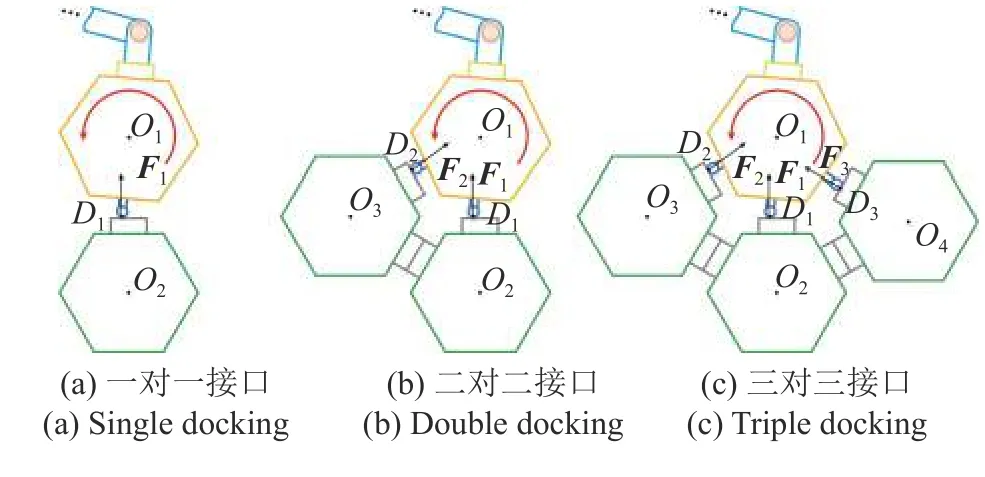
图3 空间大型结构模块单元组装情景Fig.3 Docking scenarios for different quantities of modular units

由于系统的浮动特性,空间机器人的基座位姿会受到机械臂运动以及接触力/力矩的干扰.因此,在图2 的定义中,需确定惯性坐标系、空间机器人坐标系和目标坐标系之间的转换关系.另外,针对空间机器人在轨组装场景,本文有如下假设:

(1) 组装操作是在近距离进行的,因此不考虑轨道动力学;

(2) 单臂空间机器人包含可控基座和n自由度连杆,所组装模块聚焦于小型模块,故空间机器人系统和空间结构模块单元均设为刚性体,结构柔性暂不考虑;

(3) 整个控制过程分为两个阶段,即接近阶段和接触阶段,目标始终处于空间机器人的工作空间内;

(4) 目标的参数和运动可以被测量或估计.

1.2 空间机器人的运动学和动力学建模

由于空间机器人末端执行器需要以特定姿态对目标施加所需的力,因此建立空间机器人末端位姿与关节运动和基座姿态的速度级关系为

式中,ve和 ωe分别代表机械臂末端执行器的线速度和角速度,vg和 ωg分别代表空间机器人系统质心的线速度和角速度;J∈R6×(n+3)表示空间机器人的广义雅可比矩阵,,其中 ΦS=[α,β,γ]T表示空间机器人基座的姿态角,表示机械臂的关节角度.

空间机器人在执行在轨组装任务过程中,其末端携带待组装模块单元与已组装装配基体发生物理接触,从而受到外力作用.本文采用牛顿-欧拉方法构建空间机器人的动力学方程得

式中A∈R(n+3)×(n+3)代表空间机器人的惯量矩阵,B∈R(n+3)×1表示非线性项,JF∈R(n+3)×6表示雅可比矩阵转置,其中 τS表示空间机器人基座的姿态控制力矩,τM表示机械臂的关节力矩.

1.3 三维空间接触动力学建模

模块单元对接时,由于其对接机构相对空间机器人在轨组装系统整体小得多,因此模块单元两两对接的接触被简化为球锥点接触[33].机器人所携带组装单元对接杆前端的球头与装配基体模块单元的对接锥发生相互接触并最终通过机构锁紧建立连接,如图4 所示.

图4 两模块单元对接简化示意图Fig.4 Simplified docking process of module assembly

在组装对接过程中,基于机器人的运动控制,碰撞接触只发生在主动对接模块的球头和被动对接模块的接纳锥内壁上,主动模块的对接杆始终不与对接锥的内壁接触.由于球头和接纳锥均为回转体,因此当球头与接纳锥内壁发生碰撞时,碰撞点即为球面上的点与锥内壁面上的点的重合处,其可由一个过球心和回转轴线的截平面来体现.此时,接触球头与对接锥在空间的三维接触问题被转化为二维平面来进行求解,如图5 所示.

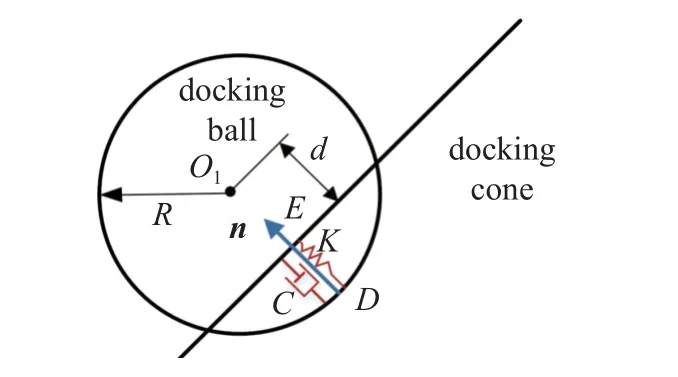
图5 Hunt-Crossley 接触碰撞模型Fig.5 Hunt-Crossley contact model

对接球头和对接锥碰撞时发生相互渗透嵌入,设接触点为D,球头半径为R.球头与对接锥的内壁碰撞时两者之间的法向侵入深度为

式中d表示对接球头球心到直线AB的距离.

根据Hunt-Crossley 接触模型,对接球头与对接锥面之间的法向接触力FN可表示为

式中,Fk为接触过程中的弹簧恢复力,K为球头与对接锥之间的接触刚度,p为力指数;Fd为接触过程中的阻尼力,C为阻尼系数,为对接球头和对接锥在接触点处的法向相对速度.

如图6 所示,由于接触球头和对接锥在接触点处存在相对运动,球头和对接锥之间会产生摩擦力,采用Coulomb 摩擦力模型进行切向碰撞力的计算,得

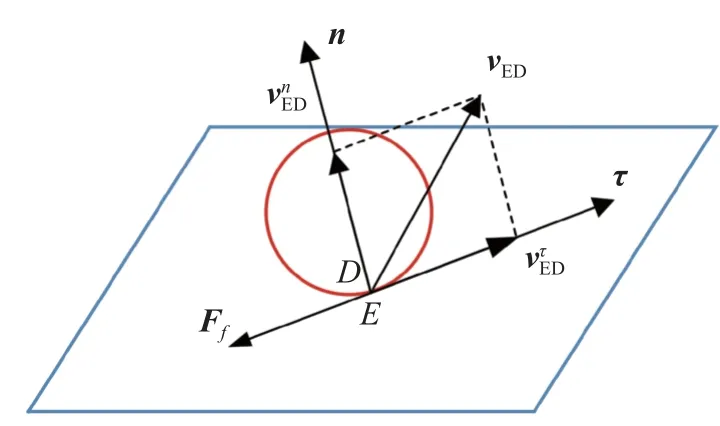
图6 摩擦力模型Fig.6 Friction model

其中摩擦力Ff的方向与vED在切平面上的投影反向共线.

2 面向多模块单元组装的自适应阻抗控制方法

在轨组装过程中,装配基体呈现变拓扑变刚度的特性,同时机器人的运动可能会导致大型结构发生振动.此外,太空环境中存在外界干扰力/力矩.这些因素使得对接过程复杂且存在一定的不确定性,必须对对接过程的接触力进行控制,避免接触力过大对结构造成破坏.针对上述情况,在基于位置的阻抗控制基础上,采用了文献[34]提出的模型参考自适应阻抗控制策略(model reference adaptive impedance control,MRAIC),从而提高控制系统对环境变化的适应能力,通过实时调整控制参数来调整顺应轨迹,最终实现力的稳定跟踪,具体控制框图如图7 所示.

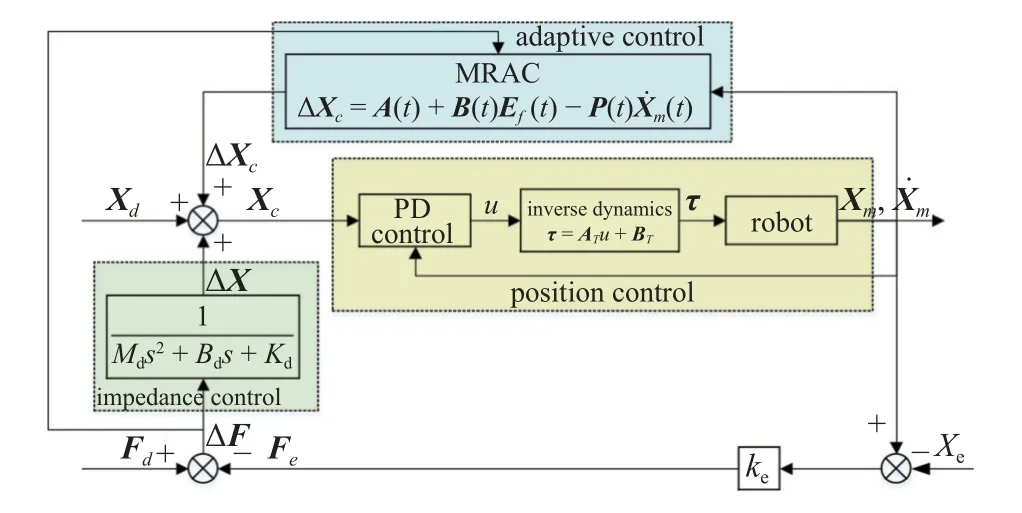
图7 模型参考自适应阻抗控制Fig.7 Model reference adaptive impedance control (MRAIC)

定义Xm为机器人末端的实际位置向量,Xd为机器人末端的期望位置向量,Xe为环境位置,Xc为阻抗控制顺应轨迹.令末端位置偏差 ∆X=Xm-Xd,故机器人末端位置偏差和环境之间的阻抗方程为

式中Md,Bd,Kd∈R6×6分别代表目标阻抗模型的惯性矩阵、阻尼矩阵和刚度矩阵;Fe代表机械臂末端与环境的接触力,Fd代表期望力,Ef代表力误差.

本文使用的间接调整律在原调整量的基础上增加了一调整信号 ∆Xc,通过自适应律推导出新的实时目标阻抗关系.以单自由度情形为例进行分析,在期望轨迹中增加误差项 ∆xc,则此时的期望轨迹为

在模块单元对接球头和对接锥发生接触碰撞时,由于引入了调整信号 ∆xc,机器人末端位姿会根据力反馈信息实时调整,使对接力不超过允许阈值,并在达到稳态时跟踪期望力.令 ∆xc为[35]

式中,ef(t) 代表力跟踪误差;a(t),b(t) 和p(t) 均为时变系数.

由于位置伺服控制具有较高精度,跟踪轨迹误差相较于末端位置偏差小1～2 个数量级,因此可以认为xc≈xm.将机器人末端与环境接触模型简化为线性弹簧系统,故力跟踪误差为

在模块单元对接任务中,对接球头和对接锥的接触过程具有低阻尼和低惯性的特性,故,.另外,当系统输入的期望力fd为恒值时,有.对式(9)进行一次和二次求导,并代入到阻抗方程式(6),可得

由于期望轨迹经自适应律增加了一个调整项∆xc,故用替换式(10)中的xd,并代入式(8)到式(10),化简并整理可得

设计一理想二阶参考模型

设式(8)中时变参数的控制律为[33]

式中,c0,c1,µ1,µ2和 µ3均为较小的正常数;a0,b0,p0为对应时变系数的初值;σ1,σ2和 σ3均 为正的修正常数.

对式(17)进行求导并联立式(12)得

其中 α1,α2和 α3均为正常数.

定理1在式(17)所示控制律的作用下,式(16)所示系统方程在平衡状态处渐近稳定.

证明令李雅普诺夫函数V(Ee,t) 为[34]

其中P为非奇异对称正定矩阵.则当Ee和t不为0 时,函数V为正值,即V正定.

对函数V求导并联立式(18)可得

其中Q为正定对称矩阵.

由于阻抗控制方程在各维方向上近似解耦,为解决空间机器人在完成空间大型结构组装时的接触问题,将式(21)扩展为空间三维形式得

式中B(t),P(t)∈R6×6;∆Xc(t),A(t)∈R6×1.

3 仿真与实验

本节首先通过半物理仿真模型验证空间机器人动力学模型和力控算法的准确性,然后搭建了基于气浮法的飞行机器人实验平台,设计了飞行机器人运动实验,以探究动力学耦合效应和运动学理论模型的正确性,最后通过模块单元组装对接实验平台进行不同数量接口的对接实验,从而验证模型参考自适应阻抗控制方法的有效性.

3.1 组装对接仿真

为了验证空间机器人在轨组装的控制方法,搭建了半物理仿真平台.空间机器人的完整CAD 组件和结构模块单元模型分别导入到仿真软件中,其中模型的质量、惯量、几何参数等与理论模型保持一致.下面首先介绍模块单元组装全过程的控制策略,然后分别通过一对一和三对三接口的对接情景仿真,验证模型参考自适应阻抗控制方法的可行性.

3.1.1 控制策略

三维空间的组装任务中,飞行机器人使用末端执行器夹持待组装模块单元经空间运动接近已组装模块基体.到达指定预组装对接位置后,通过机器人末端的运动带动待组装模块与固定组装模块单元进行对接,对接全过程流程如图8 所示.

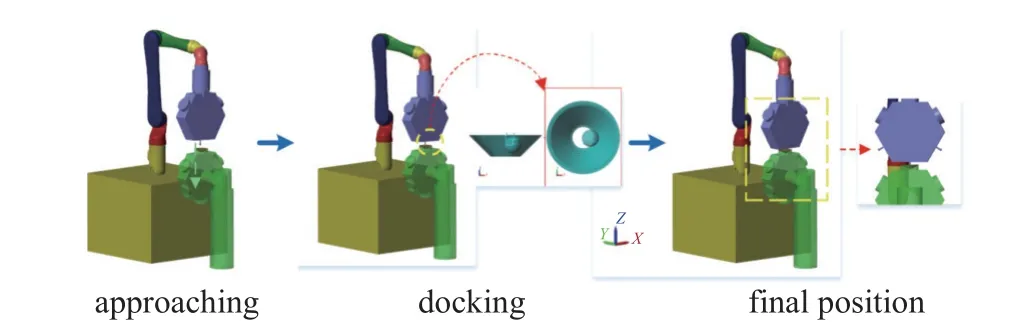
图8 模块对接流程Fig.8 The process of module docking

空间机器人完成大型空间结构模块单元组装的接近阶段和对接接触阶段的控制策略如下.

(1)接近阶段

空间机器人末端执行器携带待组装模块接近装配基体模块单元的期望轨迹可用5 次多项式表示为

其中,X(t0) 表示末端执行器的初始状态,代表预组装对接位置.tnx=t/tfx,其中t和tfx分别表示当前时间和到达预组装对接位置所需的总时间.

基于传统的计算力矩法,接近阶段的控制律为

(2)接触阶段

当飞行机器人末端所携带的待组装模块与已组装基体模块开始对接,模块单元上的对接杆和另一个模块的对接锥发生接触碰撞,接触过程期望接触力设为Fd1=[0,0,-2,0,0,0]T,其中前3 项为三维接触力,单位为 N,后3 项表示为接触过程产生的力矩,单位为 N ·m .对接过程中,同样给出飞行机器人末端从预组装位置运动到对接完成理想位置的期望轨迹为

结合上述对接触力实施控制的自适应阻抗控制策略,接触阶段的控制律为

当对接杆落到对接锥孔底部时,认为对接任务完成,此时设置期望接触力Fd2=[0,0,0,0,0,0]T.

综上,模块单元对接全过程的控制流程如表2所示.

表2 模块单元对接的控制流程Table 2 Control of the space robot during module docking

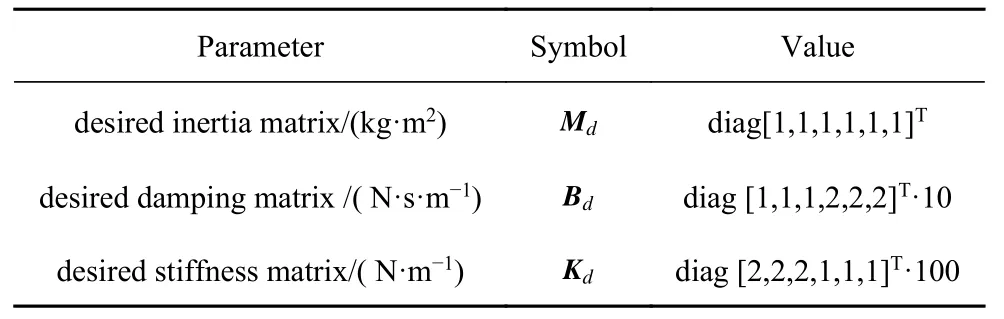
表3 阻抗控制器参数Table 3 Parameters of impedance controller

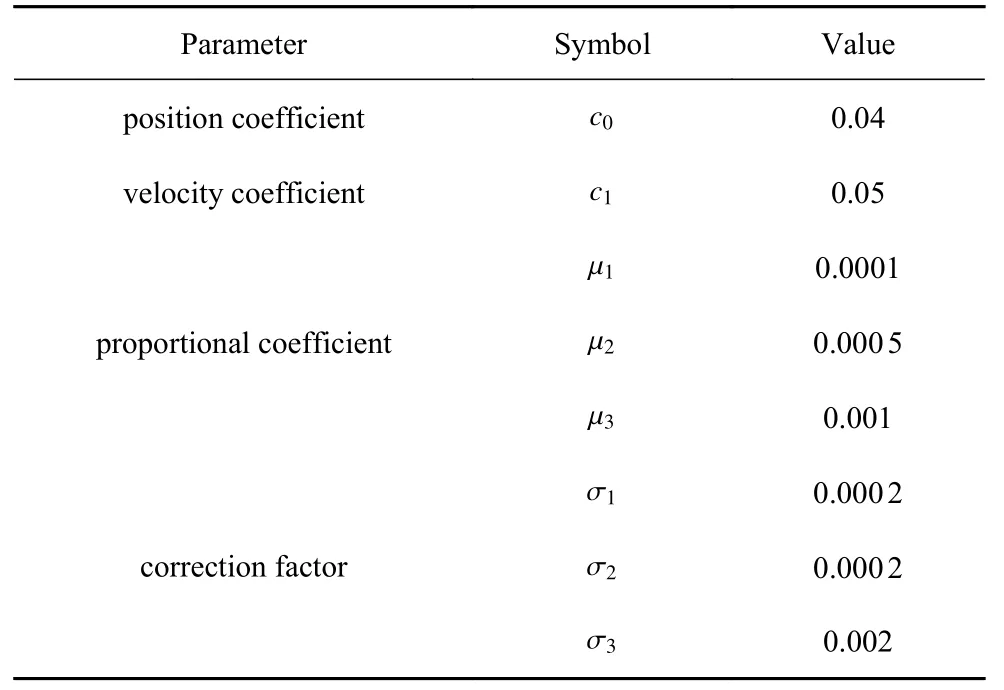
表4 自适应控制器参数Table 4 Parameters of adaptive controller

3.1.2 仿真实验

考虑到机械臂本身的运动控制精度,以及已组装模块由于空间结构大挠性引起的位置变化,设置待组装模块相对装配基体模块在接触阶段存在对接初始偏差:δ为在已组装模块x轴负方向5 mm、θ为绕y轴旋转2°,组装对接方向沿惯性坐标系z轴,如图9 所示.

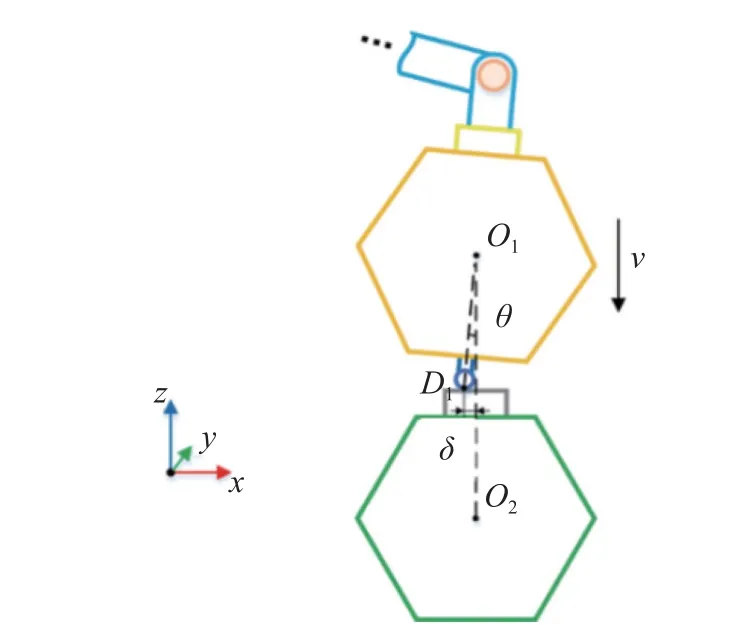
图9 仿真初始设置Fig.9 Simulation initial settings

模块单元单接口对接和三接口同步对接的情景分别如图10 和图11 所示.

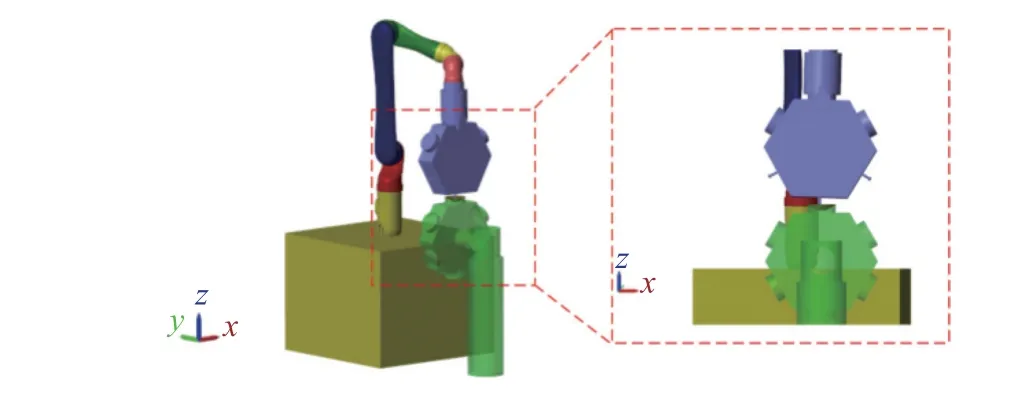
图10 一对一接口对接情景Fig.10 Docking scenario of single interface

图11 三对三接口对接情景Fig.11 Docking scenario of three interfaces

在一对一对接情景下,采用模型参考自适应阻抗控制,其末端力输出曲线和位姿误差分别如图12和图13 所示.

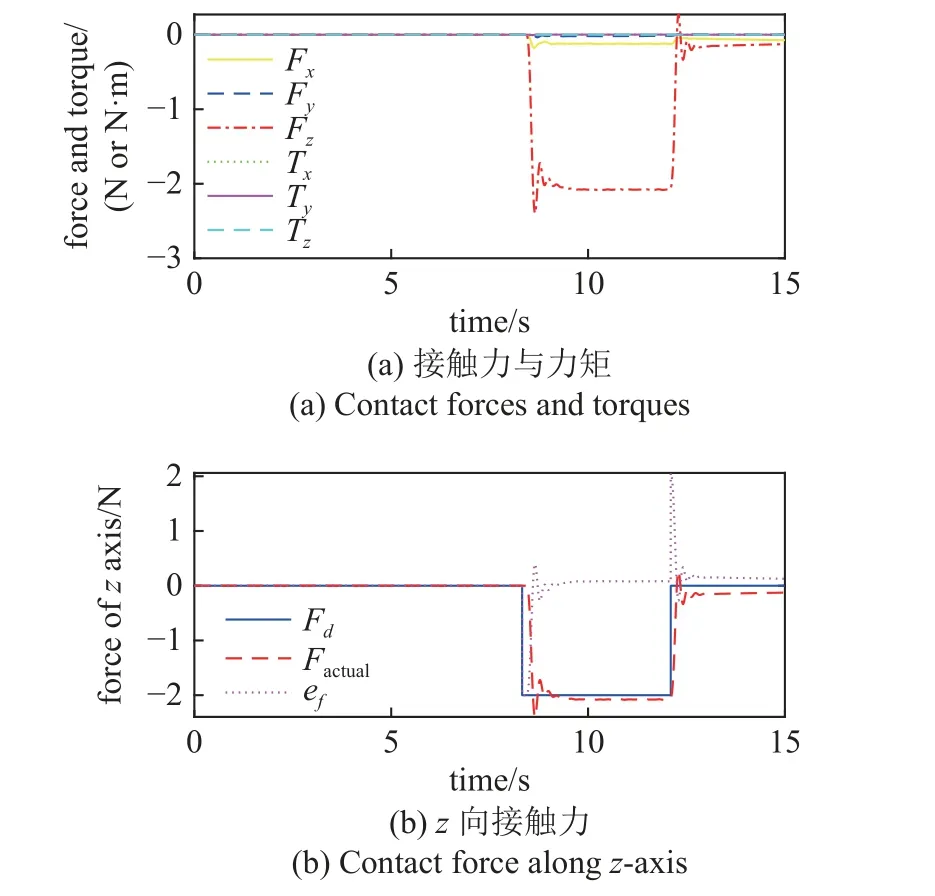
图12 自适应阻抗控制下一对一接口末端接触力Fig.12 EE contact force of single interface docking under adaptive impedance control

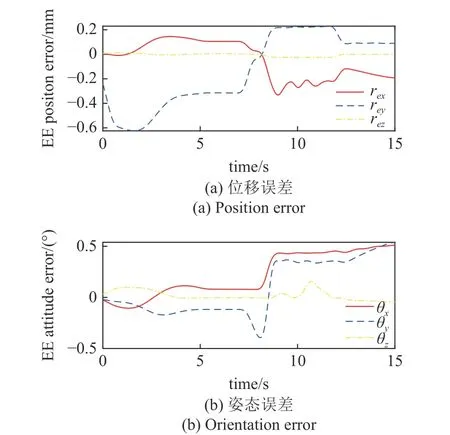
图13 自适应阻抗控制下一对一接口的位姿误差Fig.13 EE pose error of single interface under adaptive impedance control

图12(a)所示为模型参考自适应阻抗控制的末端六维力/力矩输出曲线.从图中可以看出,在8.3 s发生对接碰撞,接触力有一段爬升过程,其中z轴方向接触力最大峰值为2.45 N,在12 s 到达对接位置完成对接后,接触力能快速降低并达到稳态.图12(b)表示自适应阻抗控制方法在z轴方向的力跟踪误差输出曲线,可以看到在接触阶段,模型参考自适应阻抗控制方法的稳态力误差在0.1 N 以内,对接完成后,接触力也能快速收敛到期望值0 N 附近.从图13(a)和图13(b)可以看出,自适应阻抗控制方法下的位姿跟踪误差均在1 mm 和1°以内,满足对接任务的末端位姿精度要求.

同样在三对三对接情景下,采用模型参考自适应阻抗控制,其末端力输出曲线和位姿误差分别如图14 和图15 所示.

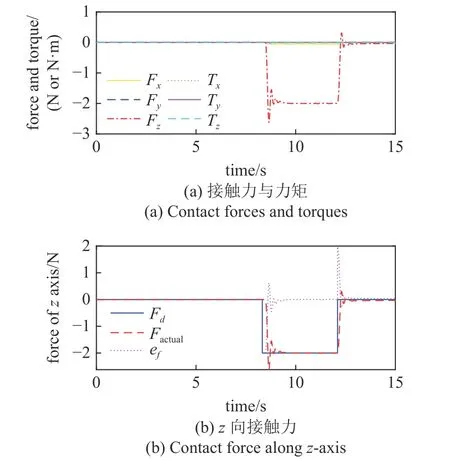
图14 自适应阻抗控制下三对三接口末端接触力Fig.14 EE contact force of three interfaces under adaptive impedance control

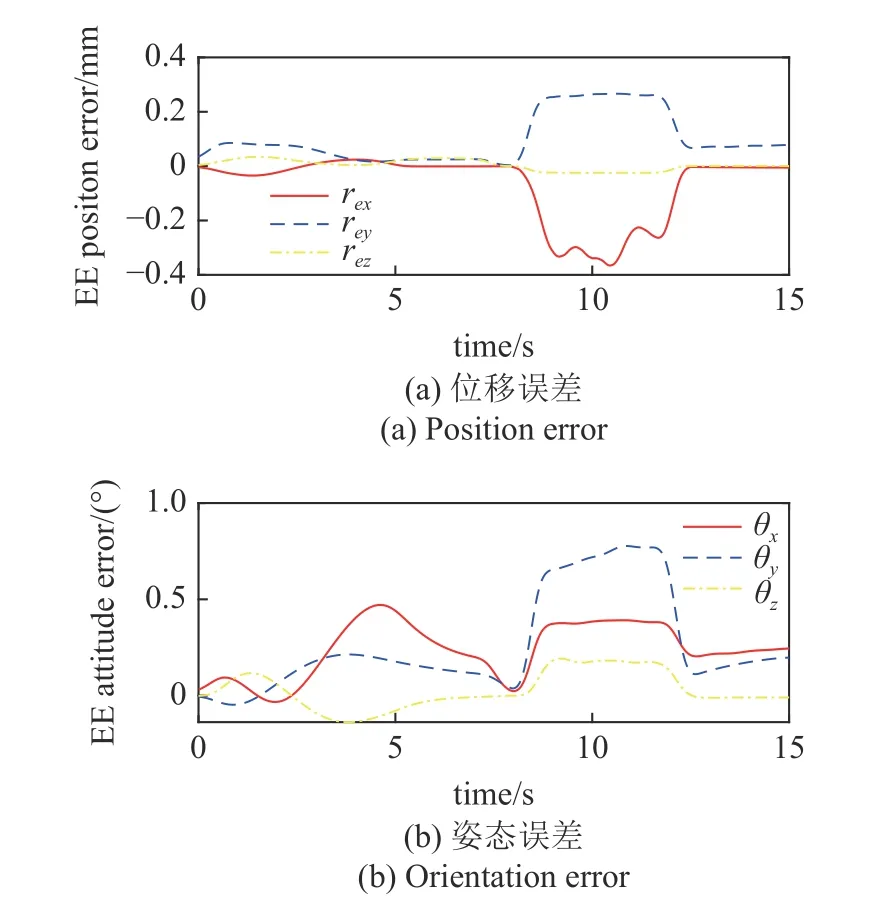
图15 自适应阻抗控制下三对三接口位姿误差Fig.15 EE contact pose error of three interfaces adaptive impedance control

图14(a)表示模型参考自适应阻抗控制的末端力输出曲线,从图中可看出在8.3 s 发生对接碰撞瞬间,接触力有一段爬升过程,其中z轴方向接触力最大峰值为2.6 N,在12 s 到达对接位置完成对接后,接触力均能快速降低并达到稳态.图14(b)表示自适应阻抗控制方法在z轴方向的力跟踪误差输出曲线,可以看到在接触阶段,模型参考自适应阻抗控制方法的稳态力误差在0.1 N 以内,在对接完成后,自适应方法下接触力也能快速收敛到期望值0 N 附近.从图15(a)和图15(b)可以看出,对于三对三模块对接情形,自适应阻抗控制方法下的位姿跟踪误差均在1 mm 和1°以内,满足对接任务的末端位姿精度要求.

从模块单元一对一对接到三对三对接,不同数量接口对接会使环境模型刚度发生变化,而自适应阻抗控制方法仍能保证良好的力跟踪性能.在三对三接口的多点复杂接触情景下,自适应阻抗控制策略下的系统控制精度较高,响应迅速,达到稳态时间短,满足对接任务需求.

3.2 三维空间中空间机器人运动实验

3.2.1 实验平台

为模拟三维空间中的对接组装任务,搭建了如图16 所示的气浮飞行机器人模块组装物理实验系统.该系统主要包括大理石平台,气浮轴承支撑的多自由度飞行机器人仿真器,由该飞行机器人机械臂抓取、运送和对接的结构模块,以及支撑桁架、测量和通讯设备.飞行机器人的系统硬件如图17 所示,包括Kinova 机械臂、工作站PC、惯性测量单元IMU、交流电池、高压气瓶和气浮轴承.系统软件集成环境为Ubuntu 18.04 操作系统和ROS Melodic框架,控制程序主体使用C++语言.

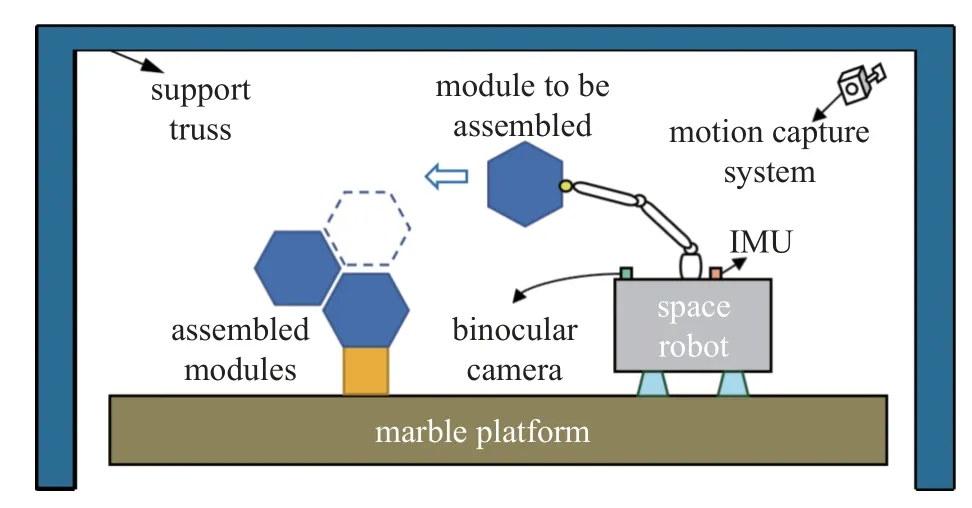
图16 模块组装物理实验系统Fig.16 Experimental system of modular assembly

图17 飞行机器人系统平台Fig.17 Flying robot system platform

3.2.2 耦合运动

为验证飞行机器人的动力学耦合效应,在气浮条件下,控制机械臂运动,观察基座运动状态.具体实验方案为:将机械臂调整到某一固定构型,然后给予机械臂第一关节(底部根关节)以固定角速度关节输入,利用IMU 测量基座在大理石平台上绕自身z轴的旋转角速度,实验过程如图18 所示,其中 Σa为系统的惯性坐标系.

图18 飞行机器人耦合运动实验Fig.18 Coupled motion of flying robot

从图18 可以看出,当机械臂绕za轴顺时针方向旋转时,基座在耦合效应下沿逆时针方向旋转,该运动状态符合耦合运动的理论公式

式中,Ibz和Imz分别代表基座和机械臂对于z轴的转动惯量,ωbz和 ωmz分别代表基座和机械臂沿z轴的旋转角速度.Ibz根据机器人构型采用CAD 模型计算得出,在关节角q=[0,225◦,135◦,240◦,83◦,75◦]T的构型下,机械臂的转动惯量为0.5954 k g·m2.Imz利用转动惯量实验仪测量而得,结合平行轴定理,最终测算基座的转动惯量为2.053 k g·m2.

设定不同的角速度值作为机械臂第一关节的输入,多次实验采集基座运动数据,同时通过式(27)计算各组机械臂运动对应的基座运动理论值,结果如表5 所示,绘制基座运动实际数据和理论值对比图,如图19 所示.

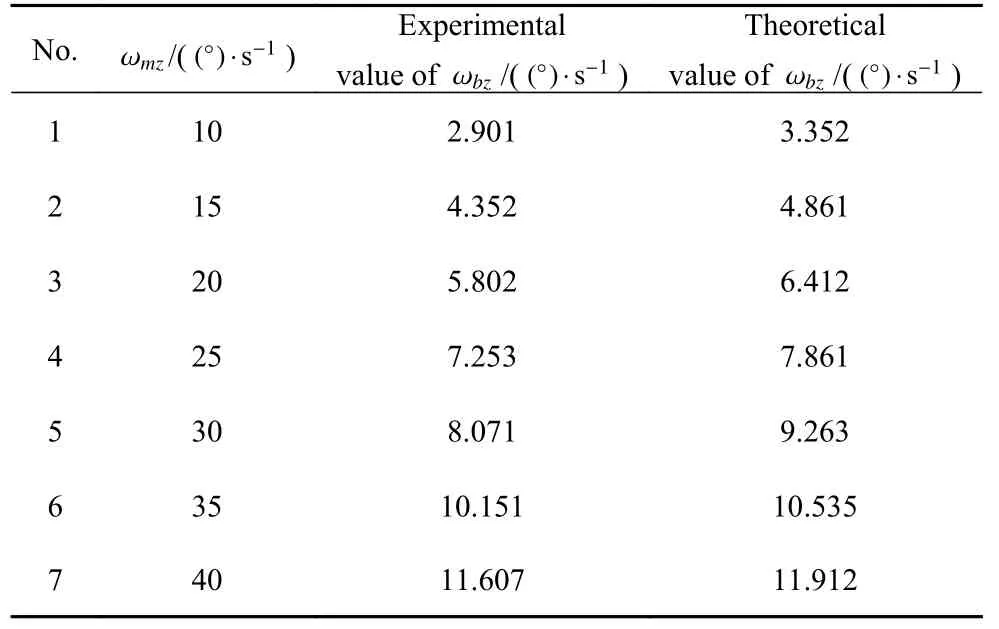
表5 基座运动实际数据和理论值Table 5 Experimental and theoretical values of base motion

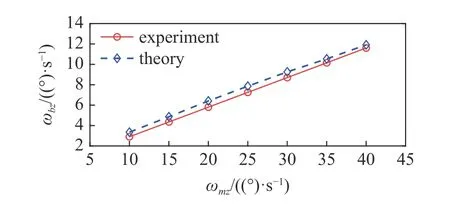
图19 基座运动实际数据和理论数据对比图Fig.19 Comparison of actual and theoretical base motion

表5 和图19 反映出基座的实际运动数据均小于理论计算数据,这是由机器人与气浮平台间仍存在一定阻尼导致,也就是理论公式(27)中应附加一个阻尼项,即

因此,尽管实验数据与理论值存在一定的偏差,但从实验数据拟合曲线来看,实验值和理论值均呈现良好的线性关系,从而验证了地面飞行机器人实验平台空间运动的动力学耦合现象.需要说明的是,由于重力和支持力的作用,飞行机器人系统在x轴和y轴方向的角动量并不守恒,因此该文只设计了z轴转向的耦合运动验证实验.

3.2.3 运动学模型验证

为验证飞行机器人运动学模型(式(1))的正确性,在气浮条件下,控制机械臂末端在笛卡尔空间进行运动,观察基座在机械臂反作用力(矩)下的运动状态.具体实验方案为:(1)打开动捕系统,采集全过程运动数据;(2) 气浮平台自由漂浮一段时间(约10 s);(3)启动实验控制指令;(4)记录关节运动数据.实验控制框图如图20 所示.

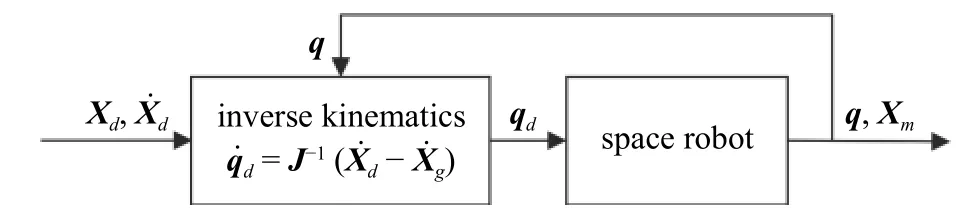
图20 运动学验证实验控制框图Fig.20 Experimental scheme for kinematics verification

由于大理石平台存在一定的倾斜角度和摩擦阻尼,飞行机器人运动过程中会受到平台带来的干扰,基于飞行机器人自由漂浮阶段的运动数据以拟合干扰曲线.全过程运动数据排除干扰曲线后即可获得该次实验进行平台干扰补偿后的基座运动曲线.

机械臂的笛卡尔空间运动分别设定为:(1)沿惯性坐标系z轴方向运动 +0.2 m;(2)沿惯性坐标系x,y和z轴方向分别运动 +0.2 m,-0.2 m 和0.2 m;(3)沿惯性坐标系x,y和z轴方向分别运动-0.2 m,-0.2 m 和 +0.2 m.每组分别进行多次实验,通过光学三维动作捕捉系统和IMU 分别对基座的位置和姿态进行测量,并将补偿后的基座运动数据与理论模型的运动数据作对比,得到运动过程末端执行器的最大跟踪误差值,如表6 所示,其中某次实验的运动数据(去除自由漂浮时段)如图21 所示.

表6 机械臂末端运动最大跟踪误差值Table 6 Maximum tracking error during EE motion

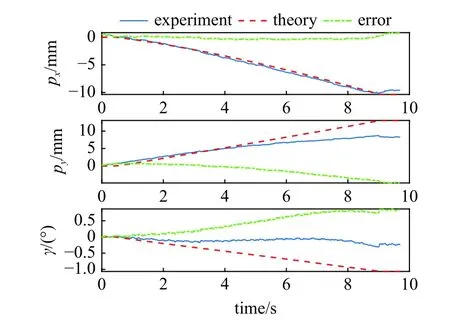
图21 补偿后与理论基座运动数据Fig.21 Compensated and theoretical base motion data

从表6 和图21 可以看出,补偿后的基座运动数据与理论模型的运动数据变化趋势一致,但数据之间仍存在一定的偏差,最大跟踪误差在6 mm 和1°以内.这是由于飞行机器人在空间运动过程中的机械臂构型发生变化,机械臂的质量分布变化,因此各气浮轴承上的压力也会随之变化,导致气膜厚度改变,从而使气浮轴承与平台的摩擦力发生改变.由于气浮平台的气浮效果发生改变,其所受平台摩擦干扰不同,因此拟合出的干扰二次曲线与真实值之间存在一定的误差,但从基座补偿后和理论值运动数据的变化趋势来看,在5 s 以内,两者的运动曲线十分接近,误差在1 mm 和0.5°以内,从而证明了飞行机器人运动学模型的正确性.为了避免平台干扰造成飞行机器人末端运动精度低的问题,可通过笛卡尔空间的闭环运动控制来提高运动控制精度,其控制框图如图22 所示.

3.3 多模块组装的柔顺对接实验

目前实际的空间大型结构在轨组装应用情景中,多采用固定基座的机械臂来执行任务,如中国空间站上搭载的大型固定基座机械臂.对于利用漂浮的空间机器人执行模块组装任务,其基座的位姿往往是受控的.本节主要针对模块单元组装中的多接口复杂对接接触情景,设计了模块单元组装的柔顺对接实验平台,将机器人固定在光学平台上对模块单元实施组装,用以模拟固定在大型结构基体的空间机械臂或自由飞行空间机器人基座受控的工况.

3.3.1 实验平台

模块单元组装的柔顺对接实验平台如图23 所示,包含机械臂、待组装模块单元、对接机构以及支撑结构.其中机械臂使用的是Franka Emika 7 轴机械臂,其负载为3 kg,工作半径为855 mm,重复定位精度为 ± 0.1 mm,控制频率1000 Hz.机器人7 个关节分别内置扭矩传感器,因此能够通过读取扭矩传感器数据从而对外力进行估计,末端力分辨率0.05 N,力矩分辨率0.02 N·m.

图23 模块单元对接实验系统Fig.23 Module unit docking experimental system

模块单元及对接接口尺寸信息如图24 所示,其中对接模块为正六棱柱,宽10 mm,其正面投影为内接圆直径为150 mm 的正六边形;对接杆长为89 mm,端部带有半径为10 mm 的半球;接纳锥锥角为120°,最小圆锥直径为11 mm,圆锥长度为24 mm.实验平台关于XZ和YZ平面对称布置.

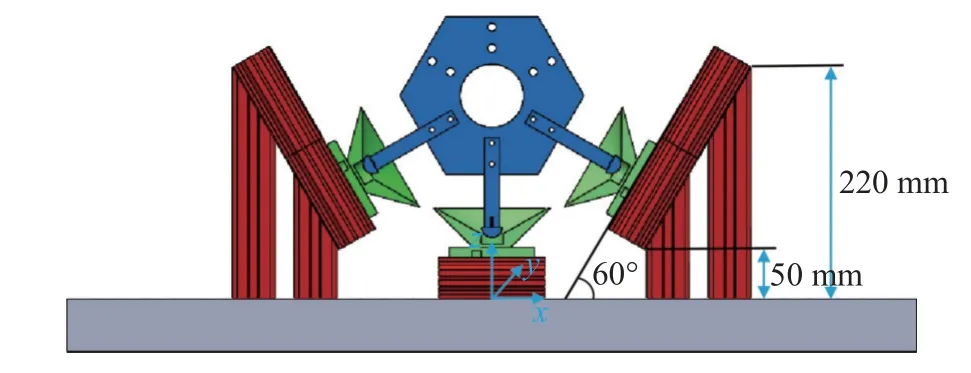
图24 对接模块布置及相关尺寸信息Fig.24 Specifications of the docking modules

3.3.2 柔顺对接实验

柔顺对接实验的目的是探究模型参考自适应阻抗控制方法的控制性能,具体实验步骤为:(1)启动机器人,使机器人运动至预组装位置;(2)设置控制器参数、末端移动期望轨迹和末端力期望值;(3)机器人携带待组装模块实施主动柔顺对接运动;(4)待组装模块到达指定组装位置完成对接,机器人停止运动.

机器人控制程序的具体流程图如图25 所示,首先初始化模型参数和碰撞参数,然后根据设置好的控制器参数和末端运动期望值,执行柔顺对接任务,通过实时的外力反馈来调整末端运动轨迹,当机器人外力超过碰撞极限阈值,或待组装模块到达指定组装位置,任务终止.

图25 柔顺对接实验流程图Fig.25 Flow chart of soft docking experiment

考虑到在实际对接情况下需要克服接触摩擦,并保证存在一定的对接力实现机械结构的锁紧,设定对接接触过程中存在z轴方向的期望力.沿z轴分别取阻抗参数md=0.1 kg,bd=20 N/(m·s-1),kd=400 N/m.在一对一接口对接情景下,采用模型参考自适应阻抗控制方法,对接的各个阶段如图26 所示.为探究算法的鲁棒性,分别设定对接接触过程中的期望力/力矩为Fd=[0,0,-8,0,0,0]T以及Fd=[0,0,-10,0,0,0]T,其末端接触力及末端位移输出曲线分别如图27 及图28 所示.

图26 一对一接口对接过程Fig.26 The docking process of single interface

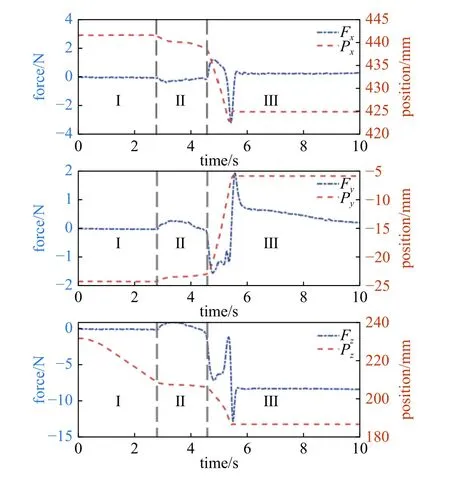
图27 一对一接口对接实验接触力及位移曲线(F zd=8 N)Fig.27 Contact force and displacement of single interface docking experiment (Fzd=8 N)

图28 一对一接口对接实验接触力及位移曲线(F zd=10 N)Fig.28 Contact force and displacement of single interface docking experiment (Fzd=10 N)

从图中可以看出,对接实验的曲线可分为3 个阶段.第I 阶段为接近过程,此阶段各个方向不存在接触情况,同时末端在z轴以一定轨迹向下运动.第II 阶段为接触初始阶段,此阶段对接杆末端与接纳锥锥面发生刚性碰撞,产生了一定的接触力,从而影响了z轴的向下位移,当接触力达到设定阈值(0.5 N),系统从运动控制模式切换为力控制模式,进入第III 阶段.基于本文中所描述的自适应阻抗控制算法,第III 阶段z方向的接触力向期望力靠近,同时各方向调整位移向对接锥孔移动,在经历过孔后,到达最终对接位置,z方向的接触力稳定在设定期望力.对比图27 和图28 可以发现,实验中对接的前两个阶段基本一致,第III 阶段也能够收敛到所设定的期望力附近,稳态力误差小,表明自适应方法能满足组装过程中力控制要求.

为验证算法的稳定性及鲁棒性,在设定z轴期望接触力为-8 N 的情景下,设计了3 组不同初始偏置下的对接实验.图29 展示了在不同初始偏置情形下的力变化曲线图,可以看出,在发生接触的第II 阶段,接触力均呈现向期望力收敛的趋势,尤其图29中蓝线(scenario B)和绿线(scenario C)均在第II 阶段就已收敛并稳定于期望力附近,且进入第III 阶段后,3 种情形的最终对接力都基本稳定于期望力.图30 展示了不同初始偏置情形下的机器人末端位移曲线,可以看出,对接杆最终均能准确落入在对接孔中.

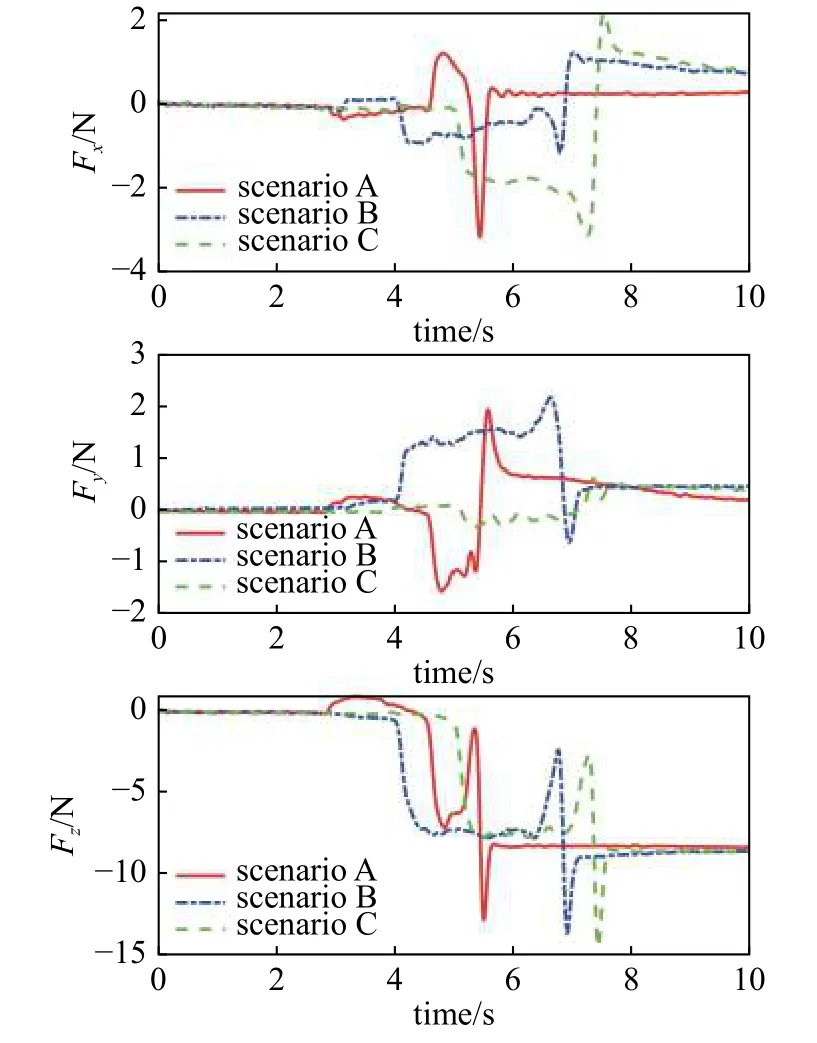
图29 不同初始偏置下一对一接口对接实验接触力曲线Fig.29 Contact force of single interface docking experiment under different biases

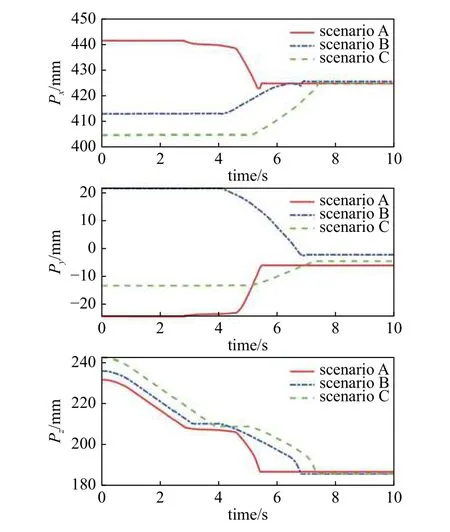
图30 不同初始偏置下一对一接口对接实验位移曲线Fig.30 Displacement of single interface docking experiment under different biases

在三对三接口对接情形下,由于实际工况存在零件加工及安装导致的误差,对接场景更为复杂,对接的各个阶段如图31 所示.当存在初始偏置时,对接过程中存在两种可能的接触现象.接触现象1 为单侧对接杆与锥面发生接触,而另一侧对接杆直至在过孔时才产生接触,在该接触现象下,为了使对接过程为沿起始接触一侧缓慢滑动至对接锥孔,设定对接过程中期望力/力矩分别为Fd=[0,0,-8,0,2,0]T及Fd=[0,0,-10,0,2,0]T,其中y轴的力矩设定主要为维持对接过程中的接触.基于自适应阻抗控制算法,其末端接触力及末端位移输出曲线如图32 及图33 所示.

图31 三对三接口对接过程Fig.31 The docking process of three interfaces

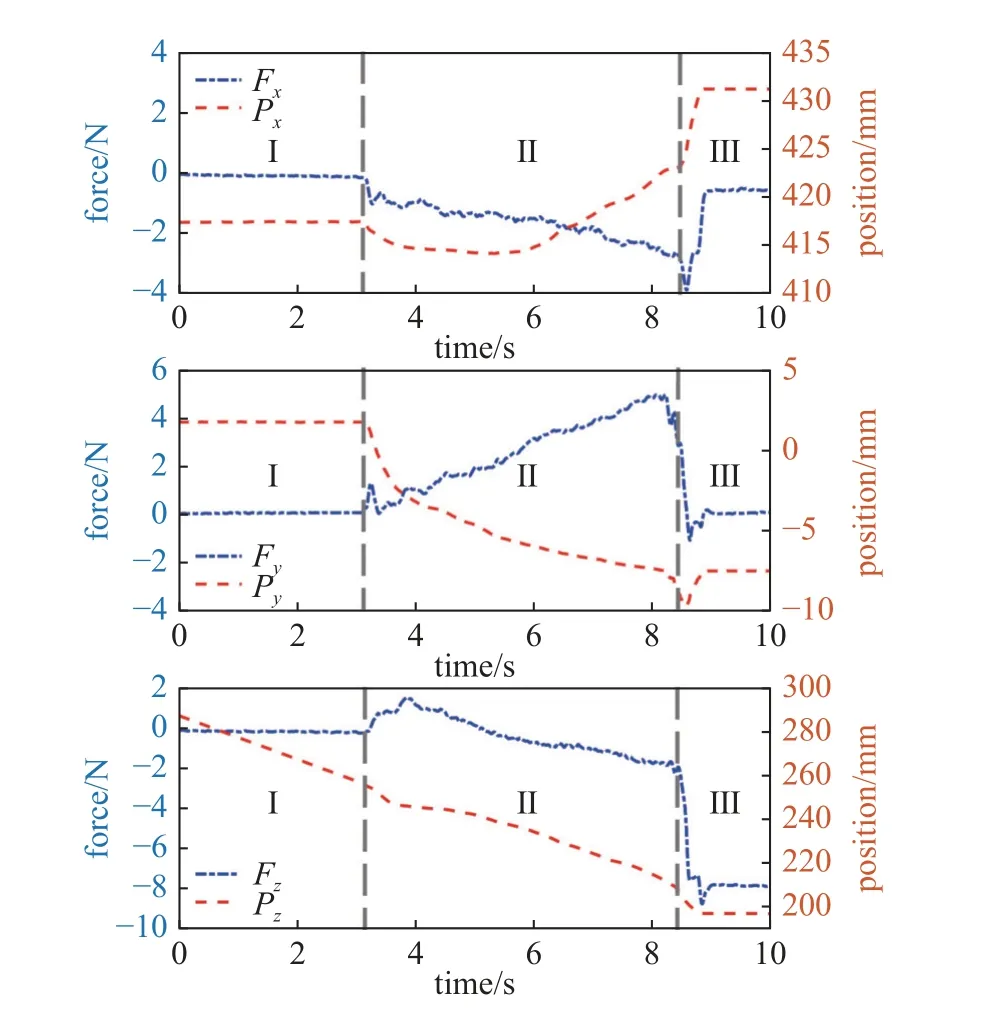
图32 三对三接口对接实验接触力及位移曲线(Fzd=8 N)Fig.32 Contact force and displacement of three interfaces docking experiment (Fzd=8 N)

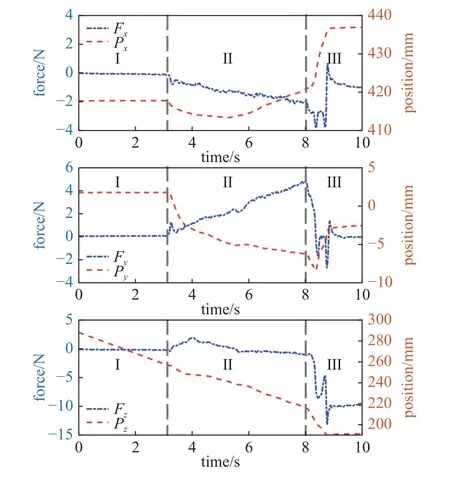
图33 三对三接口对接实验接触力及位移曲线(Fzd=10 N)Fig.33 Contact force and displacement of three interfaces docking experiment (Fzd=10 N)

可以看出,该接触现象下的对接实验也分为了3 个阶段,第I 阶段为接近过程,此阶段未发生接触.第II 阶段为单侧接触过程,由图24 中的接触面可知,当发生单侧接触时,因该侧接触面的面形导致难以产生很高的z轴的接触力,故该阶段z方向接触力缓慢增长,而x及y方向为保持接触导致受力逐渐增加;当接近对接锥孔时,另外两个对接杆与锥面发生接触,系统接触点增加,进入第III 阶段.第III 阶段中,各个方向开始调整位移向对接锥孔继续靠近,同时调整接触力向所设定期望接触力收敛,在经历过孔后,到达对接位置,且z方向稳定在设定期望力附近.对比图32 和图33 可以发现,在实验中,对接过程基本一致,第II 阶段接触力始终保持在较小范围内,但受模块结构及布置约束,尚未达到设定值,第III 阶段能够收敛到所设定的期望力,稳态力误差小,表明自适应阻抗控制方法能够满足组装过程中的力控制要求.

三对三接口对接时,可能出现的接触现象2 为起始状态为单侧对接杆与锥面发生接触,但在调整过程中为维持一定的接触力,对接杆突然沿z向快速运动,导致另一侧对接杆也与对接锥面发生接触并产生较大的接触力,然后通过两侧接触及力控方法调整,直至沿锥面滑落至对接孔,该现象下机器人的末端接触力及位移输出曲线如图34 所示.可以看出,该接触现象的对接过程分为了4 个阶段,第I 阶段为接近过程,此阶段未发生接触.第II 阶段为单侧接触过程,同接触现象1;当单侧难以保持接触时,对接杆下落,另一侧对接杆也与对接锥面发生碰撞,产生了一定的力及位移突变,进入第III 阶段.第III 阶段为多侧接触调整过程,此时z方向存在多个支撑点,故接触力向所设定期望接触力收敛,同时各个方向开始调整位移向对接锥孔靠近.在经历过孔后,进入第IV 阶段,此时各个对接杆经调整后到达指定位置,同时各方向受力稳定.

图34 三对三接口对接实验接触力及位移曲线(接触现象2)Fig.34 Contact force and displacement of three interfaces docking experiment (contact phenomenon 2)

因此,综合图32 及图34,在不同的初始偏置情况下,三对三的对接过程中可能产生不同的接触现象,而所设计的自适应阻抗控制算法均可实现在较小接触力范围内的稳定对接,由此证明了算法的稳定性和鲁棒性.

4 结论

本文以空间大型结构模块单元的在轨组装为背景,针对在轨组装复杂接触情形的建模问题,给出了空间机器人在轨组装的运动学和动力学方程,并推导了三维空间接触的动力学模型;针对多模块单元组装对接场景,采用了基于模型参考自适应的阻抗控制方法;最后进行了在轨模块组装的实验方法研究,搭建了飞行机器人模块组装对接仿真场景、飞行机器人地面实验气浮平台和模块组装柔顺对接实验平台,验证了飞行机器人的运动学和动力学模型的正确性,同时实验结果表明了自适应阻抗方法在多接口复杂接触情景下的有效性.需要注意的是,本文主要面向对接过程中利用固定基座的机械臂执行在轨组装任务场景,因此只讨论了基于自适应阻抗控制的多接口对接地面实验,而未呈现气浮条件的对接过程.但是,其他在轨任务,如利用自由飞行空间机器人捕获非合作目标、执行在轨加注或维修等,会涉及漂浮状态下的对接情形,如何实现漂浮状态下(气浮条件下)通过机器人的快速精确响应维持机器人与环境的接触力,值得后续深入讨论和研究.此外,本文主要聚焦于刚性小型模块组装过程的对接力控制和地面实验研究,尚未考虑结构柔性.然而结构柔性是影响在轨组装系统稳定性和精度的重要因素,如大尺寸或超大尺寸天线结构模块单元自身的结构柔性、空间机器人运输大负载单元模块的连杆柔性等,因此后续研究将在本文研究的基础上,进一步开展考虑结构柔性的在轨组装控制与实验研究.