深水隔水管-水下井口耦合系统双向涡激振动特性1)

胡鹏基 李朝玮 刘秀全 , 刘兆伟 畅元江 陈国明

* (中国石油大学(华东)机电工程学院,海洋油气装备与安全技术研究中心,山东青岛 266580)

† (常州大学石油与天然气工程学院,江苏常州 213164)

引言

深水隔水管-水下井口系统连接海面浮式平台与海底,是海洋油气勘探开发的咽喉[1-2].当海流流经隔水管-水下井口系统时会在其两侧产生交替泄放的漩涡,漩涡的周期性脱落致使深水隔水管-水下井口系统产生涡激振动(vortex-induced vibration,VIV),涡激振动是深水隔水管-水下井口系统疲劳失效的主要原因之一[3-5].如西设得兰海域的D534 钻井船作业时由于隔水管VIV 导致水下井口破坏,涡激疲劳破坏仅用时29 d.因此,VIV 分析对保障深水隔水管-水下井口系统作业安全至关重要[6-8].

深水隔水管-水下井口系统可以看作大长径比柔性立管结构,深水立管VIV 分析主要有模型试验与数值模拟两种方法,模型试验法的现象直观可靠但成本较高,而数值模拟法简单方便且成本较低,二者各有优势[9-12].数值模拟又可细分为CFD (computational fluid dynamics)仿真和经验模型仿真两种[13-14].CFD仿真分析精度较高但分析效率较低,经验模型仿真能简便可靠地体现尾流区的运动特征,因此通常将经验模型法作为深水隔水管VIV 分析的常用方法.目前的经验模型中,van der Pol 尾流振子模型可较好体现结构与流体之间的流固耦合特性而被广泛应用[15-16].Bishop 等[17-18]较早使用van der Pol 方程来描述VIV 作用在结构上的升力特性并命名为尾流振子.Hartlen 等[19]沿用该概念并发展了类似的振子方程来模拟圆柱体尾流运动特性.Facchinetti 等[20]研究了不同耦合项(位移、速度和加速度) 对van der Pol 尾流振子的影响,发现加速度耦合是描述结构周围尾流运动最合适的方法.此后van der Pol 尾流振子模型逐渐应用于生产柔性立管与钻井隔水管VIV 特性研究.Farshidianfar 等[21]提出一种改进的van der Pol 尾流振子模型用于分析弹性支撑的刚性立管的VIV 特性,该模型可以在更宽的质量阻尼比范围内准确预测隔水管VIV 响应.Kurushina 等[22]结合实验数据建立了一个van der Pol 尾流振子参数的校准模型库,通过调用库中参数可以更好地预测低质量阻尼比下的隔水管VIV 响应.Ulveseter 等[23]基于van der Pol 尾流振子模型分析了在均匀流及不规则波共同作用下柔性立管CF (cross-flow)及IL(in-line)方向的VIV响应并进行了实验验证.Zhang等[24]基于Van der Pol 尾流振子模型建立了深海采矿立管输送高速螺旋流的VIV 分析模型,研究了柔性立管输送直流和螺旋流时的VIV 动态特性.Prethiv Kumar 等[25]和Ge 等[26]基于van der Pol 尾流振子模型建立了柔性立管VIV分析模型,研究了剪切流作用下不同的长径比、弯曲刚度、质量比和轴向张力等对柔性立管VIV 响应的影响.Qu 等[27]和Xu 等[28]基于van der Pol 尾流振子模型分析了大长径比柔性立管在均匀流及剪切流中的VIV 特性并进行了对比验证,提出一种尾流振子模型参数校正方法.Xu 等[29]基于van der Pol尾流振子模型分析了钻井隔水管在均匀流中CF 及IL 方向的VIV 疲劳损伤,并研究了海流流速、顶部张力及结构外径对VIV 疲劳损伤的影响.Gao 等[30]和Gu 等[31]考虑轴向时变顶张力,基于van der Pol尾流振子模型分析了钻井隔水管在线性剪切流、指数剪切流、阶梯流中CF 及IL 方向的VIV 特性,随后研究了不同时变张力模型对VIV 响应的影响.Mao 等[32]基于van der Pol 尾流振子模型建立了考虑内部流体的钻井隔水管VIV 分析模型,分析了海流流速、海平面风速、顶部张力及钻井液排量对钻井隔水管的VIV特性的影响.以上的深水隔水管VIV 研究中通常将底端水下井口简化为固定约束.然而,水下井口与下部导管、表层套管等浅层井筒相连,浅层井筒承受非线性管-土耦合作用使水下井口产生循环振动,深水隔水管-水下井口系统实际振动更加复杂.非线性管-土耦合作用下的深水隔水管-水下井口耦合系统双向VIV 特性需要进一步研究.

本文在已有研究的基础上开展深水隔水管-水下井口系统VIV 研究.通过建立深水隔水管-水下井口耦合系统双向VIV 三维分析模型,考虑水下井口下部的管-土耦合作用,开展深水隔水管-水下井口系统顺流及横流向VIV 分析,得到深水隔水管-水下井口系统双向VIV 动力响应,揭示管-土耦合下深水隔水管-水下井口耦合系统双向VIV 特性,相关研究成果可为深水隔水管-水下井口系统VIV分析、设计及管理提供参考.

1 耦合系统涡激振动模型

1.1 深水隔水管-水下井口系统模型

深水隔水管-水下井口系统由上部挠性接头(upper flexible joint,UFJ)、隔水管、下部挠性接头(lower flexible joint,LFJ)、LMRP、BOP、水下井口(wellhead,WH)、导管及表层套管依次连接组成.为建立隔水管-水下井口系统的VIV 数学模型,以海平面位置隔水管圆心为原点建立三维笛卡尔坐标系,海流顺流向为x方向,H0为海平面以上高度,H1为海水深度,H2为土壤中管柱深度,具体如图1所示,并在VIV 数学模型建立过程中做如下假设:

图1 深水隔水管-水下井口系统示意图Fig.1 Deepwater riser/wellhead system

①各组成装备由均质的、各向同性的和线弹性的钢材制造;

② 系统内部充满钻井液,忽略钻头和钻柱影响;

③考虑浮力块、辅助管线对结构湿重和水动力外径的影响并做相应参数调整,但不考虑其对结构弯曲刚度的贡献;

④ 管柱系统可看作欧拉-伯努利梁模型,不考虑其扭转变形;管柱在自重和外载荷的影响下横向偏移和转角较小;

⑤ 本文研究管-土耦合下VIV 振动,只考虑海流与土壤对结构的影响,未考虑顶部钻井平台运动及波浪动载荷;

⑥ 系统运动过程中周边土壤未发生液化,未考虑土壤附加阻尼影响.

根据欧拉-伯努利梁理论,系统运动控制方程可表述为[33-34]

式中,x和y分别为IL 及CF 方向的坐标;z为竖向坐标;t为时间;m为系统单位长度质量[29];cs为结构阻尼系数;cfx与cfy分别为IL 及CF 方向的流体阻尼系数[35];EI为抗弯刚度;T为有效轴向张力;Fx和Fy分别为IL 及CF 方向水动力载荷.

流体阻尼系数cfx与cfy的计算方法如下[36]

式中,γv为动力黏度系数;ωf为漩涡脱落频率;ρs为海流密度;Dh为结构水动力外径.

参数γv与ωf分别可表示为[37]

式中,CDS为稳态拖曳力系数;St为斯托哈尔数;Vr为IL 方向结构相对海流速度;Vc为海流流速;Vxy为IL 方向结构振动速度.

有效轴向张力T可表示为

式中,Ttop为顶部张紧力;mr与mf分别为系统结构浸没在水中的质量与系统内部流体质量;g为重力加速度;TTR为顶部张紧系数;Ws为系统总重力.

深水隔水管-水下井口系统的边界条件为[38]

式中,Ku为上挠性接头转动刚度.

1.2 涡激水动力载荷模型

使用美国船级社推荐方法计算海流剖面,某深度海流流速Vc可表示为风致流速与潮流速度之和,即[32]

式中,Vcw为风致海流流速;Hf为风致动摩擦力可达最大深度;Vct为近海面潮流速度.

Vcw与Hf可由埃克曼漂移理论得到,表示为

式中,Vw为近海面风速;φ为纬度坐标.

当海流流经深水隔水管-水下井口系统某一截面时会在CF 方向产生脉动的涡激升力FL,在IL 方向产生脉动的拖曳力FD与稳态的拖曳力FDS,如图2 所示.

图2 涡激振动水动力载荷Fig.2 VIV hydrodynamic load

其中,脉动涡激升力FL与脉动拖曳力FD由漩涡脱落引起,而稳态拖曳力FDS则由稳态海流引起,三者可表示为[39-40]

式中,CL与CD分别为脉动升力系数与脉动拖曳力系数.

系数CL与CD可表示为[41-42]

式中,CL0与CD0分别为固定圆柱的升力系数与拖曳力系数;p与q分别为横流与顺流向的尾流变量参数.

使用van der Pol 方程来描述深水隔水管-水下井口IL 及CF 方向的尾流运动特性,可表示为[43]

式中,εx,εy,Ax与Ay为无量纲耦合系数.

因此,IL 及CF 方向涡激水动力载荷可表示为

1.3 土壤抗力模型

处于泥线以下的结构发生弯曲变形会受到水平方向的土壤抗力,本文使用API 规范中推荐的砂土p-y曲线法对侧向土壤抗力进行模拟[44].泥线下坐标z处的竖向极限承载力pu可表示为

式中,C1,C2与C3为与摩擦角相关的无量纲参数;γz为土体有效容重;-z-H1为泥线以下当前位置到泥线深度;Ds为管柱结构外径.

IL 及CF 方向的侧向土壤抗力可表示为[45]

式中,Au为修正系数,当结构受循环载荷时,Au=0.9;Kini为土抗力初始刚度.

2 数值方法及模型验证

2.1 数值方法

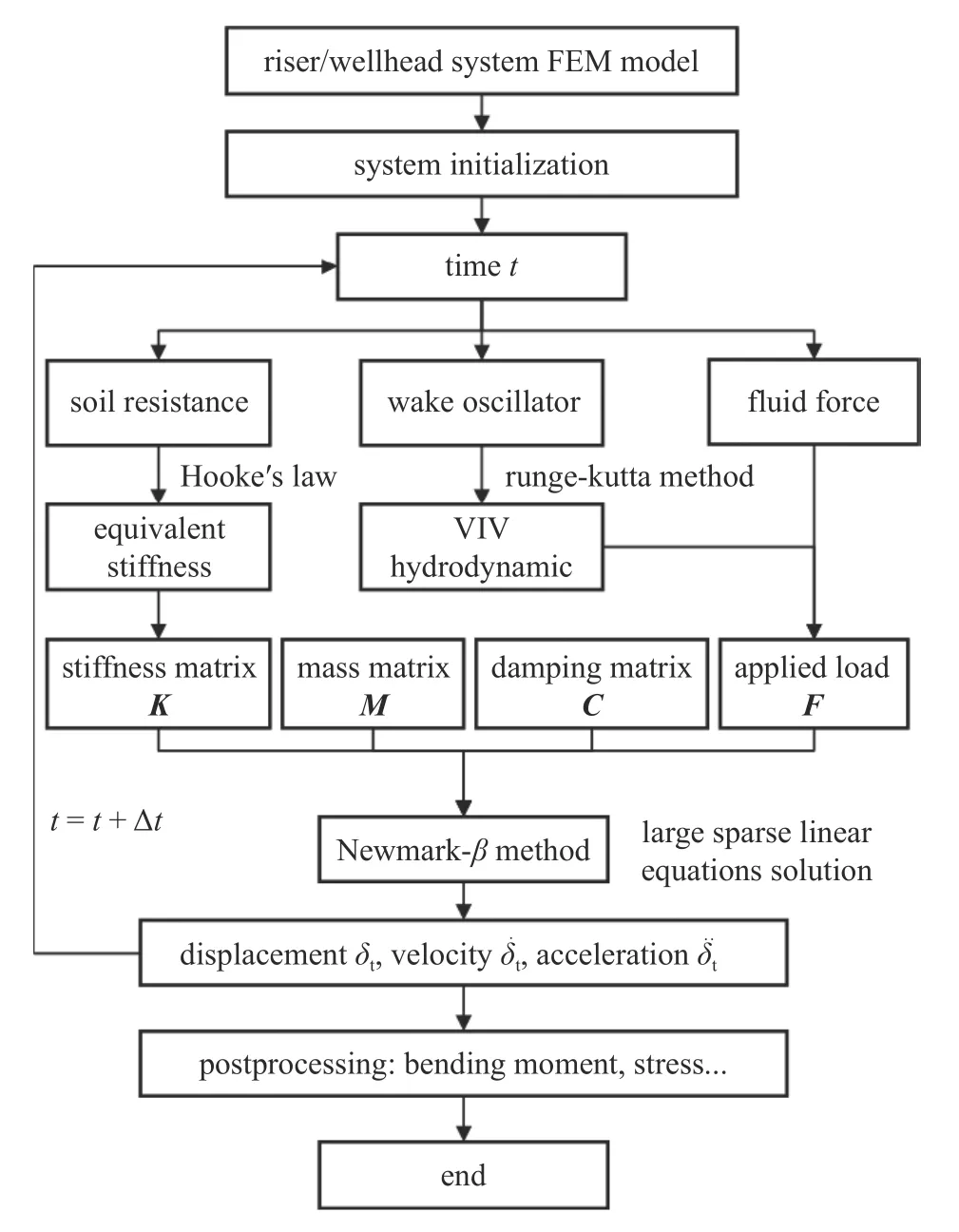
图3 涡激振动分析流程Fig.3 VIV analysis procedure

深水隔水管-水下井口系统单元离散采用的方法为一致插值算法,单元类型为三维梁单元,离散后深水隔水管-水下井口耦合系统结构动力学方程可表示为

式中,M,C与K分别为深水隔水管-水下井口系统质量、阻尼和刚度矩阵;与δ分别为深水隔水管-水下井口系统加速度、速度和位移向量;F为外部载荷向量.其中,系统质量矩阵M、刚度矩阵K分别由结构单元质量矩阵、单元刚度矩阵组装得到.侧向土壤抗力不直接施加在浅层井筒上,而是根据胡克定律得到等效土壤刚度叠加在对应的浅层井筒单元刚度矩阵中,等效土壤刚度随结构横向偏移而改变,

如图4 所示.系统阻尼矩阵C的结构阻尼部分由瑞利阻尼计算方法得到,如下式所示.瑞利阻尼矩阵cs于有限元动态分析之初确定,不将系统刚度矩阵K中等效土壤刚度的动态变化考虑在内.

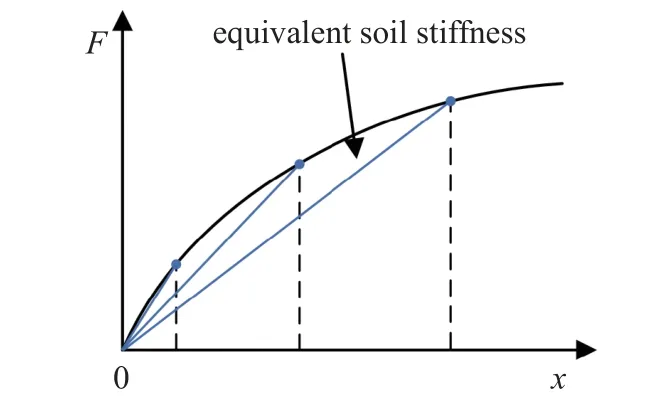
图4 等效土壤刚度曲线Fig.4 Equivalent soil stiffness curve

式中,α与β为比例系数.

在深水隔水管-水下井口系统VIV 分析的每个迭代步都需要与尾流振子模型进行交互,获得尾流变量参数p和q来计算下一迭代步的涡激升力及拖曳力.van der Pol 尾流振子方程为二阶常微分方程,本文先对其进行降阶处理,随后使用4 阶龙格库塔法进行求解,降阶的方程如下式所示.

使用Newmark-β法进行有限元模型迭代求解时,每个迭代步都需要求解与系统等效刚度矩阵相关的大型稀疏线性方程组,减小线性方程组求解时间可以提高VIV 分析效率.由于约束后的系统刚度矩阵为对称正定矩阵,因此本文使用iCholesky 分解与预条件共轭梯度法结合的方式进行大型稀疏线性方程组求解

在后处理中,深水隔水管-水下井口系统在IL及CF 方向的弯矩可表示为[30]

式中,Mx与My分别为系统IL 及CF 方向的弯矩.

商代社会已经出现家族应该是肯定，何景成先生在《商周青铜器族氏铭文研究》一书里，对商周时期的一些族氏进行了研究，其中就有诸好戈族、史族、息族等。那么，如果我们说殷商有一个独立的“子族”家族，是否具有了一定的合理性呢？即“子某”类型的称谓包括两种人，一种是诸“王子”，一种是“子族”人。把同是“子某”类型称谓中的一部分从“王子”中分离出来，独立为“子族”，也许上面的一些问题就很好解释了。卜辞中不属于“王族”的“子族”实际上就是殷商时期的独立“子族”家族；“子族”祭祀自己的祖先，因此有相对独立而集中的祭祀对象。

深水隔水管-水下井口系统结构及尾流振子初始条件如下

2.2 模型验证

本文通过与Gao 等[46]计算结果、Prethiv 等[37]数值分析结果及Holmes 等[47]CFD 分析结果进行对比来验证所建模型及分析方法的合理性,所得模型对比结果如图5 所示.由图5(a)可知,本文模型所得结果与Gao 等数值分析结果具有较好的一致性,系统VIV 的横流向RMS 位移曲线基本吻合.由图5(b)可知,本文结果与Prethiv 等[37]数值分析结果和Holmes 等CFD 分析结果具有较好的一致性,系统横流向RMS 位移曲线中的波峰波谷位置基本相同,驻波及行波特性基本相符,与CFD 计算结果偏差稍大,这是因为CFD 仿真模型与半经验模型求解方法本身存在差别.综上所述,本文模型分析结果可以定性及定量地描述深水隔水管VIV 特性,可用来进行后续的深水隔水管-水下井口系统双向VIV 特性分析.同时,本文所建立模型的优点将在后文分析与讨论部分通过对比底部固支及考虑管-土耦合作用的隔水管-水下井口系统VIV 响应结果进行阐述.

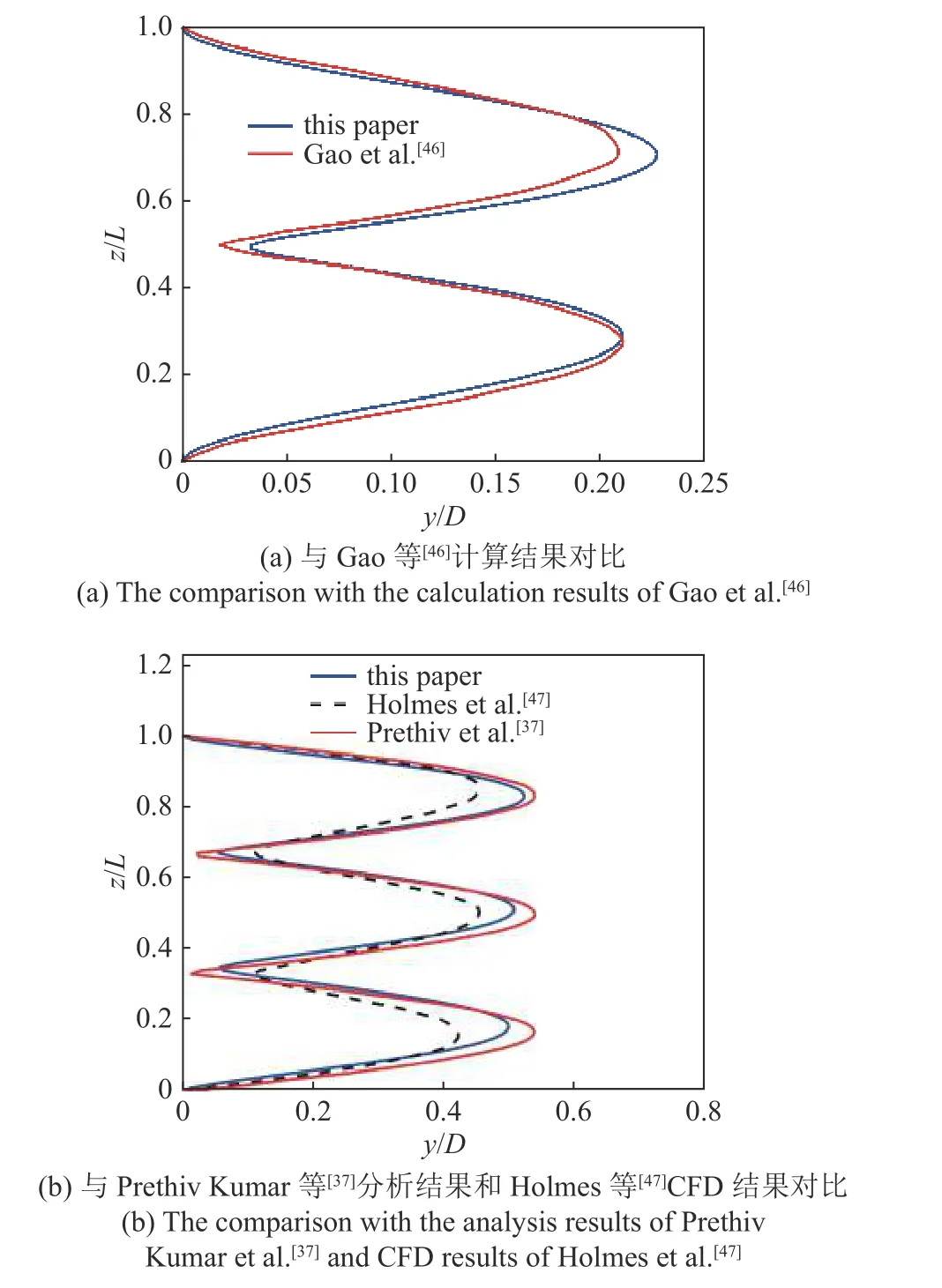
图5 模型验证Fig.5 Model verification

3 分析与讨论

3.1 基本参数

本文进行VIV 分析所用的深水隔水管-水下井口系统结构参数见表1,所使用的土壤参数为南海某海域土壤参数[45],见表2.深水隔水管-水下井口系统配置见表3.深水隔水管-水下井口系统全长1256.2 m,划分单元共1205 个,分析步长0.05 s.由式(8)及式(9)所得海流剖面如图6 所示,表面海流流速分别为0.55,0.75,0.95 和1.15 m/s.海底泥线位于水面以下-1086 m 处.

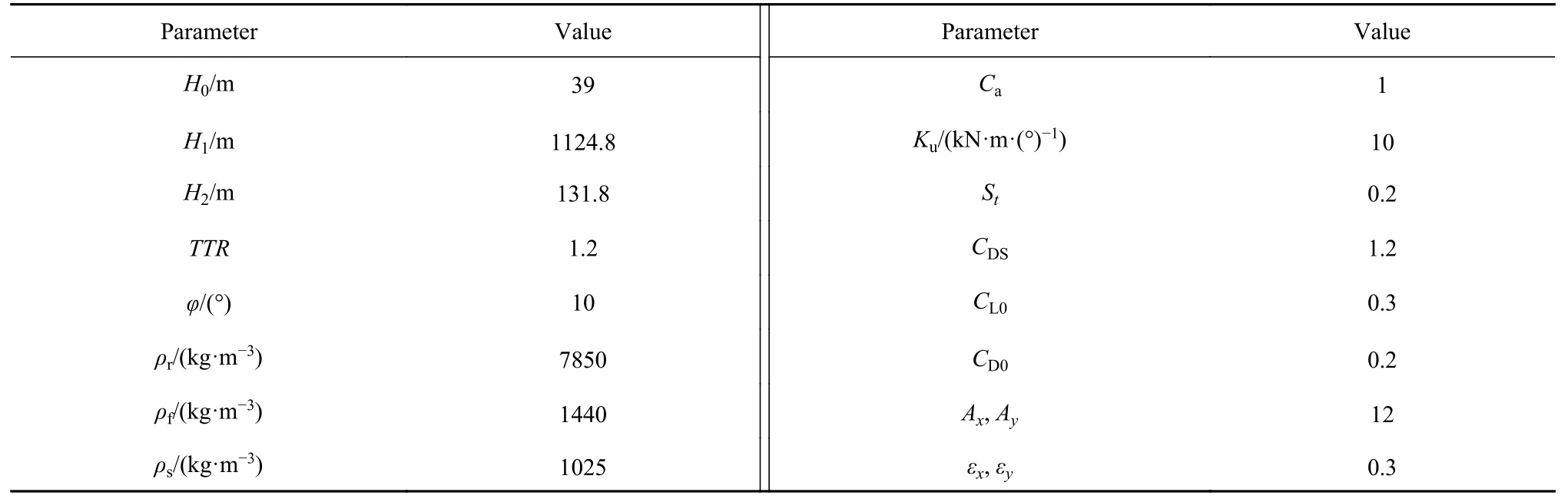
表1 深水隔水管-水下井口系统参数Table 1 Deepwater riser/wellhead system parameters

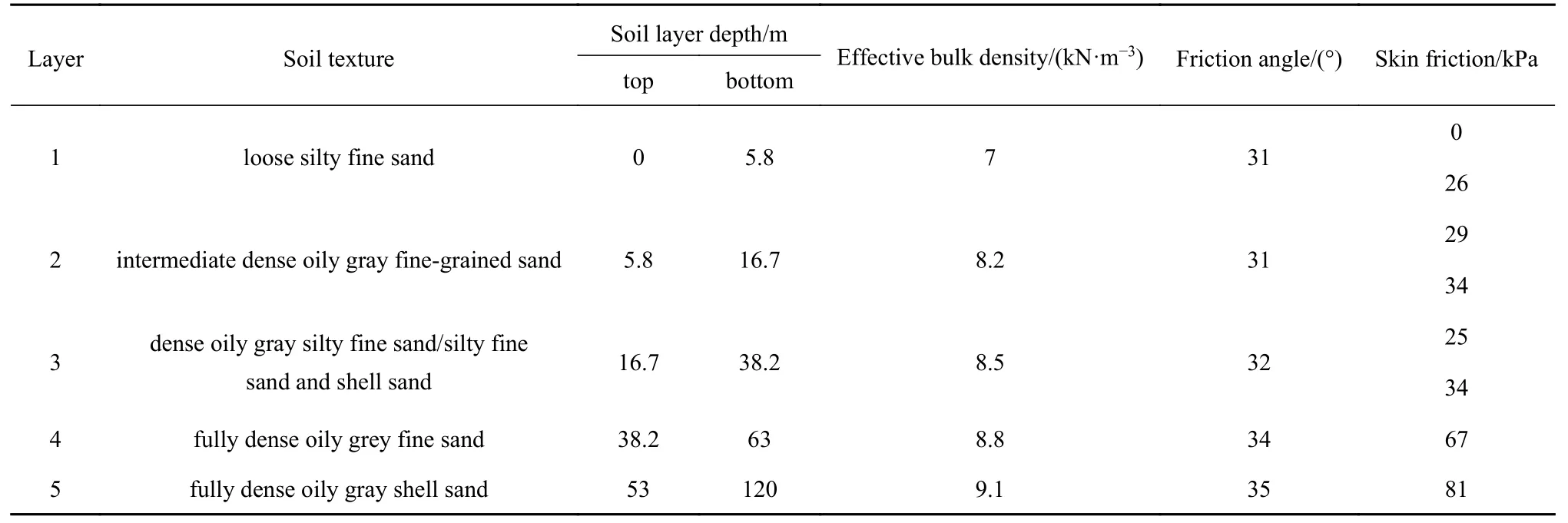
表2 土壤参数Table 2 Soil parameters

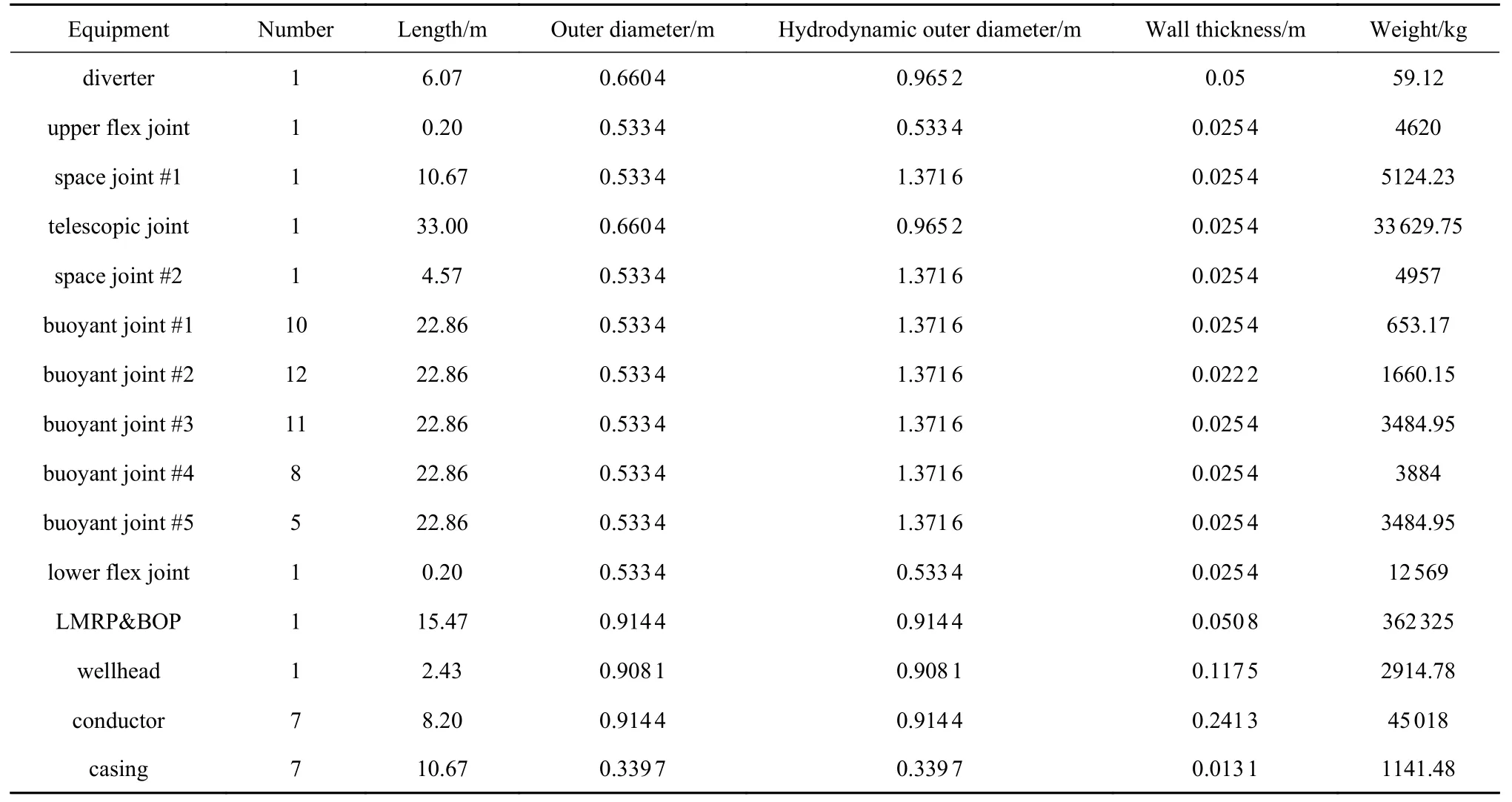
表3 深水隔水管-水下井口系统配置Table 3 Deepwater riser/wellhead system configuration

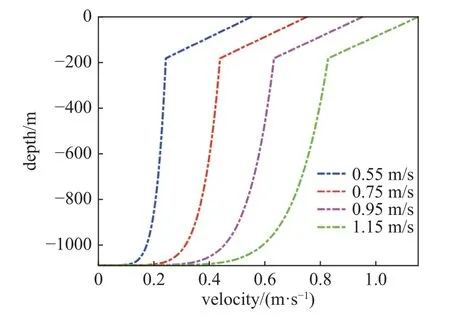
图6 海流剖面Fig.6 Current profile

3.2 VIV 响应特性分析

考虑管-土耦合前后所得深水隔水管-水下井口系统前6 阶固有频率对比见表4.由于深水隔水管-水下井口系统横截面为对称圆截面,其模态分析所得模态频率通常成对出现,因此表中所比较的为顺流方向的前6 阶模态振型所对应的模态频率.相比于底部固支约束,管-土耦合下的隔水管-水下井口系统研究需要额外考虑泥线以下的导管及套管,导管及套管的加入增加了系统结构长度,使系统质量增大,整体刚度减小,造成考虑管-土耦合的深水隔水管-水下井口系统固有频率降低.

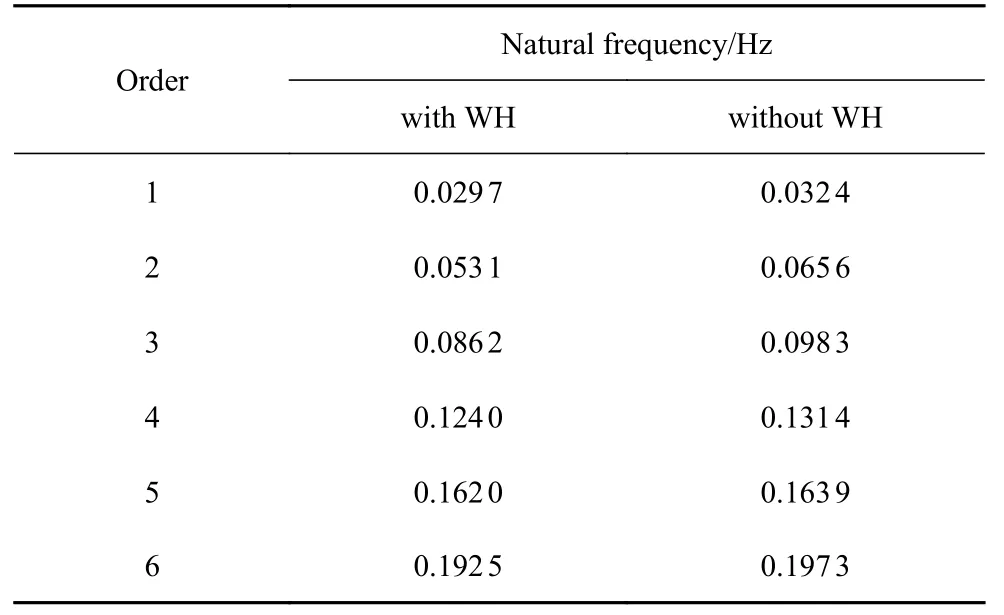
表4 前6 阶固有频率对比Table 4 The comparison of the first 6 natural frequency

图7 为表面流速0.95 m/s 下深水隔水管-水下井口系统在CF 及IL 方向的RMS 位移.由图7(a)可知,表面海流流速为0.95 m/s 时,CF 方向VIV 响应的主导模态表现为4 阶,RMS 位移最大值在水面以下-1000 m 处.系统RMS 位移呈现出对称特征,且系统下半部分的RMS 位移偏大.考虑管-土耦合后,水下井口处由固支约束弱化为由土壤弹力提供的微幅循环振动,CF 方向水下井口附近的RMS 位移明显增加,隔水管-水下井口系统刚度减小,由此造成系统整体RMS 位移都有不同幅度的增加,其中,CF 方向RMS 位移曲线各个极大值处的增加幅度较大.隔水管-水下井口系统刚度减小造成系统固有频率降低,但由于降低幅度较小,隔水管-水下井口系统在CF 方向的RMS 位移表现出的模态振型有些许变化但主导模态振型没有改变.由图7(b)可知,深水隔水管-水下井口系统IL 方向的RMS 位移没有表现出明显的VIV 特征,原因是在IL 方向深水隔水管-水下井口系统整体所受稳态拖曳力FDS比脉动拖曳力FD要大得多,使得IL 方向隔水管-水下井口系统以静态变形为主.考虑管-土耦合后,受水下井口处约束弱化的影响,深水隔水管-水下井口系统IL 方向的RMS 位移增大,但由于系统IL 方向的静态变形较大,因此系统RMS 位移的增加幅度不明显.

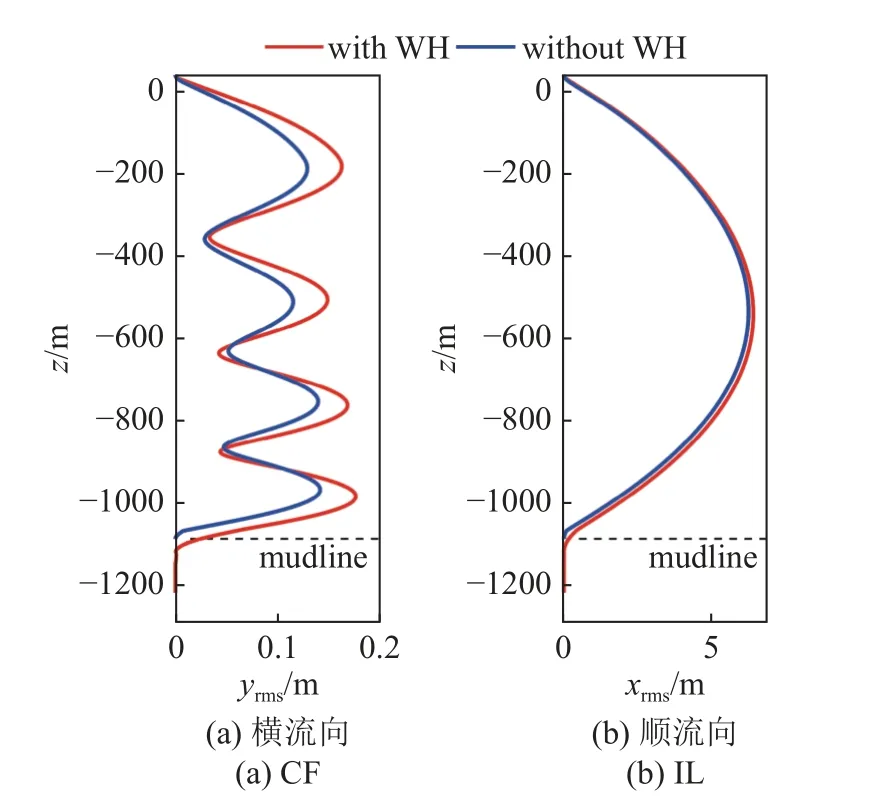
图7 表面流速0.95 m/s 下的均方根位移Fig.7 RMS displacement with the surface velocity of 0.95 m/s

图8 为表面流速0.95 m/s 下深水隔水管-水下井口系统中点在CF 及IL 方向的时域振动曲线.由图8(a)可知,系统CF 方向的VIV 位移响应在0 位置附近循环振动,考虑管-土耦合后,系统CF 方向的VIV 位移响应振幅有明显的增大.由图8(b)可知,系统IL 方向的位移响应在受静态海流力影响产生的静态变形的基础上做循环振动,振动幅度较小,考虑管-土耦合作用对IL 方向VIV 位移响应整体偏移较大,对VIV 位移响应振动幅值影响较小.

图8 表面流速0.95 m/s 下的系统中点位移Fig.8 Displacement of system midpoint with the surface velocity of 0.95 m/s

将深水隔水管-水下井口系统位移响应做傅里叶变换得到位移幅频曲线,提取位于-112.98,-268.85,-424.71,-580.58,-736.44,-892.30 和-1048.17 m 处CF 与IL 方向的位移幅频曲线如图9 所示,其中蓝色虚线及彩色实线分别为考虑管-土耦合前及考虑后的幅频曲线.由图可知,CF 方向的深水隔水管-水下井口系统振幅分布与主导模态振型对应.IL 方向振动频率约为CF 方向振动频率的2 倍,之所以存在些许偏差是由于计算漩涡脱落频率时考虑了隔水管-水下井口系统与海流的相对速度.考虑管-土耦合作用后,深水隔水管-水下井口系统CF 及IL 方向的振幅增大,振动频率减小,其中水下井口附近的振幅变化较为明显,其他位置的幅频变化规律与水下井口处相同但变化幅度较小.

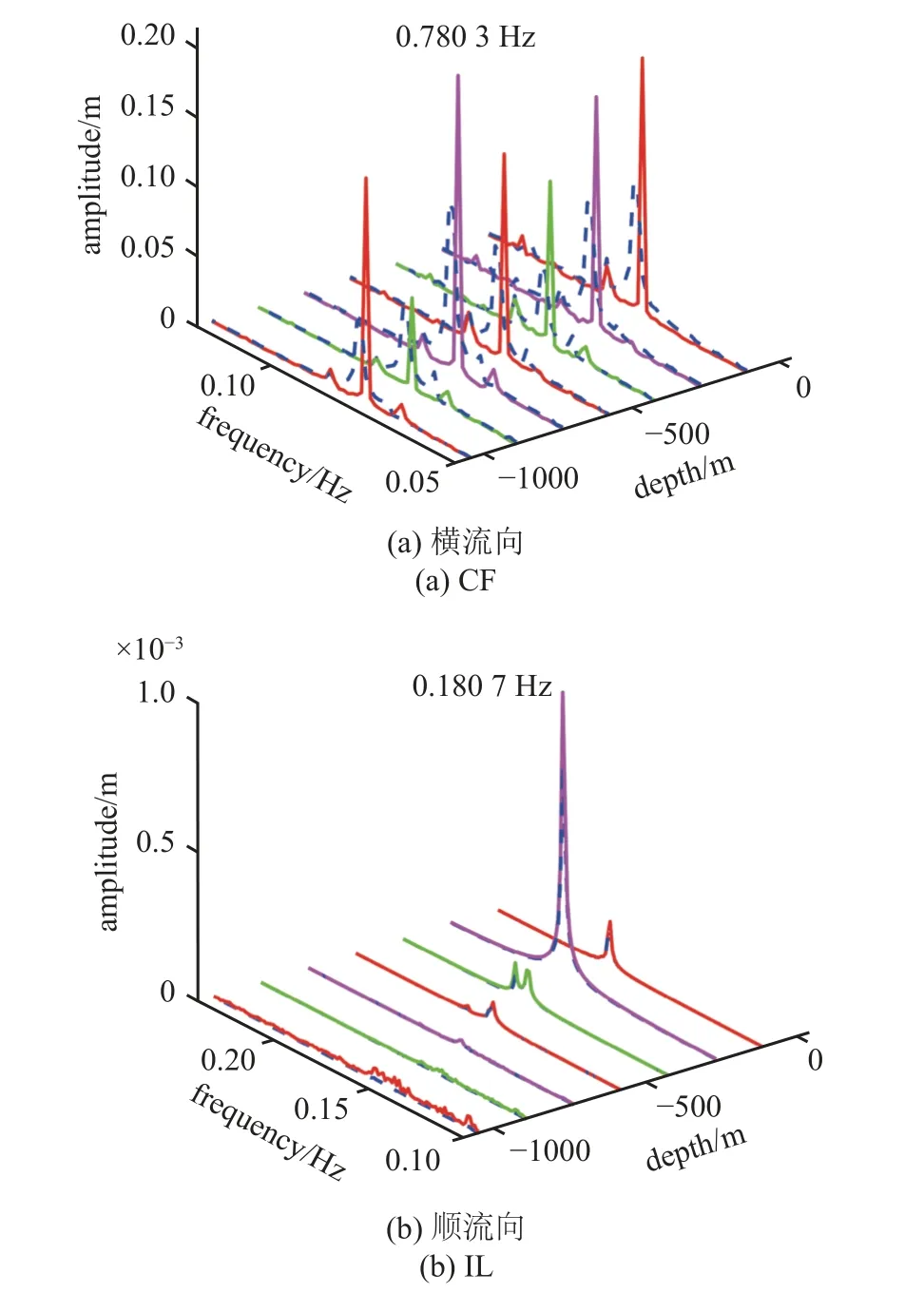
图9 表面流速为0.95 m/s 下位移幅频曲线Fig.9 Amplitude-frequency curves of displacement with the surface velocity of 0.95 m/s

提取深水隔水管-水下井口系统VIV 分析稳定后的弯矩,取其最大绝对值,得到深水隔水管-水下井口系统CF 与IL 方向的弯矩分布,如图10 所示.由图可知,深水隔水管-水下井口系统IL 方向的弯矩大于CF 方向弯矩,且两方向的弯矩最大值都位于深水隔水管-水下井口系统近泥线处.考虑管-土耦合作用后,泥线附近约束弱化,表面流速为0.95m/s 下CF 方向的弯矩最大值由314.86 kN·m 增大至519.87 k N·m,最大值位置由泥线以上-1085.92 m 降低至泥线以下-1099.52 m,IL 方向弯矩最大值由1931.76 kN·m 增大至2387.15 kN·m,最大值位置由-1085.92 m 降低至-1098.49 m,CF 与IL 方向的弯矩变化较为明显.

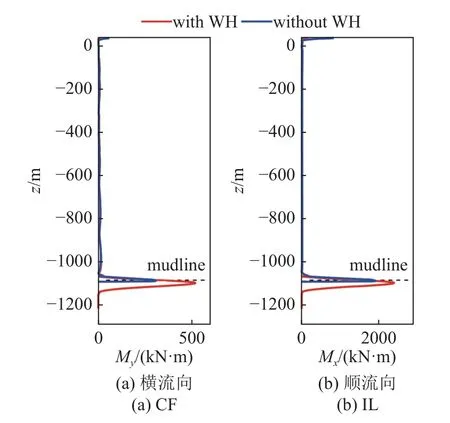
图10 表面流速为0.95 m/s 下横流及顺流向弯矩Fig.10 Bending moment with the surface velocity of 0.95 m/s in the CF and IL directions

3.3 VIV 影响因素分析

以海流剖面为变量研究了海流流速对深水隔水管-水下井口系统VIV 特性的影响,采用的海流剖面如图6 所示,其余系统参数不变.图11 为不同海流流速下深水隔水管-水下井口系统CF 及IL 方向的RMS 位移.由图可知,表面海流流速分别为0.55,0.75 及0.95 m/s,系统CF 方向的VIV 位移响应表现的主导模态分别为2 阶、3 阶与4 阶.表面海流流速为1.15 m/s 时,系统位移响应处于5 阶模态的过渡状态.因此,海流流速越高,则系统CF 方向VIV振动的主导模态阶数越高.系统IL 方向的RMS 位移随海流流速的增加而增大,且RMS 位移最大值都位于系统中部.

图11 不同海流流速下横流及顺流向的均方根位移Fig.11 RMS displacement in the CF and IL directions with different current velocity

图12 及图13 分别为不同海流流速下深水隔水管-水下井口系统中点CF 及IL 方向的时域轨迹及幅频曲线.由图可知,系统振动频率与海流流速呈正相关,且系统CF 及IL 方向振动频率的2 倍关系不会因为海流流速的不同而发生改变.系统CF 方向的振动幅值与所在海流流速下系统的主导振型有关,位于主导振型波峰位置的系统节点具有更大的振幅.由于系统所受的脉动拖曳力较小,系统IL 方向的振动幅值较小,但海流流速对IL 方向VIV 振幅的影响不可忽略.

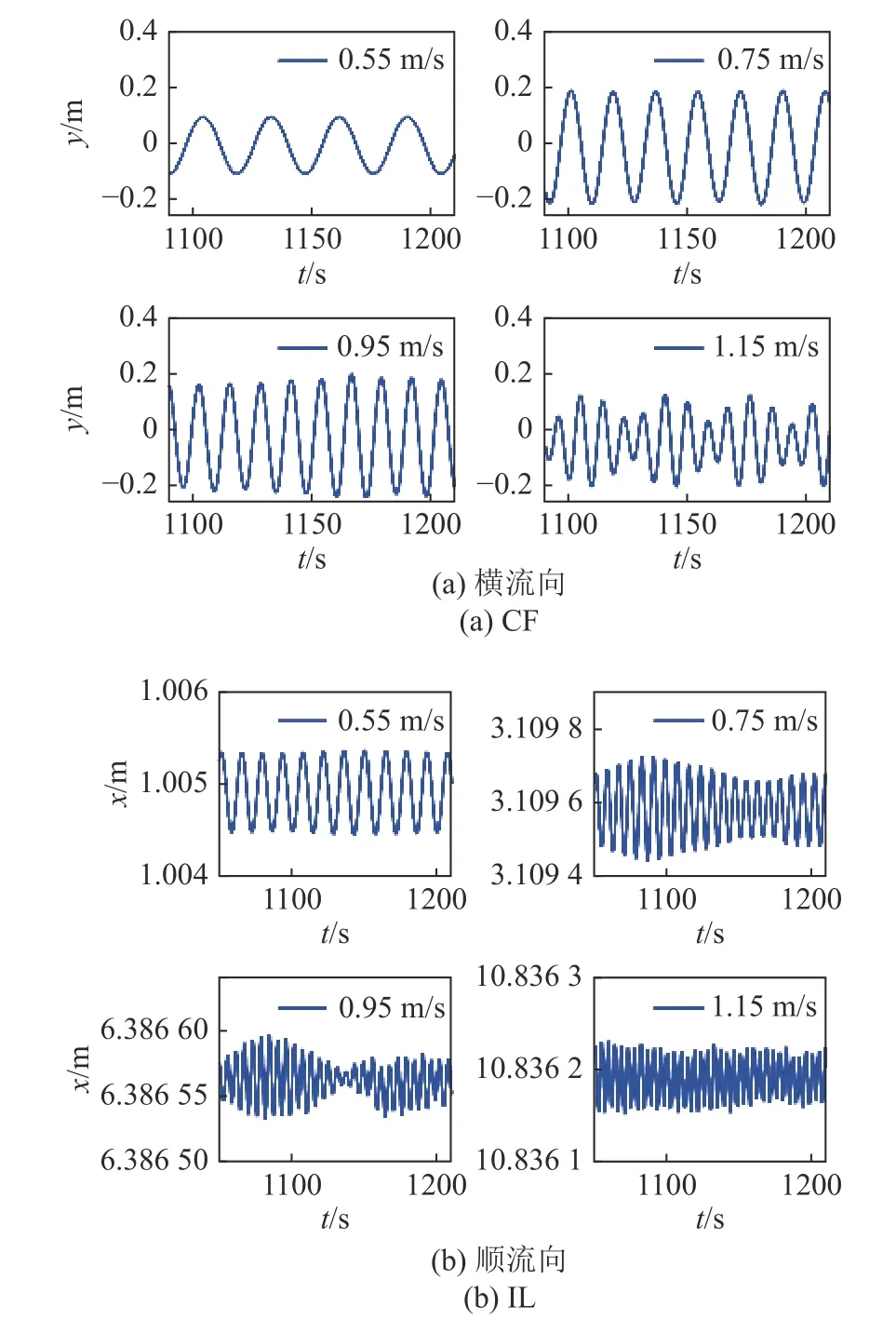
图12 不同海流流速下系统中点的横流及顺流向位移Fig.12 Displacement of system midpoint in the CF and IL directions with different current velocity

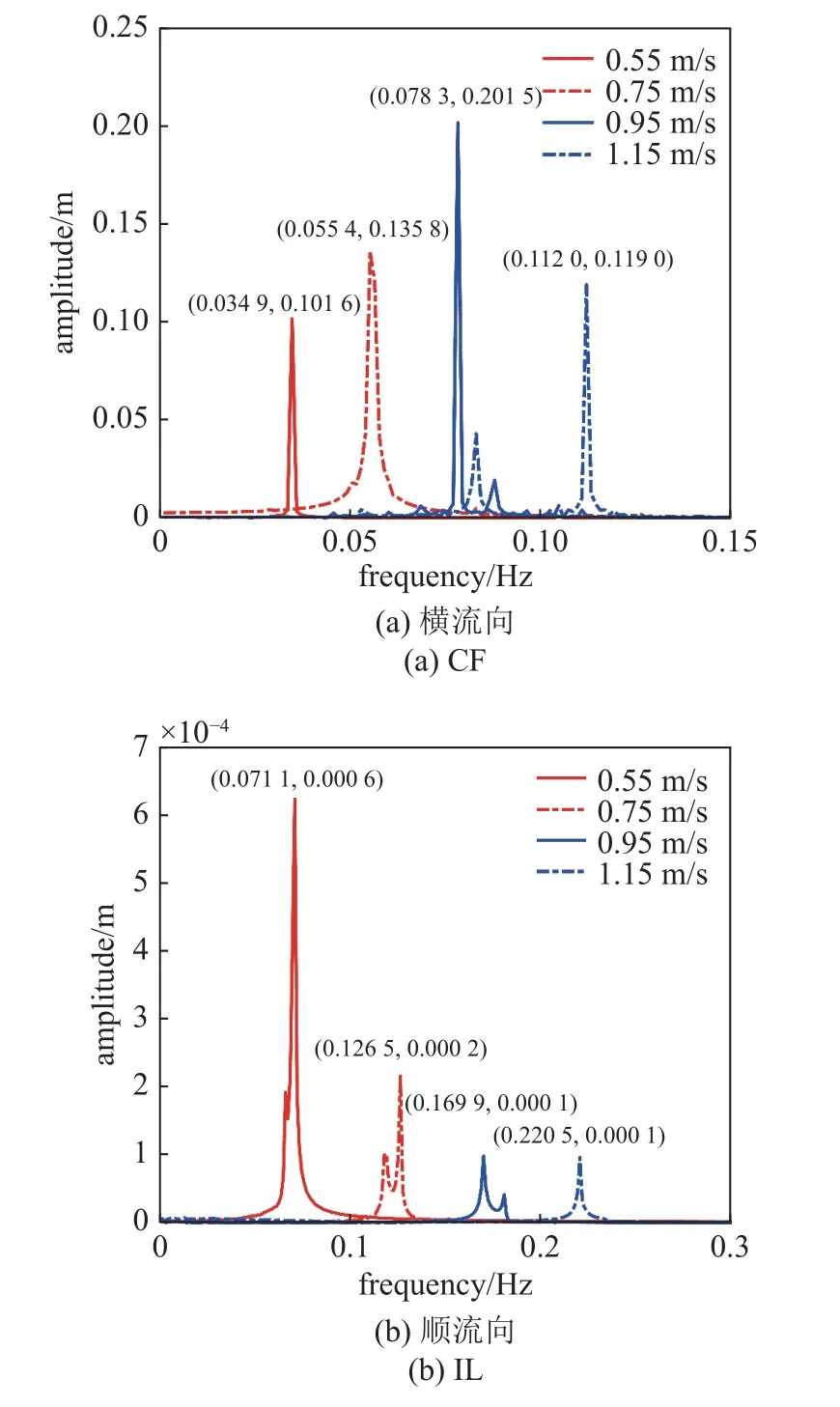
图13 不同海流流速下系统中点幅频曲线Fig.13 Amplitude-frequency curves of system midpoint with different current velocity

图14 为不同海流流速下深水隔水管-水下井口系统CF 及IL 方向的弯矩.由图可知,系统CF 及IL 方向的弯矩与海流流速呈正相关.海流流速越高,由海流流速增加导致的系统CF 方向弯矩变化越小,而系统IL 方向的弯矩变化越大.系统CF 及IL方向的弯矩最大值一直处于泥线以下-1099.52 m附近,且最大值位置一般不随海流流速的增加而改变.较大的弯矩使泥线附近的系统结构产生更大的弯曲应力,因此,进行深水隔水管-水下井口系统VIV分析应重点关注泥线附近的系统振动特性.

图14 不同海流流速下横流及顺流向弯矩Fig.14 Bending moment in the CF and IL directions with different current velocity

以土壤侧向极限抗力为变量研究了土壤硬度对深水隔水管-水下井口系统VIV 特性的影响,基于表2 的土壤数据,加入土壤抗力增幅系数并分别设定为0.5,1,2 及5,得到4 种不同硬度的土壤.图15中的0.5,1,2 及5 Ks 表示4 种不同硬度的土层可提供的侧向极限抗力,其中,1 Ks 表示表2 中的土壤参数可提供的侧向极限抗力;0.5 Ks 表示一种较松软的土壤可提供的侧向极限抗力,该极限抗力为1 Ks 的一半;2 Ks 和5 Ks 分别表示更坚硬的土壤可提供的侧向极限抗力,该极限抗力分别为1 Ks 的2 倍及5 倍.

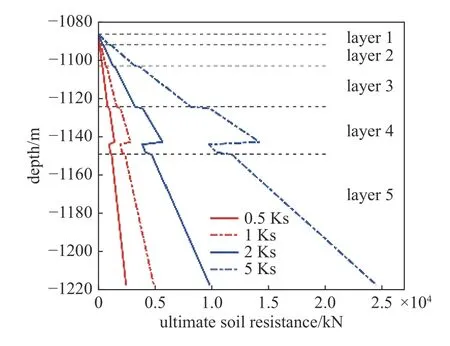
图15 土壤侧向极限抗力Fig.15 Soil lateral ultimate resistance

图16 表示不同土壤硬度对深水隔水管-水下井口系统CF 及IL 方向RMS 位移的影响.由图可知,土壤硬度变化对系统RMS 位移的影响较小,这是由于近泥线处的土壤侧向极限抗力变化较小,土壤硬度变化使土壤额外附加的等效刚度较小,而系统结构刚度与土壤附加的初始等效刚度较大,因此土壤额外附加的等效刚度在系统总刚度中的占比较低.

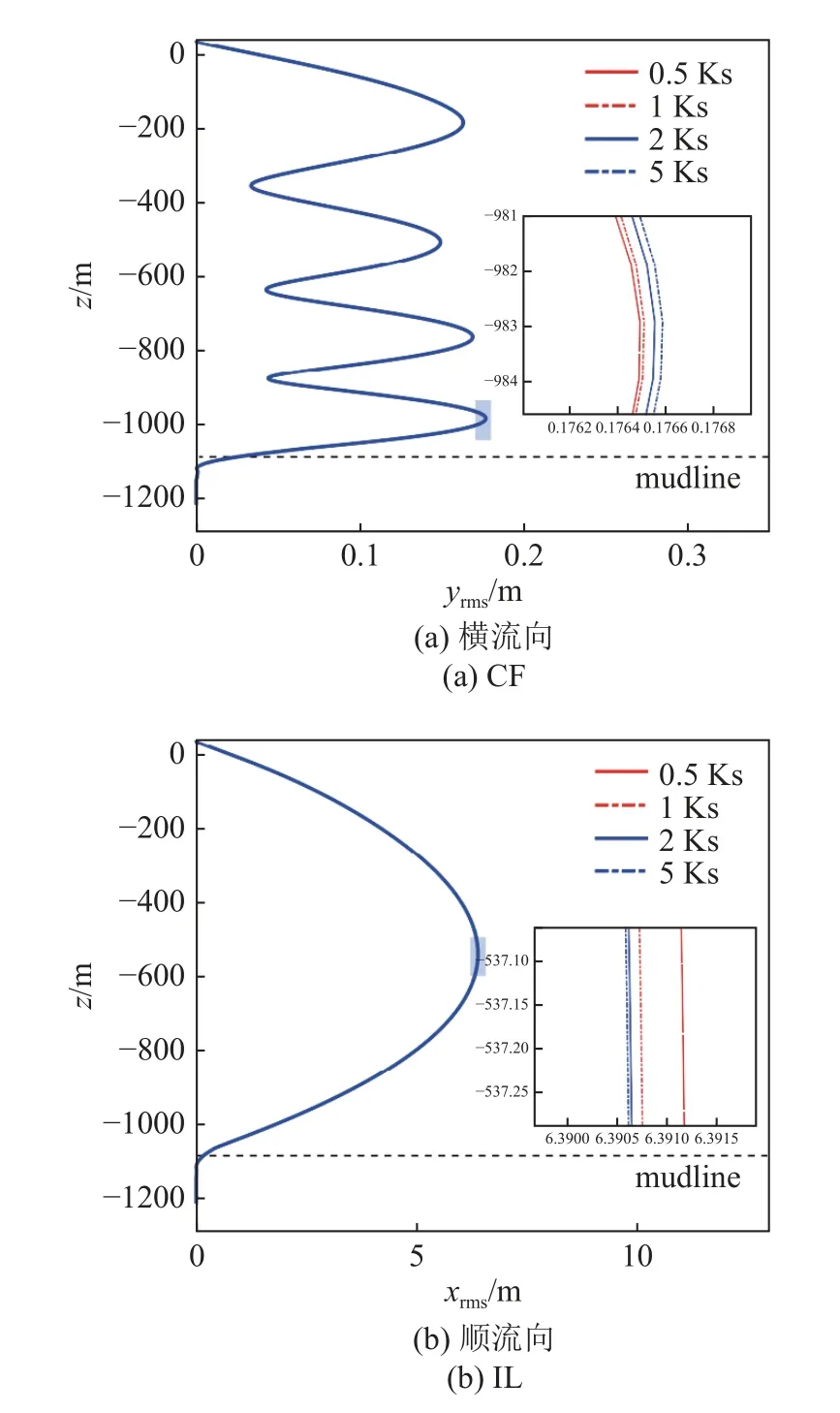
图16 不同土壤硬度下横流及顺流向的均方根位移Fig.16 RMS displacement in the CF and IL directions with different soil hardness

图17 为不同土壤硬度下深水隔水管-水下井口系统中点CF 及IL 方向的时域轨迹.由图可知,土壤硬度增加,系统整体刚度增大,系统CF 方向的振动幅值及IL 方向的平均位移减小.由于土壤抗力具有非线性特征,因此土壤硬度越大,则土壤侧向抗力增加量越小,土壤硬度变化产生的额外附加等效刚度越小,系统IL 方向的平均位移的变化量逐渐减小.

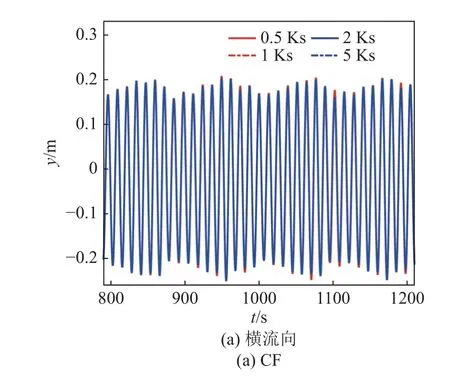
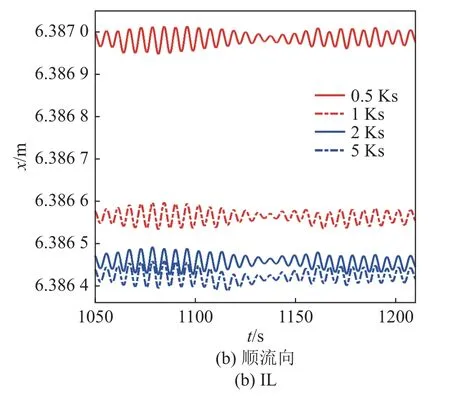
图17 不同土壤硬度下系统中点的横流及顺流向位移Fig.17 Displacement of system midpoint in the CF and IL directions with different soil hardness

图18 为不同土壤硬度下系统中点CF 及IL 方向的幅频曲线.由图可知,土壤硬度变化不会影响系统CF 及IL 方向的振动主导频率,但土壤硬度减小会增大系统振动的低频分量.由于土壤硬度变化产生的额外附加等效刚度较小,因此土壤硬度变化对系统中点CF 方向的振动幅值及振动频率影响较小.

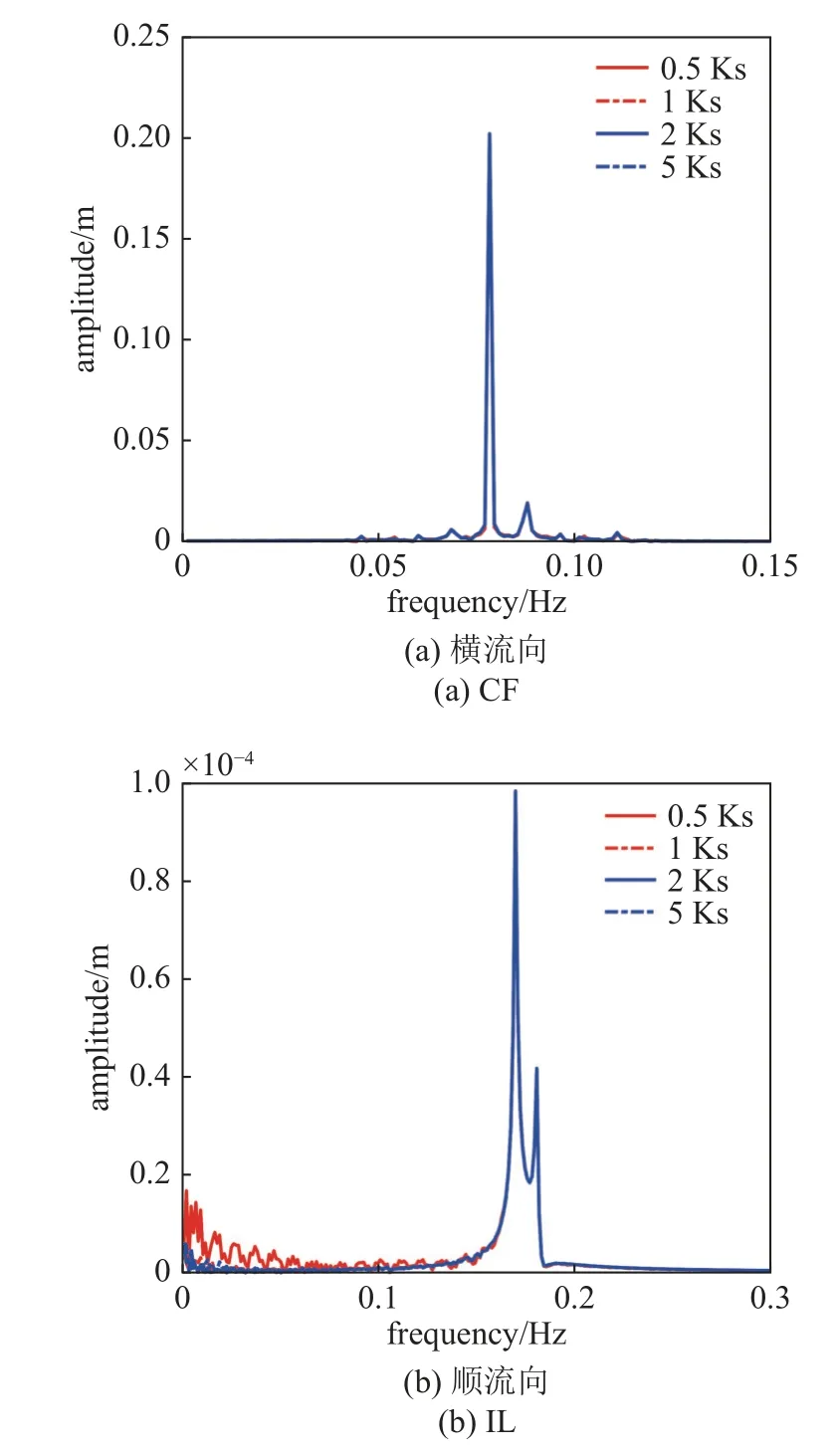
图18 不同土壤硬度下系统中点幅频曲线Fig.18 Amplitude-frequency curves of system midpoint with different soil hardness

图19 为不同土壤硬度下深水隔水管-水下井口系统CF 及IL 方向的弯矩.由图可知,土壤硬度变化对系统IL 方向的弯矩最大值影响较大,对系统CF 方向的弯矩最大值影响较小.系统CF 及IL 方向的弯矩最大值位置一直处于泥线以下,且最大值位置在系统刚度变化及非线性土壤抗力的综合影响下会随土壤硬度的增加而出现微小的浮动.

图19 不同土壤硬度下横流及顺流向弯矩Fig.19 Bending moment in the CF and IL directions with different soil hardness

4 结论

(1) 考虑管柱与土壤的非线性管-土耦合作用建立了深水隔水管-水下井口耦合系统双向VIV 三维分析模型.基于Newmark-β与4 阶龙格库塔法提出了深水隔水管-水下井口系统VIV 三维数值求解方法,验证了所建模型及分析方法的准确性.

(2) 通过所建模型及分析方法进行了管-土耦合下深水隔水管-水下井口系统VIV 分析,并与底部固支下深水隔水管-水下井口系统VIV 分析结果进行比较.对比结果表明,管-土耦合下的深水隔水管-水下井口系统CF 及IL 方向的RMS 位移及振幅增大,振动频率减小,系统最大弯矩点下移,最大弯矩明显提升.

(3) 研究了海流流速及土壤硬度对深水隔水管-水下井口系统VIV 的影响.系统VIV 对海流流速较为敏感,CF 及IL 方向的振动频率随海流流速增加而增大,与振动频率对应的模态振型也会随之改变.系统VIV 对土壤硬度的敏感性较低,原因是系统结构刚度与土壤初始附加的等效刚度较大,而土壤硬度变化额外附加的土壤等效刚度在系统总刚度中的占比较低.