固-液两相内流激励下悬臂输流管道稳定性特征研究1)
高 云 陈晓东 程 玮 刘 磊
* (哈尔滨工业大学(威海)海洋工程学院,山东威海 264209)
† (天津大学水利工程智能建设与运维全国重点实验室,天津 300072)
引言
输流管道在能源、海洋工程和化工等领域均有着非常广泛的应用.根据结构边界条件,输流管道可大致分为两类:一类是两端固支的输流管道;另一类是一端固支、另一端自由的悬臂输流管道.由于悬臂输流管道自由端与外界存在质量和动量交换,因此,与两端固支的输流管道相比,悬臂输流管道的动力学响应特征要更为复杂.为了保证流体能够在悬臂输流管道内进行安全、稳定地输送,有必要对悬臂输流管道的动力学响应特征展开深入研究.
根据管内介质不同,可以将悬臂输流管道动力响应特征研究划分为:单相内流激励下悬臂输流管道动力响应研究以及多相内流激励下悬臂输流管道动力响应研究.针对单相内流激励下悬臂输流管道的动力响应研究,目前已经取得了很多有意义的研究成果.Semler 等[1]基于哈密顿原理推导得到了二维悬臂输流管道动力学控制方程.Wadham 等[2]首先推导了三维悬臂输流管道的控制方程,同年,Wadham 等[3-4]分别对有弹簧约束的悬臂管道动力学和附加点质量的悬臂管道动力学[3]展开研究,发现理论结果与实验结果具有良好的一致性.Modarres等[5]研究了悬臂输流管道系统的颤振问题,主要探讨了质量比和重力参数的影响.包日东等[6]和Ghayesh等[7]研究了受约束的单相内流悬臂管道动力学特性,揭示了其通向混沌的途径.Yamashita 等[8]研究了受周期性激励的悬臂管道振动问题,对理论预测的激励效应进行了定性验证.Yun 等[9]提出了一种分析单相内流激励下悬臂管道自由振动的方法,得到了不同流速下的模态振型.王乙坤等[10]研究了悬臂管与松动约束的碰撞振动问题,得到了不同内流速度下摩擦力对管道动力学响应的影响规律.陶立佳等[11]研究了随从力作用下悬臂输流管道的稳定性,发现系统的失稳方式与临界流速大小有关.王乙坤等[12]研究了悬臂管道在内流激励下的参数共振行为,发现分布式运动约束力对管道位移响应有显著影响.易浩然等[13]研究了调控集中质量对悬臂输流管稳定性的影响,得到了集中质量位置对管道振幅表现的影响规律.Zhou 等[14]研究了基底激励下悬臂管道的振动响应特征,得到了在亚临界流速和超临界流速区间内管道的响应规律.方孟孟等[15]研究了悬臂输流管道在基础激励以及脉动内流联合作用下的动力学行为,发现相位差和频率比对系统的混沌百分比有重要影响.ElNajjar 等[16]研究了附加质量和弹簧位置对悬臂管道临界流速的影响,发现在特定位置添加附加质量和弹簧均可显著提高临界流速.2020 年开始,Chen 等[17-19]针对悬臂输流管道系统地开展了一系列研究工作,研究内容主要包括:重力作用下悬臂输流软管可能出现的极大幅度振动[17]、悬臂输流管道大变形振动的磁调控方法[18]以及三维悬臂输流管道的几何精确理论模型[19].近期,随岁寒等[20]研究了悬臂管道受重力和内流作用时的挠度和转角,发现随着内流流速增大,结构挠度和转角会减小.赵志贤等[21]研究了悬臂输流管道的自由振动问题,发现一端带有弹性支承的约束形式更有利于提高管道自由振动的稳定性.漆发辉等[22]研究了分布载荷作用下悬臂输流管道的稳定性,得到了分布载荷和质量比和黏弹性系数对系统失稳临界流速的影响规律.
相比于单相内流激励下悬臂输流管道,针对多相内流激励下悬臂输流管道动力响应的研究起步较晚,且研究成果也相对较少.Adegoke 等[23]研究了热载荷作用下输送两相流的悬臂管振动问题,发现温差、压力和顶部张力的增加会提高管道的横向振动频率.Liu 等[24]建立了输送气液两相段塞流的悬臂管道系统的动力学模型,分析了管道系统的固有频率.Ebrahimi 等[25]研究了不同两相流模型下悬臂管道结构的稳定性,发现模型的选择对失稳边界有显著影响,同时管道的动态响应在很大程度上取决于气体的体积分数.Guo 等[26]提出了考虑热效应的两相流悬臂式管中管系统自由振动的数学模型,发现管中管系统在稳定性方面优于单管输液系统.
由以上研究可以发现,目前针对内流激励下悬臂输流管道动力响应特征研究存在两个明显不足.(1) 目前绝大多数研究均是针对单相内流展开,而针对多相内流的研究较少.此外,在有限的针对多相内流的研究中,大多均是针对气-液两相内流展开,而针对固-液两相内流的研究则十分少见.(2) 在目前的研究中,绝大多数均假设管道质量分布具备均质特征,没有考虑附着在管道上的集中质量块引起的非均质特征.因此,端部带集中质量块的悬臂管道在固-液两相内流激励下的动力学响应特征、尤其是稳定性特征问题还有待深入研究.该研究对悬臂输流管道早期的合理设计、以及服役期的安全工作均有着重要的理论和工程价值.基于以上问题,本文基于能量法建立了固-液两相内流激励下带集中质量块悬臂管道的非线性耦合动力学模型,紧接着对管道动力学模型进行了数值求解,并对管道的稳定性特征展开了深入分析.
1 问题描述
如图1 所示,考虑一长度为L、外径为D、内径为d的悬臂输流管道在内流激励下的动力学响应特征问题,管道在自由端具有质量块me,管道内部介质为固-液两相流,流体流动方向自上而下,管道上端采用固接边界条件,下端采用自由边界条件.取管道顶端为原点o;z方向与管道未变形时轴线方向重合、且定义向下为正;x方向与管道振动方向重合、且定义向右为正;x和z两个坐标方向构成结构模型所在的二维坐标系.

图1 管道示意图Fig.1 Pipeline diagram
由于经典的Hamilton 原理不适用于本文所研究的悬臂输流管道模型,因此,这里将基于修正的Hamilton 原理建立管道振动方程.当管道自由端与外界存在质量与动量交换时,修正的哈密顿原理可表示如下[27]
式中,L 为系统拉格朗日函数,W为非保守力做功,M为管道内流质量,U为管道内流速度,rL为管道自由端位置向量,τL为管道自由端空间切向量.当仅考虑管道的平面内振动时,rL和τL可表示为rL=xi+zk,τL=x'i+z'k(其中′表示对管道z坐标求空间偏导).
值得注意的是,式(1)表示的是针对单相内流的修正Hamilton 原理表达式.若考虑固-液两相内流问题,式(1)可改写为
式中,Us和Ul分别为固相和液相的流动速度;Ms和Ml分别表示管道内部的固相质量以及液相质量.L=T-V,其中,T以及V分别表示振动系统的总动能和总势能.
当管道发生振动时,管内固体介质绝对流动速度vs以及管内液体绝对流动速度vl,可写作管道振动速度和管内介质对管道相对速度的关系表达式[28]
为了方便计算,这里没有对内部流场采用精细化建模,而是将内部流场看作是均匀定常流动.系统总动能T等于管道结构动能Tp、管内固体动能Ts以及管内液体动能Tl之和,表示如下
式中,mp是管道结构的质量.δ为Dirac 函数,单位为L-1,表示如下
系统总势能V等于管道内部固体重力势能、管道内部液体重力势能、管道结构重力势能、管道末端集中质量块me引起的重力势能、以及管道弯曲引起的弹性势能之和,可表示为
式中,κ=x″,为管道曲率.当忽略阻尼时,且不考虑系统外部的非保守力做功.通过系列变分操作及运算,可联立式(2)~式(6),得到如下动力学方程
假设固相和液相密度分别为ρs和ρl;固相和液相体积比分别为Qs和Ql(Qs+Ql=1);固相和液相的流动速度Us和Ul可通过滑移因子β建立联系,即Us=βUl.
当内部介质为固-液两相流时,式(7)中内流部分的质量项、动量项和动能项可表示成两相的叠加形式
联立式(7)和式(8),得到内部介质为固-液两相流时的结构振动控制方程
悬臂管道边界条件(上端固支、下端自由)可表示为
为方便描述结构动力学响应特征,需对方程(9)进行无量纲化,引入如下无量纲变量
式中,η为无量纲位移,ξ为无量纲坐标位置,τ为无量纲时间,整理得到如下无量纲方程
式中,各无量纲系数可表示为
其中,κ1为单位长度管道中无量纲液体质量,κ2为单位长度管道中无量纲固体质量,κ3为无量纲附加点质量,u为无量纲内部液相流速,χ为细长比,α为无量纲重力系数.无量纲形式的悬臂管道边界条件可写作
2 数值方法
对无量纲振动位移η进行Galerkin 离散,取前N阶模态振型,可写作
其中,ϕi(ξ)为悬臂边界条件下输流管道的第i阶模态振型,是第i阶广义坐标.对于悬臂结构,其模态振型可表示如下[28]
将式(15)代入式(12)后,再在方程左右两端同时乘以振型函数 ϕi(ξ),并在区间[0,1]上进行定积分,得到
式中,δ函数表示的附加点质量项的处理方式较为特殊[16],如下
将式(17)写作矩阵形式,表示为
将式(20)转化为一阶微分方程,可表示如下
式中
假设Z(τ)的表达式写为
将式(26)代入式(24)中得到
式中,I为单位矩阵,由式(27)可进一步得到
由式(28)可看出,λ为矩阵Y的特征值,对Y进行进一步展开,如下
特征值λ是一系列复数,特征值λ与特征频率ω之间存在恒定关系,即λ≡ iω[28].根据该关系式,基于矩阵Y的特征值λ便可非常方便地求解得到系统特征频率ω.特征频率的实部反应的是系统的固有频率,特征频率的虚部反应的是系统振动的稳定性特征.若存在特征频率虚部小于0 的情况,则认为结构发生失稳.
基于4 阶Houbolt 差分格式对方程(20)进行离散,随后采用Newton-Raphson 迭代法求解该线性方程组得到结构动力响应特征,该部分详细数值方法可参考Gao 等[29]的论文.
3 结果与讨论
3.1 理论及数值模型验证
为了验证本文中介绍的内流激励下输流管道稳定性特征分析理论及数值模型的可靠性,这里对其展开了验证.值得注意的是,对于带集中质量块的悬臂管道模型,由于缺乏管内为固液两相流的相关模型数据,这里仅对管内为单相流的模型进行验证.将本文中竖直方向的固液两相内流流动简化为水平方向的单相内流流动.针对水平方向的单相内流流动问题,可将式(7)进行退化并进行无量纲化处理,得到如下表达式
其中Mi为内部流动介质质量.基于第2 部分提出的理论及数值方法对式(30)进行数值求解,通过判断特征频率虚部得到管道发生颤振失稳时的临界速度uc.图2 给出了当μ=0.2,ξp=0.5 以及γ=0 时基于本文数值方法得到的临界速度uc与ElNajjar 等[16]研究结果的对比曲线.由图2 可看出:临界速度uc随β的变化趋势与ElNajjar 等的研究结果基本一致,从而验证了本文中判断内流激励下管道稳定性特征数值计算方法的可靠性.

图2 临界流速uc 验证图Fig.2 Verification diagram of critical velocity uc
这里,进一步对结构稳定性特征计算方法的可靠性展开了验证,基于前面的数值方法,分别对结构内流速度处于临界速度uc前的亚临界内流速度和临界速度uc后的超临界内流速度对应的结构动力学特征展开了分析.图3 分别给出了亚临界内流速度(ui=8.72)以及超临界内流速度(ui=8.73)对应的结构前4 阶模态振型对应的广义坐标.由图3 可以看出,当内流速度处于亚临界区间时,结构前4 阶模态振型对应的广义坐标时程曲线均呈现出随时间增加而逐渐衰减的特征,此时结构振动形式为衰减振动;当内流速度进入超临界区间时,广义坐标时程曲线均呈现出随时间增加而逐渐放大的特征,此时结构振动呈现出颤振失稳形式.

图3 内流速度区间内结构前4 阶模态广义坐标的时程振动曲线Fig.3 The time-history vibration curve of generalized coordinates of the first four modes of the structure in the supercritical internal flow velocity interval
3.2 结构稳定性特征分析
在本节稳定性分析中,分析模型所选取的相关参数与文献[30]保持一致,具体参数如表1 所示.
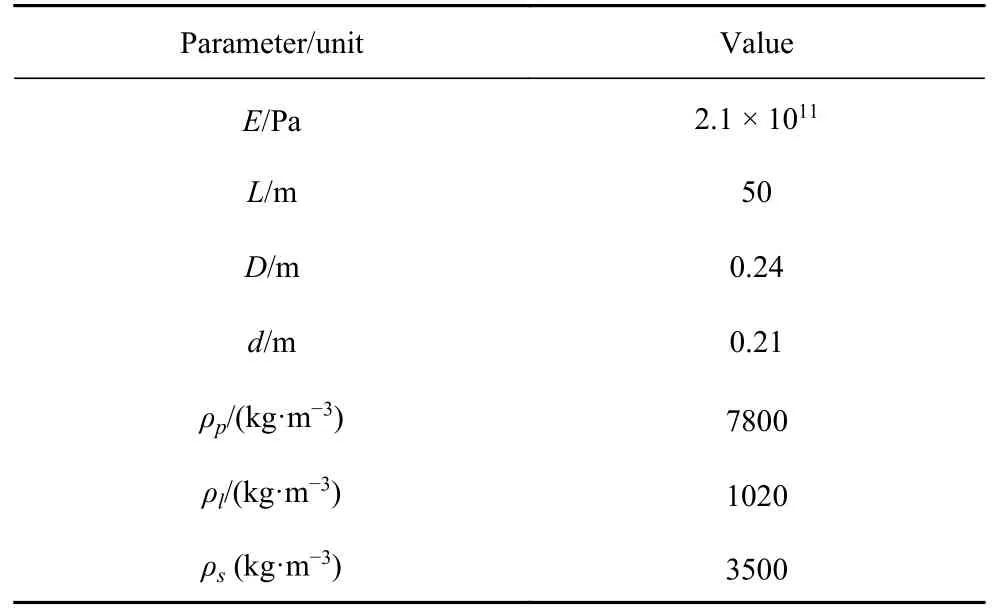
表1 悬臂管道基本参数Table 1 Basic parameters of the cantilevered pipe
这里首先系统地讨论了流致阻尼对系统稳定性的影响,研究了特征频率ω随无量纲内流速度ui的变化特征.研究过程中,无量纲端部质量ĸ3=1.0×10-4,无量纲固相比Qs=0.5.图4 给出了管道复频率随内流速度变化的Argand 图.由图4 可以看出:当无量纲内流速度ui较低(ui<20.9)时,所有模态的特征频率虚部Im(ω)均为正数,意味着系统无法从内部流体中获得能量,此时,管道振动呈衰减特征,结构振幅随时间变化逐渐趋于0.随着ui的增加,当ui增加至临界速度20.9 时,第3 阶模态特征频率虚部Im(ω)首先从正值跨过0 点变为负值,对应的结构阻尼比ζ=Im(ω)/Re(ω) <0,由结构动力学可以知道,结构阻尼比ζ=c/2mωn,所以此时的流致阻尼为负数,意味着系统将从内部流体中获得能量,此时,结构发生颤振失稳,振幅将趋于无穷大.
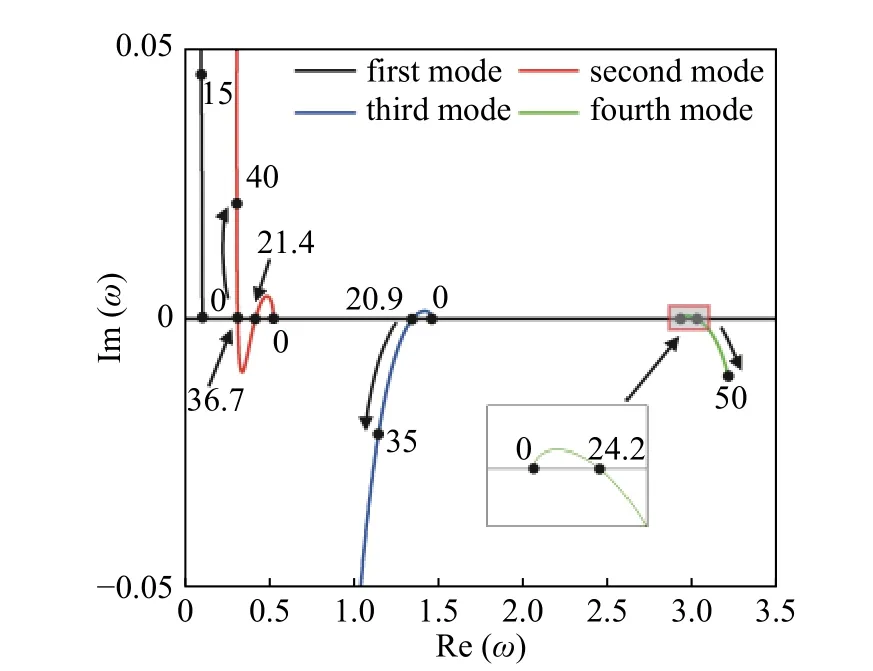
图4 管道特征频率随内流速度变化特性Fig.4 Characteristic frequency of pipeline varied with internal flow velocity
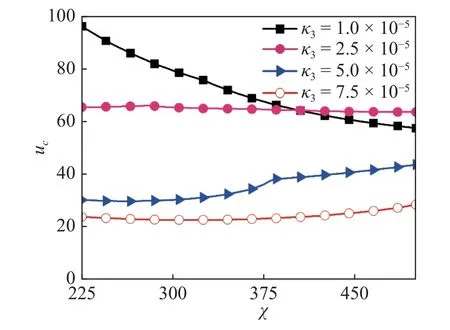
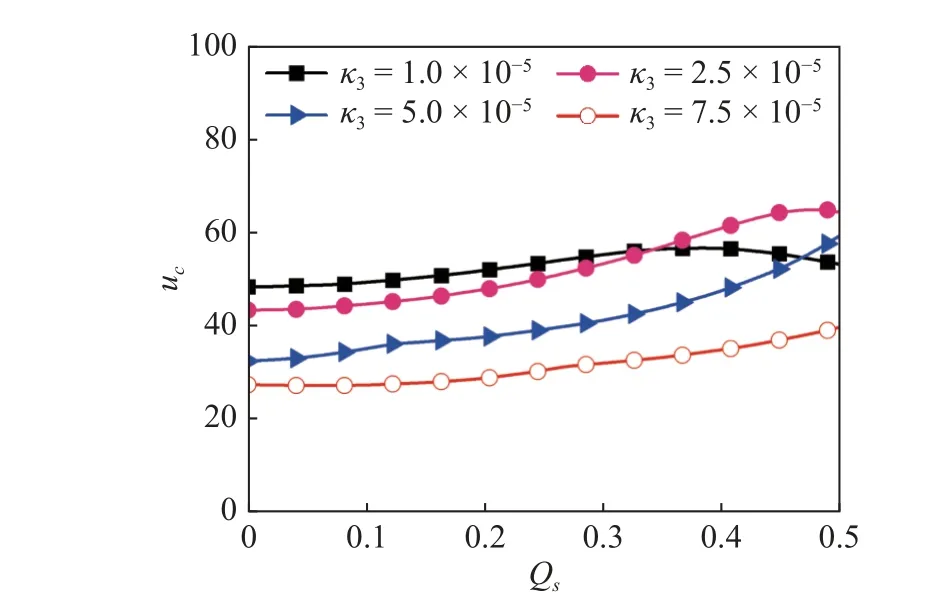
为了进一步研究流致阻尼对系统稳定性的影响,同时验证图4 给出的不稳定性的定性判断结果,这里计算了临界流速uc前和达到临界流速uc时这两种内流速度(ui=20.8,20.9)对应的广义模态坐标随时间变化的特征(如图5 所示).由图5 可看出,当ui 图5 广义模态坐标振动时程曲线Fig.5 Generalized modal coordinate vibration time history curve 图6 给出了4 种不同的无量纲端部质量块ĸ3下系统临界流速uc与细长比χ的变化关系图.由图6可以看出,针对不同的ĸ3,临界速度uc随细长比χ的增加呈现出不同的变化特征.当ĸ3较小(ĸ3=1.0×10-5)时,随着χ的增大,uc呈下降趋势,说明此时端部质量块质量对结构刚度的影响较小,结构的柔性增加导致了结构的不稳定性增加.随着ĸ3的增加,当ĸ3取较大值(ĸ3=2.5×10-5)时,随着χ的增大,uc几乎保持不变.当ĸ3进一步增加到5.0×10-5和7.5×10-5时,随着χ的增大,uc呈现先保持不变、后缓慢增大的趋势. 图6 不同长细比χ 对应的失稳临界速度Fig.6 Critical velocity at different aspect ratios,χ 图7 给出了4 种不同的无量纲端部质量块ĸ3下系统临界流速uc与管道重力系数α的变化关系图.由图7 可以看出,当ĸ3较小(ĸ3=1.0×10-5)时,uc随着α的增大而迅速减小,随着α的不断增大,uc变化减缓,但总体变化趋势不变.相比细长比χ,管道重力系数α对临界速度的影响要复杂很多.随着ĸ3的增加,当ĸ3较大(ĸ3=2.5×10-5)时,随着α的增大,uc缓慢减小.当ĸ3进一步增加到5.0×10-5和7.5×10-5时,随着α的不断增大,uc总体呈增大的趋势. 图7 不同重力系数α 对应的失稳临界速度Fig.7 Critical velocity at different gravity coefficients,α 从4 条曲线变化趋势可以看出,当重力系数α达到最大值(α=1.0×10-5)时,4 条曲线终点不断趋近,此时uc大小接近相等.这说明,随着α的不断增大,ĸ3对uc的影响不断减小. 图8 给出了4 种不同端部质量块ĸ3下系统临界流速uc与管道固相比Qs的变化关系图.当ĸ3较小(ĸ3=1.0×10-5)时,随着Qs的增大,uc不断增大,当Qs增大到0.4 左右,uc增大到最大值,接着随着Qs的不断增大,uc不断减小.随着ĸ3的增加,当ĸ3较大(ĸ3=2.5×10-5)时,随着Qs的增大,uc先不断增大,接着有减小的趋势,uc达到最大值对应的Qs大于0.4,出现最大值后移现象.当ĸ3进一步增加到5.0×10-5和7.5×10-5时,随着Qs的增大,uc呈现出不断增加的趋势. 图8 不同固相比Qs 对应的失稳的临界速度Fig.8 Critical velocity at different solid phases,Qs 本文利用能量法建立了带集中质量块的悬臂输流管道的结构动力学方程,使用4 阶Galerkin 法对结构方程进行了时空离散,得到了常微分方程组.随后,将常微分方程组写成矩阵形式,并基于特征值法对管道的稳定性特征进行了研究.本文针对端部质量块ĸ3、细长比χ、重力系数α和固相体积比Qs对临界流速uc的影响展开了深入分析.基于以上分析结果,得到结论如下. (1)当内流速度处于亚临界区间时,系统特征频率虚部均为正数,结构无法从流体中获取能量,结构振动形式表现为衰减振动;当内流速度处于超临界区间时,系统的某阶特征频率虚部会出现负数,结构会从流体中持续不断地获取能量,结构振动形式表现为颤振失稳. (2)当重力系数较小时,临界速度受端部集中质量块的影响非常明显,且随着端部集中质量块质量的增加呈下降趋势;随着重力系数的增加,端部集中质量块对临界速度的影响逐渐降低.当质量系数增加到1.0×10-5时,不同端部集中质量块下的临界速度基本保持不变. (3)当细长比和固相比较小时,临界速度随着端部集中质量块质量的增加均呈下降趋势;当细长比和固相比较大时,临界速度不再随着端部集中质量块的增加呈单调变化趋势,而是呈现出较为复杂的变化趋势.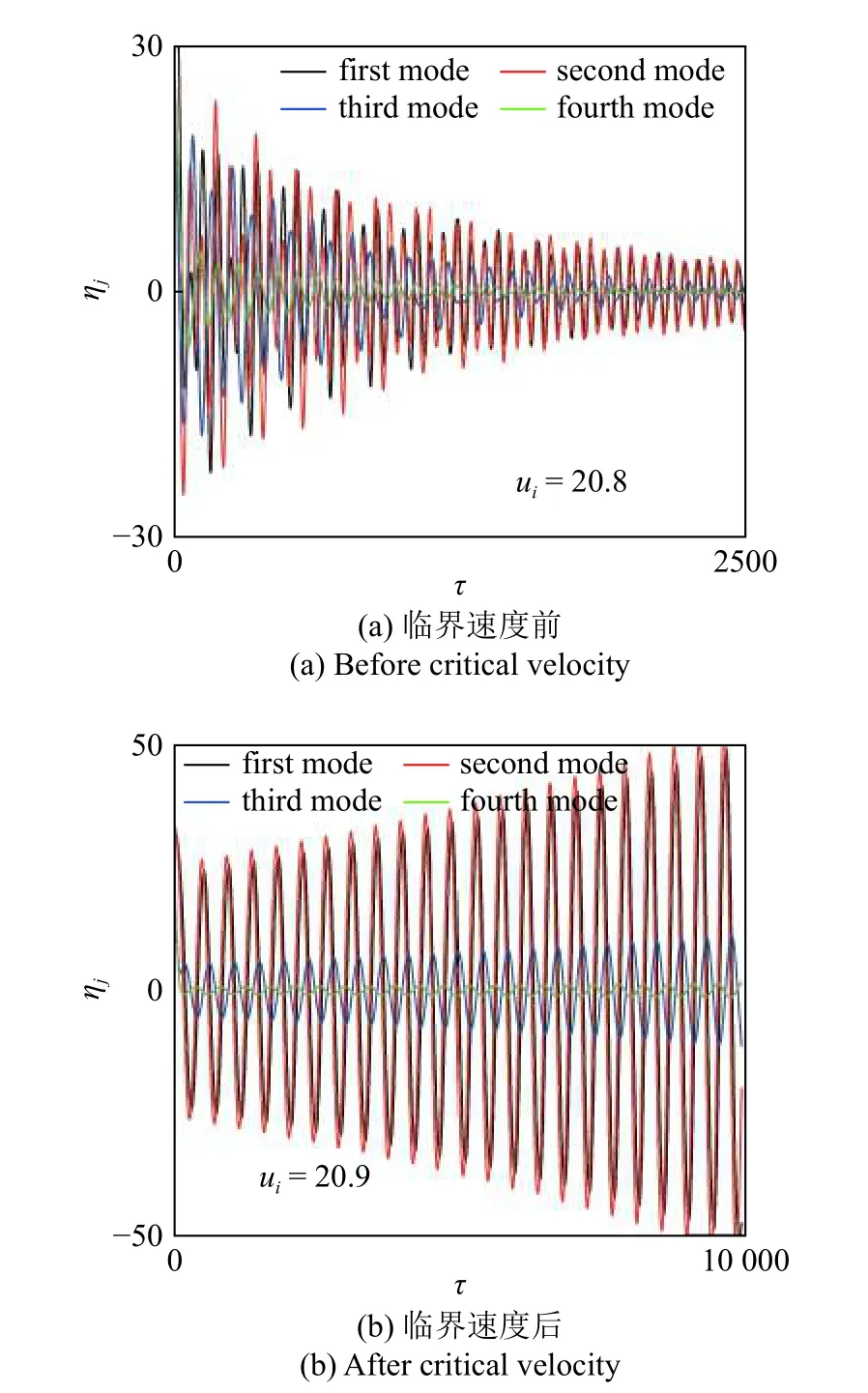

4 结论

