一种新的内翻管理论模型及其耐撞性研究1)
张婉琪 尹冠生 ,†, 姚如洋 史明辉 韦鹏飞 王建强
* (长安大学理学院,西安 710064)
† (西安汽车职业大学交通工程学院,西安 710600)
** (湖南大学整车先进设计制造技术全国重点实验室,长沙 410082)
†† (西安中交土木科技有限公司,西安 710075)
引言
金属薄壁圆管作为吸能元件具有质量轻、成本低、吸能效率高等优点,在汽车[1-2]、飞行器[3]、轨道交通[4-5]和船舶[6]等领域有着广泛应用.理想的吸能元件总是追求更平稳的载荷和更大的吸能量.圆管直接承受轴向载荷时的渐进屈曲模式不仅有过大的初始峰值载荷且后续载荷波动较大[7-9],这都不利于吸能元件保护主体结构或者乘客的安全.因此,学者们尝试了不同的方法改变圆管自身以降低初始峰值载荷并使压缩力均匀化,例如开孔[10]、刻槽[11-12]和波纹[13]等.此外,还可以通过管端的不同模具将圆管变形模式从渐进屈曲改变为膨胀[14]、收缩[15]、撕裂[16]和翻转[17]等以改善其耐撞性.其中翻转模式由于没有初始峰值载荷且成功翻转后载荷稳定[18]等优点在航空航天和汽车工程的吸能器设计中得到广泛应用[19].
翻转模式根据翻转方向的不同分为外翻模式和内翻模式.其中外翻模式更易实现,所以关于圆管圆角模具外翻的研究较多[20-25].外翻模式理论研究多基于曲率不变的几何模型[20-22].然而大量试验和有限元结果均显示外翻过程的变形区曲率是变化的[22].Leu[23]提出了曲率在与模具分离的瞬间改变的外翻几何模型,即变形区由两个曲率不同的1/4 圆组成,但并未给出曲率改变后变形区曲率的理论解.Yu等[24]采用上述几何模型对外翻过程进行了理论研究,得到了曲率突变后的成形半径理论值.相较传统曲率不变几何模型提高了理论预测精度,但研究过程忽略了分离点的曲率突变,因此得到的稳态力理论结果仍与试验结果存在误差.基于此,本文作者[25]提出了一种新的圆管圆角模外翻几何模型,该几何模型假设翻转变形区曲率连续变化且得到的成形半径更接近试验结果.基于上述外翻几何模型的研究结果和已有内翻模式试验结果[26-27],不难得到内翻过程的变形区曲率也是变化的.然而以往关于内翻模式的理论研究都基于曲率不变的几何模型[28-31].
与外翻模式不同的是,内翻模式几何模型除了考虑曲率变化,还应同时考虑壁厚增厚效应.试验结果[22]得到外翻管壁变薄,但其变薄效应可忽略;内翻管壁变厚,其增厚效应不可忽略.Reid 等[26]和Rosa 等[27]根据试验结果得到管内翻后的壁厚约为初始壁厚的1.5 倍,但并未给出成形壁厚的理论值.罗云华等[28]和牛卫中[29-30]根据曲率不变的几何模型得到了成形壁厚表达式.但由于壁厚增厚效应与周向收缩程度密切相关,而曲率不变的几何模型不能准确预测周向收缩程度,因此上述模型得到的成形壁厚理论值仍与试验结果误差较大.且文献[29]中的成形壁厚理论值需多次迭代得到.
另外现有关于翻转模式的研究多只针对稳态力[24,28-29],关于翻转全过程力位移关系的研究较少.但是除了稳态力,总吸能和比吸能也是翻转管作为吸能元件的重要耐撞性指标.而只有得到全过程力位移曲线才能得到总吸能和比吸能的理论结果.Miscow 等[20]通过能量法得到了外翻全过程翻转力表达式,但其存在一个与试验结果不符的高于稳态力的初始峰值载荷.Niknejad 等[21]将外翻过程分为3 个阶段,根据能量法得到外翻全过程翻转力.由于在外翻稳态力的计算中考虑了管端的收缩应变,所以该理论模型预测的稳态翻转力偏大.关于内翻过程,仅有Rajabiehfard 等[31]将动态冲击条件下内翻过程分为4 个阶段得到全过程翻转力,而未有关于准静态内翻全过程的理论研究.上述对于外翻或者内翻的理论研究均独立进行,没有关于两种翻转模式的统一研究且计算过程复杂.本文作者[25]将外翻过程简化为两个阶段进行理论分析,根据能量法得到了外翻全过程的力位移曲线,并经试验结果验证了理论模型.
本文针对圆管圆角模具内翻模式进行研究,通过试验和有限元模拟得到内翻变形模式特点及其与外翻变形模式的几何联系.基于以上结果,提出新的同时考虑变形区曲率变化和管壁增厚效应的内翻模式几何模型.通过该几何模型得到了内翻成形壁厚、临界位移和最大位移等几何参数.基于该几何模型和能量法得到了内翻稳态力和全过程力位移关系,进而得到总吸能和比吸能等吸能指标.经试验和有限元结果验证了上述理论结果的正确性.最后通过内翻理论模型对吸能指标进行参数分析,为内翻管作为吸能元件的应用提供了理论依据.
1 翻转试验及有限元建模
1.1 问题描述
当长度为L,壁厚为t0,平均半径为R0的圆管上端受到载荷P的作用时,管下端沿着圆角半径为r的模具变形.管端向内翻转为内翻模式,如图1(a);管端向外翻转为外翻模式,如图1(b).对于两种翻转模式,A,B,C3 点有着相同的定义:其中A点为管下端初始位置,也是变形区起点;B点为圆管离开模具的位置,即变形由模具限制变为自由卷曲;C点为变形区终点.定义A点的曲率半径为弯曲半径rAi(rAe),C点半径为成形半径rCi(rCe),翻转后行成的双壁管的内外壁周向半径差为最大半径差 ∆Rmaxi(∆Rmaxe)(对于内翻过程,最大半径差为初始外壁与翻转后内壁的周向半径差;对于外翻过程,最大半径差为初始内壁与翻转后外壁的周向半径差),下标i 和e 分别代表内翻模式和外翻模式.另外定义内翻过程C点壁厚为成形壁厚tCi.

图1 圆角模具翻转过程示意图Fig.1 Axial profile for inversion process over a circular die
对于图1 所示的两种翻转模式,成形半径均是决定变形模式以及计算稳态力等吸能指标的关键.文献[25]给出外翻成形半径rCe的理论公式,并经试验结果进行了验证.内翻模式的成形半径及全过程变形模式特点需要试验和数值模拟进一步得到.本节针对以上问题进行了试验和有限元模拟设计.
1.2 翻转试验
本文选用图2 所示A (R0=19.5 mm,t0=1 mm),C (R0=33.4 mm,t0=1.2 mm)两种尺寸的商用无缝6063 铝管进行翻转试验,试件高度L均为100 mm.底端模具采用不锈钢材料加工.准静态轴压翻转试验在CMT535 试验机上进行,如图3.为保证试验处于准静态,加载速度采用2 mm/min.为保证圆管顺利翻转,采用润滑油和石墨粉混合作为润滑剂.当圆管下端经翻转接触到上板时,停止加载,记录此刻的位移为翻转最大位移xmaxi(xmaxe) .工况命名的首字母代表圆管类型,中间两位代表模具半径,后两位代表翻转方向,例如Ar3IN 代表A 管在圆角半径为3 的模具上内翻工况类型如表1 所示.试验完成后,沿着中轴线切割样本,以便测量最大半径差和内翻成形壁厚.
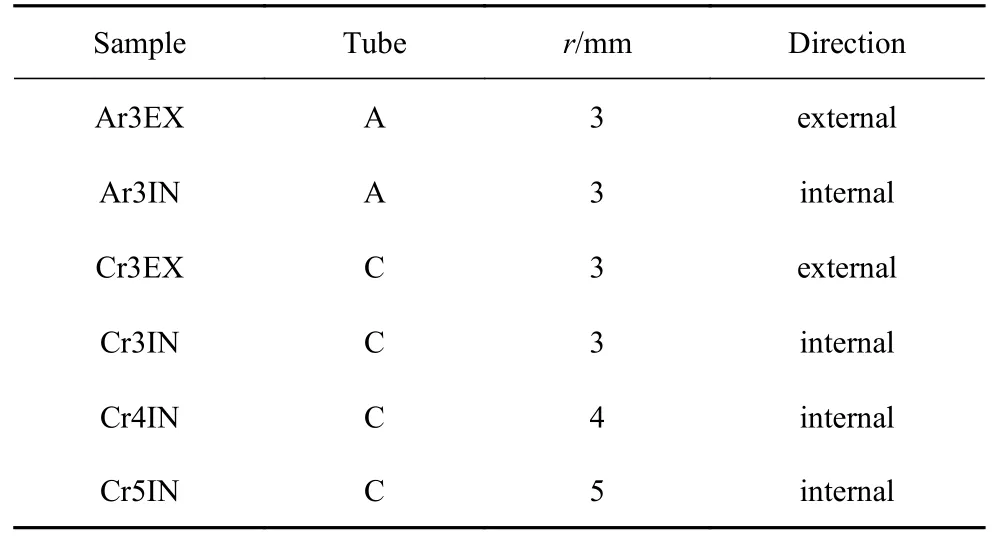
表1 设计工况Table 1 Design conditions

图2 6063 铝管及不锈钢模具Fig.2 6063 aluminum tubes and stainless steel die

图3 试验装置Fig.3 Schematic of test setup
为确保后续有限元和理论分析的准确性,对A 和C 两种圆管材料分别测定其材料参数.根据ASTME8 标准分别从两种管件轴向切割出3 个弧形截面的拉伸试样,其尺寸如图4 所示.单轴拉伸试验在UTM6503 试验机上进行,加载速度为2 mm/min.各管的工程应力应变曲线如图5.表2 给出两种铝管的材料参数.
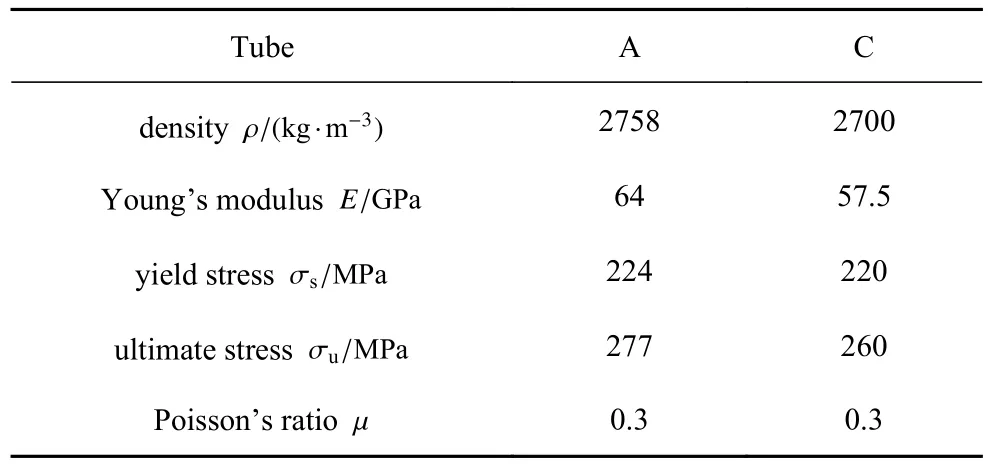
表2 铝管材料参数Table 2 Material properties of the aluminum tubes
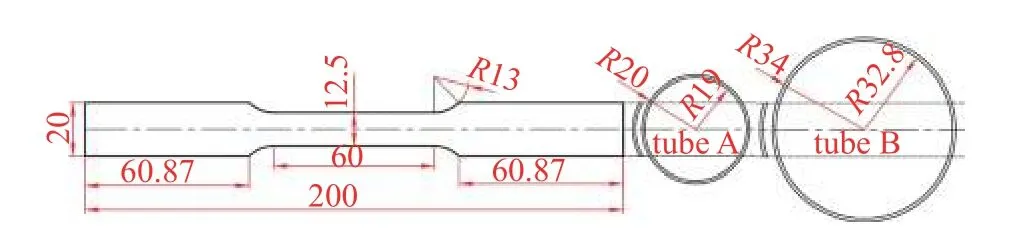
图4 拉伸试件尺寸(单位:mm)Fig.4 The dimentions of tensile speciments (unit:mm)
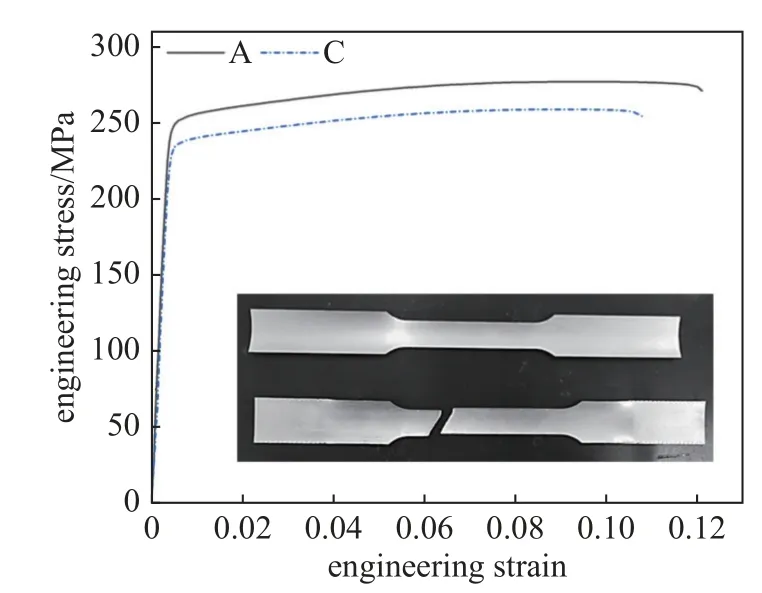
图5 6063 铝管的工程应力-应变曲线Fig.5 The engineering stress-strain curves of 6063 aliminiun tubes
1.3 有限元建模
为了更好地分析内翻全过程的变形模式并分析更多的工况以节约试验成本,借助有限元软件ABAQUS对圆管圆角模具翻转过程进行数值模拟.由于整个翻转过程中圆管的几何形状和边界条件均关于圆管中轴线对称,所以采用轴对称模型进行数值模拟以降低计算成本.假定平板和模具为刚体,选用2 节点线性轴对称离散刚体单元RAX2 对两者进行网格划分.圆管选用4 节点轴对称单元CAX4R 进行网格划分.将1.2 节中试验得到的工程应力应变曲线转化为真实应力应变曲线并用于数值模拟.由于铝合金在低速压缩时通常表现出较低的应变率敏感性,因此可以忽略应变率效应[32-33].对底部圆角模具的所有自由度均进行约束,而上部平板仅沿轴向的位移不受约束.按照平滑幅值曲线给上板施加70 mm 轴向位移,加载时间为0.07 s.此速度下动能远低于总能量的5%,所有变形过程可视为准静态[34].分别设置圆管所有表面与平板下表面和模具上表面为面面接触以模拟实际翻转过程中圆管与上板和模具的接触.设置圆管自身所有表面自接触以模拟管端与管壁可能发生的干涉或屈曲失稳时管壁自身的接触.文献[25]详细讨论了摩擦系数对外翻模式数值结果的影响,结果表明摩擦系数对于外翻模式的成形半径等几何参数影响不大;摩擦系数越大,翻转力越大.当摩擦系数取0.15 时,数值结果、试验结果和理论结果三者均吻合得很好.对于内翻工况Ar3IN 设置不同摩擦系数进行有限元计算,结果显示与外翻模式相同,摩擦系数仅对翻转力有较为明显的影响,对于成形半径和成形壁厚等几何参数的影响可忽略.对比还发现同样在摩擦系数设置为0.15 时,翻转力的数值结果与试验结果吻合.故本文对于内翻模式的数值模型同样取摩擦系数为0.15 进行计算.
1.4 试验结果与有限元结果的分析
图6(a)和图7(a)分别给出内翻工况Ar3IN 和外翻工况Ar3EX 的全过程力位移曲线.如图所示,两个工况数值模拟得到的力位移曲线均与试验结果吻合得很好,这说明数值模型关于摩擦力的取值是正确的.图6(b)和图7(b)分别给出内翻模式和外翻模式力位移曲线上4 个典型时刻对应的变形模式.其中 Ⅰ 时刻对应第一个局部峰值力,此刻管下端与模具存在最大间隙.随着管壁逐渐贴紧模具,翻转力下降达到 Ⅱ 时刻对应的局部峰谷力.Ⅲ 时刻后翻转力趋于平稳,此刻管端大约翻转了270°,且管端形状明显不是3/4 圆,各点曲率明显变化.Ⅳ 时刻为翻转结束时刻,管端接触上板,可观察到内翻后的内壁明显增厚.

图7 Ar3EX 工况的力位移曲线与变形模式Fig.7 The force displacement curves and the deformation mode for sample Ar3EX
以往关于翻转全过程的研究,均将Ⅲ 时刻之前的翻转过程细分为多个阶段进行分析.但根据翻转模式力位移曲线所呈现出的特点,Ⅲ 时刻之前的翻转力总体随着位移的增大而增大,虽然存在若干局部峰值力,但其对于翻转力的变化趋势影响不大,且对于力位移曲线在横坐标轴上的投影面积影响不大,即对于翻转模式总吸能的影响很小.因此在后续理论分析中忽略Ⅲ 时刻之前的翻转力波动.
根据上述关于翻转模式力位移曲线及典型时刻变形模式的讨论,将内翻过程和外翻过程都简化为两个阶段:弯曲阶段和稳定阶段.Ⅲ 时刻为两个阶段的分界点,定义Ⅲ 时刻为临界时刻,此刻的位移为临界位移xmi(xme) .Ⅳ 时刻为最终时刻,此刻位移为最大位移xmaxi(xmaxe) .稳定阶段的翻转力为稳态力Pmi(Pme) .
图8 给出4 种内翻工况最终时刻管件剖面的试验与有限元结果,可以得到两者变形模式吻合较好.表3 给出各工况最大半径差,成形壁厚以及最大位移等几何参数和稳态力的试验与有限元结果.根据表3 可进一步得到有限元模拟可以很好地预测试验得到的变形模式与稳态力.另外分析表3 中各工况的最大半径差,可近似认为同尺寸圆管在相同模具半径下内翻和外翻的最大半径差相同

表3 最大半径差、成形厚度、稳态力和最大位移的试验结果和数值结果对比Table 3 Comparisons of the experimental and simulation results for the maximum radius difference,the forming thickness,the steady inversion force and the maximun displacement

图8 内翻过程变形模式的试验与数值结果Fig.8 The deformation modes of experiment and numerical results for internal inversion process
2 圆管圆角模具内翻理论模型
为了简化分析过程,对圆管内翻过程采取如下假设.
(1)由于管件几何形状、模具几何形状以及管件受力大小方向均关于圆管轴线轴对称,则内翻过程中圆管的变形为轴对称变形.
(2) 内翻过程中AB段圆管与模具始终完全贴合,管件长度无变化.
(3)仅考虑管件能稳定内翻的工况.不考虑由于圆管尺寸、初始缺陷和模具尺寸等原因造成的失效模式.
(4)忽略弹性变形,仅考虑翻转过程中的塑性大变形.即假设圆管材料不存在包辛格效应,为各向同性的理想刚塑性材料.材料流动应力取屈服应力与极限应力的平均值[7]
其中,σ0为流动应力,σs为屈服应力,σu为极限应力.
(5) El-Domiaty[35]通过理论分析得到外翻过程中子午线方向弯曲应变和周向拉伸应变约为其他应变分量的20 倍,所以在用能量法求解外翻稳态力时其他应变可忽略不计.本文作者[25]在采用能量法分析外翻过程时,同样只考虑了子午线方向弯曲耗能和周向拉伸耗能,摩擦耗能在修正模型中单独考虑.因此对于内翻过程,同样仅考虑子午线方向弯曲耗能和周向收缩耗能,而未考虑径向曲率变化和轴向压缩等变形引起的塑性耗能.假设外力做功完全由塑性变形耗散,即
(6)假设弯曲阶段的翻转力与位移为二次函数关系;稳定阶段的翻转力维持内翻稳态力恒定不变.则根据内翻临界位移、内翻最大位移以及内翻稳态力即可得到内翻全过程力位移曲线的理论结果
2.1 成形半径、成形壁厚、临界位移和最大位移
由图1 和图9 可知,内翻弯曲半径rAi与外翻弯曲半径rAe相同,仅与模具半径和圆管初始壁厚相关
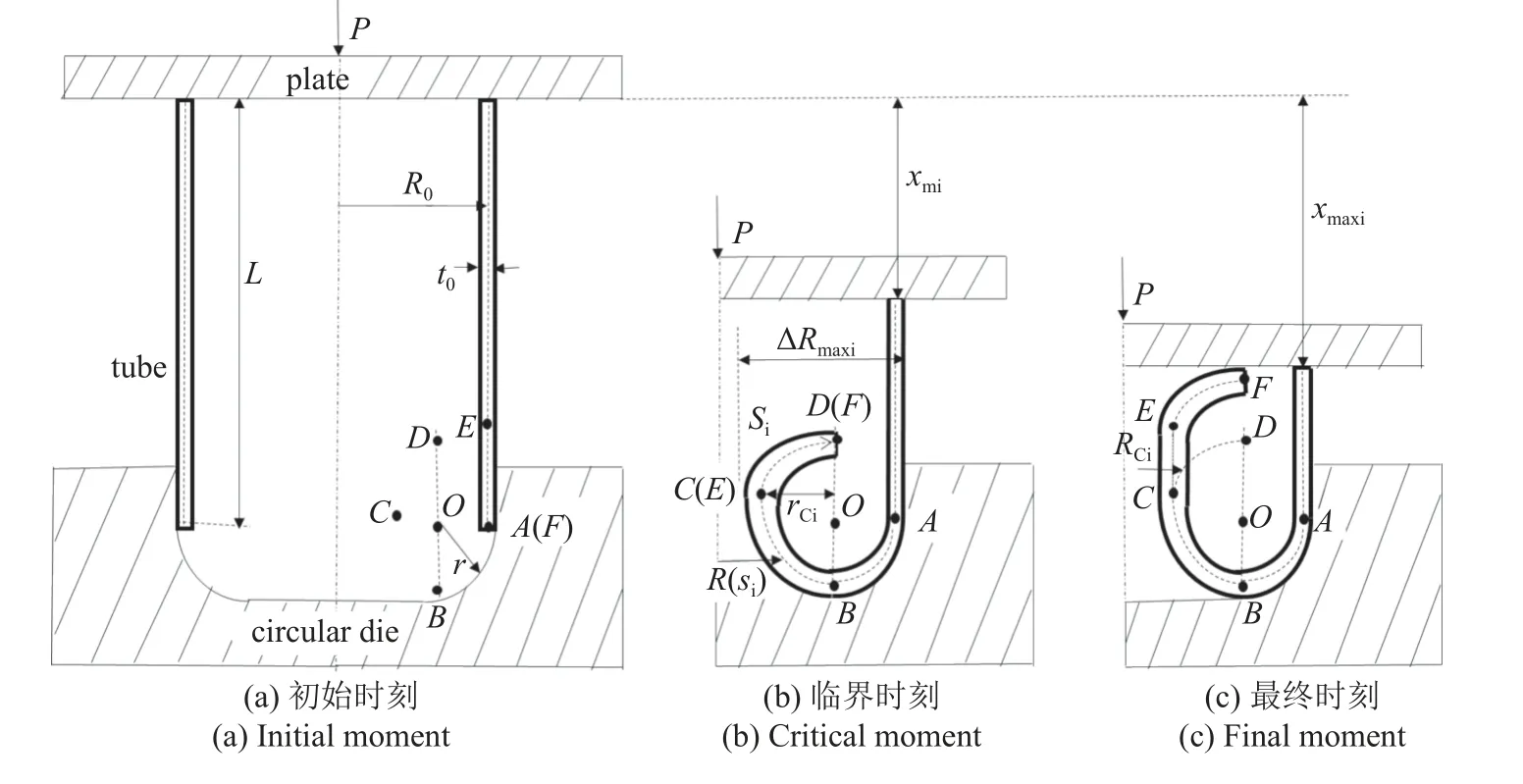
图9 圆管圆角模内翻几何模型Fig.9 Axial profile of geometrical model of an internal inversion process over a circular die
即内翻A点曲率为 κAi=κAe=1/rAe.
由图9 可得B点的周向半径,即B点距圆管中轴线的距离为
根据B点壁厚和模具半径得B点曲率半径
则B点曲率为 κBi=1/rBi.
在1.4 节中根据试验和有限元结果得到,同尺寸圆管在相同模具半径下内翻和外翻的最大半径差相同,又根据材料守恒有
其中RCi为内翻过程C点的周向半径.由图1 得到如下几何关系
将式(10)代入式(1)和式(9)并联立两式得到内翻过程的成形半径rCi和成形壁厚tCi
其中,m=R0-r+rCe+t0,n=rCeR0-rrCe+0.5t0rCe+0.5t0r+0.25t02.
由于不考虑管件长度变化,因此内翻临界位移等于圆管下端F依次经过A,B,C,D4 点的位移.假设AB,BC和CD各弧段两端切线夹角均为,则各段弧长近似为
因此,内翻过程的临界位移为
根据图9 所示几何关系得到内翻模式最大位移
2.2 内翻稳态力
2.2.1 子午线方向弯曲耗能
如图9(c)所示,内翻稳定阶段子午线方向曲率在A点和C点发生突变,在AB段内和BC段内分别连续变化,B点无曲率突变.因此内翻模式稳定阶段的子午线耗能应包含4 部分:A点曲率突变引起的弯曲耗能;C点曲率突变引起的弯曲耗能;AB段内曲率变化引起的弯曲耗能以及BC段内曲率变化引起的弯曲耗能.
A点子午线方向曲率由0 突变为 κAi,则A点曲率突变所引起的子午线方向弯曲耗能为
同理C点曲率突变所引起的子午线方向弯曲耗能为
假设AB段曲率逐渐变大且呈线性分布,则AB段各点曲率与坐标si的关系为
因此,AB段内子午线方向弯曲耗能为
同理,BC段各点曲率与坐标si的关系为
因此,BC段子午线方向弯曲耗能为
则单位时间内圆管子午线方向弯曲耗能为
2.2.2 周向收缩耗能
在变形区ABC的翻转过程中,任一点距圆管中心轴的距离为R(si),其中A点的周向半径为R0,C点的周向半径为Rci,则单位时间内变形区周向收缩所引起的压缩应变
根据压缩应变得单位时间圆管周向压缩耗能
将式(29)和式(31)代入式(3)得到不考虑摩擦效应的内翻稳态力
2.3 考虑摩擦效应的修正模型及吸能指标
为了简化计算,在上述分析中没有考虑圆管与模具之间的摩擦效应.但是在翻转过程中,特别是在内翻过程中,圆管与模具之间的摩擦耗能也会对翻转模式产生较大的影响.甚至当摩擦力较大时,摩擦效应会影响圆管能否成功翻转.在外翻理论模型中假设摩擦耗能独立于塑性耗能,得到考虑摩擦效应的修正外翻稳态力[25]
其中Pme为外翻稳态力,Pmef为修正外翻稳态力,f为圆管和模具接触面摩擦系数.当摩擦系数取0.15 时,数值结果和理论结果均符合试验结果[25].这与文献[37]中提到的用矿物油做润滑剂时,摩擦系数取0.15~0.16 符合.
在圆管内翻过程中,同样假设摩擦耗能独立于塑性耗能[25,34],参照式(31),得到考虑摩擦效应的修正内翻稳态力
其中,f为圆管和模具接触面的摩擦系数.已在本文1.4 节中得到,当摩擦系数取0.15 时,内翻稳态力的数值结果与试验结果符合.因此在后续理论模型与试验结果对比验证时,仍然采用摩擦系数为0.15.
用式(32)的修正内翻稳态力替换式(4)中的内翻稳态力即可得到修正的内翻过程力位移曲线
对上式积分得内翻过程总吸能
比吸能经常用来量化单位质量材料的吸能能力
其中,M为管件的总质量.
3 结果与讨论
3.1 力位移曲线的验证
内翻模式力位移曲线的理论结果由式(33) 得到,其中摩擦系数取0.15.罗云华等[28]根据平衡法得到的内翻稳态力理论结果为 (Pmi)L.4 种内翻工况力位移曲线的试验、数值和理论结果如图10.结果显示,本文理论公式得到的力位移曲线与试验和数值结果均吻合较好.而文献[28]得到的稳态力均远低于本文试验和数值结果.在弯曲阶段,试验和数值结果均存在局部峰值力且两者吻合较好.出现局部峰值力的原因已在1.4 节中讨论.
本文的力位移曲线理论结果由临界位移,最大位移和内翻稳态力决定,表4 给出三者的理论值与数值结果的对比.结果显示,临界位移理论结果与数值结果的最大误差为5.83%;最大位移的最大误差为0.66%;内翻稳态力的最大误差为6.47%.其中内翻稳态力的误差相对较大,且理论结果均小于数值结果和试验结果.其中一个主要原因是内翻过程中圆管轴向受的压缩作用在理论模型中并未考虑.

表4 临界位移、最大位移和稳态力的理论值与数值结果对比Table 4 Comparisons of the theoretical predictions with simulation results for critical displacement,maximum displacement and steady force
Rosa 等[27]在准静态条件下对平均半径为19.5 mm,壁厚为1 mm 的6060 铝管在圆角半径为4 mm 的模具上进行了内翻试验.润滑剂采用聚四氟乙烯,摩擦系数取0.05.试验得到该工况的稳态内翻力为23.5 kN.本文理论模型得到的内翻稳态力为24.1 kN,与试验结果误差为2.5%.其力位移曲线的试验结果与本文理论得到结果如图11 所示,结果显示本文理论结果与Rosa 等[27]试验结果吻合.
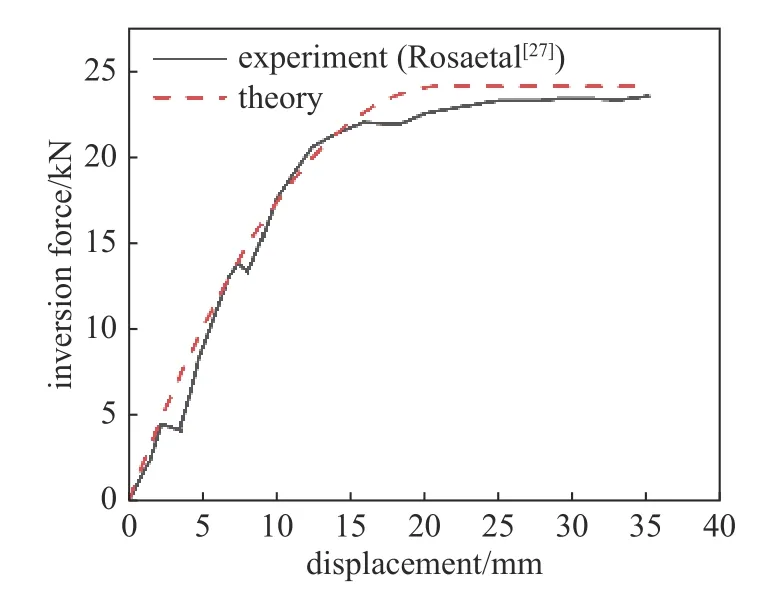
图11 本文理论结果与Rosa et al.[27]试验结果的对比Fig.11 Comparisons of the theoretical predictions with experiment results of Rosa et al.[27]
3.2 变形模式的验证与讨论
对于变形模式的合理假设是得到正确力位移曲线的基础.3.1 节对于特定工况力位移曲线的验证可以反向初步说明本文理论模型中对于变形模式诸多假设的合理性.本节对变形模式进行讨论验证以进一步说明本文理论模型的合理性.图12 给出内翻模式稳态阶段变形区示意图,为了更清楚地展示管壁的变化,图中放大了壁厚增厚效应.

图12 稳定阶段变形区示意图Fig.12 Diagram of deformation area in steady stage
罗云华等[28]和牛卫中[29-30]在计算内翻模式准静态稳态力以及Rajabiehfard 等[31]在计算内翻全过程动态翻转力时均采用圆管中线曲率不变的几何模型,即管件中线曲率始终等于弯曲半径rAi,如图12中ABL为曲率不变的1/4 圆.然而实际翻转过程中由于管件外壁受模具限制且需考虑管壁增厚,所以管壁的增厚只能向着模具圆心的方向进行,即管壁中线逐渐背离模具.直到与模具分离时,B点为本文理论模型给出的管壁中点,BL为曲率不变几何模型给出的管壁中点.显然本文考虑AB段曲率变化的模型更符合内翻模式的变形模式.
本文理论模型假设管件在离开模具(即离开B点) 后,管件中线曲率半径仍然变化,直至达到C点的曲率半径rCi.由于不能确认相比B点曲率,C点曲率是增大还是变小或者不变.因此图12 中未给出本文理论模型中C点位置的示意.如若管件在离开模具后曲率不变,壁厚向中线两边同等增厚,则管壁中线如图12 中的,其对应成形半径等于式(8)得到的B点曲率半径rBi.本文成形半径rCi理论结果由式(11)得到,曲率不变几何模型对应成形半径等于式(5)得到的弯曲半径rAi.图13 给出上述成形半径理论结果与数值结果的对比,对比结果显示,本文成形半径理论结果rCi更接近数值结果.因此可以验证本文对于变形模式的假设是合理的.
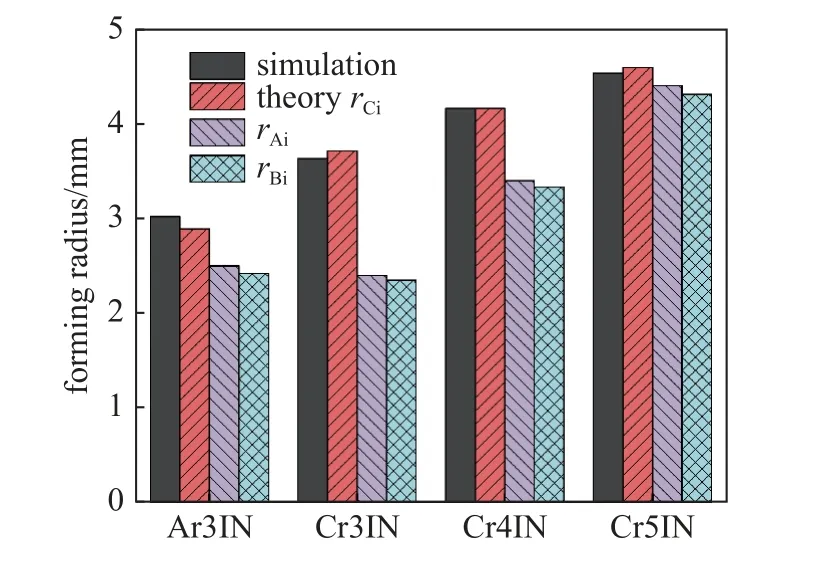
图13 成形半径的数值结果与不同理论结果对比Fig.13 Comparisons of the simulation and different theoretical results of the forming radius
图14 分别给出管A 和管C 在不同模具半径r上内翻转时B,C两点曲率半径之差.结果显示,对于尺寸确定的圆管,存在临界模具圆角半径rm使得B,C两点曲率半径相同.当圆角模具半径小于临界圆角模具半径时,C点曲率半径大于B点曲率半径;当圆角模具大于临界圆角模具半径时,C点曲率半径小于B点曲率半径.求解关于模具圆角半径的方程即可得到临界模具圆角半径rm.其中rBi和rCi分别为式(8)和式(11)表示的B,C两点的曲率半径.
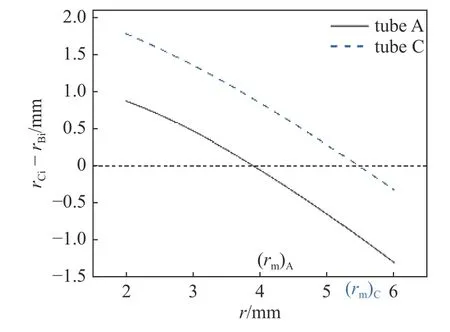
图14 管A 和管C 在不同模具半径r 上内翻转时B,C 两点曲率半径之差Fig.14 The difference value between rCi and rBi versus die radius
即当模具半径较小时,成形半径大于B点曲率半径;当模具半径较大时,成形半径小于B点曲率半径.
由于管壁增厚效应随着周向收缩程度的增加而增加,而成形半径体现周向的收缩程度,因此根据本文成形半径得到的成形壁厚更为准确.Rajabiehfard等[31]得到平均半径为14.6 mm,壁厚为1.2 mm 的不锈钢管在模具半径为3 mm 的模具上内翻的成形壁厚为1.85 mm.文中给出成形壁厚理论结果为1.735 mm,其与试验结果误差为6.2%.而根据本文理论模型得到成形壁厚为1.811 mm,误差为2.1%.由此可见,本文理论模型能够较好地预测成形壁厚.
3.3 内翻模式耐撞性的参数分析
本文选取稳态力、总吸能和比吸能3 个吸能指标来评价翻转模式的耐撞性.3 个吸能指标均可通过力位移曲线得到,且本文理论模型得到的力位移曲线已在3.1 节中经过试验和数值结果验证.因此,本文理论模型可用于讨论圆角模具内翻模式的吸能特性.为了便于讨论,本节全部使用管A 的材料参数计算吸能指标.圆角模具半径,圆管初始壁厚以及圆管平均半径对吸能指标的影响分别如图15~图17所示,其中摩擦系数取0.

图15 模具半径对吸能指标的影响Fig.15 Crashworthiness indicators versus the die radius
3.3.1 模具半径的影响
圆管内翻时,模具半径过小会引起管壁屈曲;过大会引起管端起皱,最终管壁同样发生屈曲.根据式(30)给出的翻转力表达式以及图15(a)给出的稳态力与模具半径的关系可知:当模具半径大于临界模具圆角半径时,内翻稳态力与模具半径呈单调递增关系;当模具半径小于临界模具圆角半径时,存在一个局部最优模具半径rop使稳态力取极小值.
表5 给出图15 中的3 种尺寸管的局部最优模具圆角半径和临界模具圆角半径及其分别对应的内翻稳态力.由表5 可得,局部最优模具半径使得内翻稳态力最小.但由于求解局部最优半径时需要对稳态力表达式进行复杂的求导计算,且局部最优模具半径与临界模具半径两者差距较小.因此本文取临界模具半径为全局最优模具半径.即当模具半径取临界模具半径时,稳态力取得最小值.同理根据图15(b)和图15(c)认为,临界模具半径同样使得总吸能和比吸能取最小值.
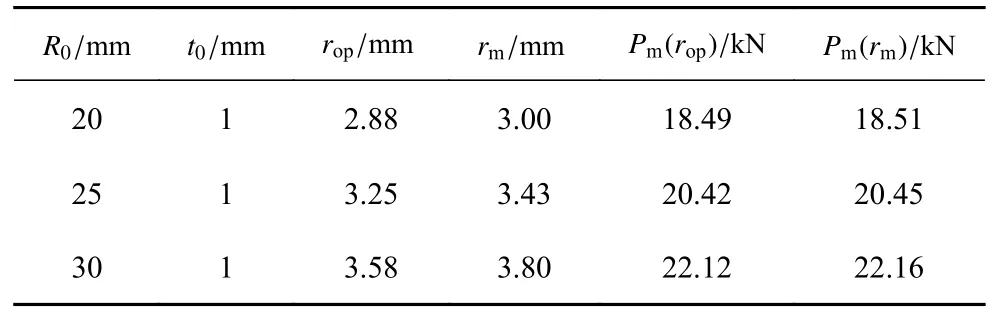
表5 局部最优模具圆角半径和临界模具圆角半径及其对应稳态力的对比Table 5 Comparisons of the local optimum die radius,the critical die radius and their corresponding steady inversion forces
3.3.2 圆管壁厚的影响
圆管壁厚过小会容易引发管壁屈曲失稳,不能成功翻转;管壁过大,则不能沿着模具半径弯曲从而不能成功翻转.由图16 可得稳态力、总吸能和比吸能均随着圆管壁厚的增大而增大.因此,可在成形范围内通过增大圆管壁厚以提高内翻模式的吸能特性.对于圆管平均半径为20 mm,模具半径为3 mm的内翻工况.当壁厚从1 mm 增长到1.2 mm 时,内翻稳态力从18.51 kN 增长到24.55 kN,增长了32.63%;总吸能从0.9 kJ 增长到1.19 kJ,增长了32.22%;比吸能从25.86 kJ/kg 增长到28.57 kJ/kg,增长了10.48%.由图16 (a)和图16(b)可得模具半径对于稳态力和总吸能随壁厚增大的增长率影响不大.在上述1~1.2 mm 的壁厚增长区间内,模具半径为3 mm 的比吸能曲线增长率大于模具半径为4 mm和5 mm 的曲线.然而其10.48%的增长率仍然低于内翻稳态力和总吸能的增长率(32.63%和32.22%).因此得到,增加圆管壁厚对于其稳态力和总吸能的提高要远大于比吸能.
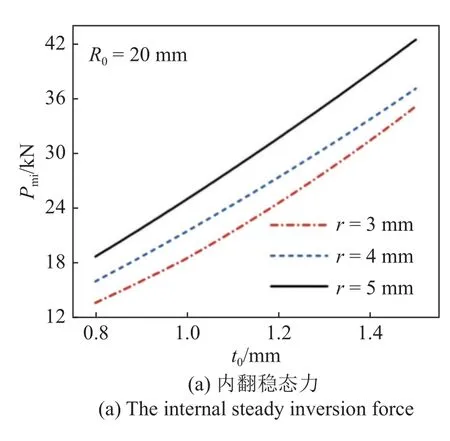

图16 圆管壁厚对吸能指标的影响Fig.16 Crashworthiness indicators versus the tube thickness
3.3.3 圆管平均半径的影响
由图17 可得,当圆管壁厚不变时,随着模具半径增大,圆管平均半径对稳态力与总吸能的影响减小.当模具半径为5 mm 时,圆管平均半径几乎不影响稳态力与总吸能的值.由于圆管质量的影响,比吸能则随着圆管平均半径的增加而降低.且随着模具半径增大,圆管平均半径对比吸能的影响增大.因此在选择平均半径时,除了考虑成形范围,还应综合考虑总吸能和比吸能的需求.
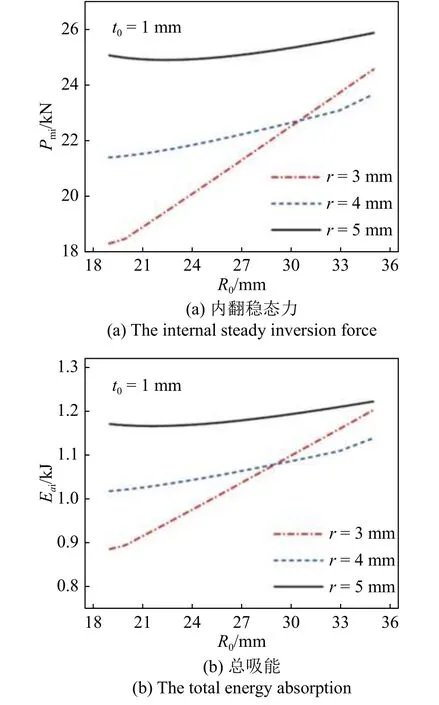
图17 模具半径对吸能指标的影响Fig.17 Crashworthiness indicators versus the tube average radius
4 结论
本文根据试验和数值模拟得到的内翻变形模式特点,建立了一个新的内翻理论模型.并通过与前人理论结果和试验结果的对比,得到本文理论结果更符合试验和数值结果.最后利用验证后的理论模型对内翻模式进行了耐撞性参数分析.本文得到主要结论如下.
(1)本文理论模型能同时考虑内翻过程的变形区曲率变化和管壁增厚,且其得到的成形半径和成形壁厚理论值更接近试验与有限元结果.
(2)本文理论模型得到的内翻稳态力的理论结果相比罗云华等[28]理论结果更接近试验和有限元结果.
(3)本文理论模型能准确得到内翻全过程的力位移曲线.进而得到总吸能和比吸能的理论结果,为分析内翻模式耐撞性提供理论依据.
(4)根据内翻模式理论结果得到:存在临界模具半径使得内翻稳态力总吸能和比吸能均取得最小值;圆管壁厚的增加使得吸能指标均增大,但是对比吸能的增长效应较低;圆管平均半径的增加使得内翻稳态力和总吸能均增大,但是会降低比吸能.

