硬磁软材料输流管的屈曲不稳定性分析1)

马地龙 王 琳 ,2) 陈 伟 †,,3)

* (华中科技大学航空航天学院工程力学系,武汉 430074)

† (华中科技大学机械科学与工程学院,武汉 430074)

** (智能制造装备与技术全国重点实验室,武汉 430074)

引言

输流管道是一类典型的工程结构,广泛应用于海洋工程、航空与航天工程、核反应器[1]等重大工程领域.Bourriéres[2]是输液管动力学研究的先驱之一,他推导了管道的线性振动方程,并以悬臂边界为例开展稳定性研究.Niordson[3]对两端简支管道在输送流体时的失稳行为进行了研究.他们的研究发现[2-3],管道的固有频率会随管内流体速度的变化而改变.Handelman[4]通过求解输流管系统的矩阵特征值,研究了系统的稳定性行为.通过综述前人大量研究工作,Paidoussis[5]全面总结了输流管动力学稳定性的4 种问题:(1) 内部流体作用下细长管道的稳定性;(2) 轴向外流作用下细长管道的振动响应;(3) 层间流体作用下共轴圆柱壳体结构的动力学行为;(4) 横向外流作用下管束的涡激振动响应.这一系统性的综述论文为后续的深入研究提供了重要参考.

随着工程实际结构对可靠性要求的不断提高,输流管道[6-7]的动力学分析和调控得到了迅猛发展.典型的应用场景包括热交换管道、空中加油管道、火箭发动机燃油管道和喷墨印刷的供墨管道等.输流管道的动力学行为实质上是流体与管道结构的相互作用(流固耦合作用),内流可以产生出作用于管道上的离心力和科里奥利力,同时管道变形或振动又会对内流的流动行为造成影响.此外,这种流固耦合行为还会受到诸如结构与流体属性[8-9]、边界条件和外部激励[10-14]等因素的影响.例如,Wang 等[15]对松动支撑下输流管道的非线性动力学行为进行了研究,揭示了间隙约束的几何和物理参数对管道稳定性和振动行为的影响规律.Oyelade 等[16]研究了输送两相高压热流体时微弯管道的动态稳定性,揭示了两相流及几何缺陷等参数对管道动力学行为的影响机制.

近年来,学者们在认识输流管振动机理的基础上,正进一步研究系统稳定性和动力学行为的调控技术.比较常用的调控方法是采用弹簧-阻尼组合下的减振器进行被动调控,如非线性能量阱[17-18]、惯容器[19-20]等.然而,这类方法并不适用于软材料输流管的动力学调控.上述减振器本身具有一定质量,虽然适用于金属等弹性模量较大的管道,但容易局部改变软质管道的横截面形状.因此,有必要提出适用于软材料管道的新调控方法.

近年来,有研究报道显示,活性材料结构在外加电[21-22]、光[23]、热[24]和磁[25-29]等外场调控下可实现力学行为的调节,并被认为是一种很有潜力的新调控技术.相较于其他物理场调控,磁场调控具有力输出大、响应迅速和无线操控等优势[30-31].最近,一种通过在软材料基底里嵌入硬磁颗粒制作而成的新材料[32]引起了研究人员的广泛注意.这类磁学上硬、力学上软的材料被称为硬磁软材料.为了满足不同磁性器件的功能性及结构性要求,可采用3D 直写打印的方法来制成所需元件[33-34].例如,可将硬磁颗粒或离散磁铁嵌入到高弹体基质中,将其加温至熔融状后从喷嘴挤出,之后再通过调控喷嘴附近的磁场方向,可实现各种磁活性细长结构的磁化矢量[35]可编程化制造.

硬磁软材料因其性能优越,被认为有巨大的工程应用潜力.例如,磁调控下的胶囊机器人[36]和微纳机器人[37]可以沿着血管或消化系统进入人体,完成活检和药物运送.还有报道显示,一类磁驱软体机器人[38-39]通过磁调控可在大脑狭窄的血管中行进并完成药物输送.Wang 等[40]设计了一种清除血栓的磁软导线,通过磁控制可将导线精准地伸入到血管内部,直达病灶部位并完成清除工作.总体而言,硬磁软材料的磁学性质较为稳定,可用于受限空间内的无线操控.正因为如此,磁调控方法备受关注.

特别地,对于输送药物的新型医疗器械来说,将流体器械设计成管状结构是一种可能方案.但是,现有的管状硬磁软结构的力学分析及其应用研究主要集中在没有内部流体(药物)的理想情形,而基于硬磁软材料技术的输流管磁调控的研究工作还较少.Chen 等[30]首次研究了硬磁软材料制成的输流管道的动力学行为和稳定性.Guo 等[25]分析了局部磁化的硬磁软管的静变形、动态稳定性和非线性动态响应问题.Dehrouyeh-Semnani[41]将输流管磁驱控制的应用场景拓展至非均匀磁化构型.需要指出的是,当前这方面的研究主要集中于悬臂输流管道问题,很少涉及两端支撑边界条件下的输流管道问题.事实上,在海底输油/输气管、航空加油管和核工程传热管等诸多应用场景中[42],柔性管道大都具有两端支撑的边界条件.而磁调控下的微创手术、药物输送等领域[38-39]所采用的硬磁软材料管道,其两端边界条件比较复杂,还可能是时变的,故不可简单地视为悬臂边界条件.为此,有必要进一步研究两端支撑条件下输流管道的磁调控原理.

基于以上分析,本文着重研究上端铰支、下端可轴向滑动铰支的输流管道系统的硬磁调控特性.首先基于Hamilton 原理,推导了铰支-可滑动铰支边界下硬磁软材料输流管道的非线性动力学方程;然后,通过Galerkin 离散方法实现了模型降阶,并在此基础上分析了管道的稳定性,计算了管道的非线性力学响应;最后,对输流管道的后屈曲行为进行了参数分析,并得出一些重要结论.

1 硬磁软材料输流管力学模型

1.1 动力学模型

本文考虑由硬磁软材料制成的单位长度质量为m的输流管道,其长度为L,密度为ρ,弯曲刚度为EI,横截面积为A;管道输送流速为U的不可压缩流体,流体单位长度质量为M.如图1 所示的坐标系,外加磁场的磁通量密度Ba是均匀的,其方向与x0轴正方向之间的夹角为α,管道变形前后的残余磁通量密度分别记为和Br.

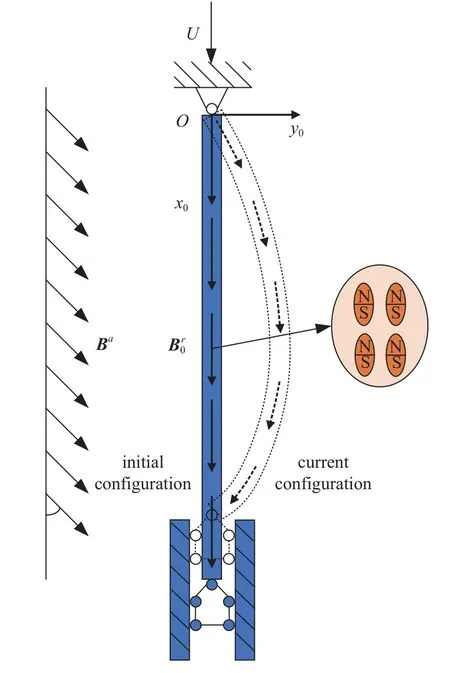
图1 铰支-可滑动铰支硬磁软材料输流管模型Fig.1 A hard-magnetic soft pipe conveying fluid with an upstream pinned end and an axially sliding downstream end

为了简化硬磁软材料输流管道动力学控制方程的推导过程,本文引入以下假设:(1)初始状态下,管道变形前呈直线形状并竖直向下,管轴线与x0轴正方向一致;(2) 管道边界条件为铰支-可滑动铰支;(3)管道细长且轴线不可伸长,因此欧拉-伯努利梁理论是适用的;(4)管道仅在竖直平面内变形或运动;(5)管内流体的流动为定常流动;(6)管道是均匀磁化的,即残余磁通密度大小恒定,方向总是沿着梁的轴线方向向下.

在后续分析中,u和w依次记为管道轴线的轴向位移和横向位移,θ为管道变形后轴线的转角,dx0和ds分别表示管道单元变形前后的长度.根据管轴线不可伸长假设,dx0=ds.因此,管道的轴线位移可表达为[26]

结合管道初始形态,管道变形后的轴线位置矢量xi+yj的两个分量x和y可表示为

输流管系统的总动能包括管道动能和流体动能两部分,其变分为

其中“·”代表对时间变量t求导数,“′”代表对空间变量x0求导数.

系统势能由弹性势能、重力势能以及磁势能3 部分组成,其中系统弹性势能的变分式为[5]

式中I是管道横截面关于中性轴的惯性矩.

输流管系统重力势能的变分式为

其中g是重力加速度.式(5)涉及到δx,由于控制方程的推导需要统一变量变分,因此需要找到δx与δy之间的关系,这需要借助不可扩展性条件来进行.在铰支-可滑动铰支边界下,基于x0=0 处的δy=0,可得[5]

通过使用变分积分交换式[5]

经过变换,最终得到重力势能的变分式为

所考虑的外加磁场Ba为恒定磁场,磁场方向与轴x0之间的夹角为α,其表达式为

根据假设(6),硬磁软材料管的非均匀残余磁通量密度在各分段中是均匀的,残余磁通密度Br为

由于变形后剩余磁通密度的方向仍与管道的轴线一致,当前构型下管道的磁势能密度为[26]

将式(11)沿着管道横截面和长度积分,再变分后可得到磁势能变分式如下

本文考虑的输流管道系统包括动能T、弹性势能V、重力势能G和磁势能Vm这4 个部分,因此,系统的拉格朗日函数 L 可写成

因管道末端可以轴向移动,故本文考虑的输流管属于开放系统,其相对应的扩展Hamilton 原理为[5]

本文考虑的软质管道具有黏弹性属性,此时需要在方程中添加耗散项.根据Kelvin–Voigt 型[1]黏弹性本构模型,可将前文中的弹性模量更换为相应的黏弹性形式,即

其中b为材料中的Kelvin–Voigt 阻尼系数.进行黏弹性修正后,将式(3)、式(4)、式(6)、式(8)和式(12)代入式(14)中,可得到硬磁软材料输流管系统的振动控制方程如下

磁调控方法是通过外加磁场对磁性材料施加磁场作用力,从而实现对管道的稳定性和弯曲变形的调控.本文所考虑的管道是通过往橡胶等软质材料中有序嵌入微磁颗粒而制成,表现出磁活性.从力学上来讲[40,43],均匀磁化管道在均匀外磁场作用下所受的磁场力表现为端部的集中力.式(16)中最后一项就是参与系统做功的磁场力轴向分量相关项.为便于后续研究,引入以下无量纲参数

其中,β是单位长度管内流体的质量与单位长度输流管系统质量之比,μ是无量纲的黏弹性系数,v是无量纲流速,γ是无量纲重力参数,P是无量纲磁场力,η是管道轴线的无量纲横向位移,ξ和τ分别是管道系统的无量纲空间坐标变量和时间变量.将式(17)代入方程(16),管道的非线性振动方程可重新写成以下的无量纲形式

2 求解方法

本节将对系统的振动控制方程求解.首先,采用Galerkin 离散方法将偏微分方程(18)降阶为有限数量的常微分方程组,再采用4 阶变步长龙格-库塔方法进行迭代求解.

2.1 数值离散方法

首先对含有二阶时间偏导数的非线性项进行转化,可借助下式完成[5]

非线性黏弹性项对结果影响有限,在计算过程中通常只保留其中的线性黏弹性项[1].因此,转化后的非线性偏微分方程可写成

铰支-可滑动铰支相对应的边界条件为

基于Galerkin 数值离散方法,管道轴线的横向位移可近似写成

式(23)中的非线性项可以使用矩阵变换[6]的方法得到,具体形式如下

方程组(27)可采用Matlab 程序中的ODE45 函数实现变时间步长的龙格-库塔方法求解,其中

2.2 收敛性分析

为了确保Galerkin 近似的精度,需要选择合适的N并进行收敛性分析.参照文献[1,26],我们选取以下计算参数和初值,基于方程(20)进行收敛性分析

除q1外,其他广义坐标的初值均取为0.

不同模态截断数N取值下,管道中点横向位移随内流速增大的分岔曲线如图2 所示.图中选取了N为4,5 和6 的3 种情况.可以发现,当N=5 时,Galerkin 截断近似的结果已经收敛.因此,本文在后续的计算中均选取N=5 开展计算.

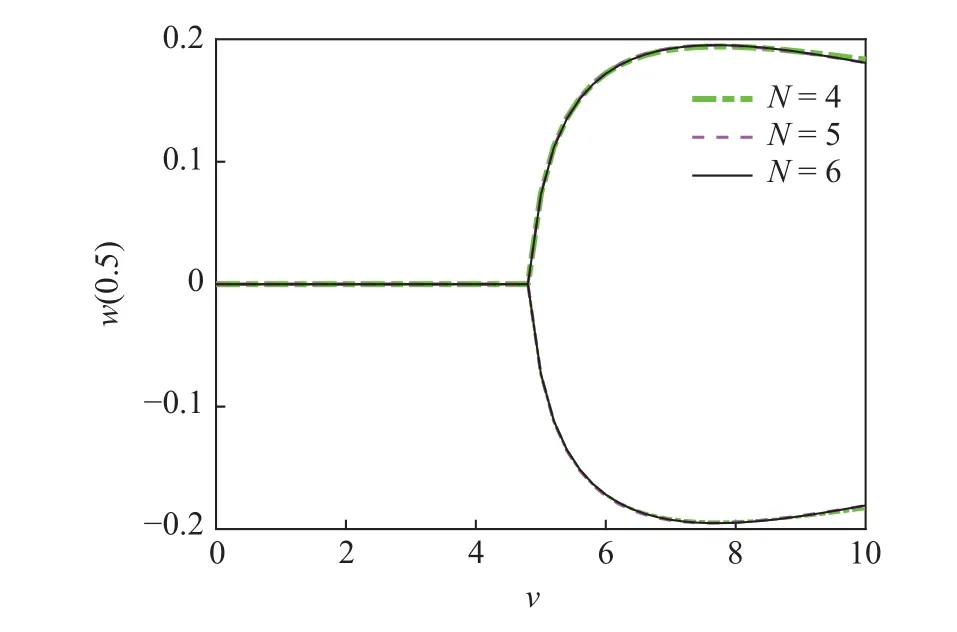
图2 不同模态截断数N 下以流速为控制变量的管道中点横向位移分岔图Fig.2 Bifurcation diagram for the midpoint's transverse displacement of the pipe with various flow velocities when different values of N is chosen for calculations

3 稳定性分析

3.1 线性频率分析

为了判断管道系统的失稳形式,需要分析输流管系统的线性动力学行为,方程(20)的线性化形式为

本节通过Galerkin 方法离散方程(30),求解时仍沿用式(29)中的无量纲参数.

图3 给出了输流管系统前3 阶特征值随流速变化的演化曲线,其中Im(ω) 代表无量纲振动频率,Re(ω)为与管道阻尼有关的特征值实部.由图3 可知,随着流速的增大,输流管系统的第一阶振动频率Im(ω)减小,但Re(ω)保持不变;当流速增大至某一临界值时,第一阶模态的Im(ω)减小至0;当流速大于该临界值时,第一阶模态的Im(ω)=0,此时对应的Re(ω) >0,管道将发生屈曲失稳.以上计算结果表明,管道在临界流速下发生了第一阶模态的屈曲失稳,不会出现颤振失稳.对于边界条件为铰支-可滑动铰支的输流管道系统而言,这种静态失稳方式是合理的.当内流速超过临界流速之后,线型模型预测的固有频率是关于未变形管道的直线构型[44-46],不是关于屈曲位形,因此上述分析存在一定的局限性.但是,本文更为关注的是在结构失稳之后磁调控对屈曲构形的影响,因此进行特征值分析的主要目的是得到临界流速值.

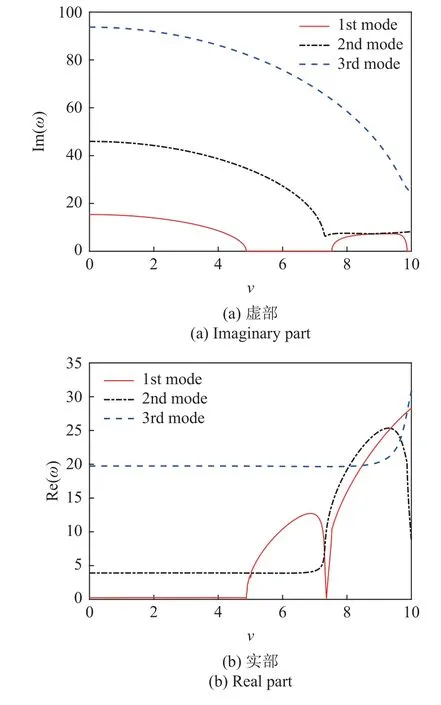
图3 输流管系统前3 阶特征值随流速变化的结果Fig.3 The variation of the first three eigenvalues of the fluid-conveying pipe system with various flow velocities

3.2 临界流速分析

图4 给出了临界流速vcr随磁场力P及磁偏角α增大的变化图.如图4(a),当α=π/3 时,令P值从0 增大到20,临界流速单调增大;在图4(b) 中,当P=10 时,令α值从0 增大到2,临界流速逐渐减小.可以得出,单独改变P或α会使得临界流速单调增大或减小.

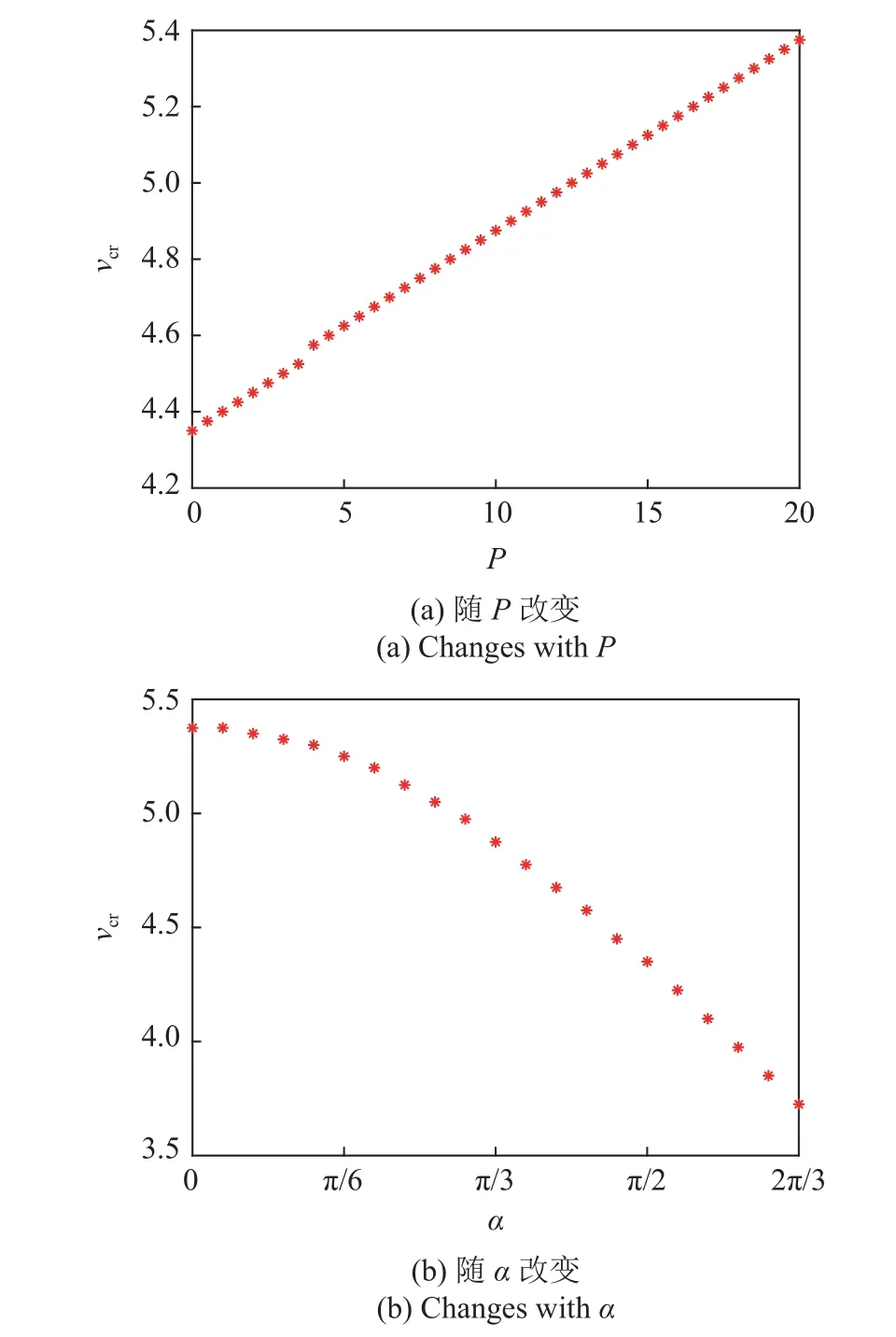
图4 输流管系统临界流速随参数变化的结果Fig.4 The result of the change of critical flow rate of the pipeline system with parameters

临界流速vcr既受到磁场力P的影响,也受到磁偏角α的影响,这是因为磁力项是由这两个参数组成的.因此,在利用磁场力调控系统稳定性时,需要同时考虑磁场力的方向及其大小.

4 非线性行为分析

4.1 对比验证

在本节中,令磁场力P=0,从而将磁力项退化,再与Jiang 等[1]的理论结果进行比较,以验证本文求解非线性问题的正确性.图5 对比了本文结果与Jiang等[1]退化到二维平面问题的计算结果,可以看出:当磁力项退化为0 时,两者结果完全一致,从而证实了本文计算程序是可靠的.

图5 磁场力为零时管道中点横向屈曲位移的分岔图结果对比Fig.5 Comparison of bifurcation results of the transverse buckling displacement at the midpoint of the pipe when the magnetic field force is zero

4.2 初值条件的选取

对于静态分岔,初值条件的选取可能对其计算结果产生影响,因此需要选取合理的初值条件,使计算结果能够涵盖所有可能的稳态解.本节沿用式(29)中的参数,取广义坐标q1=±0.0025,±0.0125,±0.025 和 ±0.05 为非零初值进行计算.

从图6 和图7 可以看出,当流速低于临界流速时,输流管保持静止,此时管道处在零平衡位置;当流速高于临界值时,输流管系统发生静态屈曲失稳.随着流速增大,输流管中点屈曲位移将出现“先增大后减小”的现象,输流管道下游端的轴向位移同样出现了这样的趋势,但其在高流速下的幅值变化较小.

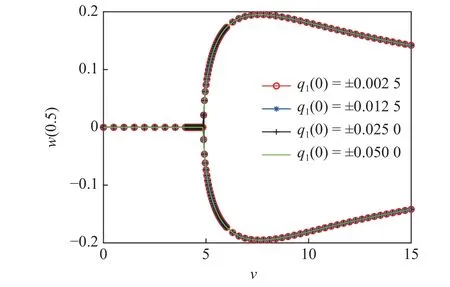
图6 不同初值条件下管道中点屈曲位移分岔图Fig.6 Bifurcation diagram of pipe midpoint's transverse buckling displacement for different initial conditions

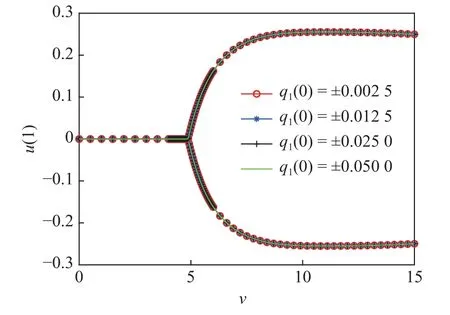
图7 不同初值条件下管道末端轴向位移分岔图Fig.7 Bifurcation diagram of the tip end's axial displacement of the pipe for different initial conditions

管道中点屈曲位移的最大值为0.2 左右,管道下游端轴向位移的最大值在0.25 左右,这两种位移处在相同的量级,因而都可以直观的从整体屈曲形状图观察到.本文计算发现,不同的初值下计算结果相同,因此下文中均以q1(0)作为初值开展计算.

4.3 磁场力和磁偏角对屈曲位移的影响

本节将分析磁场力P和磁偏角α对输流管非线性力学响应的影响,系统无量纲参数取值为β=0.142,μ=0.005,γ=18.9.

图8 展示了不同磁偏角α下磁场力对管道中点横向屈曲位移的影响.当流速小于临界值时,输流管在静态平衡位置保持静止;当流速大于临界值时,输流管以静态分岔形式发生屈曲失稳,且临界流速的大小会受到磁场力的影响.

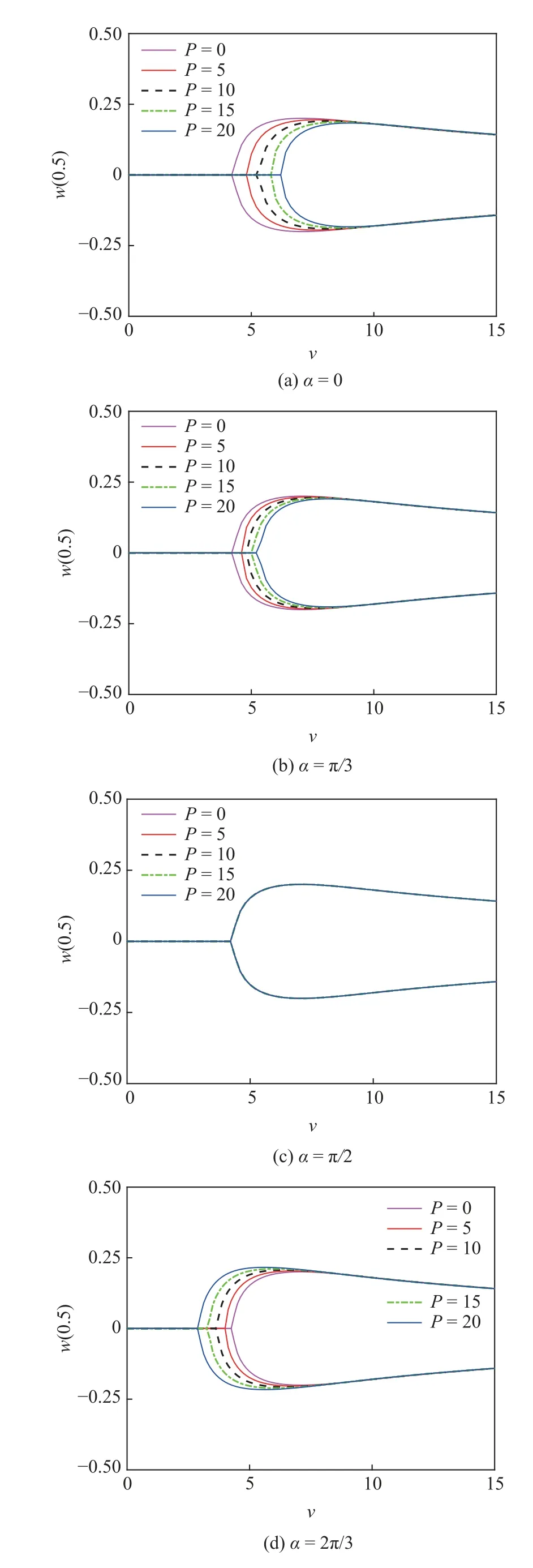
图8 不同磁偏角下管道中点横向位移分岔图Fig.8 Bifurcation diagrams for the lateral displacement at the pipe's

当α<π/2 时,磁调控的效果表现为增大其临界流速,抑制管道失稳.若以磁偏角α=π/3 时的分岔图为例,磁场力P=0 时,临界流速最小,磁场力P的增大会导致输流管的临界流速也随之增大.这种磁调控的效果会随着α接近π/2 而减小,当α=π/2 时,磁场力的影响完全消失.当α>π/2 时,磁调控的效果表现为减小其临界流速,加剧管道失稳.例如,当α=2π/3 时随着磁场力P的增大,输流管的临界流速逐渐减小.

图9 展示了不同磁偏角α下磁场力对管道下游端轴向位移的影响,其变化趋势与管道中点横向屈曲位移一致,即:当流速小于临界值时,输流管在零平衡位置保持静止;当流速大于临界值时,输流管以静态分岔形式发生屈曲失稳,且临界流速的大小会受到磁场力的影响.当α<π/2 时,随着磁场力P的增大,输流管的临界流速也逐渐增大;当α=π/2 时,磁场力的影响完全消失;当α>π/2 时,随着磁场力P的增大,输流管的临界流速会逐渐减小.

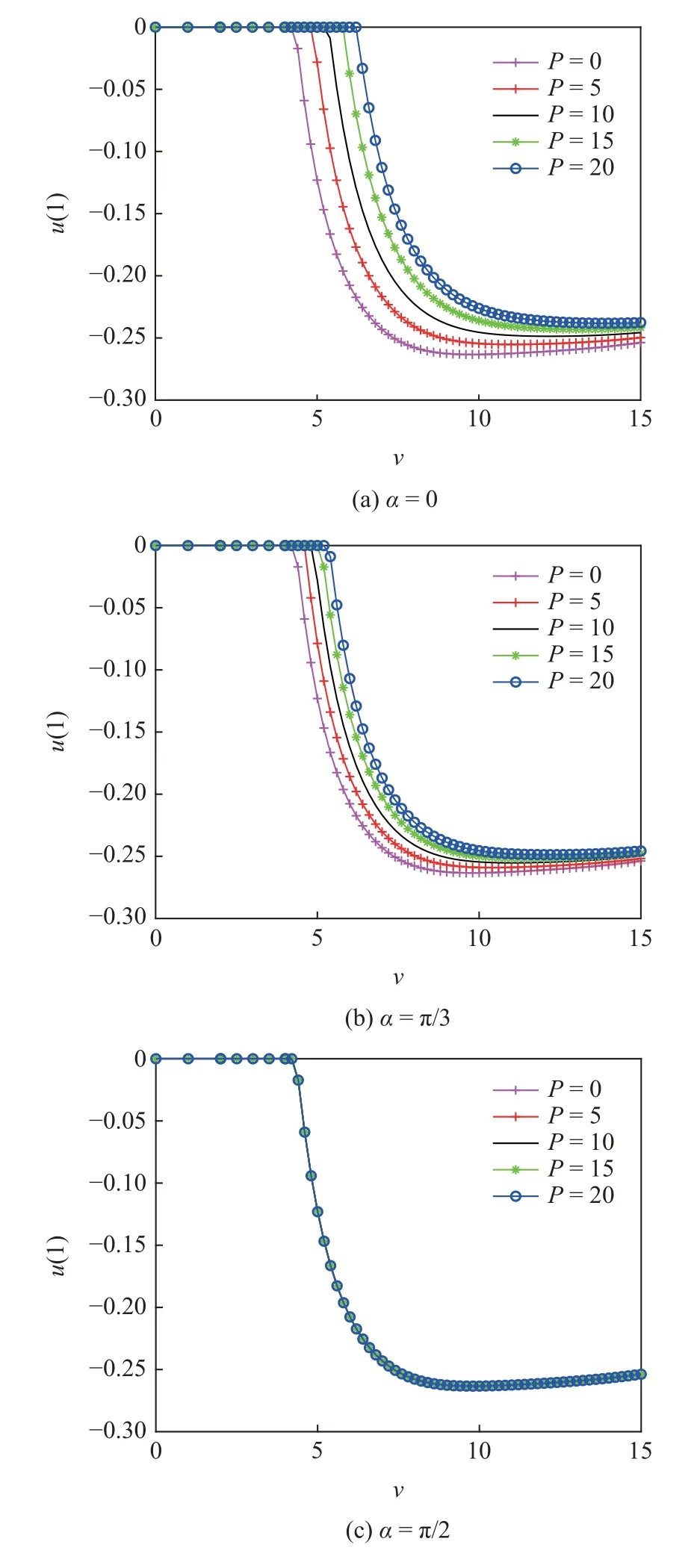
图9 不同磁偏角下管道下游末端轴向位移的分岔图Fig.9 Bifurcation diagram of axial displacement of downstream end of the pipe under different magnetic field forces

对于横向和轴向这两种位移而言,其幅值都随着流速呈现了“先增大后减小”的规律,且处在同一量级.另外还可以看到,磁场力P和磁偏角α对输流管系统的影响不是单独起作用的;在进行磁调控时,由磁偏角α决定磁场力P对输流管的影响趋势,磁场力P的大小决定了这种影响趋势的大小.

对比图8 和图9 不难发现,磁调控的作用直观的体现在对临界流速的影响上面.如果结合控制方程(18)中的磁场力项,可以发现磁调控过程中起主要作用的是垂直于管道初始构型的磁力项.输流管系统处于外加磁场当中,以初始构型为磁势能0 点,当内流速增大时,管道开始变形,若管道变形方向与横向磁场力方向相反,系统的磁势能开始增加,通过调整磁场力P和磁偏角α释放磁势能,可以提高系统的稳定性;若管道变形方向与横向磁场力方向相同,则通过增大磁势能就可以提高系统的稳定性.当内流流速继续增大时,进行调控所需要的外力也随之增大,此时磁调控的效果减弱,不同磁场力下的曲线相互靠近,如果想要达到更为理想的调控效果只需增大磁场力即可.

4.4 磁场力和磁偏角对管道屈曲形状的影响

本节探讨磁场力P和磁偏角α对输流管屈曲形状的影响,主要对4.3≤ν≤20 范围内的一些典型案例进行计算和分析.

图10 给出了α=π/3 时不同磁场力P下的管道屈曲形状.由该图可知,当流速大于临界值时,输流管发生静态屈曲,管道末端向着上端靠近;管道由直管逐渐变成类似于“L”形的管道,管道横向屈曲位移的最大值先增大后减小.随着流速的增大,管道屈曲位移最大值对应的位置逐渐远离上游端.

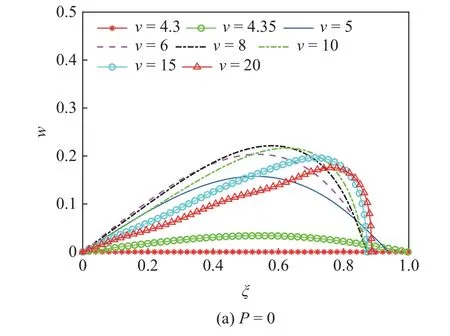
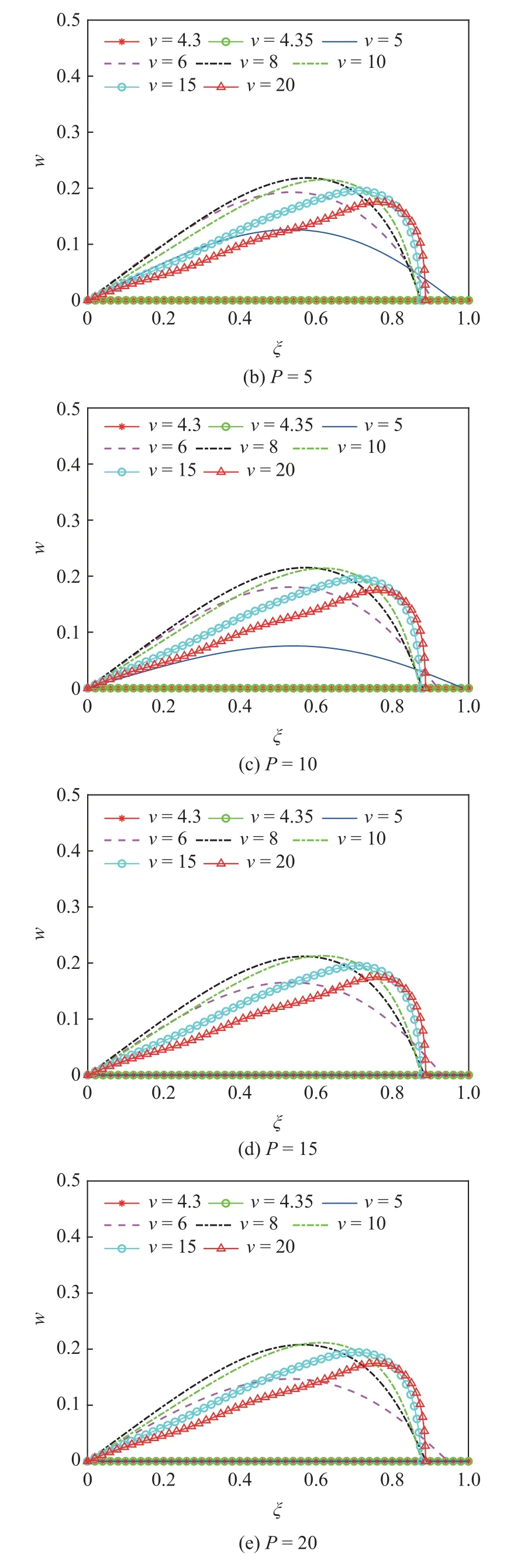
图10 不同磁场力作用下管道后屈曲构型图Fig.10 Post-buckling configurations of the pipe under the action of different magnetic field strengths

在磁偏角α=π/3 的情况下,横向位移最大值变化趋势仍为先增大后减小.对比P=0 和P=5 两种情况下的屈曲形状可以发现,P较大时管道发生屈曲失稳的临界流速v增大了,且管道变形的整体幅值都有所减小,这说明此时磁调控的效果表现为增大其临界流速,即抑制管道的失稳.

图11 给出了P=10 时不同磁偏角α下的管道屈曲形状.当流速大于临界值时,输流管发生屈曲,下游端向上游移动,横向位移最大值先增大后减小.对比不同磁偏角α下的屈曲形状图,发现当磁偏角α改变时,磁调控的效果也截然不同,这说明磁场力P和磁偏角α对输流管系统的影响不是单独起作用的.除此之外,图中管道的屈曲形状也并不是左右对称,这是由边界条件的不对称造成的.

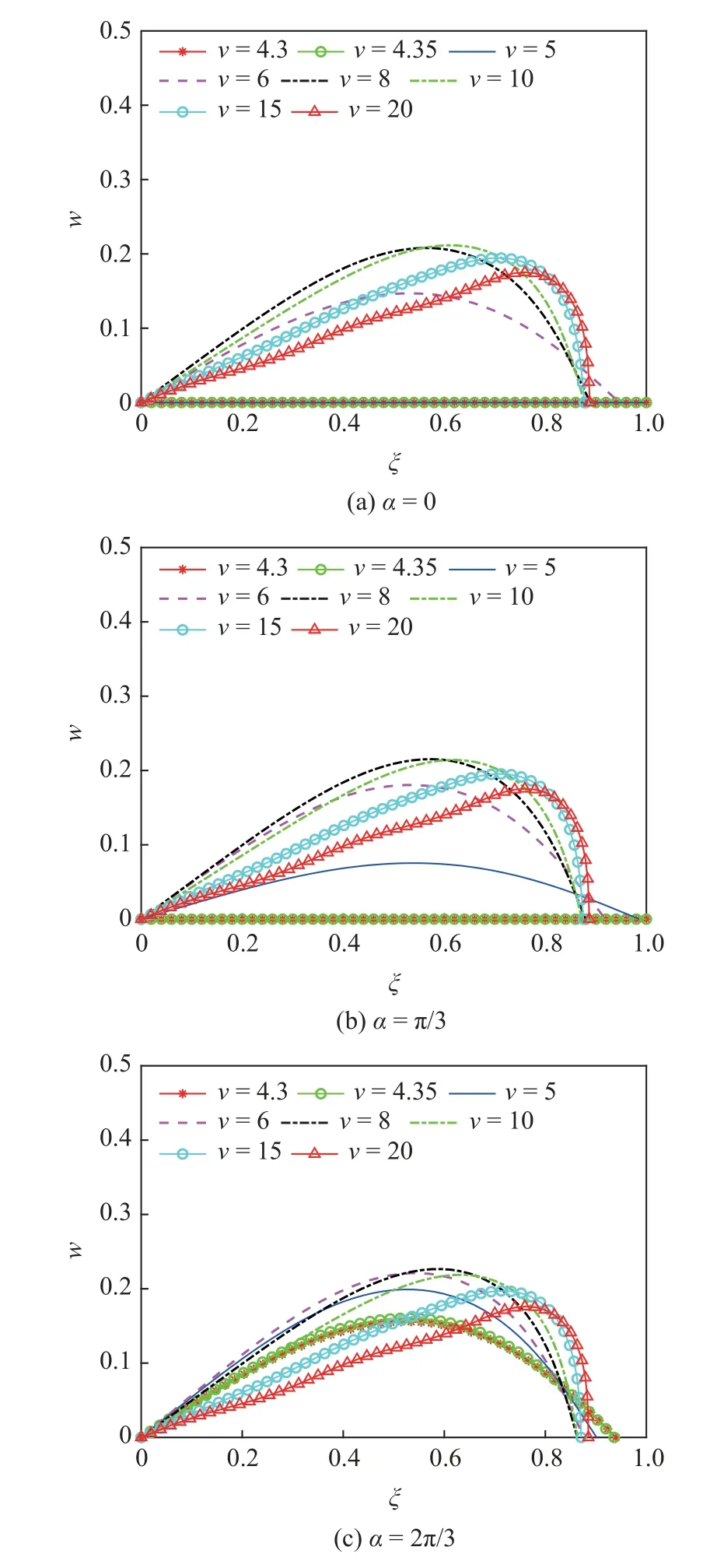
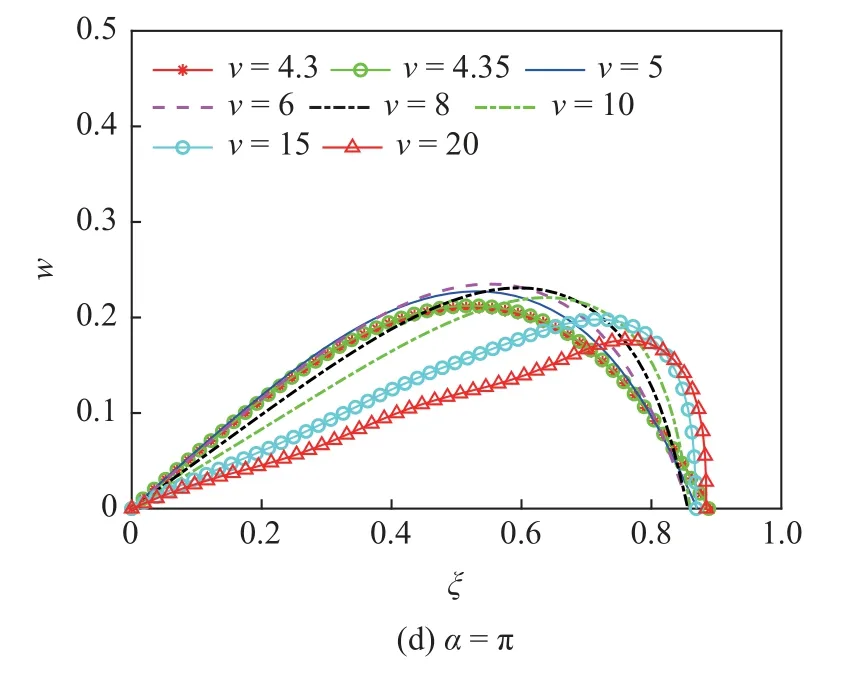
图11 不同磁偏角下的管道屈曲形状图Fig.11 Post-buckling configurations of the pipe under the action of different magnetic field angles

从力学机理角度对图10 和图11 进行分析,输流管道受到内流作用力、边界约束力、重力以及外部磁场力的作用,在不同流速下呈现出相应的构形.作用于管道的所有力可被分解为平行于管道初始构型的轴向力以及垂直于管道的横向力,其中垂直于管道初始构形的横向外部磁场分力是起到磁调控作用的主要因素,调节管道的构形只需从横向力方面入手,即调节磁场力P和磁偏角α.观察图10 的几幅图片可以发现,随着磁场力P的增大其横向分力也逐渐增大,管道的稳定性也逐渐提升,这也印证了上述机理.

5 结论

本文针对一端铰支、另一端可轴向滑动铰支的硬磁软材料输流管结构,试图采用外磁场来调控管道的非线性力学行为.基于Hamilton 原理,首先推导了硬磁软材料输流管的振动控制方程.其次,采用Galerkin 方法和变步长4 阶龙格库塔方法,离散和求解了非线性偏微分方程.然后,通过稳定性分析,发现当流速超过其临界值时管道会发生屈曲失稳.最后,通过考虑不同的磁场力P和磁偏角α,对管道系统的非线性力学响应进行了详细分析.本文得到的结论如下.

(1) 当流速小于临界值时,输流管在零平衡位置保持静止;当流速大于临界值时,输流管以静态分岔形式发生屈曲失稳.

(2) 磁场力P和磁偏角α共同影响输流管系统的稳定性.单独改变P或α会使得临界流速单调增大或减小.当α<π/2 时,随着磁场力P的增大,输流管的临界流速增大,此时磁调控抑制其失稳;当α=π/2 时,磁场力的影响完全消失;当α>π/2 时,随着磁场力P的增大,输流管的临界流速减小,此时磁调控反而加剧系统失稳.

(3) 当流速大于临界值时,管道因屈曲失稳而末端上移,并由直管形状逐渐变成“L”形状.管道横向屈曲位移的最大值先增大后减小,并且最大值对应的位置逐渐远离上游端.

本文建立的硬磁软材料输流管的非线性模型为预测软材料输流管的动力学行为提供了理论基础,同时也为输流管的磁调控提供了思路.需要指出的是,如果我们对磁势能进行修改,可将该模型拓展至非均匀磁化管道的流固耦合力学分析之中.本文所研究的磁驱调控具有非接触式、快速响应等优势,有望进一步应用于医用器械和极端环境作业等需精细调控的工程科技领域.