考虑空间位置差异的机床直线轴定位误差快速辨识方法*

刘传进 姚思涵 高卫国

（①南通国盛智能科技集团股份有限公司，江苏 南通 226003；②机构理论与装备设计教育部重点实验室（天津大学），天津 300350）

随着现代制造业的发展，机床在汽车、医疗设备和模具制造行业中的重要性日益凸显。由于龙门加工中心与坐标镗床等结构和加工条件的复杂性，其加工精度会受到各种误差的影响。其中，几何误差是主要的误差源之一[1]。快速、准确、全面的误差测量和辨识对机床精度性能的评价和工件加工精度的预测等具有重要影响。

机床直线轴几何误差可采用多种测量仪器进行测量。激光干涉仪通常用于直接测量直线轴的几何误差[2-3]，但测量过程繁琐耗时。在此基础上，Renishaw 及API 等公司推出了多光束激光干涉仪，可通过一次测量获得单个直线轴的6 项位置相关几何误差，但其在不同测量位置获得的几何误差存在差异[4]，难以适用于工作空间精度的全面预测和评价。球杆仪因其测量时间短、安装便捷的优点受到广泛关注[5-6]。但其测量范围受到球杆仪杆长的制约，且测量结果同样受到基座安装位置的影响。

激光跟踪干涉仪结合了激光跟踪仪与激光干涉仪的优势，基于多边法测量工作空间内任意位置的三维坐标。王金栋等[7]提出了一种基于多站分时测量的几何误差辨识方法，通过自标定确定测量点实际坐标，通过相应的测量轨迹获取距离数据，并基于最小二乘法辨识几何误差项。Deng M 等[8]通过考虑刚体运动约束提高了测量点坐标计算的准确性，测量过程中待测轴进行12 次重复运动，要求待测轴具备良好的重复定位精度。此外，Etalon 公司的TRAC-CAL 软件可以通过空间测量辨识三轴机床的21 项几何误差[9]，但所辨识误差未能考虑不同空间位置处的误差差异。

现行机床精度检测标准尚未关注测量位置差异对于几何误差测量值的影响，机床检验通则[10]中未能定义直线轴定位误差与测量位置的关系，以某一特定位置检测获得的误差值来表征机床整体的精度水平难免有失偏颇。

因此，本文提出一种考虑空间位置差异的机床直线轴定位误差快速辨识方法，以龙门机床为例，利用激光跟踪干涉仪测量机床的工作空间误差，进而辨识不同位置处直线轴的定位误差及空间体对角线误差。该方法通过自标定方法得到4 个基站在机床工作空间中的坐标值，进而，根据基站坐标计算测量点的空间误差。基于初始点与测量路径内测量点误差差异辨识直线轴定位误差及体对角线误差，并分析不同位置处的定位误差存在差异的原因。

1 基于跟踪干涉仪的空间坐标标定

基于激光跟踪干涉仪测量机床空间测量点与跟踪仪的相对距离，通过解析方法实现多基座及死径长度（dead path length，DPL）的自标定，进而计算机床空间测量点的实际坐标。

单台激光跟踪干涉仪可通过多站分时测量获得测量点在机床工作空间下的实际坐标[11]。测量过程如图1a 所示，激光跟踪干涉仪顺序安装在4 个非共面的基站位置上进行测量，通过4 组相对距离测量数据实现基站位置的标定。X轴测量范围为(-3 500,-1 500)，但其位于工件链，因此其在工作空间内的范围为(1 500,3 500)。Y轴测量范围为(-2 500,-500)，Z轴为(-1 250,-250)，测量点在机床工作空间的理想位置如图1b 所示。

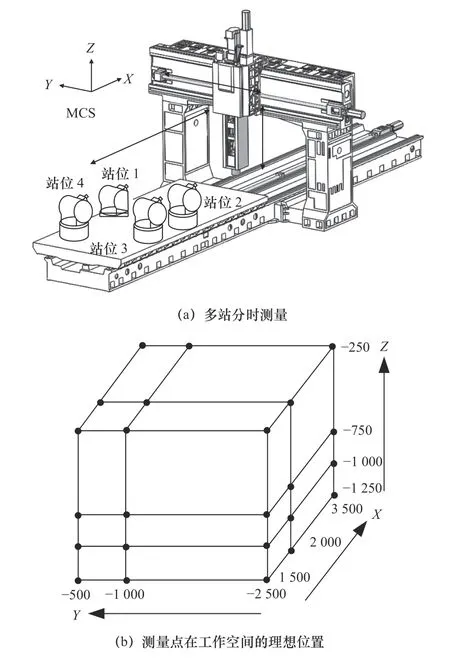
图1 工作空间实际坐标测量

测量过程中站位p1在MCS 下坐标为 (xp1,yp1,zp1)，激光跟踪干涉仪的DPL 为L1。测量点mi在工作空间的理想坐标为 (xi,yi,zi)且对应的跟踪干涉仪相对测距为Li,measured，则可构建形如公式（1）所示的最小二乘问题：

通过文献[11]所述方法求解该最小二乘问题，该方法可以得到式（1）的唯一解。分别计算四站测量过程中基站在工作空间的实际坐标及跟踪干涉仪的DPL，实现测量系统的自标定。对于第i个测量点的实际坐标 (xi,a,yi,a,zi,a)有：

每个测量点均可以构建形如公式（2）的超定方程组，进而求解方程组以计算测量点的实际坐标。本文采用无需初值的解析方法[11]计算测量点的实际坐标，并通过多次迭代提高坐标的计算精度。该坐标用于进一步辨识直线轴的定位误差及体对角线误差。

2 机床误差辨识

以X轴为例进行直线轴定位误差和空间体对角线辨识。选择X轴同向的空间测量点，基于首个测量点与其余测点的空间误差差异计算直线轴不同位置处定位误差。同时，根据测量点与初始位置实际距离与理想距离的差值获得空间体对角线误差。

2.1 直线轴定位误差辨识

测量点空间误差即为测量点实际坐标与理想坐标在X向、Y向及Z向的差值：

以X轴为例说明直线轴定位误差的辨识方法。初始测量点坐标为 (xx,yx,zx)，机床沿X轴正向移动距离X，激光跟踪仪每间隔一定距离进行一次测量。测量过程中Y轴及Z轴保持静止，则运动过程中实际坐标仅受到X轴几何误差影响。X轴定位误差EXX则为各测点X向空间误差 Δxi减去首个测点X向空间误差 Δx1。

该误差即为Y轴及Z轴坐标为 (yx,zx)时的X轴定位误差。同理，通过该方法可以计算Y轴及Z轴在不同位置下的定位误差。

2.2 空间体对角线误差辨识

龙门机床的工作空间如图2 所示，基于ISO 230-6: 2002 定义4 条体对角线，4 条体对角线命名和范围见表1。

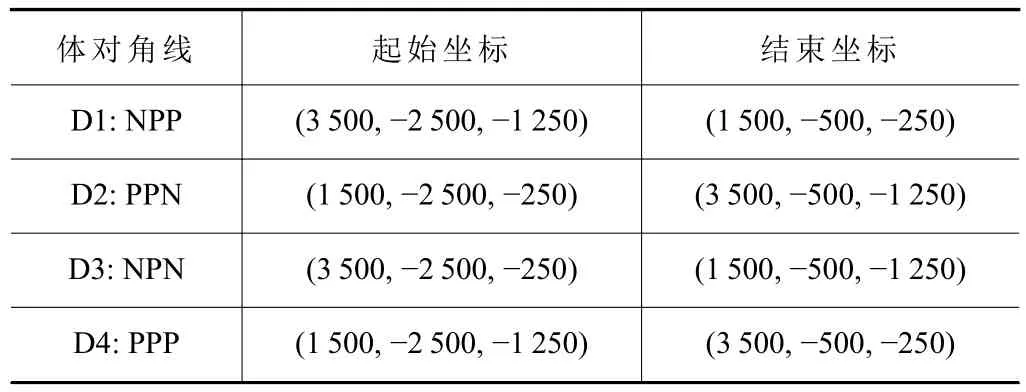
表1 空间体对角线范围

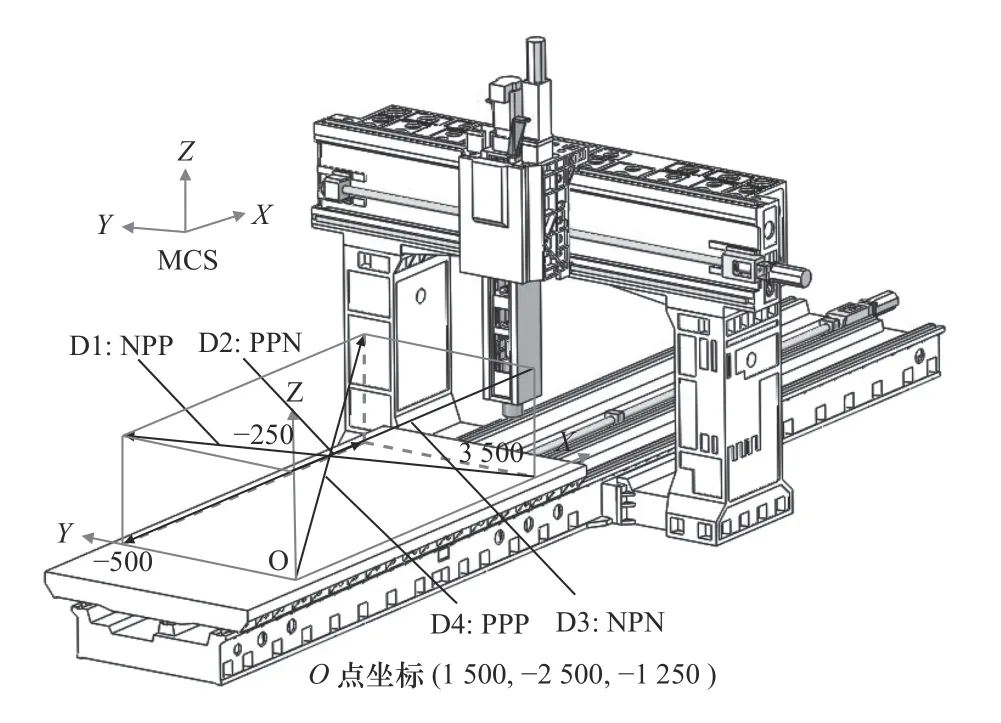
图2 空间体对角线定义

X轴与Y轴每隔500 mm 且Z轴每隔250 mm 测量一次，因此体对角线每相邻两测量点间理想距离为750 mm。测量点与初始位置的实际距离即为对角线的实际长度le。

le与理想距离750 mm 的差值即为体对角线误差de。

3 实验验证

基于跟踪干涉仪测量机床空间测量点的实际坐标，并通过所提出的方法辨识龙门机床的直线轴定位误差及空间体对角线误差（图3a）；同时，利用多光束激光干涉仪在某一特定位置进行直线轴6 维误差的测量（图3b），并对两种方法得到的直线轴定位误差进行对比分析。通过Renishaw XM60 多光束激光干涉仪测量X轴几何误差，测量时Y轴和Z轴坐标为(-1 255,-1 054)。测量实验重复3 次并取平均值，得到图4所示的X轴6 项几何误差。

图3 测量实验

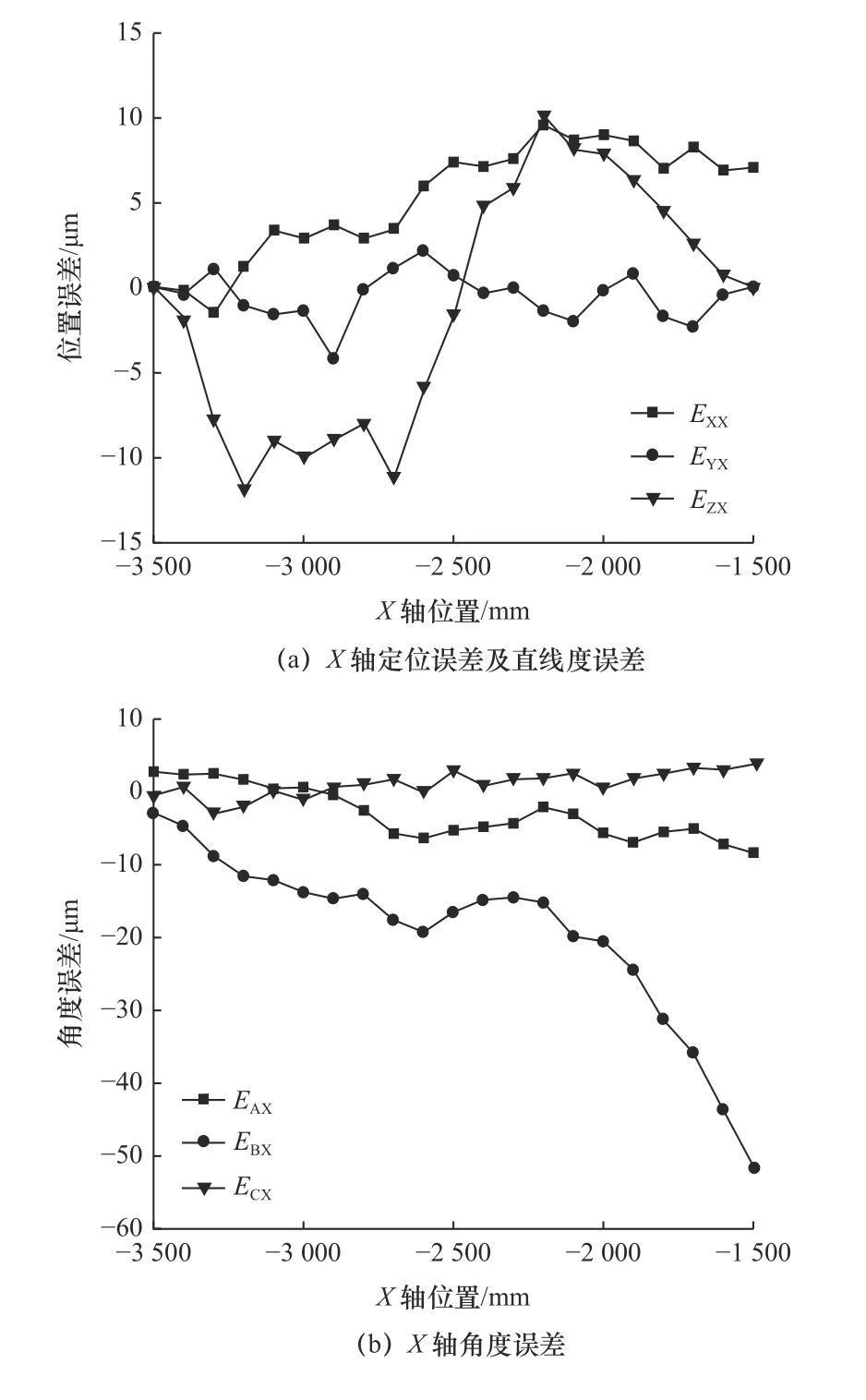
图4 X 轴几何误差测量结果

采用Etalon Laser Tracer-NG 激光跟踪干涉仪测量工作空间误差，以获取相对测距信息，跟踪干涉仪和反射镜分别安装在工作台及主轴上。根据空间误差辨识直线轴定位误差。以X轴为例，分别考虑不同Y轴位置及Z轴位置对于其定位误差的影响，定位误差结果如图5 所示。

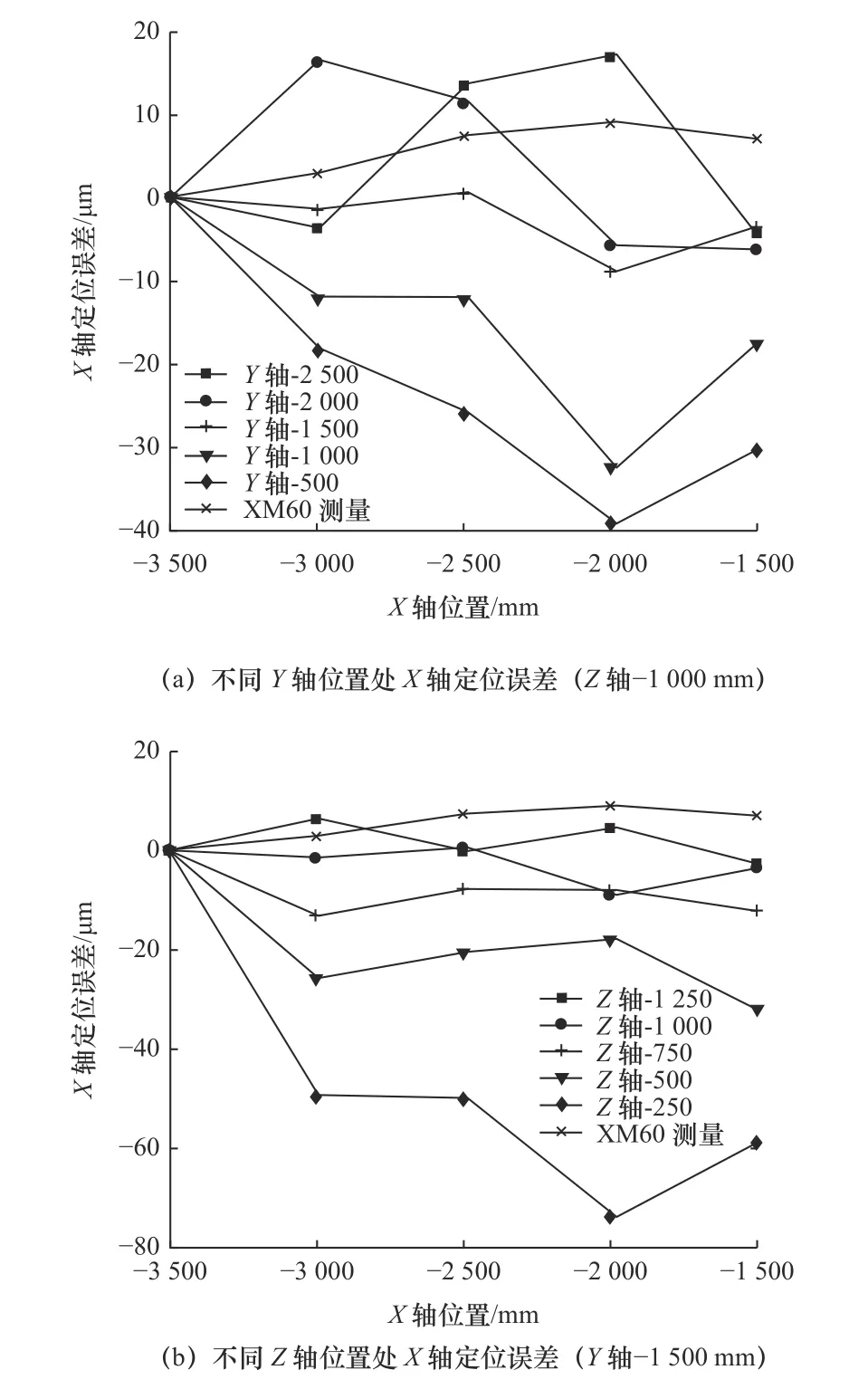
图5 不同位置处X 轴定位误差辨识结果

从图5a 可以看出，Z轴坐标为-1 000 mm，Y轴坐标在-2 500～-500 mm 内变化时，X轴定位误差变化范围为-39.2～16.8 μm。X轴在Y轴中间位置-1 500 mm 处定位误差最小，误差范围为-9.0～0 μm。这是由于该测量位置处存在支撑导轨，如图6 所示。龙门机床的立柱扭转也会导致刀具处反射镜位置随Y轴移动产生偏差，这亦会对X轴定位误差的测量结果造成影响。

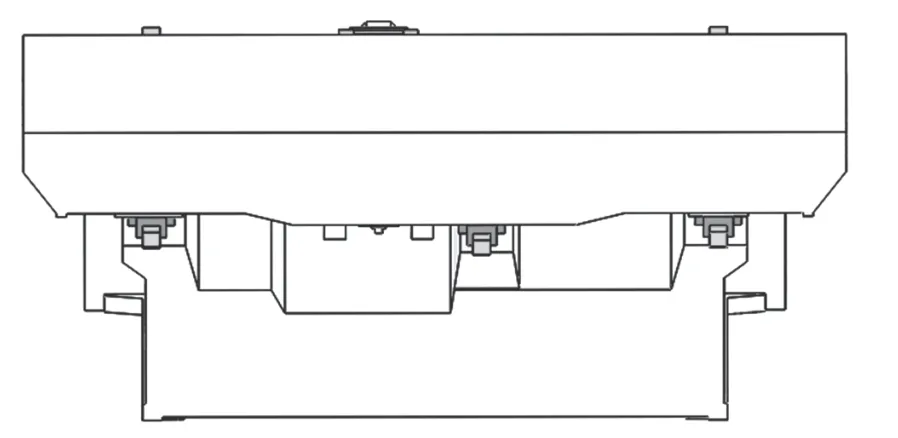
图6 工作台支导轨位置

Y轴坐标为-1 500 mm，Z轴坐标在-1 250～-250 mm 内变化时，X轴定位误差变化范围为-73.9～6.4 μm。随着Z轴升高，X轴的定位误差逐渐增大。主要原因在于存在与X轴空间误差相关的角度误差。Z轴位置升高，导致角度误差引起的阿贝误差增大，从而影响了X轴的定位误差。当Z轴升至-250 mm 位置时定位误差最大，最大值为-73.9 μm。

利用2.2 节所述方法得到工作空间内的体对角线误差，如图7 所示。

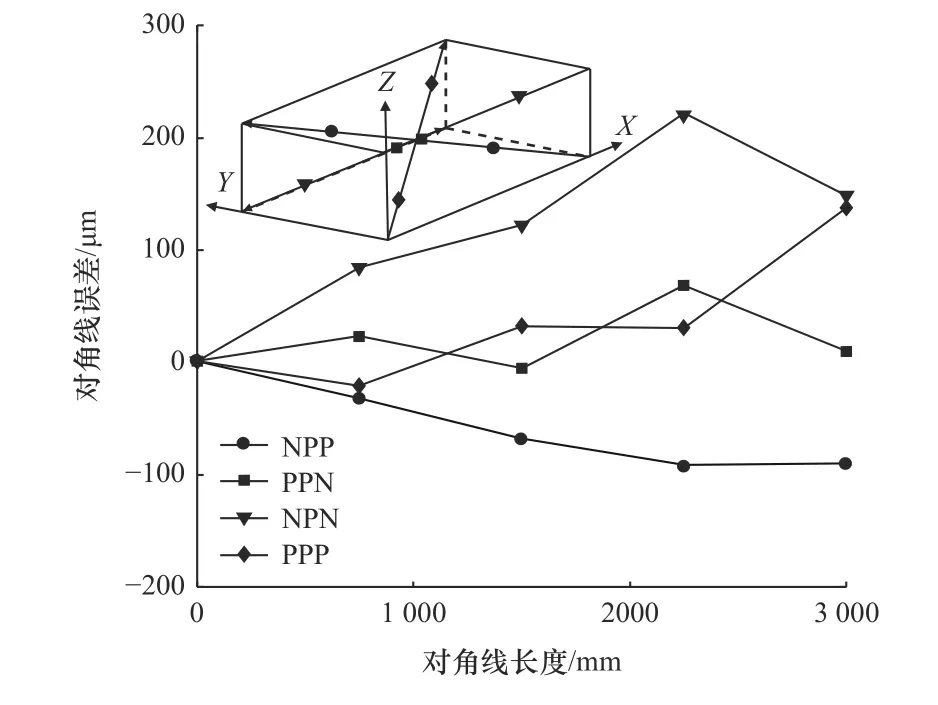
图7 空间体对角线误差

空间体对角线沿NPP 方向逐渐缩短，最大缩短值为94.2 μm。而在PPN 和PPP 方向均存在伸长趋势，最大值分别为67.7 μm 和136.6 μm。体对角线在NPN 方向上存在明显伸长，其最大值为219.6 μm。PPN 和NPN 方向对角线均在靠近工作台面时明显缩短，表明机床靠近工作台面处的精度较好，与图5b 分析结果吻合。

4 结语

传统测量方法难以获得直线轴在不同空间位置处的定位误差，且测量空间体对角线的光路调整较为繁琐。为此，本文提出了考虑空间位置差异的三轴机床多轴定位误差快速辨识方法。相较于现有方法，该方法可快速辨识直线轴在不同空间位置处的定位误差；同时避免了体对角线测量时的复杂光路调整，从而有效提高了测量效率。

利用所提出方法辨识龙门机床的定位误差及体对角线误差。以X轴为例，不同Y轴位置处最优定位误差波动范围为-9.0～0 μm，而最大定位误差波动范围为-39.2～0 μm，与多维激光干涉仪测量结果差异明显；究其原因，工作台支撑结构刚度及立柱扭转等因素可能对不同位置处的X轴定位精度产生影响。不同Z轴位置处的最优定位误差波动范围为-2.7～6.4 μm。而最大定位误差波动则为-73.9～0 μm，其主要原因为阿贝误差效应，Z轴升高导致X轴定位误差被放大。此外，空间体对角线在不同方向上存在明显的伸长与缩短差异。体对角线最大缩短值为94.2 μm，而最大伸长值为219.6 μm，表明机床空间精度的不均匀性。因此，为了有效预测机床的加工精度，必须考虑不同工作空间位置处的精度差异。

未来将进一步探究阿贝误差和机床安装误差等对于直线轴定位误差及空间误差的影响机制，形成客观表征机床直线轴真实误差的方法。