基于模糊一致矩阵的模糊综合评价法测评隐性知识存量

张驰庚 邱奕超

DOI：10.19850/j.cnki.2096-4706.2024.02.041

收稿日期：2023-08-17

基金项目：浙江省人力资源和社会保障厅、浙江省职业教育社科研项目（ZJCV2022C37）

摘  要：隐性知识存量测评是对当前学校考核评估教师教科研能力仅测评教师显性知识的完善。文章基于模糊一致矩阵的模糊综合评价法，研究教师隐性知识存量测评，包括：教师的隐性知识分类、建立评价问题指标体系，运用模糊一致矩阵配置指标权重、选择评价相关集、建立模糊综合评价模型，以及测评隐性知识存量，并实证分析高职教师隐性知识存量的测评过程。

关键词：高职教师；隐性知识；模糊一致矩阵；模糊综合评价；实证分析

中图分类号：TP391；G202    文獻标识码：A  文章编号：2096-4706（2024）02-0191-05

Evaluation of Tacit Knowledge Stock by Fuzzy Comprehensive Evaluation Method Based on Fuzzy Consistent Matrix

—Empirical Analysis of the Evaluation of Tacit Knowledge Stock of Higher Vocational Teachers

ZHANG Chigeng， QIU Yichao

（Jiaxing Vocational and Technical College， Jiaxing  314036， China）

Abstract： The evaluation of teachers' teaching and scientific research ability only assesses the explicit knowledge of teachers in current school， and the evaluation of tacit knowledge stock is the perfection for it. Based on the fuzzy comprehensive evaluation method of fuzzy consistent matrix， this paper studies the evaluation of teachers' tacit knowledge stock， including the classification of teachers' tacit knowledge， the establishment of problem evaluation index system， the allocation of index weights by using fuzzy consistent matrix， the selection of evaluation correlation sets， the establishment of fuzzy comprehensive evaluation model， and the evaluation of tacit knowledge stock. And it carries out the empirical analysis of the evaluation process of teachers' tacit knowledge stock in higher vocational colleges.

Keywords： higher vocational teacher; tacit knowledge; fuzzy consistent matrix; fuzzy comprehensive evaluation; empirical analysis

0  引  言

基于教育信息技术理念、运用多媒体技术，完善专业知识、有效完成教科研活动，达成教科研目标是教师须具备的职业能力[1]。这种能力具体体现在教师的显性知识和隐性知识两方面，如广博的教育信息技术知识、娴熟的教学技能、自我反思、创新能力、情感、意志发展等。对于教师掌握的显性知识能力，学校可采用学生成绩、科研成果、教师培训考核等方法评估；而教师掌握教育信息技术的诀窍、教学反思、创新能力及情感等隐性知识测评比较困难，因此很难评估教师的隐性知识量。本研究厘定高职教师隐性知识的分类，基于模糊一致矩阵的模糊综合评价法，研究高职教师隐性知识存量测评并作出实证分析。

1  高职教师的隐性知识分类

隐性知识与显性知识组成了人类的全部知识[2]。不同于具有可编码、可表述等特征的显性知识，隐性知识依附于个体，不可编码、难于表述。因此，对隐性知识有效分类有助于隐性知识的测评。关于隐性知识分类有多种方法，如野中郁次郞的隐性知识二分类：1）技能型。如手艺、操作诀窍等；2）认知型。如价值观、心智模式等；又如英国Eraut教授的三分类法[3]。经文献分析，本研究参照李作学教授的五分类法[4]：专业技能、人际关系、元认知、情感、价值观类，并将五分类法作为高职教师隐性知识的分类，如表1所示。

2  基于模糊一致矩阵的模糊综合评价法步骤

模糊一致矩阵[5]的模糊综合评价法[6]分成二大步：1）建立评价问题指标体系，运用模糊一致矩阵配置各指标权重；2）选择评价相关集，建立模糊综合评价模型[7]，测评隐性知识存量。

2.1  建立评价问题指标体系运用模糊一致矩阵配置指标权重

1）建立评价问题指标体系。将评价的目标和考虑的指标，按相互关系形成自上而下的层次。目标层（要解决的问题）；一级指标（因素层），二级指标（子因素层）。若有需要，可增加层次。

2）建立优先关系矩阵。矩阵Q = （qij）n×n，若0≤qij≤1，i，j ∈ Ω = {1，2，…，n}，称Q是模糊矩阵；若模糊矩阵Q满足qij + qji = 1，i，j ∈ Ω，称Q是模糊互补矩阵；设元素a1，a2，…，an两两比较重要程度的模糊互补矩阵为Q = （qij）n×n，若 ，qij = 0.5，表示相对上一层因素ai与因素aj同样重要；

qij = 0表示相对上一层，因素aj比ai重要；qij = 1表示相对上一层因素ai比aj重要，此时建立的Q = （qij）n×n称为优先关系矩阵。

3）优先关系矩阵转化成模糊一致矩阵。对优先关系矩阵按行求和，记为 ，i = 1，2，…，n，令rij = ，则R = （rij）n×n为模糊一致矩阵[8，9]。

4）各指标权重配置。用行和归一化得排序向量ω = （ω1，ω2，…，ωn）T，其中指标的各权重为：ωi = ，，，n为矩阵阶数。

2.2  选择评价相关集建立模糊综合评价模型测评隐性知识

1）选择评价相关集。评价事物涉及多个指标，需要综合多个评价主体参与，因此要确定评价主体集合；此外，选择与评价事物相关的其他集合。评价主体对评价指标评价过程中，需建立评价矩阵。

2）建立模糊综合评价模型，测评隐性知识存量。建立若干单因素评价矩阵分别与对应权重向量合成[7]，可得模糊综合评价模型，依据模型测评隐性知识存量。

3  高职教师隐性知识存量测评实证分析

3.1  建立评价问题指标体系及各指标权重配置

1）建立评价问题层次结构。根据表1教师隐性知识分类，建立评价指标体系，如表2所示。

目标层P：教师个体隐性知识存量。5个一级指标Fi，其权重ωi，i = 1，2，…，5；二级指标Fij，权重γij，i = 1，2，…，5；0≤j≤5。为省篇幅，表2已给出各指标权重，以下给出计算过程。

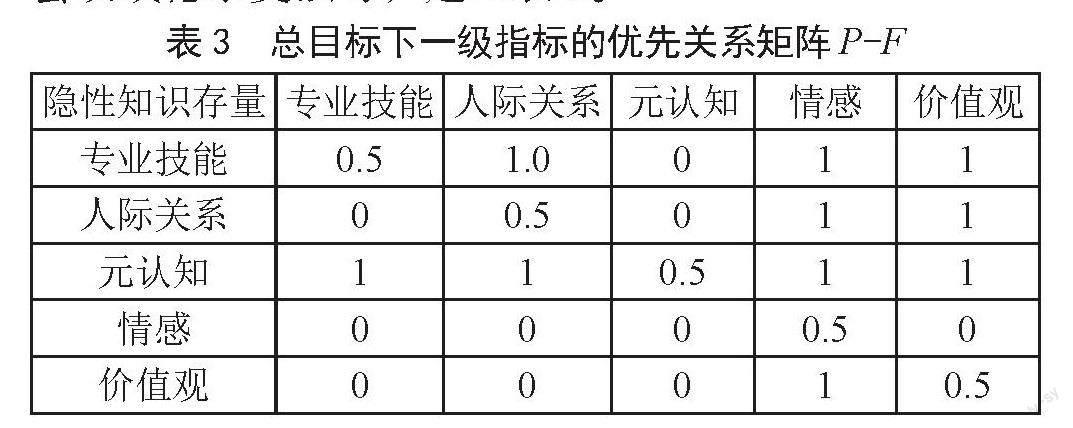
2）建立优选关系矩阵P-F。按步骤2，采取专家会议或德尔斐法等，建立表3。

3）优先关系矩阵P-F转换为模糊一致矩阵P-F。按步骤3，可得表4。

4）各指标权重配置。计算模糊一致矩阵P-F确定指标权重ωi，i = 1，2，…，5，如表5所示。

同理可得二级指标权重。例如，由表4中F1“专业技能”下F1j =（技艺、操作诀窍、动作准确灵活）的模糊一致矩阵F1-F1j，由此可得二级指标F1j权重向量（γ11，γ12，γ13，γ14）T = （3.0，3.0，2.5，1.5）T；由F1-F1j，i = 1，2，…，5；0≤j≤5，得其他四个二级指标权重。

3.2  建立模糊綜合评价模型测评隐性知识存量

3.2.1  选择相关集合建立评价矩阵

1）评价主体。客观、全面评价高职教师隐性知识存量，需多个评价主体参与。包括：教学督导组V1、同事V2间的评价，学生V3对任课教师评价，被评教师V4的自评，以及领导V5的评价。不同评价内容，评价主体的选择是不同的。例如，学生主体可参与对任课教师教学活动内容评价，但对教师科研活动不了解则不参与评价。

2）与评价相关的各类集。令专业技能、人际关系、元认知能力等评价指标为F，则评价指标集F = {F1，F2，…，F5}，令评语等级集为W，则W = {W1，W2，…，Wn}，本实例W = {优，良，中，差}。令所有评价主体构成的集V，则V ={V1，V2，…，V5}；

3）建立评价矩阵。若V t（t = 1，2，…，5）对F1的二级指标F1i评价，i = 1，2，…，4，则可得V t对指标F1的评价矩阵[7]为 ，如式（1）所示：

（1）

其中  是在V t下对指标F1i给予评语等级Wj（ j = 1，2，3，4）的隶属度[10]，如式（2）所示：

（2）

若V ={V1，V2，…，V5}，即所有评价人员对F1i给评语Wj（ j = 1，2，3，4）的隶属度，如式（3）所示：

（3）

则相应的评价矩阵为式（4）：

（4）

3.2.2  测评隐性知识存量

表6给出教师隐性知识存量评价指标体系、权重及单因素（单个虚线框）评价矩阵，评价组共20人构成，根据评价指标对教师个体Y，Z的隐性知识存量进行测评。

以教师Y为例，据表6，有5个评价矩阵A（A1，A2，A3，A4，A5），即单因素综合测评矩阵为：

其中γ1 = [γ11，γ12，γ13，γ14]T为二级指标[F11，F12，F13，F14]对应的权重。同理可得  = [0.29，0.44，0.22，0.05]， = [0.36，0.46，0.14，0.04]， = [0.47，0.37，0.13，0.03]， = [0.45，0.35，0.2，0]。

利用G1，G2，G3，G4，G5构建基于评价因素集F = {F1，F2，…，F5}的综合测评矩阵如下式GY。其中ω = [ω1，ω2，ω3，ω4，ω5]T，G由G1，G2，G3，G4，G5构成。同理，可得教师Z的隐性知识存量测评矩阵：H1 = γ1B1 = [0.36，0.54，0.1，0]，H2 = [0.37，0.49，0.14，0]，H3 = [0.48，0.32，0.2，0]。

H4 = [0.46，0.29，0.25，0]，H5 = [0.49，0.43，0.08，0]。类似GY可得GZ：

结果表明，教师Z的隐性知识存量水平高于教师Y。为更直观反映两位教师拥有的隐性知识存量，我们可以将{优、良，一般，差}用百分数表达：LT = {95，80，65，45}，则教师X的隐性知识存量测评得分PY = GY L = 82.10分；教师Z的得分PZ = GZ L = 84.20分；即PZ＞PY。

4  Python程序设计

隶属度、矩阵运算等计算，可设计Python程序[11]加以解决，编程框图如图1所示。

程序概略如下，其中传递的函数参数均为矩阵：

import  tensorflow  as  tf

def  matrix_1（x1，x2，…，xn）：

…………………………

result = tf.matmul（x1，x2）

return  result

…………………………

def  matrix_2（y1，y2，…，ys）：

…………………………

def  evaluation_results （……）：

…………………………

if __name__=="__main__"：

x1 = [[x11， x12，…，x1m]， [x21， x22，…，x2m]，…， [xk1，xk2，…，xkm]]，

x2= [[x11， x12，…，x1p]， [x21， x22，…，x2p]， …， [xm1， xm2，…xmp]]，

…，matrix_1（x1，x2， …，xn），… ， y1=[…]， y2=[…]， … ， ys=[…]，

matrix_2（y1，y2，…， ys）， …。

5  結  论

借助优先关系矩阵构造模糊一致矩阵，使传统的层次分析判断一致性存在的问题得到解决，从而使教师的隐性知识存量测评更为科学合理。此外，评价主体对教师个体隐性知识存量评价过程是不可或缺的，其余烦琐计算，可通过设计Python程序一次性解决。

参考文献：

[1] 刘家良，于胜刚.高校教师个体教学能力发展路径探析 [J].中国成人教育，2016（11）：152-154.

[2] Polanyi M.The Study of Man [M].Chicago：The University of Chicago Press，1958：12.

[3] 黄荣怀，郑兰琴.隐性知识论 [M].长沙：湖南师范大学出版社，2007：46.

[4] 李作学.隐性知识计量与管理 [M].大连：大连理工大学出版社，2008：138-195.

[5] 王领元，王晓燕.基于模糊一致矩阵的模糊层次分析法在锚地优选方案中的应用 [J].中国水运：下半月，2016，16（10）：217-218.

[6] 杨靖，王震，杨双琪，刘志国.大学隐性知识管理研究 [M].保定：河北大学出版社，2015：231-242.

[7] 杜栋，庞庆华，吴炎.现代综合评价方法与案例精选 [M].北京：清华大学出版社，2015：43-45.

[8] 徐泽水.模糊互补判断矩阵排序的一种算法 [J].系统工程学报，2001（4）：311-314.

[9] 陶余会.如何构造模糊层次分析法中模糊一致判断矩阵 [J].四川师范学院学报：自然科学版，2002（3）：282-285.

[10] 谢季坚，刘承平.模糊数学方法及应用 [M].武汉：华中科技大学出版社，2013.

[11] 龙良曲，盛东亮，钟志芳.TensorFlow深度学习 [M].北京：清华大学出版社，2020;51-85.

作者简介：张驰庚（1984—），男，汉族，浙江杭州人，讲师，硕士，研究方向：数据挖掘、教育管理；邱奕超（1989—），男，汉族，浙江嘉兴人，工程师，硕士研究生，主要研究方向：计算机应用技术。