黑猩猩算法优化光伏MPPT的研究
王宛阳,朱立颖,张 明,张文佳,童乔凌
(1.华中科技大学集成电路学院,湖北武汉 430074;2.北京空间飞行器总体设计部,北京 100094)
光伏发电是一种清洁能源手段,具有十分广阔的应用场景,将是未来月球科研站分布式能源系统的基础组成模块[1]。为了充分地利用光能,光伏电池应当工作在最大功率点。为此后级DC/DC 变换器需要根据工况进行不断调节,这一过程被称为最大功率追踪(maximum power point tracking,MPPT)。MPPT 的速度和精度对光伏发电量具有重要影响,其控制方法得到广泛研究[2-3]。
MPPT 的常规方法有固定电压法、扰动观察法、电导增量法、短路电流法等[4-6]。其中,固定电压法不适合于具有温度变化的场合[4]。电导增量法作为扰动观察法(perturb and observe,P&O)的改进,具有更准确和快速的响应,但其步长设置无法兼顾速度与精度[5]。短路电流法会引入短路电流脉冲,造成系统的扰动和功率损失[6]。
为了克服这些常规方法的缺点,改进的MPPT算法被提出。其中,引入变步长的MPPT 算法平衡了速度和精度的矛盾,但其建模较为困难且硬件精度要求高[7-8]。进一步引入智能算法的MPPT 算法,不需要建模,具有自适应能力,但需要一定训练过程。智能算法中基于模糊逻辑(fuzzy logic,FL)控制的算法相比基于人工智能网络(artificial neural network,ANN)的算法具有成本更低、易于理解、易于实现的优点,常与其它控制方法结合,以改善系统的追踪速度和精度[9-11]。
基于FL 的MPPT 算法可以进一步优化。通过改变模糊逻辑控制器输入输出函数,以单独或不同组合的优化算法调整成员隶属度函数(membership function,MF)参数,可提高其追踪性能。遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)以及蚁、蜂、鲸群等优化算法在过去被应用[12-16]。Khishe 和Mosavi 在2020 年提出一种黑猩猩优化算法(chimp optimization algorithm,ChOA),具有搜索更准确、搜索时间更短等优势,但其在MPPT 上的应用尚缺乏研究[17-19]。
本文提出一种基于黑猩猩算法优化的MPPT 方法。采用由七三角形MF 组成的非对称模糊逻辑控制器,与扰动观察结合实现MPPT。利用黑猩猩方法迭代提高搜索精度减少搜索时间。在优化过程中,适应度函数是成本函数在不同辐照和温度工况下的加权和,而成本函数通过各工况下的暂态和稳态指标建立。通过MATLAB/Simulink 仿真验证了该MPPT 方法在不同光照条件下均有较好的追踪速度和精度。
1 黑猩猩优化算法
1.1 算法思想
黑猩猩优化算法是根据黑猩猩群体狩猎行为提出的一种元启发式算法。在黑猩猩群狩取猎物的过程中,其成员具有不同的分工,并采取不同的策略协助狩猎,其群体分工还会随着时间推移变化。基于此,算法引入四种典型黑猩猩:攻击者(attacker)、追捕者(chaser)、拦截者(barrier)、指挥者(driver),它们由群体中狩猎收获的评分最高的个体担任。它们采用四个不同策略追踪猎物位置,群体将根据它们的追踪向猎物位置移动。而另一方面,群体移动时会进行分散,并可能根据社会动机设定,进行随机混沌移动。这样可以更快地找到猎物并避免丢失潜在的更优质猎物。
1.2 算法数学描述
算法的数学描述如下:
首先描述追踪猎物的行为。假设一只进行追踪的黑猩猩在N维空间中某一时刻的位置向量为Xchimp(t),而预测的猎物位置向量为Xprey(t),其在下一时刻的位置将为:
式 中:a、m、c为系数向量,a=2fr1-f,c=2r2,m=Chaotic_value(基于混沌映射的混沌向量)。r1和r2是取值范围为[0,1]的随机向量,f为设定的收敛因子,一般随迭代次数t增加非线性下降到零。
a是表征黑猩猩移动受猎物位置的影响程度的向量,当|a|>1 时,黑猩猩被迫分散远离猎物,当|a|<1时,黑猩猩聚拢靠近猎物。c是一个表征黑猩猩猎物位置对黑猩猩狩猎影响的随机权重量,当c>1,猎物位置的影响加强,当c<1,影响减弱。m是一个混沌因子,表征混沌移动的影响。
黑猩猩个体根据群体追踪行为移动。每只黑猩猩根据当前的attacker、chaser、barrier、driver 的追踪行为进行移动。其表示为:
如前所述,黑猩猩可能根据社会动机(性或装饰)进行混沌移动,这一行为通过数学描述为:
式中:μ为取值范围为[0,1]的随机数。在求解高维问题时,混沌移动帮助解决陷入局部最优和收敛速度慢等问题。
2 光伏MPPT 系统模型
2.1 月面光伏的应用场景
为了综合开发利用月球资源,将在2030 年前后,以已展开的月球探测为基础,探索建造月球科研站。科研站将配套光伏电池保障能源供应[1]。在该场景下的光伏应用具有新的特性。
在位置选择上,现阶段月球科研站最可能的选址,一般被认为在接近月球南北极的陨石坑。这些位置独有的优势包括:南北极位置因极昼现象具有的稳定不间断光照时间更多、昼夜温度的波动更小、矿物资源丰富含有水冰、陨石坑边缘山体能提供不易被遮挡的通信角度等[20]。
在这些高纬度位置,不考虑地形的情况下,理想的光照几何关系如图1 所示。
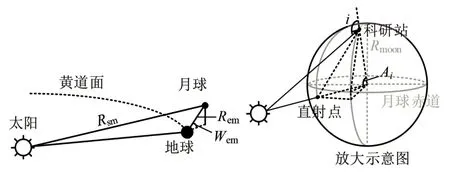
图1 月球科研站光照情况
忽略天体和尘埃的反射散射造成的能量衰减,根据入射角估算辐照的公式为:
式中:i为观测点的入射角,由Ai和直射点、科研站的经纬度根据几何关系决定;S0为太阳常数;Wem为月球的地心黄纬;Rem为地月距离;Rse为日月距离。
以惠普尔陨石坑位置为例,其位于北纬89.14°、东经120.02°,假设第0 天月球位于天球春风点并为升交点,当地球全年在近日点和远日点之间运动时,其辐照度随时间变化的估计曲线如图2 所示[21]。
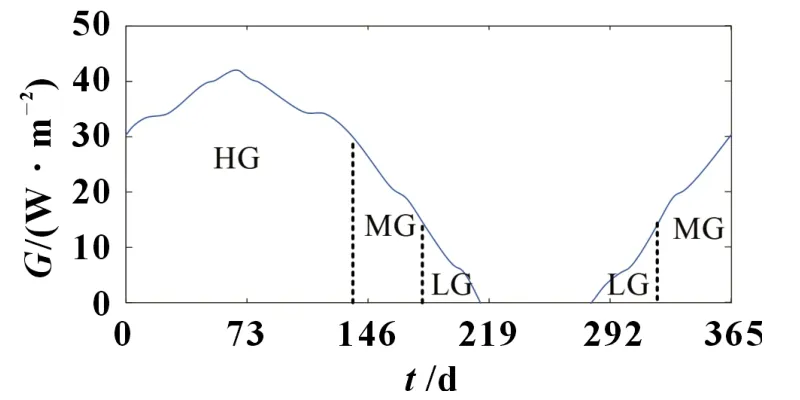
图2 惠普尔坑位置的辐照估计
根据辐照估计曲线,对于与平坦月球面平行放置的光伏电池,光照条件可划分为图示的低光照(LG)、中光照(MG)、高光照(HG)三个区段。对于一般的GaAs/Si 光伏电池,100 W/m2以下的极弱光强难以发电。因此在空间领域,多采用(GaInP/GaAs/Ge)三结GaAs光伏电池。此类电池能在极低光照、低温、高辐照的情况下工作,经过“金星快车”金星探测器、“朱诺”木星探测器、“深空1 号”等探测器的验证[22-23]。其中木星距太阳5.2 AU,光照强度在100 W/m2以下,土星距地球9.54 AU,光照强度约在10 W/m2。对于温度条件,惠普尔坑附近的准永久光照区域温度较稳定,为(-50±10) ℃[20],可假定温度为-50 ℃简化分析。此外,利用地形和机械控制,可使光伏电池倾斜于平坦月球面工作。理论上最大可获得约等同于地球距离的垂直光照强度。本研究以MPPT 控制为主,不再深入电池倾斜控制,后续以假定光照条件进行研究。
2.2 光伏系统仿真模型
系统仿真模型包括光伏电池组、Boost 变换器、最大功率追踪模糊控制器。在Simulink 搭建,如图3所示。
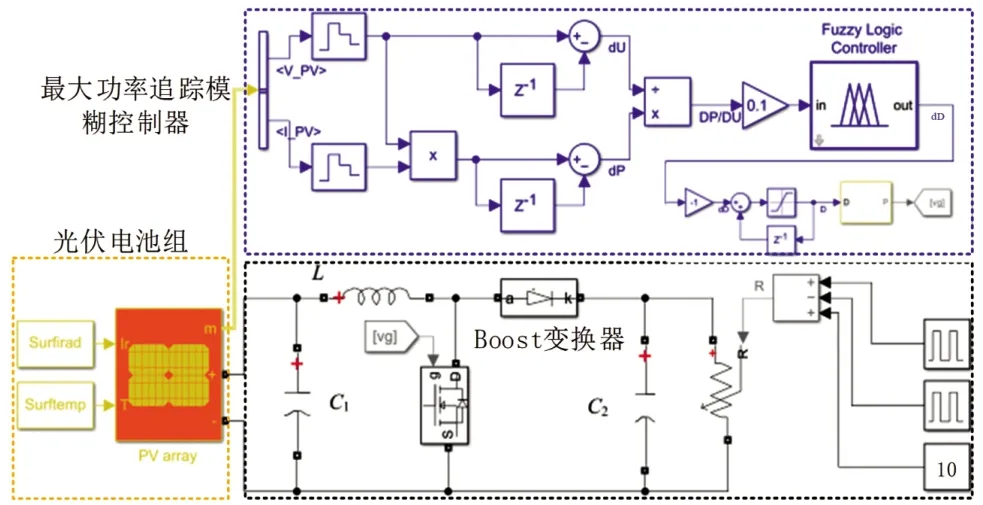
图3 系统仿真模型
Boost 变换器的主要参数为:L=200 μH、C1=100 μF、C2=400 μF、R=10 Ω,R在仿真中设置20%的正负跳变,控制频率为100 kHz,P&O 调节占空比步长为0.001 和0.003。
光伏电池型号采用ASEC140G6M,光伏电池的基本特性方程为:
式中:Isc表示光伏电池在标准测试条件下(G=1 000 W/m2,温度为25 ℃)下的短路电流;Tref为标准参考温度,K;CT为温度补偿系数;I0为反向饱和电流;n为光伏电池p-n 结的理想因子;k为玻尔兹曼常数;q为单位电荷量;Rsh和Rs为并联漏电阻和引线电阻。电池组采用6 串12 并,代入电池数据和2.1 节确定的G和T,绘制电池组的I-V和P-V特性如图4 所示。
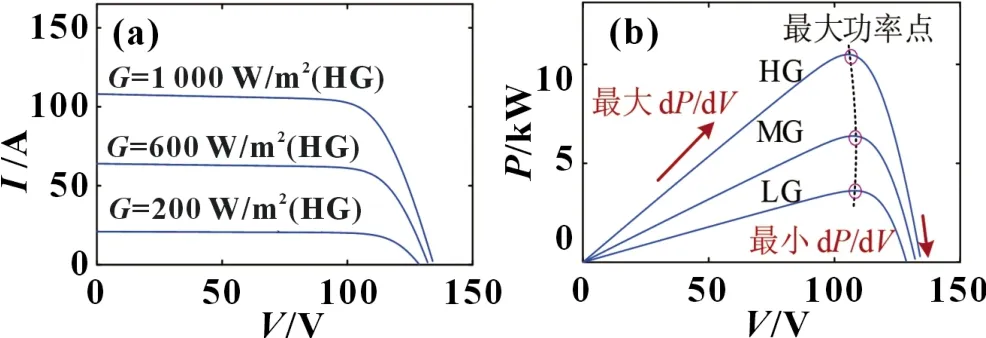
图4 在-50 ℃下电池组的I-V和P-V特性
假定太阳电池经过倾斜控制,具有的光照强度G可划分为200、600、1 000 W/m2,分别体现低光照条件(LG)、中光照条件(MG)、高光照条件(HG)下的I-V和P-V特性。MPPT 控制需要在多个光照条件下尽可能准确追踪避免功率损失。
2.3 非对称模糊逻辑控制器
模糊逻辑控制器搭建的难点之一是依赖于经验。为了解决这一问题,提供一种基于dP/dV特性的非对称模糊逻辑控制器设置方法。
首先,dP/dV在扰动观察法中可以作为MPPT 的控制依据,而如图4 所示在给定条件下dP/dV具有量化的最大最小值,因此采用dP/dV作为模糊控制器的单输入。在G=1 000 W/m2时,max(dP/dV)=100.8 W/V,min(dP/dV)=-1 006 W/V,考虑余量和缩放,模糊控制器输入范围确定为[-120,12]。
其次,光伏阵列的P-V特性在MPPT 点左侧和右侧具有非对称的特点,在左侧dP/dV始终大于0,而右侧dP/dV始终小于0。因此,将模糊控制器输入隶属度函数进行非对称设置,能够更好地对不同情况进行分辨和调节。最后,采用七三角形隶属度函数的模糊控制器往往能在隶属度函数数量和瞬态稳态性能间取得最好的平衡[24]。
控制器的设置如图5 和表1 所示,在非对称的基础上,dP/dV的输入三角形隶属度函数按照x1=x2=x3=|min(dP/dV)|/3,x4=x5=x6=max(dP/dV)/3 进行初始化设置,ΔV的输出隶属度函数采用对称设置。这种设置方法有助于保持模糊逻辑规则的简单性。当dP/dV隶属负大(NB)时,工作点靠近P-V曲线的最右端,这对应着输出隶属负大(NB),从而快速增加D。在成员名称中,N 表示负、P 表示正,B、M、S 分别代表大中小,ZE 代表零。至于x1至x6,在接下来通过黑猩猩算法进一步优化。

表1 模糊逻辑规则
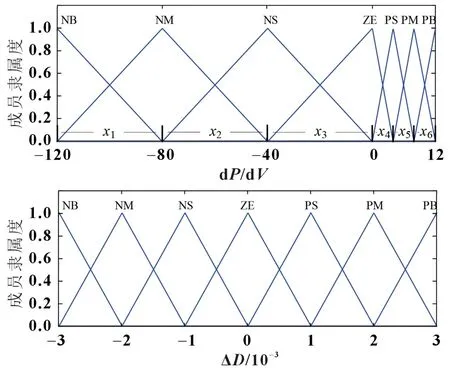
图5 输入dP/dV和输出ΔD的成员隶属度函数
3 优化方法
3.1 适应度函数
控制器的优化目标是MPPT 的速度和精度,为此提出相应评估方法。假设当前光照和温度电池组最大功率为Pm,大于上升时间的时间窗口为Tw,上升时间tr定义为首个[tr,tr+Tw]期间P(t)>0.9Pm且持续时长大于Tw的时间点,MPPT 的速度采用上升时间评估。而理想的MPPT 在给定时间窗口(Tw)中产生的能量为E=PmTw,精度通过产生的能量与E的差值评估。成本评估函数建立为:
式中:tr0为采用未优化的控制器参数时的上升时间;tend为仿真结束时间;0.3 和99.7 是加权系数。月面高真空状态光照变化很稳定,调节速度相对次要,对精度的权重进行了提升。
控制器参数优化需要兼顾多个工况,但应当有所侧重保证整体效果最优。假设光伏电池组一年中可能的光照强度如图6 所示。用days(i)表示第i种光强的工况在一年中出现的天数,则通过光照强度划分的第i种工况的情况下,确定其加权系数为:

图6 假定的光伏电池组一年中的光照强度
基于式(6)和式(7)最终建立适应度函数如下:
本文中对应LG、MG、HG 条件确定的加权系数为w(1)=0.277,w(2)=0.515,w(3)=0.208。
3.2 优化流程
虽然ChOA 算法具有较快的收敛速度和精度,但其算法搜索能力和收敛性能仍与迭代中采取的策略相关。为此,引入规则加快收敛。
首先,限制优化量:
其次,根据非对称性和dP/dV范围量化设置收敛因子。设当前迭代次数为niter,最大迭代次数为Niter,非线性收敛因子表示为:
其中对x1、x2、x3适用f0=|min(dP/dV)|/5,对x4、x5、x6适用f0=max(dP/dV)/5。以x1、x2、x3为例,其收敛因子曲线如图7 所示,体现不同黑猩猩角色以不同的策略对探索和开发进行了平衡。
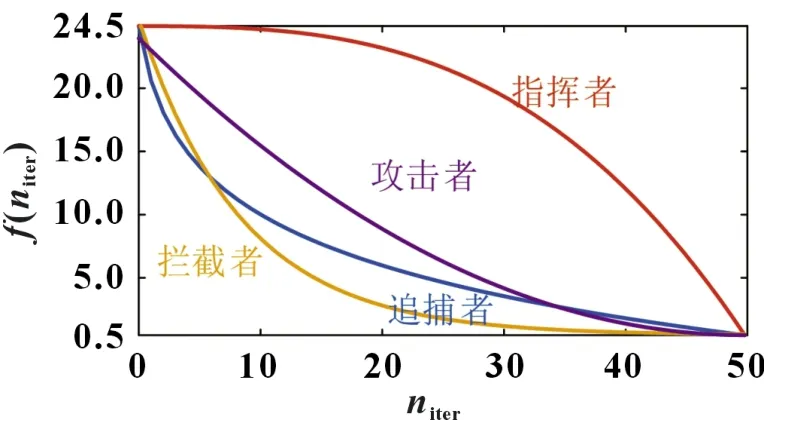
图7 Niter=50时x1、x2、x3的收敛规则
最后,整个算法流程为:
Step1 参数初始化,本文种群数(搜索代理数量)为50,最大迭代次数为50。
Step2 随机初始化黑猩猩种群位置,采用Iteration[xn+1=sin(bπ/xn)]映射生成m,b取0.7。
Step3 开始第niter次迭代,依次遍历种群。
Step4 规则检查,对违规位置进行缩放限制。
Step5 适应度函数计算(调用仿真)。
Step6 更新attacker、chaser、barrier、driver。
Step7 更新f、a、c、m,计算并更新个体每个维度的位置。
Step8 判断循环是否结束,种群遍历后niter加一并返回第三步,满足迭代次数后记录attacker 位置并跳出循环。
算法流程图如图8 所示。
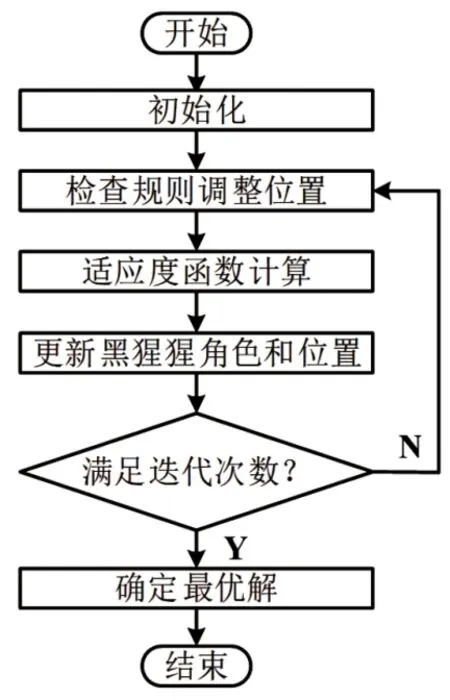
图8 黑猩猩算法流程图
4 优化和仿真结果
经过迭代后的控制器参数为:x1=11.747,x2=7.259,x3=8.617,x4=2.667,x5=8.733,x6=0.600,对应的隶属度函数如图9 所示。图10 给出了G=600 W/m2,温度为-50 ℃时不同步长的P&O 控制和优化前后模糊逻辑控制的功率追踪曲线。几种情况下的适应度函数和成本评估在表2 中给出。

表2 成本和适应度
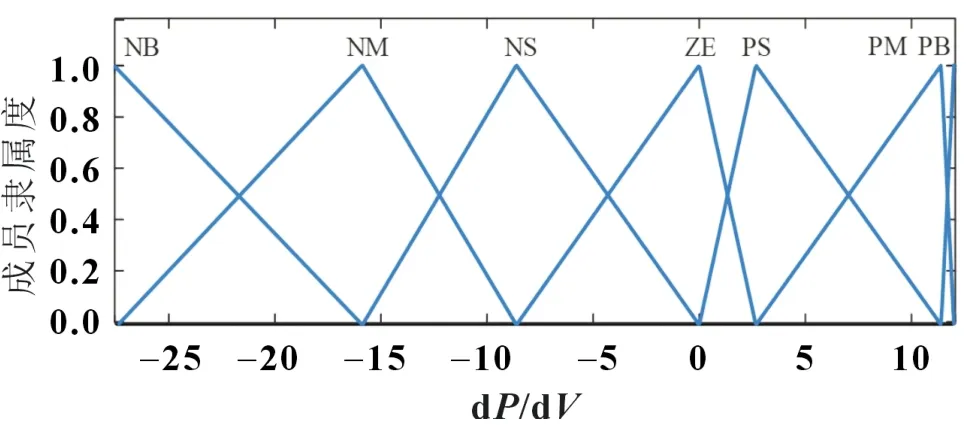
图9 优化后输入dP/dV的成员隶属度函数
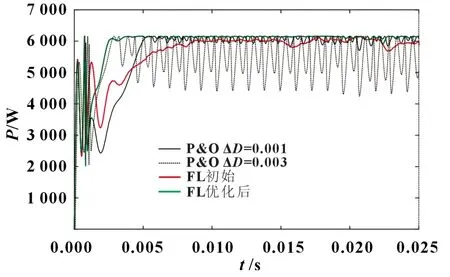
图10 G=600 W/m2,温度为-50 ℃时的仿真功率追踪曲线
对比之下,在G=600 W/m2,温度为-50 ℃时,采用本文黑猩猩算法优化后的MPPT 控制,上升时间相对ΔD=0.001 的P&O 控制减少了52%,上升速度优于ΔD=0.003 的P&O 控制,在存在频繁调节的情况下损失的效率更小。而在稳态窗口时间里的功率跟踪损失Eloss(Eloss=PmTw-Integral{V(t)I(t),tend-Tw,tend},tend=0.025,Tw=0.01)相 对ΔD=0.001 的P&O 控制和ΔD=0.003 的P&O 控制分别减少了82.2%和97.5%,等价于将效率分别提升1.4%和13.5%。
综合三种工况来看,本文控制获得最优的适应度值,具有最小的上升时间和最少的功率跟踪损失,提升了MPPT 的速度和精度,优化了光伏发电的效率。
5 结论
本文提出了黑猩猩算法优化光伏MPPT 应用的模型和方法。根据光伏电池特性方程,确定了电池组的关键P-V曲线。根据dP/dV在MPPT 点左侧和右侧非对称的特性,给出一种量化的非对称模糊逻辑控制器设置方法。建立了仿真系统模型,模型下相对同最大步长P&O 控制MPPT 追踪更快,稳态扰动更低。通过黑猩猩算法对MPPT 算法进行进一步优化,给出了适应度函数、优化规则、非线性收敛因子、算法流程等模型内容。最终优化后的MPPT 算法对比P&O 和优化前算法有效提升了MPPT 的速度和精度。

