基于PC老化行为的西藏大气环境严酷度预测

吴德权，覃 粒，谭甜甜，陈星昊，赵方超，张达威，杜翠薇

1) 西南技术工程研究所，重庆 400039 2) 北京科技大学腐蚀与防护中心，北京 100083

高分子材料老化是服役环境中光、热等多种环境因子共同作用的复杂过程[1]. 我国西藏地区由于海拔高、紫外线强烈，是高分子材料老化的“重灾区”. 一些在普通地区能够服役数十年的高分子材料，在西藏地区强紫外线作用下寿命能减少至数年[2]. 如萧以德等[3]早在2003年即呼吁装备设施建设过程中要充分重视西部地区高分子材料老化情况，并组织重大项目开展了西部地区材料服役调研. 杜武青[4]研究发现西部大气环境不饱和聚酯玻璃钢弯曲强度衰减速度是武汉的2倍. 刘俊[5]研究发现电网复合绝缘子在拉萨地区的臭氧及紫外线作用下老化速度远远大于福建等沿海地区；对于硅橡胶等耐候型橡胶，在拉萨暴露2年表面就出现粉化. 近年来，国家积极布局西部开发战略，西藏地区工程建设如川藏铁路、湘河水利工程等一系列重大设施，离不开高分子材料的选用. 如不重视高分子材料在西藏地区的老化失效，将造成巨大经济损失甚至不可估量的安全灾难.

为保障西藏地区装备设施中高分子材料安全服役，需充分掌握高分子材料在西藏各地环境适应性，对西藏地区大气环境严酷度深入了解，对高分子材料在西藏地区的老化行为进行预测. 因此，研究高分子材料在西藏地区老化行为时间及空间规律，提前掌握高分子材料在西藏各地老化差异，在装备设施服役前对大气环境严酷度提供预测预判，为装备正向设计与选材提供数据支撑，可以有效指导装备设施在特定时间及空间服役开展精准防护.

目前针对大气环境严酷度评估的研究，主要集中于大范围如全国地区严酷度评价，且主要集中于金属腐蚀大气环境严酷度评价研究[6]. 而高分子材料服役环境严酷度评价研究较少，尤其是针对局部服役地区大气环境的高分子材料老化严酷度精细量化评价更是鲜有报道[7-8]. 目前高分子材料西藏地区老化行为研究，主要集中于拉萨等少数几个站点，而对整个高原地区大气环境差异及材料老化行为差异研究较少. 如Liu等[9]及其团队通过在全国6个典型气候环境站点开展PC（聚碳酸酯）塑料暴露试验获得老化预测模型，虽然数据表明拉萨站PC老化程度较大，但该通用模型未能精细化预测西藏地区老化差异. 因为西藏地区海拔高，地广人稀，人员活动受空气中含氧量及地理因素限制，在西藏各地广泛开展自然暴露试验难度及成本极大. 另外，针对高分子材料的老化行为预测，关键在于建立材料失效与环境之间的映射模型，而国内外对高分子老化模型构建方法的研究主要集中在通过加速试验预测材料寿命[10-12]，或从材料老化机制角度探究其动力学过程[13-15]. 如Gillen等[16]研究了乙丙橡胶在不同温度下的老化性能之间的关联，通过高温老化试验预测橡胶在常温环境中的寿命；Sameshima等[17]研究了PC与橡胶室内热老化机制，通过设计热老化试验预测橡胶户外失效行为. 这些方法一般多用于预测特定设计人工环境或典型试验环境中的老化行为或寿命，然而模型普适性难以支撑其对实际服役环境进行精准量化评估. 如何预测高分子材料在户外实际复杂环境下的老化行为且具有普适性，则成为研究难点.

近年来，随着计算机及网络技术的发展，新型智能算法在建立材料行为模型方面逐渐应用[9,18].如Tesfamariam与Martín-Pérez[19]通过贝叶斯信念网络，建立了钢筋混凝土的碳化腐蚀模型，该模型可同时考虑6个变量对腐蚀的影响；Caleyo 等[20]和Ossai等[21]通过蒙特卡洛模拟建立了管线钢内壁的点蚀生长模型，预测精度相比于传统回归分析高出一倍；Xiang等[22]等通过训练BP（Back propagation，反向传播）神经网络较好地预测了橡胶在拉伸疲劳条件下的寿命；Kamrunnaha与Urquidi-Macdonald[23]通过合金成分与环境间的映射关系建立神经网络模型，预测了碳钢、钛等金属的腐蚀速率，预测结果与实际结果较吻合. 相比于传统基于老化动力学模型或实验探索方法，智能算法对材料老化机制并不需要深入了解，相反基于大量历史数据或同类别数据计算，其在数据容错纠偏方面有独特优势，在提高预测或评估模型准确性、普适性方面的优势逐渐凸显[24-27].

本项目组率先在西藏全域10个站点开展大规模自然暴露试验，通过采集PC老化数据及环境数据，基于机器学习等算法模型，建立了对西藏大部分气候环境具有普适性的高精度预测模型；通过向该模型输入西藏28个站点年均与逐月环境数据，预测了PC在西藏的28个站点老化值及逐月变化情况. 以PC色差年变化值为严酷度评价指标，绘制了西藏严酷度空间分布图并预警了老化严重地区. 基于环境逐月变化数据规律，预示了PC老化严酷度季节性变化规律. 该研究为西藏地区装备设施安全服役、高分子选材及防护提供了重要支撑.

1 试验方法与研究方法

1.1 PC材料西藏地区自然暴露试验

自然暴露试验按照GB/T 3681.2—2021在西藏10个城市的大气暴露试验站进行，时间为2021年4月至2022年4月，样品回收周期为3、6、9、12个月共4个周期，每周期回收色板试样、拉伸试样平行样品数量各为5个. 试样由四川大学青岛研究所加工制备，选用德国拜耳2865透明通用PC树脂，分别按照GB/T 17037.3—2003标准[28]、GB/T 1040.2—2022[29]标准尺寸要求注塑成型. 色板试样为符合GB/T 17037.3—2003[28]标准的方块试样（70 mm×50 mm×3 mm），用于表观性能测试；拉伸试样为符合GB/T 1040.2—2022[29]标准的1A型试样，用于力学性能测试. 10个站点位于拉萨、察隅、波密、林芝、昌都、拉孜、当雄、羊八井、班戈、那曲（图1），分布于西藏大部分地区及不同海拔高度.

图1 自然暴露试验过程. (a)西藏各地环境试验架；(b)站点位置图Fig.1 Environmental exposure tests: (a) the shelf for environmental tests in Tibet; (b) the locations of the stations

西藏是独特的高原气候，受地形、地貌和大气环流的影响，气候复杂多样. 所选10个站点涵盖了西藏典型区域及气候特征：以察隅、波密为代表的藏东南地区，受印度洋暖湿气流影响温和多雨；以昌都为代表的藏东北地区，地处横断山脉和三江流域，高原与季风气候特点明显，夏季温和湿润、冬季干燥寒冷；以拉萨为代表的藏中南地区，属高原河谷地形，降水稀少、气候干燥；以拉孜为代表的藏西南部多山地，具有日温差大、雨水集中、干湿分明的特点；那曲、班戈等藏北地区，位于羌塘高原东南侧，海拔高、空气稀薄、太阳辐射强，一定程度上可代表羌塘高原上广袤的无人区地带气候特征. 试验期间2021年4月至2022年4月，西藏各站点的气象数据年平均值如表1所示. 预测未投样地区所用大气环境数据由拉萨气象局提供，数据为2021年28个城市气象数据.

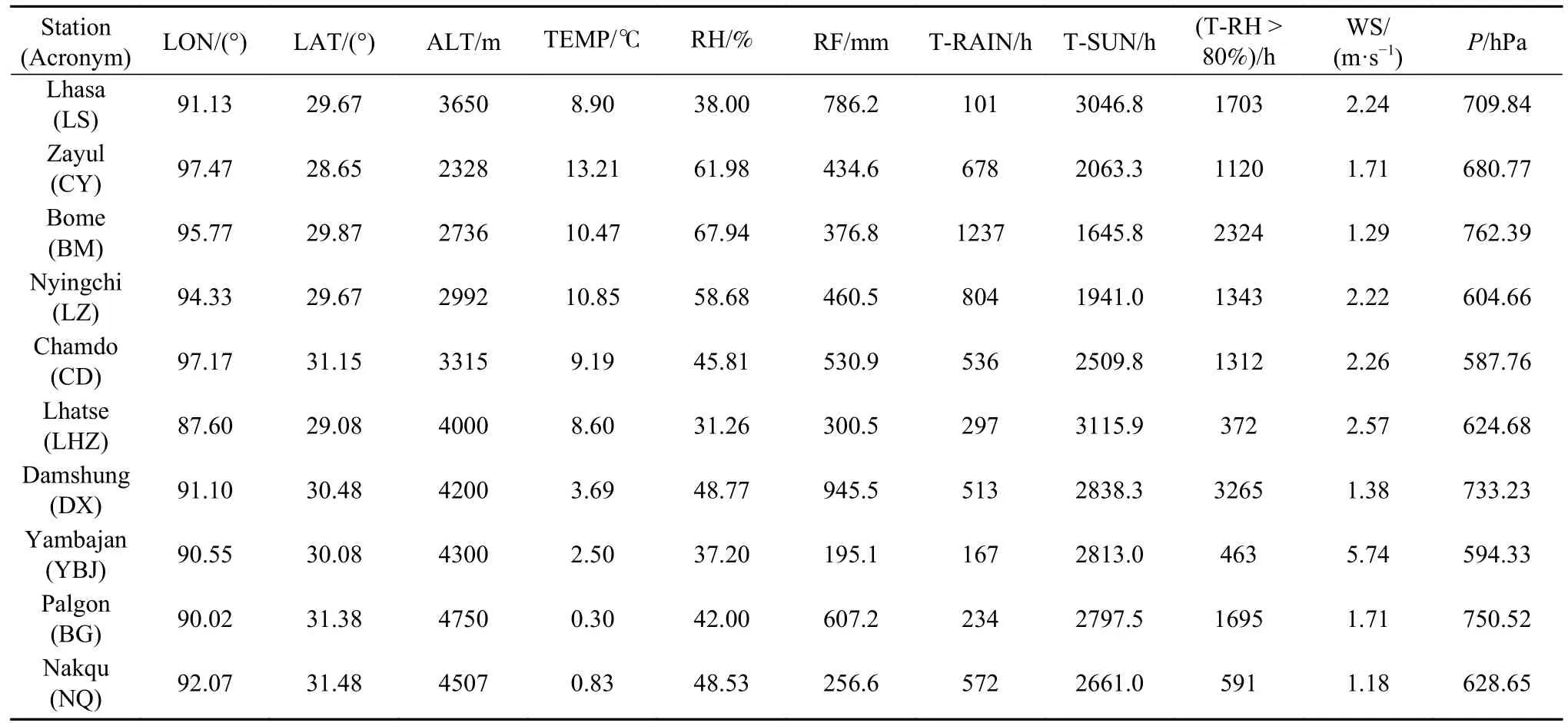
表1 西藏各站点气象数据Table 1 Climate data for the testing stations in Tibet

1.2 试验测试方法

1.2.1 色差测量

色差的计算依据GB/T 7921—2008[30]标准确定的操作步骤进行. 在D65光源下用分光光度计测量色板试样的L*，a*和b*，按公式（1）计算试样色差值：

其中，ΔE表示色差值，L*、a*和b*分别表示试样明度系数、红绿系数与黄蓝系数；L*0、a*0和b*0分别表示标准样明度系数、红绿系数与黄蓝系数. 色差值大小可用于评价PC的老化程度，色差值越大老化程度越高.

1.2.2 失光率测量

失光率是材料经老化后光泽度改变量与老化前光泽度的比值，计算过程如公式（2）可用于评价PC的老化程度.

其中，GL为失光率，A0为老化前材料表面光泽度，A1为老化后材料表面光泽度.

表面光泽度测量依据ASTM D523—2014[31]标准确定的操作步骤进行. 采用镜向光泽度计以85°入射角光线测量色板试样光泽度.

1.2.3 力学性能测试

通过拉伸试验开展力学性能测试，获得PC拉伸强度及拉伸断裂应变性能数据. 拉伸试验按照GB/T 1040.1—2018[32]标准确定的操作步骤进行.试样拉伸试验速度为5 mm·min-1满足试样能在0.5～5 min试验时间内断裂的最低速度. 拉伸强度按照公式（3）计算：

其中，σt为拉伸强度，p为最大载荷，b、d分别为试样的宽度与厚度. 拉伸断裂应变按照公式（4）计算：

其中，εt为拉伸断裂应变，G与G0分别为试样断裂时标距与试样原始标距. 拉伸强度与拉伸断裂应变是材料力学性能的重要指标，可用于评价PC老化程度.

1.3 数据计算方法

1.3.1 皮尔逊（Pearson）相关性分析

Pearson相关分析用于计算气候因素之间的相关性，其计算过程如公式（5）所示. 相关性系数r描述两个变量之间的线性相关程度.r的值在-1和+1之间. 如果r>0，表明两个变量正相关；r＜0，则表示两变量负相关.r的绝对值越大，相关性越强.

其中，r表示相关性系数，Xi，Yi分别表示两个变量，分别表示两个变量均值.

1.3.2 灰色关联度分析

灰色关联度分析是根据因素之间发展趋势的相似或相异程度，来衡量因素间关联程度的一种方法. 老化可以看做是环境这个复杂系统对材料作用而产生的一个过程机制不清晰的灰色系统，通过统计方法将多个自变量的序列和材料性能因变量序列的几何形状相似程度排序[22]，其基本思想是将评价指标原始观测数进行计算关联系数、关联度以及根据关联度的大小对待评指标进行排序. 灰色关联度分析过程如下：

首先确定反映系统行为特征的参考数列N（此处为PC失效性能）：

以及影响系统行为的比较数列N（此处为环境因素）：

然后进行关联系数的计算，过程如公式（8）所示.

其中，i为第i个环境因素，k为该因素中第k个样本值. min为向量最小值，max为向量最大值. 为分辨系数，考虑到兼顾老化行为数据序列的差异显著性与系统整体性，ρ这里取0.5.

由于信息过于分散不便于进行整体性比较，将关联系数求取平均值得到关联度数值，将得到的关联度数值作为比较数列与参考数列间关联程度的数值表示. 最后将关联度进行排序，关联度高低代表材料失效性能数列与环境因素数列的相似程度. 由此通过环境因素数据矩阵与材料老化变量间灰色相关性系数，挑选对材料老化影响较大的环境因素.

1.3.3 反向传播人工神经网络模型（BP-ANN）

将环境因子和老化程度值通过人工神经网络构建的拓扑结构进行学习训练，基于材料数据与环境数据获得的路径规律，建立两者的关联，实现对其他未知地区老化数据的预测. 其基本算法包括两个方面：信号的前向传播和误差的反向传播[16].环境数据提供给输入层后，神经元的激活值从输入层经各中间层向输出层传播，输出材料老化值，误差从输出层经过各中间层逐步修正各连接权值，最后回到输入层，随着这种误差逆的传播修正不断进行，网络通过输入层环境数据模拟输出层材料老化数据的正确率也不断上升[17].

2 分析与结果

2.1 西藏地区PC老化行为

通过跟踪测量PC在10个大气站点暴晒3、6、9、12个月期间的表观性能（如失光率、色差）和力学性能（如拉伸强度、拉伸断裂应变等）指标，表征PC在西藏典型地区的老化行为，如图2所示.

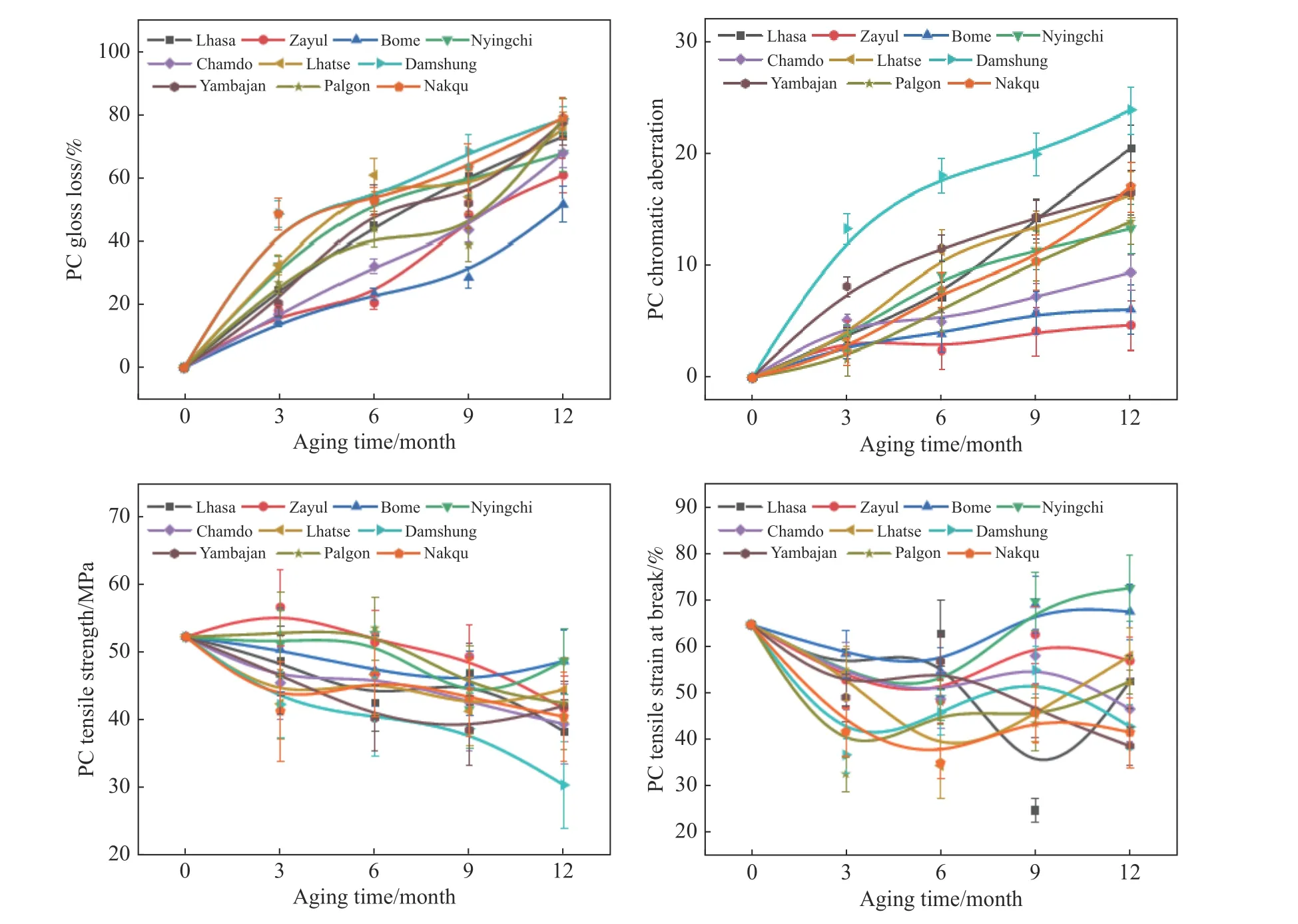
图2 PC老化性能随暴晒时间变化. (a)失光率; (b)色差; (c)拉伸强度; (d)拉伸断裂应变Fig.2 Aging performance of PC as a function of exposure time: (a) glossiness lost rate; (b) chromatic aberration; (c) tensile strength; (d) tensile strain at break

从图2中可以看出，相对于失光率、色差等表观性能，力学性能（如拉伸强度、拉伸断裂应变）数据波动性较大，规律性较差. 但是可以看出，PC拉伸强度在试验过程中，整体呈下降趋势，其中当雄、羊八井等地下降幅度较大，而察隅、林芝在试验9个月过程中下降幅度较小. PC失光率、色差在试验过程中整体趋势不断增加，两者规律比较接近，其中色差数据规律性最好. 在老化过程中，察隅、波密、林芝及昌都等低海拔地区的样品色差出现了逐步上升趋势，班戈、那曲等藏北地区的色差出现先下降再上升的变化规律，但色差值并不高，老化程度稍轻. 而在当雄、羊八井等高海拔地区及拉孜等藏南地区色差大，老化程度严重.

评价西藏地区各个区域大气环境严酷度，需要选择能反映材料老化损伤程度、数据具有规律性、各站点数据具有差异区分度的指标. 由于自然暴露试验时间较短，力学性能数据离散性较大，选用规律性较好的表观性能数据能更清楚反映PC的老化行为；参考GB/T 4796—2017[33]《环境条件分类 环境参数及其严酷程度》，PC色差值是行业认可的高分子老化严酷度评价指标. 综合以上分析，从上述4个指标在4个周期的数据中，选择PC自然暴露试验12个月的色差值作为大气环境严酷度评价指标.

2.2 PC表观损伤敏感环境因子

西藏大气环境对PC作用机制目前没有明晰的数学模型，西藏环境数据也可以看做是一个信息模糊、变量多维的集合. 通过皮尔逊相关性分析、灰色关联分析、回归分析等数学方法，定量分析西藏环境因素（包括地理因素如海拔高度、经度、纬度等，及气候因素如年平均相对湿度、年平均温度、降水时间、日照时间、风速、平均气压、累积降水量等）和高分子材料表观性能（PC色差）之间的相关性，寻找影响PC材料表观老化的敏感环境因子.

2.2.1 Pearson相关性分析环境因子间关联

各环境因素并非独立变量，通过Pearson分析西藏地区环境因素间相互影响程度，为筛选敏感环境因素提供数据支撑. 环境因素间Pearson相关性系数分析结果如图3（a）所示. 相关性高低通过Pearson系数的绝对值表示，绝对值大代表相关度高（用橙色表示），绝对值小代表相关度低（用蓝色表示）. 正相关则表示两环境因素间存在一定促进作用，负相关则表示两环境因素间存在一定抑制作用. 结果显示，降水时间、累积降水量、平均相对湿度、湿度大于80%时间等与水相关的参量间相关系数较高属于同类型参量（降水时间与平均相对湿度的Pearson相关性系数为0.899，累积降水量与湿度大于80%时间的Pearson相关性系数为0.84）；日照时间与降水时间、平均相对湿度等与水相关的参量高度负相关（日照时间与降水时间的Pearson相关性系数为-0.81，与平均相对湿度的Pearson相关性系数为-0.86），而海拔高度几乎与重要环境参量相关性都较高，是影响降水、日照、湿度等变化的本质原因（海拔高度与平均相对湿度负相关，Pearson相关性系数为-0.611，与日照时间的Pearson相关性系数为0.711）. 在挑选敏感环境因子过程中，尽量挑选高度负相关的因子，可全面反映PC老化环境因素；对于高度正相关的因子，由于其表达信息相关性较高，可在多个参量中选择一种合适的作为敏感环境因子.

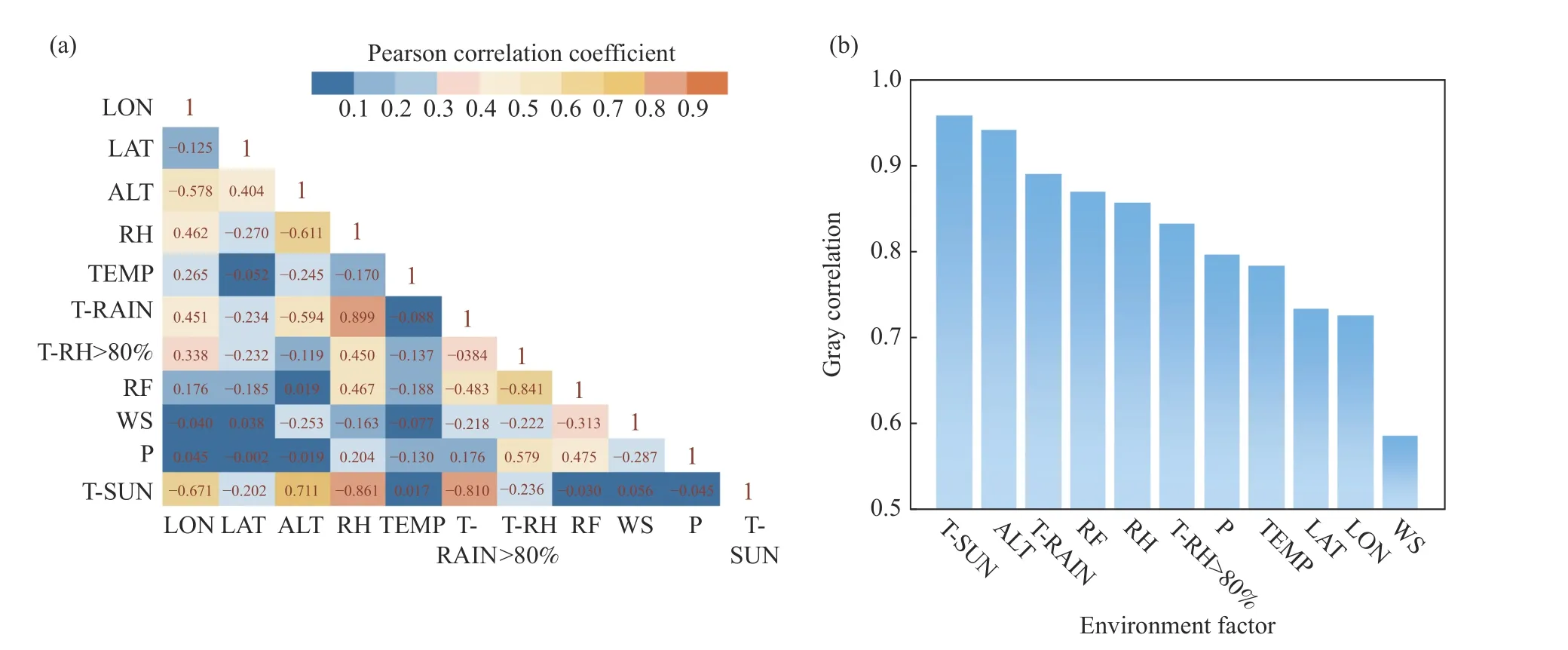
图3 西藏环境因素关联分析. (a)环境因素间Pearson相关性系数; (b)环境因素与PC色差灰色关联度Fig.3 Correlation analysis of the environmental factors: (a) Pearsonʼs correlation coefficients between the environmental factors; (b) grey relationships between the environmental factors and PC chromatic aberration in Tibet

2.2.2 灰色关联度分析PC老化敏感环境因子

本项目以PC材料色差作为环境效应数据母系列，以环境因素作为子系列进行灰色关联分析，通过MATLAB软件编程计算PC色差与环境变量间的灰色关联度，作为衡量影响PC色差变化的参量. 灰色关联度结果按照从大到小排序，依次为日照时间、海拔高度、降水时间、累积降水量、年平均相对湿度、湿度大于80%时间、平均气压、平均气温、纬度、经度、风速（图3（b））.

2.2.3 基于线性回归分析的PC色差敏感环境因子

线性回归分析可用于定量计算两个变量间线性相关程度，是判断两个变量能否建立线性函数的前提. 选择在灰色相关性分析中得出的对PC色差影响最大的前8个环境因素，通过散点图探究其与PC色差值间线性关联程度，建立线性回归方程，如图4所示.

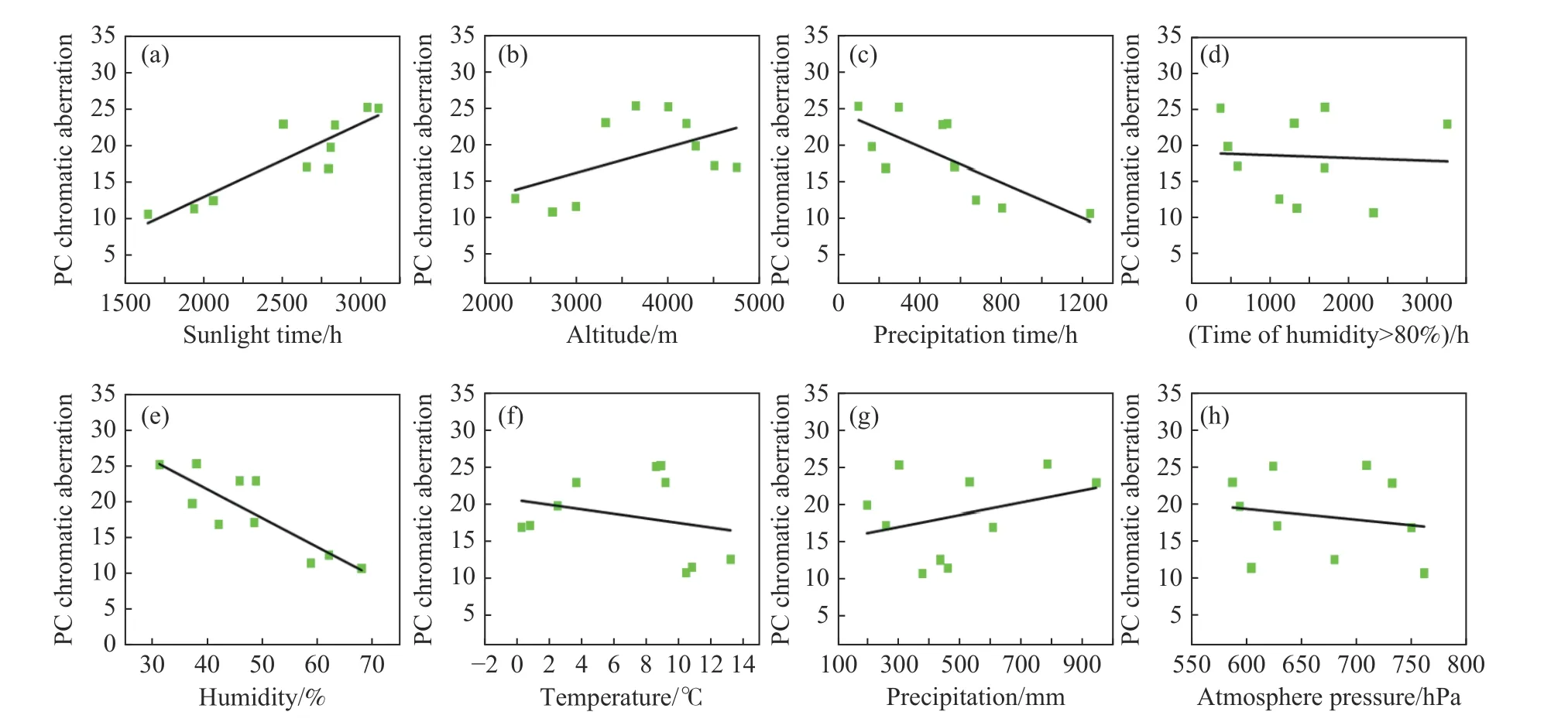
图4 各环境因素与PC色差线性回归图. (a)日照时间；(b)海拔高度；(c)降水时间；(d)湿度大于80%时间；(e)平均相对湿度；(f)平均气温；(g)累积降水量；(h)平均气压Fig.4 Linear regression plots between the PC chromatic aberrations and environmental factors: (a) sunlight time; (b) altitude; (c) precipitation time; (d) time of humidity>80%; (e) mean relative humidity; (f) mean value atmospheric temperature; (g) cumulative precipitation; (h) mean atmospheric pressure value

计算各环境因素与色差值间的回归方程，通过对比拟合优度（R2）、Pearson相关系数，量化比较各环境因子与PC色差间关联程度大小，结果如表2所示.

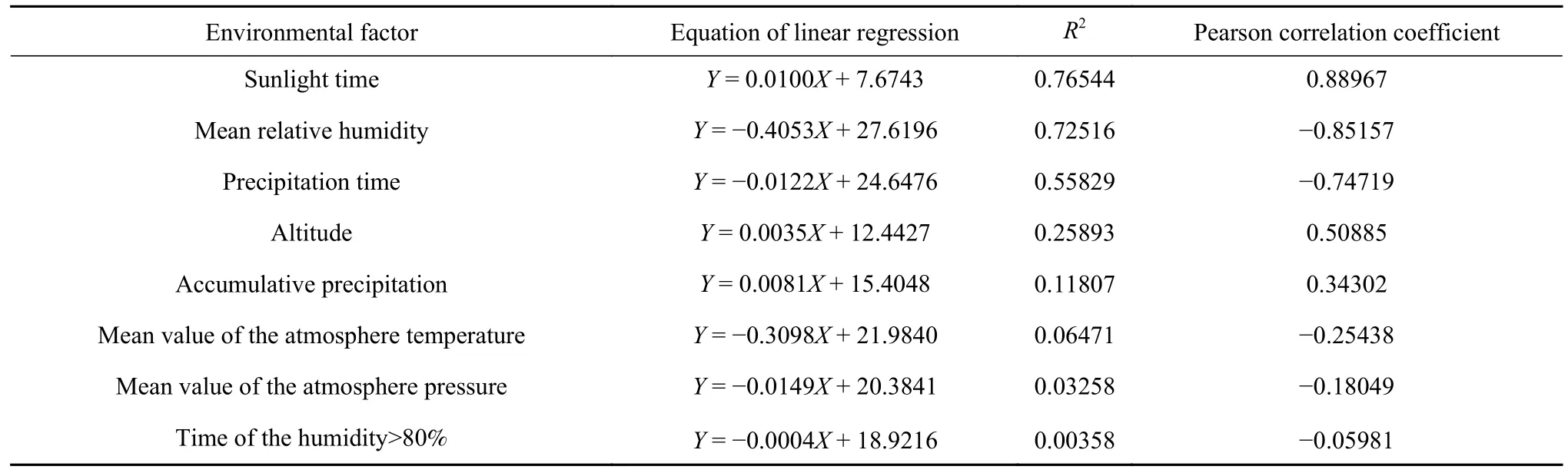
表2 西藏地区各环境因素与PC色差线性回归分析结果Table 2 Results of the linear regression analysis between the PC chromatic aberrations and environmental factors

由表2可知，各线性回归方程的拟合优度最高为0.76，低于0.85阈值，表明各环境因素与PC色差间并没有统计意义上的严谨线性关联[20]，说明线性方程并不能很好地建立环境因素与PC色差性能间映射关系. 我们对拟合优度R2大小进行排序，比较各因素与PC色差间相关性大小，以此筛选影响PC老化的敏感环境因素. 结果可知，敏感显著的环境因素依次为日照时间、平均相对湿度、降水时间、海拔高度.

Pearson系数表明两个变量间在统计学意义上的相关性[20]，而从表2中可知，仅日照时间与PC色差之间有较好的相关性，Pearson系数达到0.889.平均相对湿度、降水时间与PC色差相关性虽然较高达到-0.85、-0.747，但是为负相关. 基于PC材料老化失效机理，并非为湿度、降雨抑制了PC老化，而是因为在西藏地区，湿度、降水较大的样本地区海拔低，日照强度低；而相比于湿度与降雨，日照是影响PC老化的主要因素[2,4]，低日照强度使得PC色差并不如高海拔地区，所以湿度、降雨与PC老化呈负相关.

基于PC老化行为与机制分析，并综合考虑上述Pearson相关性、灰色关联分析、线性回归等各方法计算得到的相关性较高的环境因素，优先选择日照时间、海拔高度、平均相对湿度、降水时间作为PC表观色差老化敏感环境因素较为合理.

2.3 基于人工神经网络的PC色差预测模型

PC的老化是光照、温度、水分多种因子耦合作用的复杂过程，BP人工神经网络能够建立“环境-材料”间复杂的非线性映射关系. 这里以上述章节讨论得到的敏感环境因素（日照时间、海拔高度、平均相对湿度、降水时间）为输入变量，以PC色差值作为输出变量，以10个站点环境与材料数据为建模样本，采用循环留一法（即将10个样本分为9个训练样本1个验证样本，轮换验证样本，一共训练10次）验证模型的泛化能力，结果如图5（a）所示，10次训练过程最大误差不超过0.9.

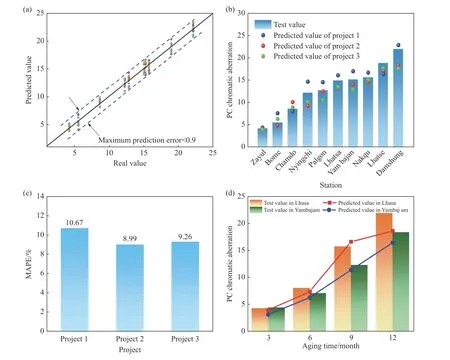
图5 PC色差预测BP-ANN模型优化. (a)循环留一法训练过程；(b)三种方案训练预测结果；(c) 三种方案训练误差；(d)模型对新地点PC色差老化预测精度Fig.5 Optimization of the BP-ANN model for the prediction of PC chromatic aberration: (a) training results of the rotational-one-leave method;(b) predicted results of the three models; (c) mean errors of the training results for the three models; (d) precondition accuracy of the PC chromatic aberrations in the new locations

BP人工神经网络模型中重要参数设置如下：输入层激活函数选为tansig，输入层到隐含层使用tansig函数，隐含层到输出层使用purelin线性函数，训练函数选择为自适应强的traingdx函数[16].另外，为了获得最优模型，研究学习精度这一重要模型参量对预测能力的影响. 如图5（b）所示，方案一、二、三分别为学习精度设置为0.1、0.01、0.001的模型. 结果如图5（c）所示，发现方案二的模型MAPE（平均绝对百分比误差）值最小（8.99%）. 这是因为方案一中过低的学习精度可能会引起模型网络构建不足，拟合不充分，预测误差较大；而方案三中过高的学习精度可能会导致过拟合，反而降低模型泛化能力，也将导致预测误差大[20,23]. 基于以上研究，最终可构建具有高精度预测能力的PC色差值预测模型.

基于该BP-ANN模型，预测本研究课题组试验地：拉萨、羊八井站点，PC自然环境暴露1 a（2019年3月—2020年2月）色差值. 通过输入试验段时间的年均值，得到PC在两站点老化3、6、9、12个月过程色差预测值. 该结果与实际测量值对比，如图5(d)所示，发现其误差小于7.6%，因此，基于优化后的BP-ANN模型对西藏地区PC老化色差值具有良好的预测能力.

基于上述BP-ANN映射模型，通过输入西藏28个城市敏感环境因素数据，预测得到PC在西藏28个城市的老化色差值，如图6（a）所示. 构建关联性最高的两个敏感环境因素——日照时间、海拔高度与PC色差预测值散点图，通过曲面拟合，呈现人工神经网络模型函数映射关系，如图6（b）所示. 图中颜色由蓝色过渡到红色，代表严酷程度由小到大. 从模型三维图像中可以看出，在海拔较高、日照时间较长的地区的严酷度明显高于海拔较低、日照时间短的地区的严酷度. 通过该环境-色差映射三维图像，可以构建环境与严酷度的对应关系.

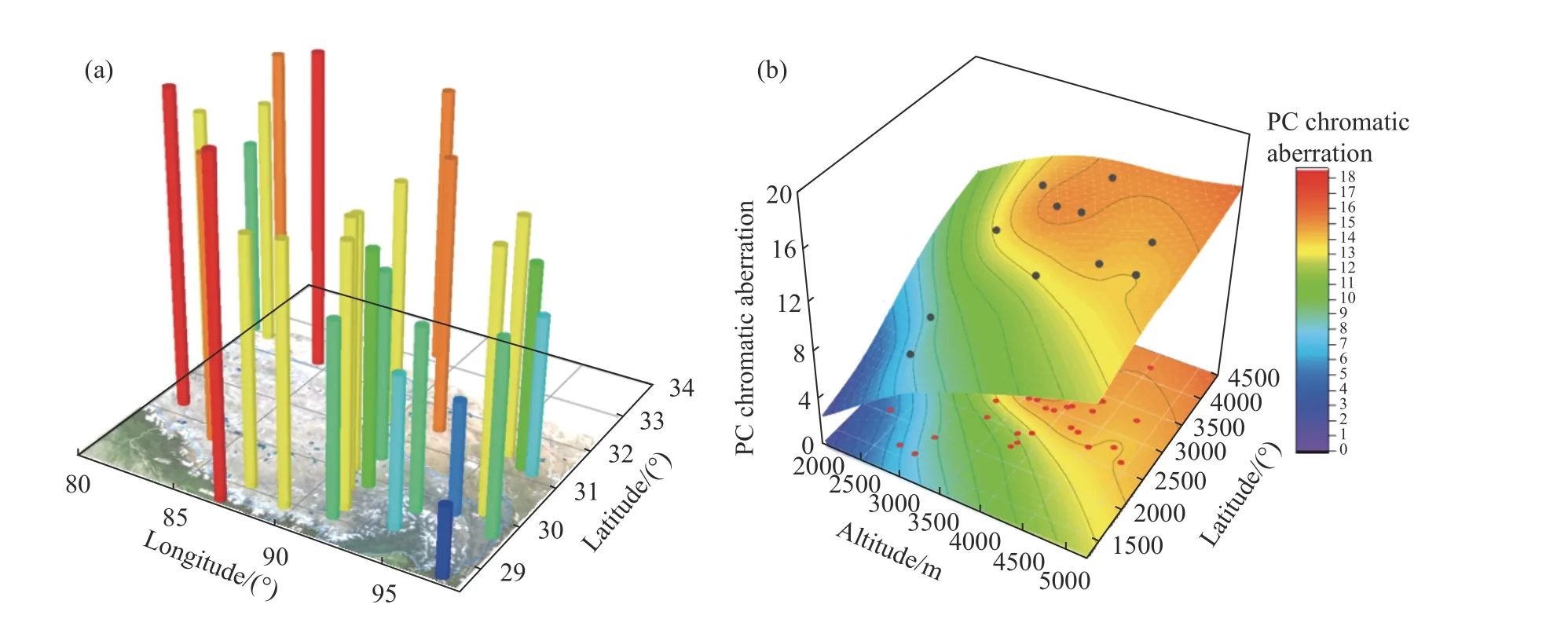
图6 (a)西藏地区PC色差预测值；(b)西藏地区敏感环境-PC色差映射关系图Fig.6 (a) Predicted value of the PC chromatic aberration in Tibet; (b) mapping plot for the relationship between sensitive environmental factors and PC chromatic aberrations in Tibet

2.4 基于PC色差值的分布地图绘制

基于BP-ANN建立PC老化3、6、9、12个月色差值与敏感环境因素间的映射模型，输入西藏28个城市站点的敏感环境因素数据，预测得到PC在西藏28个城市老化3、6、9、12个月的色差值. 通过Matlab软件，对28个站点以外的西藏全域进行Griddata插值计算，得到PC在西藏地区不同老化时间色差值分布地图，如图7（a～d）所示.

图7 西藏地区PC老化色差分布地图. (a)老化3个月；(b)老化6个月；(c)老化9个月；(d)老化12个月Fig.7 Chromatic aberration distribution plots of PC aged in Tibet: (a) aged for 3 months; (b) aged for 6 months; (c) aged for 9 months; (d) aged for 12 months

从图7可见，在老化3个月之内，西藏全域色差值分布并没有明显差异，表明此时PC尚未发生明显老化，无法区分各地区严酷度. 6个月后，藏东地区老化依然较轻，而其他部分尤其是藏北开始发生较明显老化. 9个月之后，色差值在藏东南较低，而在藏西北高. 到12个月时，藏西阿里无人区及藏北高原PC老化色差值显著增加，藏南与藏中次之，而藏东色差值依然较低，且范围越来越小.

以上分布表明，西藏地区海拔较高的藏北及藏西阿里无人区，太阳辐照强度高、日照时间长，对PC老化作用强，大气环境严酷度高；而海拔较低的藏东，虽然平均温度较高，但是日照强度低、对PC老化作用稍弱，大气环境严酷度低.

2.5 西藏大气环境严酷度预示

环境因素不仅在西藏各地区分布有差异，在时间尺度也有差异. 典型敏感环境因素时空分布特点如图8（a～d）所示. 西藏每年10月至翌年4月为干季，降水稀少；5～9月为雨季，降水充沛. 西藏夏季气温并不高，藏北高寒地带常年低温. 全年湿度较低，其中7～9月份平均湿度高值达60%～70%，而其余时间低至40%～50%，最低在1月湿度甚至低至25%～30%.

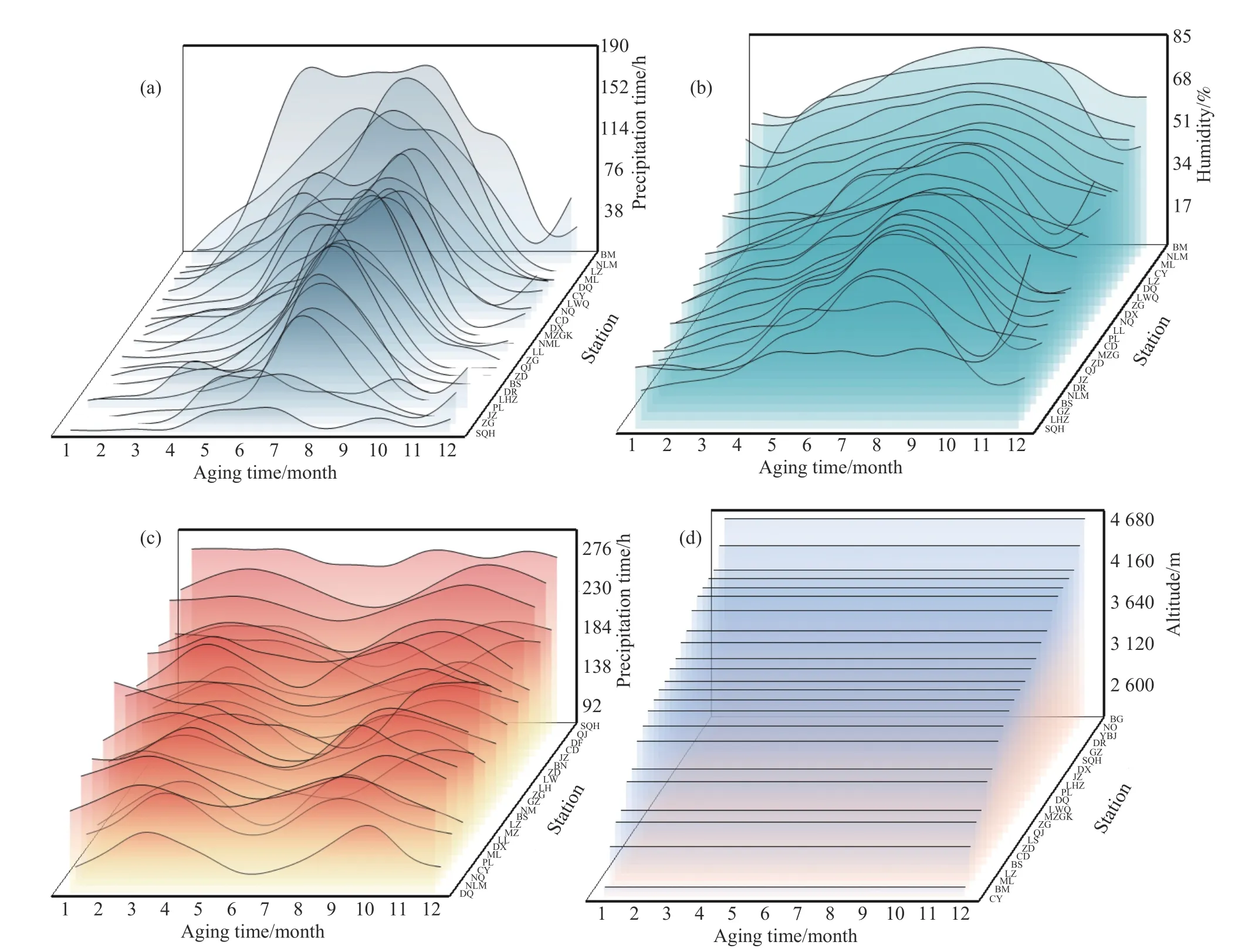
图8 西藏环境因素月均值变化与年均值Fig.8 Monthly and annual mean values of the environmental factors in Tibet

基于上述研究构建的“敏感环境年均值-PC色差”映射模型，通过向该模型输入西藏各城市敏感环境因素逐月均值，得到色差逐月值，如图9所示. 该色差逐月值并非表示PC材料在某月的具体老化色差数值，而仅作为一种大气环境严酷度评价指标，定量描述该月份大气环境严酷度. 基于Griddata插值计算，得到严酷度空间分布的逐月动态变化，结果如图9所示.

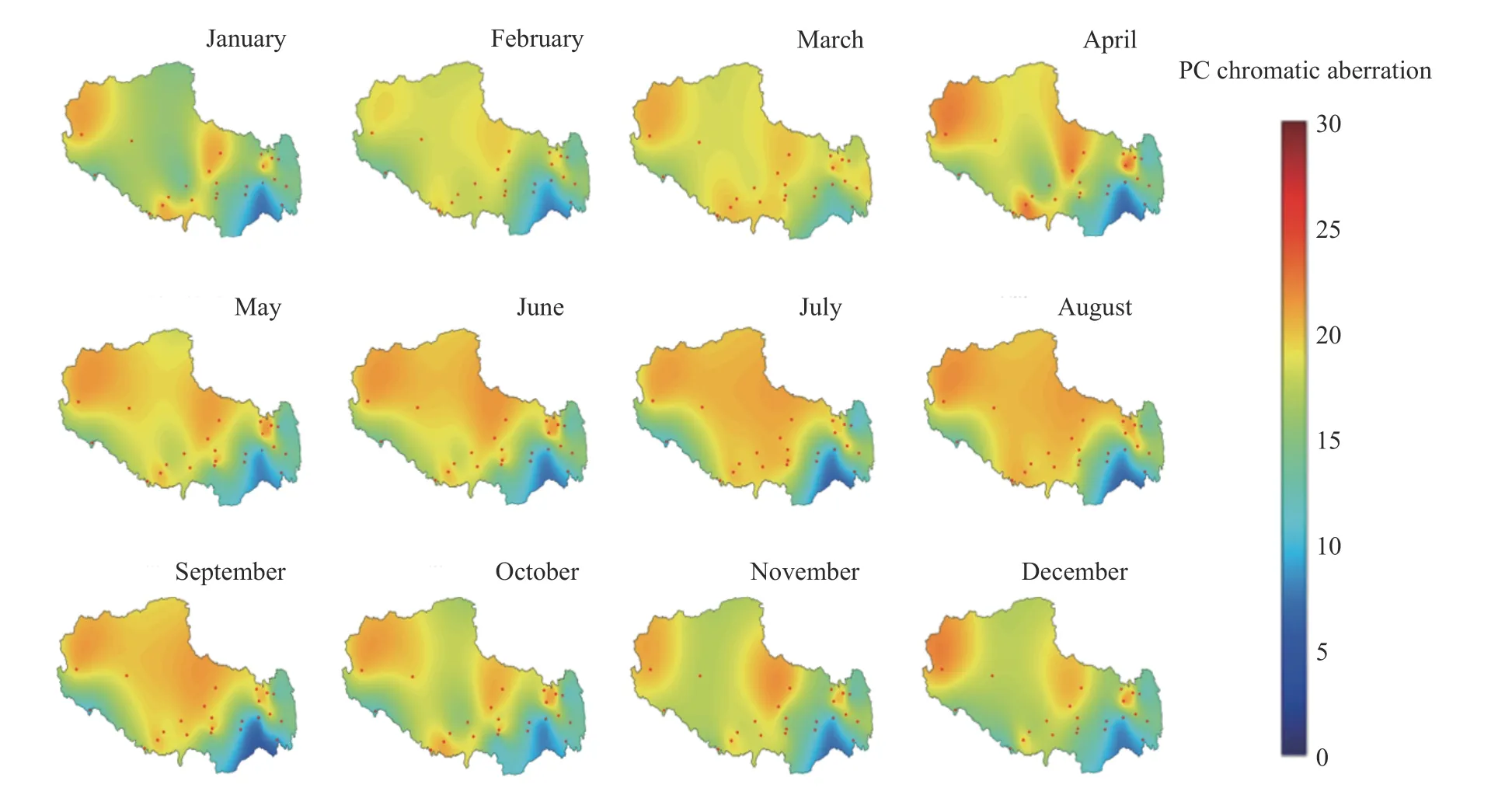
图9 基于PC色差值的西藏大气环境严酷度逐月图Fig.9 Atmospheric environmental severity map of Tibet for all months based on the PC chromatic aberration

由图9可知，西藏地区环境严酷度夏季高于春秋冬季. PC色差整体情况在6～9月份数值最高，红色区域几乎覆盖整个藏中及藏西北地区，表明在夏季PC严酷度最高. 藏东低海拔地区，在夏季PC老化程度也相比于冬季较高. 在10月至翌年2月，红色区域明显减少，这是因为冬季气温降低、日照强度减弱，西藏仅剩那曲等高海拔地区保持高严酷度.

3 结论

（1）通过对聚碳酸酯（PC）在西藏自治区（西藏）10个典型大气站点开展自然暴露试验3、6、9、12个月，采集其表观性能（失光率、色差）及力学性能（拉伸强度、拉伸断裂应变）等数据，基于老化行为分析，发现色差数据规律较强，反映了PC材料在西藏各地老化行为差异，选择以PC老化12个月色差值作为严酷度评价指标. 由Pearson相关性分析、灰色关联度分析、回归分析筛选出影响PC色差的4个敏感环境因子分别为日照时间、海拔高度、平均相对湿度、降水时间.

（2）PC老化是多种环境因子耦合作用的结果，通过训练10个站点敏感环境因子、色差样本数据，构建学习精度适中的、具有良好泛化能力的BP-ANN模型，建立“环境-材料”两者之间的映射关系. 通过输入西藏全域28个站点敏感环境因子，预测得到PC在西藏各地色差值，基于Griddate插值得到西藏地区大气环境严酷度分布地图，结果显示藏东等低海拔地区严酷度较低，而藏西无人区及藏北高原等高海拔地区严酷度较高.

（3）通过向模型输入各城市敏感环境月均值，预测得到基于PC色差值的西藏大气环境严酷度逐月图，作为大气环境严酷度预示预警，基于该地图可迅速划分大气环境严酷度时空分布规律，结果表明西藏夏季严酷度远远高于冬季，而冬季藏西北等地区严酷度依然保持较高值.