大功率磁悬浮泵宽流道叶轮的水力性能分析

白晓蓉, 胡 亮, 阮晓东, 苏 芮, 傅 新

(浙江大学 流体动力与机电系统国家重点实验室, 浙江 杭州 310027)

引言

自20世纪80年代初,BRAMM G等[1]提出了第一台磁悬浮泵实验模型,从此,磁悬浮泵在生命医学领域人工心脏血泵方面的应用有了较大的发展。随着半导体领域的发展,湿法制成用泵应用场合多变,不同工况的流量和压力差异很大,运行工况相比血泵要复杂得多。半导体制造等领域对化学品工艺介质有超洁净的输送需求。超洁净流控元件是光刻机、刻蚀机、离子和注入机等各类半导体制造装备机台中的核心基础件[2-3]。泵作为流控系统的动力元件,与输送介质密切接触。传统离心泵通常需要通过轴承与电机连接进行驱动与传动,存在动密封摩擦,同时存在泄漏风险。离心泵中摩擦产生的表面颗粒物脱落与泄漏均无法满足超洁净流控元件的需求。而磁悬浮泵是一种无轴承、无润滑、无密封且无机械部件摩擦的流体元件。

如图1所示,该泵将无轴承永磁薄片电机与泵体结构一体化,其永磁体转子被包覆在叶轮内部,工作时由电机驱动绕组和悬浮绕组产生的磁场来主动控制永磁体转子的3个自由度,其他3个自由度则依靠磁阻力实现被动悬浮。该泵的叶轮和泵壳由耐化学腐蚀的高纯度氟树脂(PFA或PTFE)制成,且叶轮转动过程中无摩擦,大大减少了流体输送过程中污染颗粒产生的风险,与隔膜或波纹管等泵相比,磁悬浮泵具有结构简单、运行可靠、易维护等优点,在浸没式光刻、单晶圆清洗、涂胶显影、CMP等半导体设备中被认为是最佳的流体输送元件[4]。

图1 磁悬浮泵结构示意图

由于磁悬浮泵具有无轴承、无润滑、无动密封、零泄漏等突出优点,已广泛应用于半导体湿法制程,同时在制药、食品、化工及军工等应用领域也有极大的应用需求,但某些应用场合往往需要更大的工作流量和压力,即大功率的磁悬浮泵。目前,瑞士Levitronix公司是中大流量磁悬浮泵的全球唯一供应商。

大功率磁悬浮泵由于其特有的水力结构,其泵送效率较低,此外其仅能依靠磁场悬浮刚度与平衡孔抵消轴向液压冲击力,当电机功率较小时,轴向被动磁阻力基本可以平衡叶轮的液压轴向力。然而随着功率的增加,磁悬浮泵的液压轴向力平衡问题越发突出,此时叶轮将不能够正常工作甚至触碰泵壳造成破损或摩擦污染。

目前,国内外对有关磁悬浮泵高效水力特性研究的公开文献报导较少。RAGGL K等[5]在综合考虑水力因素、电驱动系统和电力电子技术下,对整个泵送系统进行了综合优化,目标是实现最大输出压力、最小容积的泵系统。陈超[6]设计了无轴承薄片离心泵系统,最大流量达到9 L/min,但效率不高。

对于磁悬浮泵的液压力平衡问题,国外研究学者已对其进行了一定的研究,RAGGL K等[5]研究了液压轴向力随叶轮半径比例增大的倍数规律,表明轴向液压力增加速度为轴向磁阻力的2倍;BOESCH P N[7]认为更高性能的磁悬浮离心泵叶轮的轴向平衡是必须解决的最困难任务之一,为此提出了平衡孔+阻塞板、平衡孔+顶阀+阀环、平衡孔+凹槽等不同的轴向平衡方法,同时对不同类型的泵壳产生的径向力进行研究,认为环形泵壳体适用于小的工作流量,螺旋泵壳体适用于在最佳工作点处产生较大的流量。国内学者对传统离心泵液压轴向力及径向力研究较多,汪东山等[8]运用仿真研究了平衡孔位置对离心泵轴向力的影响;刘在伦等[9]通过试验研究了叶轮背叶片对离心泵轴向力的影响;陈帅[10]探究了双吸离心泵蜗壳断面面积规律、叶片布置方式以及叶片包角对离心泵叶轮部件所受径向力的影响。但目前国内针对磁悬浮离心泵的液压轴向力及径向力研究基本处于空白。

为此,本研究为探究高效率大功率磁悬浮泵的水力结构,基于Cfturbo软件设计了一种大功率磁悬浮泵的宽流道、螺旋形蜗壳的水力结构,同时为实现对照也搭建了窄流道、环形蜗壳的水力结构,并通过流体仿真对其进行水力效率、液压轴向力及径向力分析及对比,为高效率大功率磁悬浮泵的开发提供一定的技术支撑。

1 计算模型及计算方法

1.1 磁悬浮泵泵头几何模型

由于磁悬浮泵将磁悬浮电机与泵体结构一体化,所以磁悬浮泵头的设计需与前期设计的磁悬浮电机尺寸相配合。本研究首先基于CFturbo软件设计了磁悬浮泵叶轮及对应的螺旋形蜗壳,其次在此基础上将永磁体转子包覆在叶轮内部,同时为了平衡液压轴向力,设置了平衡孔、挡流板、背叶片等平衡装置。基本设计参数为：流量Q=200 L/min,压差Δp=0.24 MPa,转速n=5000 r/min,比转速nq=26。叶片采用圆柱形叶片,主要几何参数为：叶轮进口直径D1=33.6 mm,叶轮出口直径D2=83 mm,叶轮出口宽度b2=12.6 mm,叶片数Z=6,叶片进口安放角β1=28°,叶片出口安放角β2=35°,蜗壳基圆直径D3=91 mm。宽流道磁悬浮泵头叶轮几何模型及整体计算流体域如图2所示。

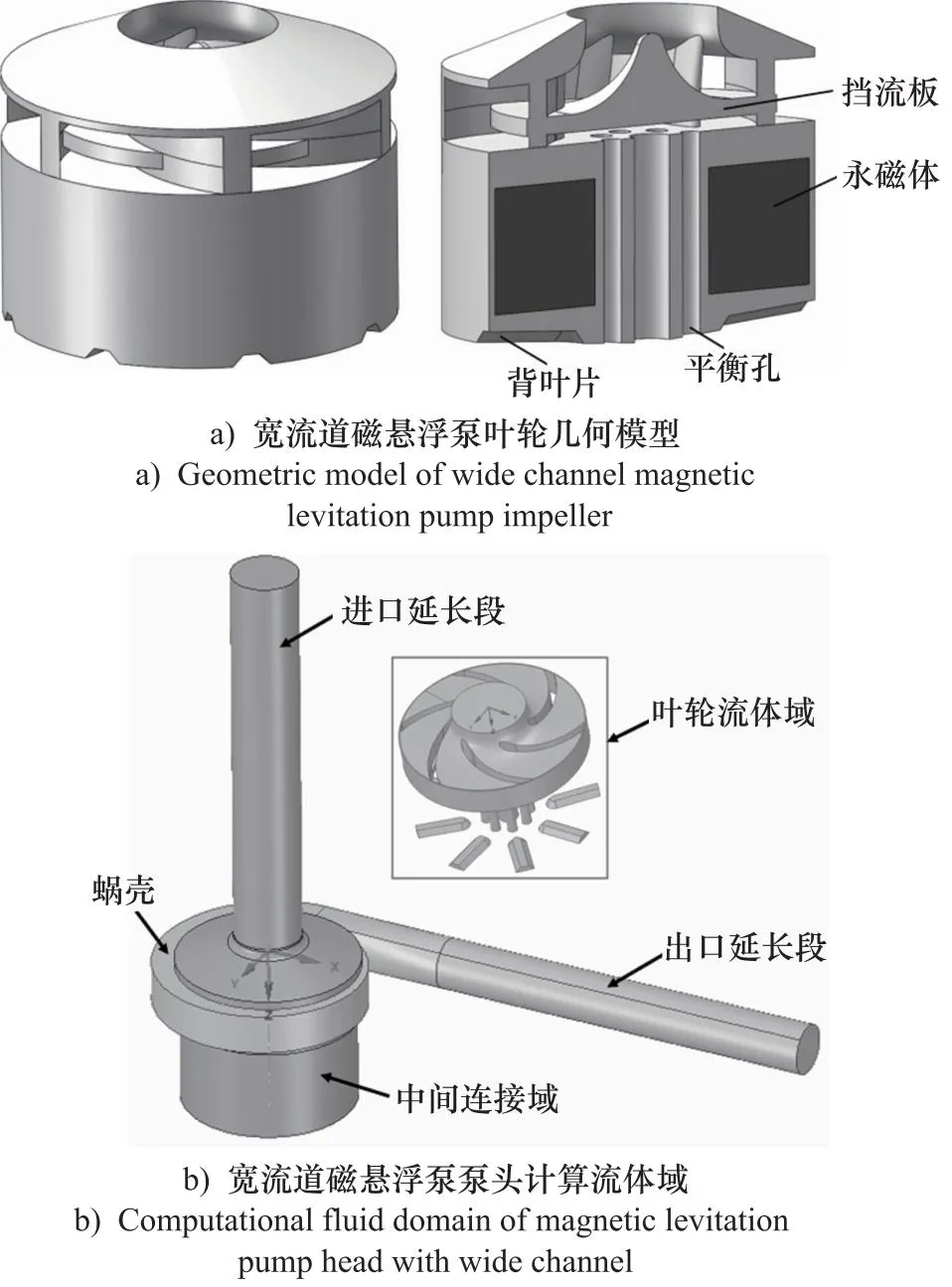
图2 宽流道磁悬浮泵泵头三维模型

为了实现对照,本研究也建立了窄流道磁悬浮泵模型,并对窄流道磁悬浮泵进行流场分析,磁悬浮泵窄流道叶轮三维模型及流体域,如图3所示。

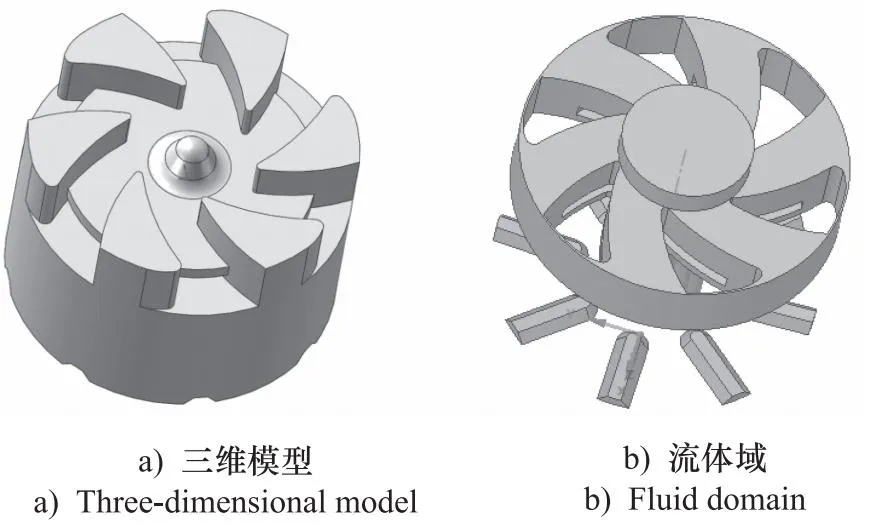
图3 窄流道磁悬浮泵叶轮模型

1.2 网格划分及无关性验证

在完成磁悬浮泵泵头三维模型的基础上,基于前处理软件Fluent Meshing软件对计算域模型进行网格划分。由于模型较为复杂,采用非结构化网格,并对叶轮、中间连接域较薄区域,蜗壳隔舌部分进行局部网格加密。同时为消除网格因素对数值模拟计算结果的影响,对模型的进出口总压差进行网格无关性检验。网格无关性结果如表1所示。

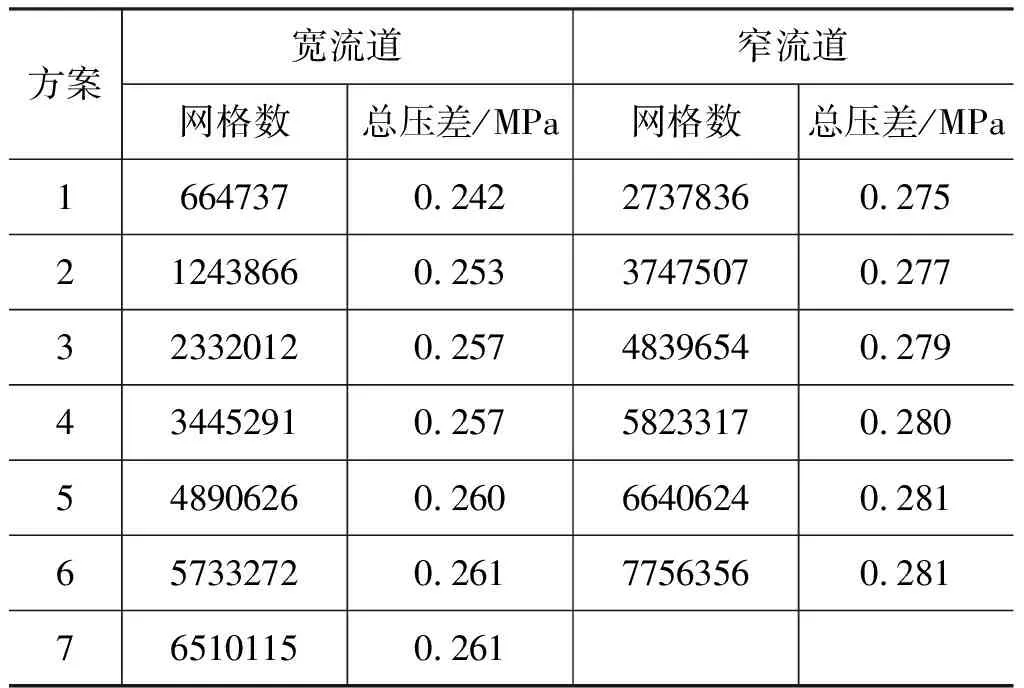
表1 宽窄流道磁悬浮泵计算域不同网格数方案Tab.1 Schemes of different grid numbers in the calculation domain of wide and narrow channel magnetic levitation pump

由表1可知,随着网格数的增加,总压差逐渐增大并趋于稳定。为保证网格计算精度,同时考虑节约计算时间,最终选取宽流道磁悬浮泵计算域网格数量为573.32万,窄流道磁悬浮泵计算域网格数量为664.06万。本研究宽窄流道磁悬泵将以上述所选网格模型作为后续研究。宽流道磁悬浮泵局部网格划分,如图4所示。

图4 宽流道磁悬浮泵网格划分局部图

1.3 计算方法与边界条件

数值模拟过程基于ANSYS CFX2020R2软件,湍流模型采用标准k-ε模型,对所有变量整场联立求解,同时求解连续方程和动量方程组。对流项选择为迎风格式,湍流数值格式采用一阶格式。边界条件设置为总压进口, 质量流量出口。在定常计算中,动静交界面设置为冻结转子模型,计算精度为10e-6;在非定常计算中,将定常计算的结果作为初始条件,动静交界面设置为瞬态转子-定子模型。在5000 r/min工况下,叶轮旋转周期为0.012 s,非定常时间步长设定为叶轮旋转3°,即时间步长为1e-4 s。

2 性能预测方法及泵头受力分析

2.1 外特性分析

在不同工况下完成泵的流场数值模拟后,可以得到磁悬浮泵进出口压差、转矩等数据,进而对外特性进行预测。

压差的计算：

Δp=pout-pin

(1)

式中,pin,pout为泵进、出口总压,Pa。

泵效率计算：

(2)

式中,Pe为泵的输出功率,P1为泵的输入功率;Q为体积流量,m3/h;M为液体对泵产生的等效轴扭矩,N·m;ω为叶轮旋转角速度,rad/s。

2.2 液压轴向力分析

由于磁悬浮泵叶轮转子内部装有永磁体,该永磁体为电机的转子,电机转子与定子之间通过产生磁场来驱动叶轮旋转,所以磁悬浮泵叶轮转子在运转过程中受到一个电机定转子之间形成的轴向被动磁阻力Fz,方向与叶轮轴向运动方向相反,如图5所示。同时叶轮转子也会受到轴向液压力, 如图6所示。由于叶轮本身上表面入口处与叶轮底部结构的上下不对称性,高压液体作用在叶轮上表面的轴向力为F1,其大小与半径r1,r2有关,方向向下;作用在叶轮下表面的轴向力为F2,其大小与泵腔壳下部的半径r2有关,方向向上。同时待输送的液体从入口到出口液流方向发生改变,液流由轴向偏转到径向会对叶轮组件产生一个向下的动反力F3,所以叶轮受到的轴向液压合力为F1,F2,F3的矢量和Fh[7],即：

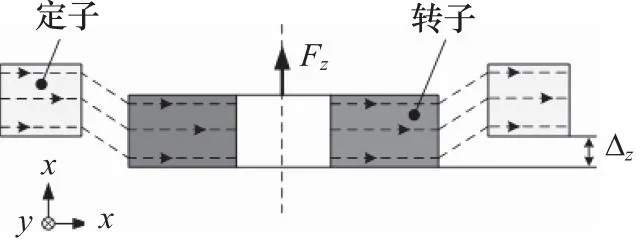
图5 叶轮转子受到的轴向被动磁阻力示意图

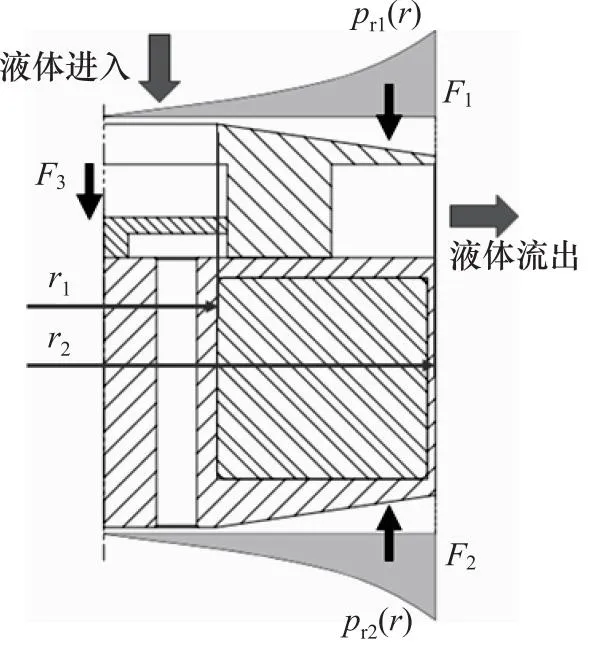
图6 叶轮受到的液压轴向力示意图

Fh=F2-F1-F3

(3)

(4)

F3≈ρ·Q·ΔVa

(5)

式中, ΔVa为叶轮进口和出口处绝对速度的轴向分量之差。

当轴向磁阻力Fz和液压轴向推力Fh相互抵消时,会产生稳定的轴向位置,即：

Fz+Fh=0

(6)

2.3 液压径向力分析

在径向上,磁悬浮泵叶轮转子在工作中会受到径向磁阻力和液压径向力的共同作用,该径向力主要由磁悬浮泵电机悬浮绕组产生的磁场通过负反馈来主动控制。如果液压径向力过大会对磁悬浮泵的主动悬浮控制造成相当大的压力,甚至使其无法工作,所以磁悬浮泵液压径向力的研究具有重要意义。

目前研究径向力的方法主要有3种,包括经验公式法、测试法以及数值模拟预测法[11]。本研究主要利用数值模拟来进行预测。叶轮液压径向力主要由液体作用于叶轮上的压力和黏性力所产生的,通过软件中的直接积分法可以得到叶轮X和Y方向上的径向分力Fx和Fy,再利用勾股定理计算出径向合力Fr。

3 仿真结果及分析

3.1 窄流道效应分析

下面以薄叶片-宽流道叶轮为对照,分析厚叶片-窄流道叶轮的窄流道效应,即分析叶轮的窄流道带来的水力损失影响。

首先,由于窄流道叶轮进口管道较细,来流速度大,如图7所示,在叶轮的中心入口处均形成了局部的高速液流团,高速液流团速度相对宽流道叶轮较高,液体直接冲击到叶轮的后盖板上,且后盖板中心导流弧度较小,同时由于窄流道叶轮叶片厚,部分流道被阻塞,通流面积小,使得冲击现象加剧,动能损失较大。相比较图7b,图7a中的宽流道叶轮后盖板中心导流弧度较大,同时在泵壳上部和底部速度分布较为均匀,能量损失较小。

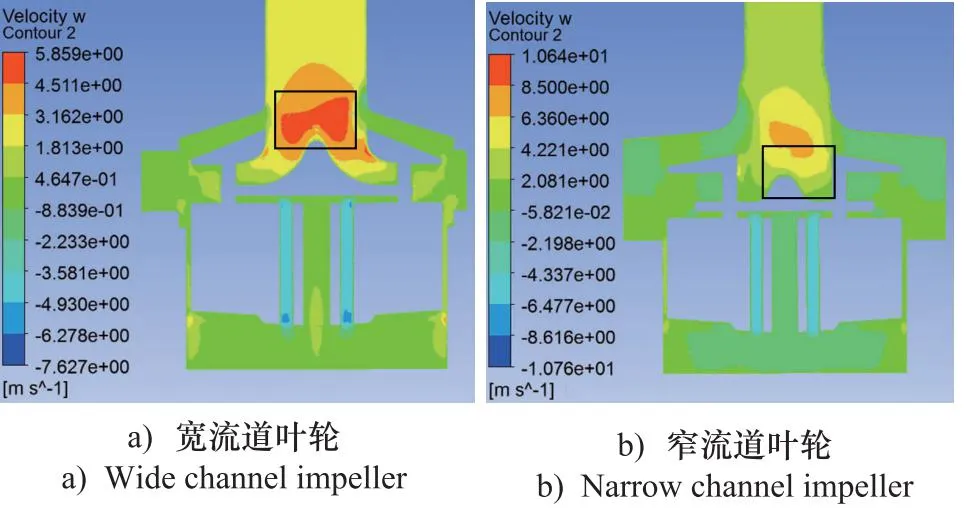
图7 磁悬浮泵泵头轴向截面速度云图

其次,由于磁悬浮泵本身的悬浮结构,使得叶轮转子与泵壳壁面之间存在着大面积的间隙,当叶轮悬浮在泵壳内高速旋转,转子与泵壳间在侧面和底面形成的间隙强剪切流动,产生了较大的摩擦损失。

同时,为了防止叶轮在启动关闭过程中由于轴向力的作用产生碰撞,叶轮上下表面与泵壳顶部和底部的间隙都较大,且叶轮出口压力较大,入口压力较小,使得叶轮上表面与泵壳顶部表面的间隙内的液体容易产生从出口向入口的泄漏回流,从而造成较大的容积损失。如图8b轴向截面速度矢量图所示,窄流道叶轮在顶部两边间隙内均产生了从出口到入口的泄漏回流。相比较图8b,图8a中在顶部间隙内仅在一边产生了从出口到入口的泄漏回流,这是由于顶部间隙另一边属于螺旋形蜗壳的螺旋起始段,如图9b压力云图所示,螺旋起始段流道较窄,压力作用在顶部间隙的面积较小,同时叶轮出口动能还未完全转换为压力能,未引起泄漏回流,所以宽流道叶轮的容积损失相对较小。

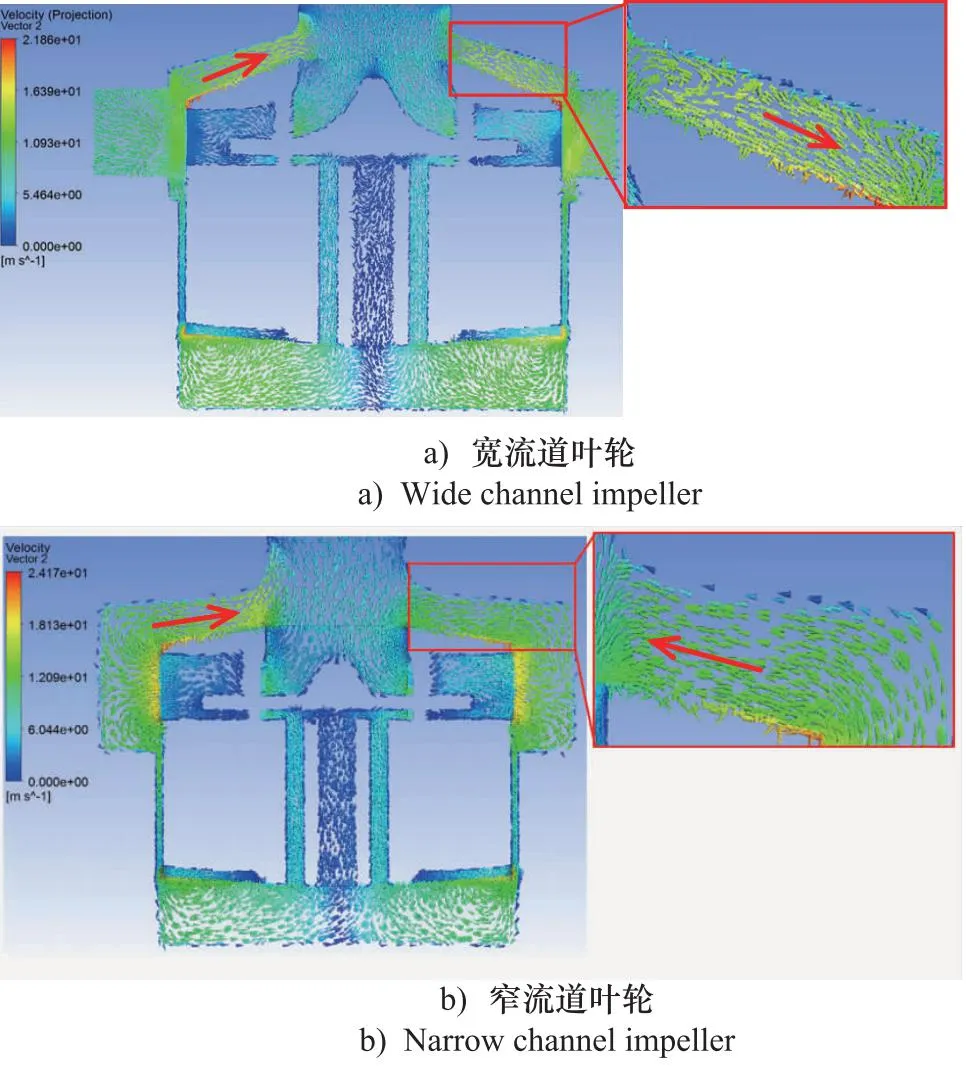
图8 磁悬浮泵泵头轴向截面速度矢量图

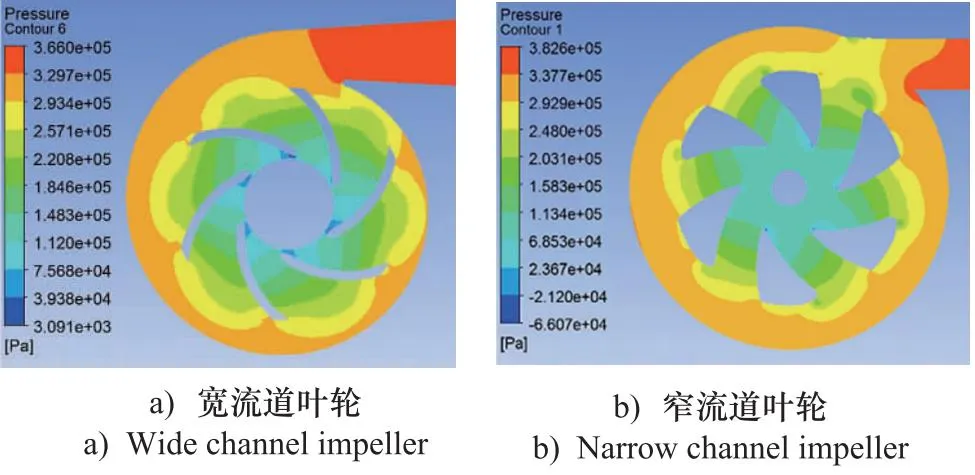
图9 磁悬浮泵泵头径向截面压力分布云图

最后在叶轮出口处具有尾迹轴向涡能量损失,如图10所示为磁悬浮泵泵头径向截面的轴向涡分布,轴向涡的正值代表旋涡方向与叶轮旋转方向相同,负值相反[12]。图10b中窄流道叶轮的出口与环形蜗壳的交接处整个弧度范围内均存在负的尾迹轴向涡分布,同时在中心处也有轴向涡的存在。而宽流道叶轮的出口与螺旋形蜗壳的交接处仅在靠近薄叶片两边存在尾迹,在交接处大部分弧度范围内均没有轴向涡的产生。所以与宽流道叶轮相比,窄流道叶轮的轴向旋涡能量损失较大。

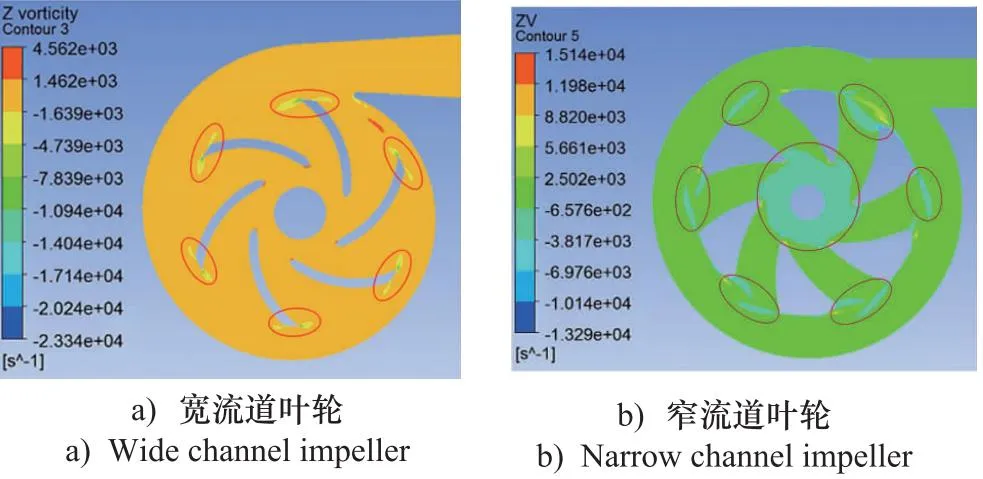
图10 磁悬浮泵泵头径向截面轴向涡分布

综上所述,窄流道叶轮的流体的入口冲击损失、摩擦损失、容积损失及轴向旋涡能量损失均较大,这些窄流道效应致使其水力效率较低。

3.2 宽窄流道磁悬浮泵的外特性对比分析

图11所示为叶轮转速5000 r/min工况下宽窄流道叶轮流量压差曲线对比图,从图中可以看出,宽流道叶轮和窄流道叶轮在流量小于125 L/min时,压差值随着流量的增加基本处于平稳状态,在流量大于125 L/min时,压差值随着流量的增加逐渐下降。当流量小于250 L/min时,宽流道叶轮的压差值略小于窄流道叶轮,当流量大于250 L/min时,宽流道叶轮的压差值大于窄流道叶轮,说明宽流道叶轮在大流量工况下的适用性更强。

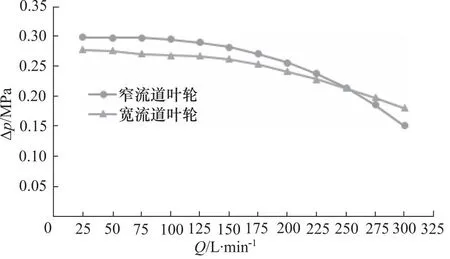
图11 宽窄流道叶轮流量压差曲线对比图

图12为叶轮转速5000 r/min工况下宽窄流道泵头效率曲线对比图,从图中可以明显看出,随着流量的增加,宽流道泵头水力效率最高可达59.4%,窄流道泵头水力效率最高为40.9%,且宽流道泵头水力效率随着流量的增加一直高于窄流道叶轮。当流量小于125 L/min时,宽流道泵头水力效率的提升量为1.6%～12.1%;当流量大于125 L/min时,宽流道泵头水力效率的提升量为14.0%～25.2%。由此可见,在流量-压差曲线基本一致的情况下,在大流量工况下采用宽流道泵头,效率提升更为明显。窄流道泵头由于窄流道效应致使其水力效率较低,从数值上验证了窄流道效应对磁悬浮泵水力效率的影响。

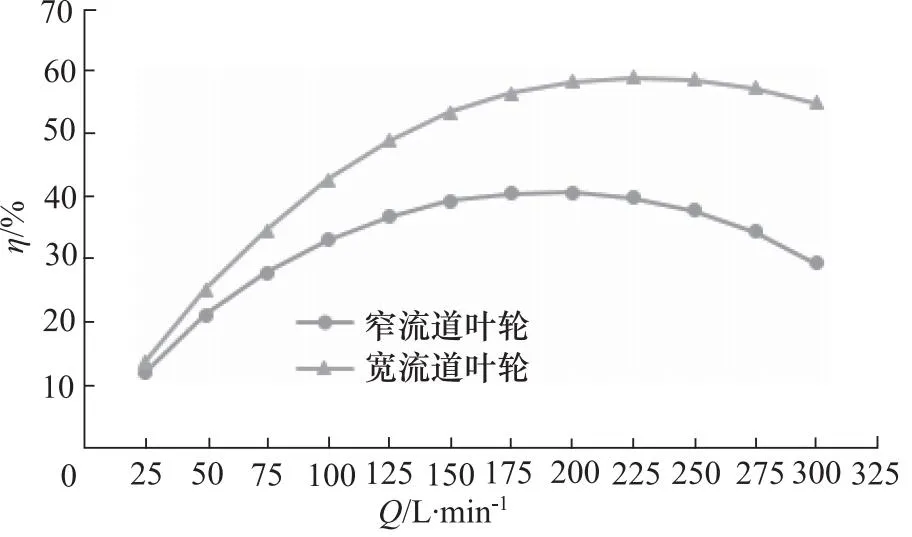
图12 宽窄流道叶轮效率曲线对比图

3.3 宽窄流道磁悬浮泵的轴向力对比分析

1) 叶轮转子被动轴向磁阻力仿真计算

磁悬浮泵叶轮转子轴向的平衡主要是磁悬浮泵电磁驱动部分产生的被动轴向磁阻力Fz和泵头部分液压轴向推力Fh之间的平衡。图13为叶轮转子相对于定子在轴向上移动不同位移时定子对转子产生的被动轴向磁阻力。本研究仿真模型中设定叶轮转子的轴向位移为dz=6.7 mm,根据图13中的拟合公式,得到叶轮转子在该位移时的被动轴向磁阻力为112.49 N。

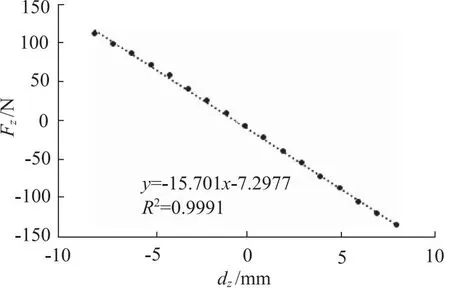
图13 叶轮转子被动轴向磁阻力仿真图

2) 叶轮液压轴向力仿真分析

图14为叶轮转速5000 r/min工况下,宽窄流道叶轮液压轴向力Fh随流量的变化曲线。可以看出,叶轮转子所受的液压轴向力随流量的增加而呈下降趋势,这是由于液压轴向合力主要与叶轮转子上顶面和下底面所受的压力有关,从图11流量-压差曲线可知,随着流量的增加,叶轮出口的压差值呈下降趋势,这与液压轴向合力的变化趋势相一致。从图14还可以看出,宽流道叶轮和窄流道叶轮所受的轴向液压合力基本一致,两者之间的差值较小,当流量小于75 L/min及大于250 L/min时,宽流道叶轮所受的轴向液压力略大于窄流道叶轮;当流量为75～250 L/min时,宽流道叶轮所受的轴向液压力略小于窄流道叶轮。

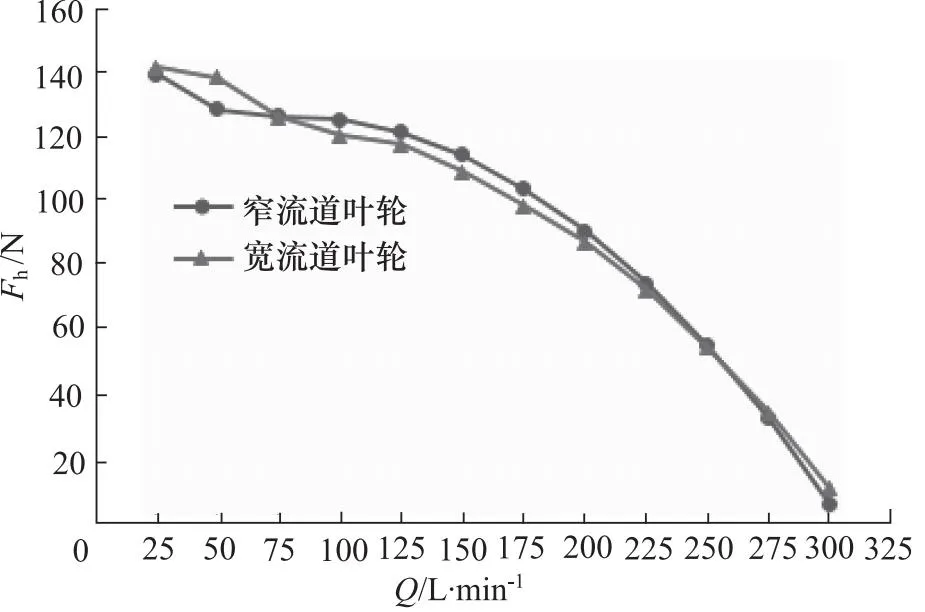
图14 叶轮转子液压轴向力仿真图

当叶轮转子轴向位置处于某个位置时,叶轮所受的液压轴向力并不是越小越好,需要与叶轮转子所受的被动轴向磁阻力相平衡使转子轴向稳定运转。图15所示为叶轮转子在达到平衡时所受轴向被动磁阻力与液压轴向力的差值转换成的可轴向移动的位移图。可以看出,在150 L/min时,叶轮转子可移动位移最小,宽流道叶轮转子和窄流道叶轮转子在dz为6.7 mm的基础上仅需移动-0.21 mm和0.12 mm即可达到平衡。在大流量工况下,转子所需移动的位移逐渐变大,最大可向下移动6 mm;在小流量工况下,转子所需移动的位移也逐渐变大,最大可向上移动1.8 mm。宽流道叶轮转子与窄流道叶轮转子可轴向移动距离相差不大。

图15 叶轮转子平衡可移动位移

3.4 宽窄流道磁悬浮泵的径向力对比分析

图16为叶轮转速5000 r/min工况下,宽窄流道叶轮一个周期内液压径向力的瞬态受力图,从图中可以看出,一个周期内叶轮转子的径向受力大小并不均匀。在径向上,磁悬浮泵叶轮转子上半部分叶轮叶片受到的液压径向力与下半部分包裹永磁体磁钢径向侧壁面受到的液压径向力方向不一定一致,叠加后呈现了径向力大小不均匀的分布。同时还可以看出,采用螺旋形蜗壳的宽流道叶轮的液压径向力要小于采用环形蜗壳的窄流道叶轮的液压径向力。

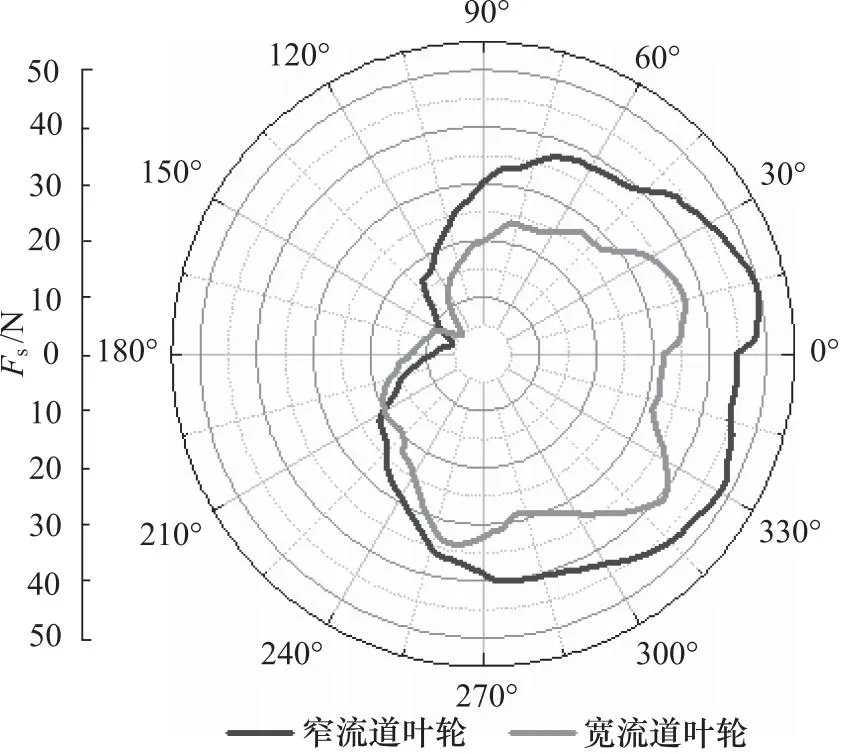
图16 叶轮转子液压径向力仿真图

4 结论

(1) 通过仿真阐述了窄流道叶轮流体的入口冲击损失、摩擦损失、容积损失及轴向旋涡能量损失等窄流道效应是磁悬浮泵泵头水力效率过低的主要原因;

(2) 本研究设计了一种大功率磁悬浮泵的宽流道叶轮,并对宽流道叶轮及窄流道叶轮进行水力效率对比分析。结果表明,在流量-压差曲线基本一致的情况下,在大流量工况下采用宽流道泵头,效率提升更为明显,提升量为14.0%～25.2%;

(3) 本研究对宽窄流道叶轮的液压轴向力及液压径向力进行对比分析,结果表明在流量-压差曲线基本一致的情况下,宽流道叶轮和窄流道叶轮所受的轴向液压合力基本一致,两者之间差值较小;采用螺旋形蜗壳的宽流道叶轮的液压径向力要小于采用环形蜗壳的窄流道叶轮的液压径向力。