空间耦合低密度奇偶校验码残差滑窗译码算法

周 华 李子杰

(南京信息工程大学电子与信息工程学院 南京 210044)

1 引言

低密度校验矩阵定义的卷积码由Jimenez等人[1]1999年首次提出。与分组码相比，低密度奇偶校验码(Low-Density Parity-Check, LDPC)卷积码在性能上卷积增益更大[2]。由于LDPC卷积码具有半无限空间交织校验矩阵结构，故其被命名为空间耦合低密度奇偶校验(Spatially-Coupled LDPC, SCLDPC)码[3]，其具有置信传播(Belief Propagation,BP)译码阈值接近对应规则LDPC码的最大后验概率(Maximum A Posterior, MAP)译码阈值的特性[4,5]。

SC-LDPC码研究主要包括编码码型的构造和译码方法的优化。针对SC-LDPC码型的构造，2016年，Koganei等人[6]提出一种空间耦合强度不均匀的编码方式，结果表明该码与具有均匀度分布的SC-LDPC码相比，具有更好的译码性能。2019年，Kwak等人[7]进一步提出了利用线性规划方法设计非均匀度分布的非规则SC-LDPC码，一定程度上提升了SC-LDPC码在二进制擦除信道下的译码性能。为了降低误码率和译码复杂度，Dehaghani等人[8]在2022年提出了一种基于小单链和循环结构相结合的码字集成方法。在译码研究方面，Iyengar等人[9]在2012年提出应用于SC-LDPC码的滑动窗口译码(Sliding Window Decoding, SWD)方法，与传统方案相比，较大幅度降低了译码复杂度与时延。2018年，Ali等人[10]针对滑窗译码提出了提前终止、消息重用(Message Reuse, MR)和有效信息放大3种方法，同时改善了滑窗译码的译码性能、复杂度和延时。同年，Zhu等人[11]针对滑窗译码中存在错误传播的现象，引入了同步机制算法。2020年，吴皓威等人[12]将分层译码引入窗口译码中，进一步降低SC-LDPC码的译码延时。张娅妹等人[13]也在当年提出了窗口扩展(Window Extension SWD, WE-SWD)滑窗译码方法，从而提高滑窗译码性能。

滑窗译码存在时延较高和译码性能较差的局限性，窗口内更新差异值较小的边信息对提高译码性能收益较低，且由于窗口内目标符号边信息更新受到前续窗口译码时关联边信息的影响，所以其更容易受到错误传播的干扰。为了提高SC-LDPC码滑窗译码性能和抑制错误传播，本文提出基于动态残差的滑窗译码(Residual SWD, RSWD)算法。该算法通过计算残差的方式动态选择窗口内更新前后边信息差异最大的边优先更新，降低边信息无效更新的频率，减少译码平均迭代次数，提高窗内译码收敛速度。仿真结果表明：相比于传统SWD算法，RSWD算法在窗口中各位置的误比特数明显降低，抑制错误传播现象更明显；在高信噪比区域或者低迭代次数的情况下，RSWD算法的误码率性能均优于SWD算法；将动态残差应用到消息复用和窗口扩展两种窗译码算法中，以牺牲较少复杂度为代价，提升窗译码性能。

2 空间耦合LDPC码

SC-LDPC码的构造基于原模图，原模图是由校验节点和变量节点组成的小型二分图，其与Tanner图结构类似。对单个原模图复制多次，然后通过边置换交织和扩展[14]的方式进行空间耦合可形成不同码长的SC-LDPC码[15]。规则LDPC码原模图的度分布为(J, K)，其中J表示原模图中连接到变量节点的边数，K表示原模图中连接到校验节点的边数。

图1展示SC-LDPC码原模图的构造过程，其中图1(a)所示是一个度分布为(3, 6)LDPC码原模图单元，其中V代表变量节点，C代表校验节点。将单原模图复制L次，如图1(b)所示，形成耦合长度为L的原模图序列，t为原模图序列的起始时刻，t+L-1为序列的末尾时刻。图1(c)展示了边缘扩展的过程，将t时刻原模图的边端变量节点连接到位置为t,t+1,t+2,···,t+w的检验节点上，w为耦合宽度。图1(d)表示耦合长度为L且w=2时，将图1(b)中每个时刻的单原模图重复图1(c)中边缘扩展后，形成的SC-LDPC原模图链，在原模图链右侧需要额外的w个校验节点终止边缘扩展。

图1 SC-LDPC码原模图的构造过程

单原模图包含Jg个校验节点和Kg个变量节点，其中Jg=J/gcd(J, K),Kg=K/gcd(J, K),gcd(J, K)表示J和K的最大公约数。该原模图对应的矩阵称为基矩阵，大小为Jg×Kg。图1(a)中度分布为(3, 6)单原模图对应的基矩阵为B=[3 3]，对其进行边缘扩展之后，基矩阵被划分为分量基矩阵Bi,i=0,1,2,···,w。图1(c)中耦合宽度w=2时，对应的分量基矩阵B0=B1=B2=[1 1]，将原模图链中的每个单原模图转为矩阵形式排列可以得到SC-LDPC码的基矩阵Bsc，如式(1)所示

将Bsc中“1”和“0”分别替换为M0×M0的单位循环移位矩阵和M0×M0的全零矩阵，M0定义为扩展因子，可得到SC-LDPC码的奇偶校验矩阵Hsc，大小为(L+w)JgM0×LKgM0。该方法生成的SC-LDPC码的码率RL，如式(2)所示

3 SC-LDPC码滑窗译码和错误传播现象

LDPC码常用的译码方法为BP译码，将接收到的码字信息在变量节点和校验节点之间迭代更新，直到满足奇偶校验方程或者达到最大迭代次数。由于SC-LDPC码的奇偶校验矩阵具有对角带结构，可以在尺寸为W的窗口内运行BP译码[16]，其中W为窗口大小，w+1≤W≤L, W∈Z+。

图2展示了滑窗译码过程，即SWD算法。窗口矩阵HWD的校验节点数量为W×Jg×M0，变量节点数量为W×Kg×M0，窗口尺寸为W JgM0×WKgM0。首先窗口矩阵位于校验矩阵左上角，在整个窗口内执行BP译码，在整个窗口译码结束后只输出目标符号，目标符号译码完成之后，整个窗口向右下方滑动JgM0行和KgM0列，在下一个窗口内继续对目标符号进行译码，直到译码窗口移出校验矩阵。

图2 SC-LDPC码滑窗译码

在SC-LDPC码中，由于原模图链中相邻的w个原模图单元具有耦合关系，即目标符号的校验节点与相邻原模图的部分信息节点相连，因此每个窗口内目标符号的信息更新受到前续窗口译码时关联边信息的影响，相关的边信息也将参与每个窗口的奇偶校验判断。

图3为w=2的窗口译码示意图，编号①的码块信息是来自时刻p的窗口的输出对数似然比，该码块将作为目标符号相关信息参与到第p+1时刻窗口的译码中。依据耦合宽度w的取值，第p时刻的码块信息将会对连续w个时刻窗口译码产生影响，因此如果当前窗口未能译码成功，不可靠的目标符号的判决对数似然比信息会传递到后续的w个窗口中从而可能触发一系列码块的译码错误，这种现象称为滑窗译码的错误传播[11]。在这种情况下，错误传播在窗与窗之间有可能引发“译码失控”，产生“爆炸式”的译码错误。

图3 滑窗译码中的错误传播

下面介绍两种SC-LDPC码滑窗译码算法的优化算法，本文所提算法将与其进行对比。

SWD算法将目标符号接收先前窗口的判决对数似然比作为目标符号相关信息参与当前窗口译码。文献[10]中提出消息复用滑窗译码(MR-SWD)算法，将先前窗口的边信息(非判决信息)作为只读数据参与当前窗口译码。当窗口位置滑动离开初始位置后，窗口仅对新进入窗口的区域初始化，且目标符号相关信息位置开始接收先前窗口保留的只读边信息对数似然比。

SWD算法中窗口尺寸固定不变，文献[13]提出窗口扩展滑窗译码(WE-SWD)算法，根据目标符号的平均对数似然比调节窗口大小。首先设置窗口初始大小Wmin和窗口最大值Wmax，定义阈值θ为码字在特定信噪比所有窗口从初始值Wmin到最大值Wmax计算出的对数似然比累计平均值。如果计算出的目标符号对数似然比小于阈值θ，则递增当前窗口大小并重新开始迭代译码，重复该过程直到目标符号满足阈值条件或者窗口大小达到预设最大值。

4 SC-LDPC码残差滑窗译码算法

在信息传输过程中，由于受噪声和干扰的影响，接收序列中会出现一些可靠性较低的节点，这些节点可能导致译码算法难以收敛。在某种意义上，可靠性较低的节点比可靠性较高的节点更需要接收新的有用信息以便完成正确的判决[17]。在一个窗口内并不是所有的信息更新对实现译码收敛都具有相同的作用，更新前后差异较小的边信息值对译码收敛几乎是冗余的，且对译码性能提升几乎无益，优先更新迭代前后差异较大的边信息更有助于译码收敛和提高译码效率。本文提出的RSWD算法，通过动态选择窗口内可靠度最低的边信息优先传输，降低边信息无效更新的频率，加快窗口内译码的收敛速度，提高译码效率，减少译码平均迭代次数，从而提高译码性能和降低整体译码时延。

RSWD算法将边信息更新前后的变化量称为残差，用于筛选窗内边信息更新的优先级，如式(3)所示

假设有码字序列X=[x1,x2,...,xn]，其中n表示码长，经二进制相移键控(Binary Phase Shift Keying, BPSK)调制后，经加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道传输，接收序列表示为Y=[y1,y2,...,yn]，对接收序列进行RSWD算法译码，其具体步骤描述如下：

步骤1 参数设置。输入扩展因子M0、窗口尺寸W、迭代上限I和耦合长度L。

步骤2 窗口初始化。当窗口位于校验矩阵左上角(p=1)时，基于接收序列对译码窗口进行边信息初始化，初始化信息的计算如式(4)、式(5)所示，其中Vj表示当前窗口第j个变量节点，rVj表示第j个变量节点接收的信道观测值，MVj→Ci表示第j个变量节点传递给第i个校验节点的边信息，E和HR矩阵均初始化为全0矩阵

当窗口开始滑动(p＞1)后，如图2所示，对新进入窗口信息窗口右下角区域初始化(黄色的信息块)，目标符号信息位接收前一窗口的输出对数似然比LLR。

步骤3 迭代译码。根据式(3)在窗口内计算残差矩阵HR，并搜索HR获得最大残差值对应的校验节点Ci和变量节点Vj，更新边信息ECi→Vj并对该边信息的残差值更新置0，分别如式(6)和式(7)所示，i→Vj表示第l次迭代中第i个校验节点传递给第j个变量节点的边信息， HRCi→Vj表示更新前后ECi→Vj的残差值，→Ci表示第l次迭代中将第j个变量节点传递给第i个校验节点的边信息，N(Ci)/Vj表示除变量节点Vj外与校验节点Ci相连的变量节点集合

通过式(8)，更新变量节点Vj与相连校验节点Ca{Ca|Ca ∈N(Vj)/Ci} 边信息，N(Vj)/Ci表示除校验节点Ci外与变量节点Vj相连的校验节点集合

通过式(9)，更新校验节点Ca与相连变量节点Vb{Vb|Vb ∈N(Ca)/Vj}所在边信息的残差值

步骤4 译码判决。通过式(10)计算本次迭代结束后的目标符号输出对数似然比，表示第j个变量节点经过l次迭代后输出的对数似然比，xVj表示对的硬判决输出，如式(11)所示

当达到最大迭代次数或者 [xV1,xV2,...,xVj]符合奇偶校验，则当前窗口内停止迭代，并输出判决结果；否则返回步骤3继续译码。

步骤5 窗口滑动。当译码窗口完成当前目标符号译码后，输出目标符号译码结果，窗口向右下方滑动JgM0行和KgM0列，然后返回步骤2，译码下一个目标符号。

上述译码流程中，由于当前窗口目标符号的译码结果将传递给后续窗口，其判定结果会影响后续目标符号的译码准确性。因此如果在达到最大的译码迭代次数后仍无法满足奇偶校验，不可靠的信息会导致当前窗口目标符号译码失败，亦或传递给后续窗口，导致各窗口输出的目标符号误码率上升。RSWD算法根据残差确定信息更新的优先顺序，在当前窗口内选择可靠度最低的边信息优先更新，从初始窗口译码目标符号开始时就可减少不可靠信息传递概率。当窗口滑动有新的信息进入窗口时，与前窗口传入的边信息相比，新进入窗口的边信息残差值较大，有助于窗口将译码重心侧重到新入信息，提高了窗口内边信息更新的精准性和窗口输出的可靠性，能够抑制滑窗译码中错误传播现象。

为验证残差译码的有效性，图4展示了码长为714、耦合长度L为24、窗口大小W为8、信噪比为4 dB的RSWD算法和SWD算法在窗口各位置的误码率(Bit Error Ratio, BER)曲线。由图可知，窗口中每个位置RSWD算法的误码率均优于SWD算法，在窗口内使用残差译码能够有效抑制错误传播。

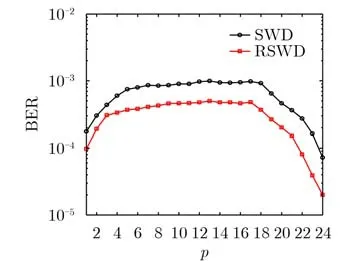
图4 SWD算法和RSWD算法窗口各位置的误码率比较

5 仿真分析

图5展示了本文仿真所使用的SC-LDPC码校验矩阵。如无特殊说明，仿真采用码长714、码率为0.625、耦合长度L为24、耦合宽度w为3、扩展因子M0为7的矩阵，即单位矩阵为7×7的SC-LDPC码，矩阵内阴影部分的数字表示单位矩阵循环右移的位数。仿真采用BPSK调制，基于AWGN信道。

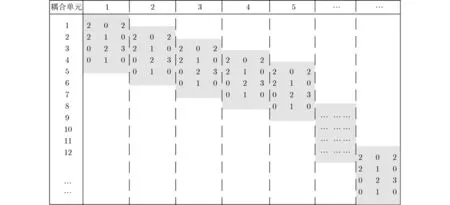
图5 仿真使用的SC-LDPC码校验矩阵

图6给出了所提RSWD算法同SWD算法、MRSWD算法和MR-RSWD算法在窗口大小为8，最大迭代次数为50次时误码率曲线，MR-RSWD算法是在MR-SWD算法基础上引入残差所得。由图可知，引入残差的消息复用滑窗译码(MR-RSWD)算法性能最优异，残差滑窗译码(RSWD)算法性能优于消息复用滑窗译码(MR-SWD)算法和滑窗译码(SWD)算法。在误码率为10-5时，SWD算法信噪比需要大约4.96 dB, MR-SWD算法需要约4.91 dB, RSWD算法需要约4.78 dB，而消息复用下的RSWD算法(MR-RSWD)需要4.72 dB，相较于滑窗译码、消息复用下滑窗译码、残差滑窗译码分别提升约0.24 dB, 0.19 dB, 0.06 dB。

图6 SWD算法、MR-SWD算法、RSWD算法和MR-RSWD算法译码性能比较

图7给出了4种算法在信噪比分别为4 dB和5 dB时译码性能与最大迭代次数的关系。如图7所示，MR-RSWD算法为达到相同误码率，所需迭代次数最少，其次是RSWD算法。在信噪比为5 dB、BER为10-5量级时，SWD算法、MR-SWD算法需30次迭代，而RSWD算法、MR-RSWD算法仅需15次迭代，在同等误码率情况下，引入残差可有效降低译码迭代次数，文献[10]所提MR-SWD算法和MR-RSWD算法在最大迭代次数30和20次之前时性能相较于SWD算法和RSWD算法有所下降。

图7 最大迭代次数对SWD算法、MR-SWD算法、RSWD算法和MR-RSWD算法误码率性能的影响

图8给出了所提RSWD算法同SWD算法和WESWD算法误码率性能比较，其中初始窗口大小Wmin为8，最大窗口Wmax为10，最大迭代次数为50，WE-RSWD曲线是在WE-SWD算法的基础上引入残差所得。由图可见，WE-RSWD算法性能优势明显，RSWD算法和WE-SWD算法在中低信噪比下性能接近，在信噪比4 ～5 dB，RSWD算法译码性能略差于WE-RSWD算法。在BER为10-5量级时，WE-RSWD算法相较于SWD算法、RSWD算法和WE-SWD算法分别有0.45 dB, 0.24 dB和0.18 dB性能优势。

图8 SWD算法、WE-SWD算法、RSWD算法和WE-RSWD算法译码性能比较

图9所示为在信噪比为4.5 dB下，最大迭代次数对不同算法误码率性能的影响。由图可见，本文所提算法有明显的瀑布区，随着迭代次数增多，RSWD算法和WE-SWD算法误码曲线下降迅速，WERSWD算法误码率性能优于其余算法。在误码率为7×10-5时，SWD算法、RSWD算法、WE-SWD算法和WE-RSWD算法所需迭代次数约为50次、18次、14次和8次可达相同的误码性能。综合上述仿真结果，通过引入残差可以有效提高滑窗译码及其他窗译码算法的译码性能，减少平均译码迭代次数，降低整体译码时延。

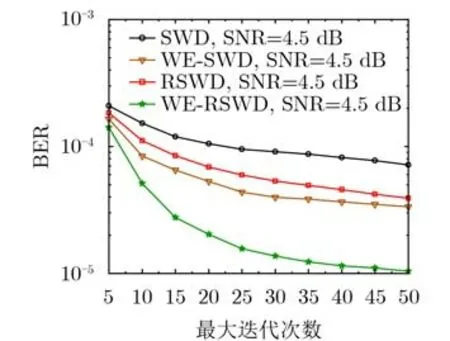
图9 最大迭代次数对SWD算法、WE-SWD算法、RSWD算法和WE-RSWD算法误码率性能的影响

窗口译码的复杂度与译码的迭代次数有关，文献[18]提出滑窗译码复杂度C，表示为C=Ii×W。其中N为窗口滑动的次数，Ii表示为第i个窗口译码结束所需的平均迭代次数，W为窗口大小。如图10所示，对比了6种算法译码复杂度。由图10可见，对比RSWD算法、SWD算法、MR-SWD算法和WE-SWD算法，WE-SWD算法译码复杂度最高，原因在于其译码过程中增加了窗口的尺寸。由于在残差滑窗译码算法中，需要计算窗口内残差值大小再进行信息传递，因此在SWD算法、MRSWD算法和WE-SWD算法的基础上增加残差算法，复杂度略有上升，在信噪比为3 dB和3.5 dB时复杂度增加约11%和15%，随着信噪比升高，整体译码算法的复杂度会降低。

图10 滑窗译码算法复杂度

6 结束语

针对空间耦合LDPC码滑窗译码中错误传播导致的高误码率问题，该文提出基于动态残差的滑窗译码算法。该算法利用残差值的方式筛选掉窗口内冗余的信息，在窗口内选择最大残差所在的边优先更新，降低边信息无效更新的频率，提高译码误码率性能，减少译码平均迭代次数，提高窗口内译码收敛速度。仿真结果表明，在高信噪比区域或者低迭代次数的情况下，RSWD算法的误码率性能均优于SWD算法；将动态残差应用到传统滑窗译码、消息复用滑窗译码和窗口扩展滑窗译码3种窗译码算法中，可以有效地提升窗译码性能和减少平均迭代次数，抑制错误传播效果明显且复杂度增加不大。