考虑双重剪切的开放系统梯形渠道Pasternak双参数冻土地基梁模型

肖 旻，王正中，吴 浪，杨晓松，崔 浩，葛建锐

(1.江西科技师范大学建筑工程学院，江西，南昌 330013；2.西北农林科技大学旱区寒区水工程安全研究中心，陕西，咸阳 712100；3.西北农林科技大学旱区农业水土工程教育部重点实验室，陕西，咸阳 712100；4.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃，兰州 730000；5.塔里木大学水利与建筑工程学院，新疆维吾尔自治区，阿拉尔 843300；6.兰州理工大学能源与动力工程学院，甘肃，兰州 730050)

在中国北方广大旱寒地区，渠系灌溉是维系农业发展的主要灌溉方式，但冬季极易发生冻害[1]。众多学者对冻土冻胀特征、渠道冻害机理及冻胀力学模型进行探索[2-6]。李甲林等[7]通过分析梯形渠道冻害机理，初步明确冻胀条件下衬砌承受的荷载类型并提出梯形渠道冻胀力学理论框架。申向东等[8]将板间填缝视为铰结点并提出预制板衬砌梯形渠道冻胀力学模型。宋玲等[9]把冬季输水渠道冻胀力学分析视为非垂直、非全周冻拔问题，建立冬季输水梯形渠道冻胀力学分析框架。唐少容等[10]提出小U 形渠道冻胀力学分析方法。此类模型因未考虑冻土-衬砌间相互作用即未考虑冻胀力随衬砌冻胀变形发生的释放与衰减现象，计算结果往往偏保守。

弹性地基梁模型是研究土体-结构间相互作用的行之有效、应用广泛的方法[11-15]，已在寒区工程力学分析中得到广泛应用[16-19]。就渠道而言，李宗利等[20]提出“冻胀力系数”的概念并构建基于Winkler 模型的梯形渠道冻胀力学理论框架。肖旻等[21]构建考虑冻土-结构间相互作用的梯形渠道Winkler 地基模型。何鹏飞等[22]基于冻胀力与切向冻结力的关系对文献[21]进行修正，指出强度校核时应考虑切向冻结力的影响。葛建锐等[23]基于Winkler 模型对结冰初期-流冰期-封冻期三个阶段分别构建了考虑冰-结构-冻土协同作用的梯形渠道冻胀破坏弹性地基梁模型。

由此可见，相关研究已取得一定进展，但仍存在一些问题：首先，Winkler 模型本身存在固有缺陷，它忽略土中剪力即没有考虑离散土弹簧间的相互作用，而因冰胶结作用冻土剪切系数普遍大于常温土，这将影响结果准确性[11-12,24-26]。其次，已有模型常预先假定切向冻结力分布规律(如假定切向冻结力呈线性分布、切向冻结力与法向冻胀力成正比或接触面各点同时达到屈服强度等)，这些假定与实际不尽相符。若该分布能从模型中自然导出从而避免预先假定，将有助于进一步提高模型的合理性和完备性。

为此，该文在现有模型基础上，类比常温土双参数模型，引入仅产生剪切变形但不可压缩的剪切层使土弹簧相互联系，用两个参数描述土体特性，体现土体变形的连续性。在冻土-衬砌接触界面引入切向Winkler 弹簧构建以各截面切向位移为基本未知量的平衡微分方程并求解，可避免预先假定切向冻结力分布。

1 模型的建立

冻土-结构间法向相互作用包括两个方面：冻土冻胀受到衬砌板约束产生冻胀力，同时衬砌发生冻胀变形；衬砌变形使其对冻土冻胀的约束减弱，导致冻胀力消减与释放，当冻土-衬砌间有脱离趋势时转为法向冻结力(两者合称接触面法向应力)[27-28]。

冻土-结构间切向相互作用指冻土-衬砌接触面有相对滑移趋势时引起的约束反力。

1.1 基本假设

地下水埋深浅导致冻结过程中存在明显水分补给的渠道称开放系统渠道[21,29]。本文以此类渠道为研究对象，对具体渠道而言地下水补给视为引起冻土冻胀强度差异的主导因素[21,30-31]。

结合已有研究[7-10,20-23]，补充如下假设：

1) 渠道沿输水方向尺寸远大于横向尺寸，力学分析简化为平面应变问题。

2) 力学分析仅考虑冻深范围内冻土层变形，不考虑冻深以外土层的固结。

3) 把渠基土等效为考虑双重剪切的双参数地基(如图1)。引入Pasternak 剪切层描述冻土-结构间法向相互作用；引入满足Winkler 假设的接触界面层描述冻土-结构间的切向相互作用。

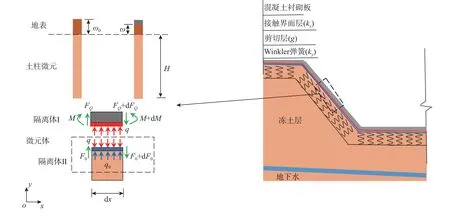
图1 考虑双重剪切的Pasternak 冻土地基梯形渠道断面示意图Fig.1 Section of trapezoidal canal on Pasternak frozen soil foundation considering double shear effect

下标i为e时代表底板，为t时泛指坡板，分别为m、s时特指阴、阳坡坡板。接触面法向应力表现为冻胀力时取正值，表现为冻结力时取负值。图1 为断面示意图。ω0为自由冻胀量；ω为实际冻胀量；H为冻深；q0为作用在剪切层上的接触面法向应力；q为作用在衬砌板上实际的接触面法向应力；F0为作用在剪切层上的剪力；FQ为作用在衬砌板上的剪力；M为截面弯矩；kx为接触面切向刚度；ky为基床系数；g为剪切系数。图1 中坡板采用的坐标系以渠顶为原点，x轴正向由渠顶指向渠底，y轴正向垂直坡面指向渠槽一侧；底板采用的坐标系以左侧坡脚为原点，x轴正向自左侧坡脚指向另一侧坡脚，y轴正向垂直底面朝上。

1.2 冻土-衬砌法向相互作用的控制方程

1.2.1 渠道基土自由冻胀量

中国北部多数省区有关部门都设置试验场确定冻土冻胀强度与地下水位的函数关系[7,30,32-33]。研究表明[7,20-23,30-35]，该函数关系可表达如下：

式中：η0为自由冻胀强度；z为地下水位；a、b为经验系数。

考虑到地下水位的横向差异，有各点自由冻胀量如下[7,20-23,30-35]：

1.2.2 接触面法向应力计算

冻土自由冻胀量被完全约束时，结构处于未变形的初始状态，剪切层也处于未变形且无内力的初始状态，此时衬砌板受到的冻胀力可视为初始外荷载。但工程中基土冻胀并不会被完全约束，往往处于部分约束状态，此时结构对冻土约束程度降低，导致冻胀力的衰减与释放，可以认为产生一个与衬砌板冻胀位移成比例的附加荷载使冻胀力减小[21](即冻胀力线性衰减，小变形条件下符合实际)，同时考虑剪切层挠曲引起剪力F0的修正。最后，冻土-结构间相互作用趋于平衡，此时荷载分布为实际的接触面法向应力分布。

首先，计算作用在剪切层上的接触面法向应力q0(x)。由于此时仅考虑Winkler 弹簧变形尚未计入剪切层的影响，从而可参考已有文献[7, 20 - 23, 31]，并注意到冻土与衬砌间变形协调即衬砌板与剪切层在对应点挠度相同，q0(x)可由式(3)计算：

式中：Ef为冻土弹性模量；ω(x)为实际冻胀位移；p(x)为初始外荷载。类比常温土弹性地基梁模型[36]，系数Ef/H可视为基床系数，即ky=Ef/H。式(3)中右侧第二项反映衬砌冻胀变形引起的冻胀力释放和衰减。

其次，计算实际接触面法向应力q(x)。如图1所示。取隔离体Ⅱ为分析对象，同时由沿法向(即y轴方向)的静力平衡条件有：

考虑到F0(x)=-g·dω(x)/dx，其中g为剪切系数，负号表明ω′(x)与F0(x)符号相反。依据式(4)，接触面法向应力分布q(x)如下：

1.2.3 渠道衬砌冻胀变形的挠曲线微分方程

类比常温土Pasternak 弹性地基梁理论[11-12,24-26]，取图1 中隔离体Ⅰ为研究对象，可导出挠曲线微分方程如下：

式中：Ec为混凝土的弹性模量；I为惯性矩。

剪切系数可依据VLASOV 等[37]的方法确定，计算公式为：gi=(Efi·Hi)/[6·(1+ν)]，其中Ef为基土弹性模量；Hi取冻土层厚度；ν为泊松比。

考 虑 到pi(x)=0.01Efi·a·e-bz(x)[19-21,29,36]，代 入式(6)整理并化为标准形式如下：

式中：

渠道底板与坡板的受力特点如图2 所示，底板两端同时受坡板约束；坡板则在坡顶处受顶盖板约束，在坡脚处受到底板约束。设le为底板板长，be为底板板厚；lt为坡板板长，bt为坡板板厚。

图2 梯形渠道衬砌板的冻胀破坏及端部约束示意图Fig.2 Frost-heaving damage and end restraints of concrete lining of trapezoidal canals

因底板各点到地下水埋深的距离相同，式(7)中右侧为均布荷载。设渠顶地下水位为z0，断面深度为h，则z(x)恒等于z0-h。将z(x)代入式(7)得底板挠曲线微分方程如式(8)。坡板各点到地下水埋深的距离不同，从而式(6)中右侧为非均布荷载。由几何关系有：z(x)=z0-x·sinθ，其中θ/(°)为坡板倾角。将z(x)代入式(7)得坡板挠曲线微分方程如式(9)。式(8)、式(9)共同组成冻土-衬砌法向相互作用的控制方程。

1.3 冻土-衬砌切向相互作用的控制方程

1.3.1 坡顶法向约束力及板间相互作用力

冻土与衬砌板接触面切向相对滑移趋势主要源于冻胀力作用下坡板、底板、顶盖板间的相互作用。因此，应求解顶盖板对坡板的约束力及板间相互作用力，如图3 所示。图中：s 为阳坡；m 为阴坡；e 为渠底。共有9 个未知量：阴、阳坡坡顶法向约束力NAm、NAs；阴坡与底板相互作用力NBm、NCm；阳坡与底板相互作用力NBs、NCs；坡板、底板底部受到的切向冻结力分布τm(x)、τs(x)、τe(x)。

图3 各衬砌板约束力及板间相互作用力示意图Fig.3 Constraining forces and interaction forces between concrete lining plates of trapezoidal canal

由坡板静力平衡可得(因衬砌为薄板结构，忽略切向冻结力对各截面形心的弯矩)：

因NCm、NCs通常为压力，取预设方向为负。根据底板静力平衡有：

联立式(10)、式(11)可解出除τm(x)、τs(x)、τe(x)以外剩余的6 个未知量。

1.3.2 渠道坡板各截面切向位移及切向冻结力

以阴坡坡板为例推导以切向控制方程。解出切向位移um(x)后，根据Winkler 假设可确定切向冻结力分布τm(x)。

此处切向冻结力指NCm作用下冻土-结构间有相对滑移趋势时引起的切向约束力，计算τm(x)时仅考虑顶托力NCm作用，不考虑板自身弯曲影响。将渠坡衬砌视为侧边承受轴向力的同时界面受到切向约束的矩形梁，如图4。NCm作用下切向冻结力自渠顶指向坡脚。因渠道为薄板结构，截面应力视为均匀分布[38-39]，下同。

图4 渠道坡板切向冻结力分布计算简图Fig.4 Schematic diagram for calculation of distribution of tangential ad-freezing force on slope plate

考虑图4 右侧所示长度为dx的微元体，σm(x)为截面应力，由x轴方向的静力平衡条件有：

设阴坡板各截面切向位移为um(x)，依应力、应变与位移本构关系有：σm(x)=Ec·[dum(x)/dx]，同时有：dσm(x)/dx=Ec·[d2um(x)/dx2]。接触界面服从Winkler 假设，从而切向约束力τm(x)大小与um(x)成正比但方向相反，即：τm(x)=-kxm·um(x)，kxm为切向刚度。结合式(12)，得到以截面切向位移为基本未知量的微分控制方程：

式(13)为齐次方程，其通解为：

式中：cm1、cm2为待定常数；sinh、cosh 为双曲函数。该式应满足如下边界条件：考虑顶盖板约束作用，当x=0 时，um(0)=0；当x=lt时，σm(lt)=NCm/bt。又NCm已先行解出，方程得解。将该方程的解代入“τm(x)=-kxm·um(x)”即得渠道坡板切向冻结力分布。

1.3.3 渠道底板各截面切向位移及切向冻结力

渠道底板切向冻结力指底板两端板间相互作用力水平分量Nmx=NCm·cosθ-NBm·sinθ 及Nsx=NCs·cosθ -NBs·sinθ 同时作用下冻土-结构间有相对滑动趋势时导致的约束反力，同样在计算τe(x)时仅考虑底板两侧板间相互作用力的影响。将底板视为两端承受轴向集中力的同时接触界面受到切向约束的矩形梁，如图5 所示。由于阴坡、阳坡板对底板作用力有差异，切向约束力应自阳坡一端指向底板另一端。应用与第1.3.2 节相同的方法，可导出底板切向冻结力分布。但需要注意的是，此时应采用如下边界条件：当x=0 时，σe(0)=Nmx/be；同时当x=le时，σe(le)=Nsx/be。

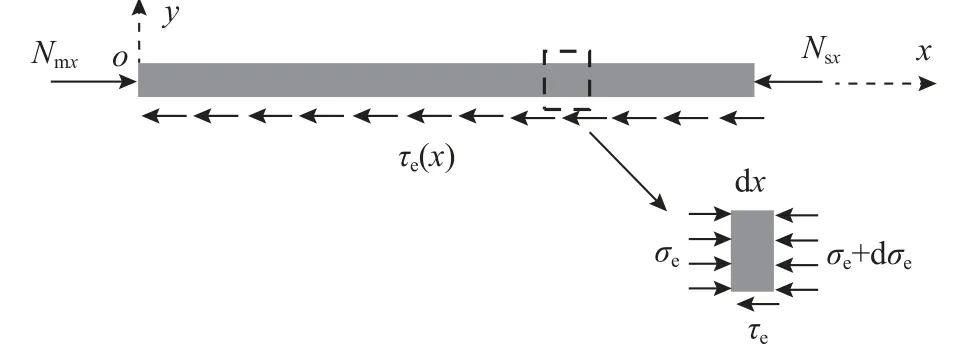
图5 渠道底板切向冻结力分布计算简图Fig.5 Schematic diagram for calculation of distribution of tangential ad-freezing force on bottom plate

2 模型的求解

2.1 法向控制方程的求解

因式(7)、式(8)、式(9)三者齐次方程形式相同，故先确定方程的齐次解。以阴坡坡板为例，将式(9)齐次化，则其特征方程如下：

式中，r为待定系数。式(15)的判别式为：Δm=。根据ρm不同可分以下3 种情况：

1) ρm<1，即Δm<0 时，式(9)齐次解ωmh(x)为：

其中，基函数矢量F1及任意常数矢量C为：

式中：

2) ρm=1，即Δm=0 时，易知φm2=0，此时式(9)的齐次解ωmh(x)如下：

式中，基函数矢量F2为：

3) ρm＞1，即Δm＞0 时，式(9)的齐次解如下：

其中，基函数矢量F3为：

对阴坡板而言，式(9)存在特解ωmn(x)如下：

其中：

结合齐次解与特解，可得其通解为：

可根据如下边界条件确定任意常数：当x=0时，ωm(0)=0，(0)=0；当x=lt时，ωm(lt)=0，(lt)=0。阳坡坡板的情形与阴坡类似。对渠底板而言，式(8)的齐次解ωeh(x)与坡板相同。

此外，式(8)还存在特解ωen(x)如下：

结合齐次解与特解，可得其通解为：

可根据如下边界条件确定任意常数：当x=0 时，ωe(0)=0，′(0)=0；当x=le时，ωe(le)=0，(le)=0。

2.2 计算流程

根据前述分析，可归纳计算流程如下：

1) 参数选取。可进行试验或根据相关文献获取参数。其中参数a、b反映除地下水补给条件外特定地区具体工程所在区域气象、土质等其他因素的综合影响，条件允许时应拟合当地试验数据获取，相关文献[7, 20 - 23, 30 - 35, 40 - 41]提供了部分地区部分土质下的结果可供参考；冻土剪切系数g由Vlasov 提供的方法确定[37]；冻土-混凝土界面切向刚度kx可实施剪切试验拟合切向应力-相对切向位移函数关系获取。

2) 依据特征方程式(15)的判别式Δi并通过式(16)～式(18)可分别确定阴坡、阳坡及渠底衬砌板法向控制方程齐次解，再依据式(19)、式(21)可确定方程特解。结合齐次解与特解，引入边界条件求解方程组可得阴、阳坡板及底板冻胀变形ωm(x)、ωs(x)、ωe(x)。

3) 将ωm(x)、ωs(x)、ωe(x)代入式(5)，可得阴坡、阳坡及渠底板的接触面法向应力分布qm(x)、qs(x)、qe(x)。将qm(x)、qs(x)、qe(x)作用到结构上可对渠顶法向约束力及衬砌板间相互作用力进行计算，即联立式(10)、式(11)可得坡顶法向约束力NAm、NAs及板间相互作用力NBm、NCm、NBs、NCs。

4) 在此基础上，求解式(13)可得阴、阳坡板和底板各处切向位移um(x)、us(x)、ue(x)，进而可得切向冻结力τm(x)、τs(x)、τe(x)。

5) 仍以阴坡坡板为例，各截面内力如下式：

式中：Mm(x)为阴坡板截面弯矩；Nm(x)为阴坡坡板截面轴力。y轴方向以垂直衬砌指向渠槽一侧为正。

渠道底板各截面内力如下式：

6) 至此，由工程力学方法可进行抗裂验算。

3 算例分析

塔里木灌区[40-41]位于天山南麓、塔里木盆地西北缘。最低气温为-29.3 ℃，历年负温天数为75 d。有塔里木河、阿克苏新大河和田河等五大河流贯穿，建有多浪、胜利、上游三大水库，地表水及地下水资源丰富。地下水埋深浅，地下水补给是基土冻胀的主导因素。

以该灌区某梯形渠道为例。衬砌板厚为0.08 m，采用C15 混凝土衬砌，基土土质为轻壤土。底板长le为2 m，坡角为45°，断面深度为2.5 m，地下水埋深(至渠顶)约3.5 m。作者团队于2010 年-2011 年冬季开展原型观测[40-41]。坡板隔50 cm 设测点；底板隔25 cm 设测点。以保证刚度、稳定性为原则布设监测设备，设置位移计测冻胀位移，并用水准仪校正。Ec取22 GPa；a取21.972，b取0.022，其余参数见表1。

3.1 衬砌板冻胀变形计算与对比分析

依计算流程求解法向控制方程式(8)、式(9)可得阴坡、阳坡及渠底衬砌板冻胀位移曲线ωm(x)、ωs(x)、ωe(x)。图6 为阴坡坡板及底板冻胀位移曲线，包括依据本文模型(Pasternak 模型即g≠0)、Winkler 模型(g=0)、材料力学方法的计算结果以及观测值。

图6 阴坡与渠底衬砌板的冻胀位移曲线Fig.6 Frost-heaving induced displacement of each section of both shady and bottom lining plates

由图6 可知，三种方法计算的冻胀位移分布均能较好地反映原型渠道冻胀变形总体趋势。其中材料力学方法因未考虑衬砌冻胀变形引起冻胀力的释放与衰减，结果与观测值相比偏大、偏保守。弹性地基梁模型因考虑了冻土与衬砌间相互作用，计算结果精度整体优于材料力学方法，与观测值符合良好，且本文模型结果较Winkler 模型更接近观测值。这是因为，双参数模型引入Pasternak剪切层考虑了独立土弹簧间相互作用，提高了模型计算精度，使计算结果更符合实际。当剪切系数g=0 时，本文模型可退化为Winkler 模型。

考虑到顶盖板约束及坡脚处板间的相互约束，本文将衬砌两端法向冻胀位移为0 作为控制方程的边界条件。而实际上，各衬砌板两端观测值并不是准确为0，顶盖板及坡脚处因冻土冻胀发生了松动。这将导致一定偏差，但偏差不显著。

3.2 接触面法向应力分布

把冻胀位移ωm(x)、ωs(x)、ωe(x)代入式(5)得接触面法向应力分布qm(x)、qs(x)、qe(x)，如图7所示。图7 中，数值为正时表示法向冻胀力，为负表示法向冻结力。由图7 可见，接触面法向应力相对假设自由冻胀量被完全约束的情形(即初始冻胀力)表现出一定的释放和衰减。例如，底板法向冻胀力分布为中间小、两侧大，正好与冻胀位移分布相反，表明中部因冻胀位移相对较大，冻胀力得到释放，两侧因受到约束冻胀力衰减较小。对阴、阳坡板而言，坡脚受到约束故坡板下部冻胀力衰减较小，又该处初始冻胀力较大，故主要分布法向冻胀力；同时坡板中上部与基土间有相互脱离趋势，又该处初始冻胀力较小，故通常分布法向冻结力；坡顶处则因受到顶盖板约束，衰减较小，又表现为法向冻胀力。接触面法向应力沿断面的总体变化趋势与已有研究基本一致[25-26]。

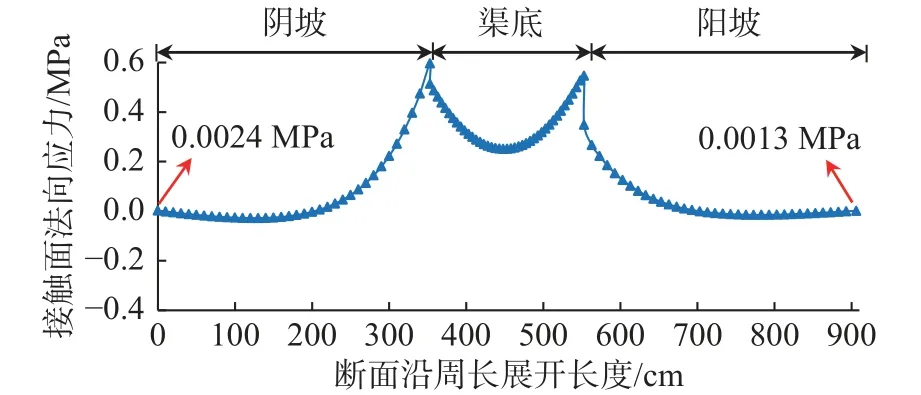
图7 接触面法向应力分布曲线Fig.7 Distribution of normal stress on contact interface between frozen soil and concrete lining

3.3 各截面切向位移分布及易开裂位置估算

把qm(x)、qs(x)、qe(x)作为荷载施加到结构上可对坡顶约束力、板间相互作用力及各衬砌板受到的切向约束力分布τm(x)、τs(x)、τe(x)进行计算；进而可确定衬砌各点截面内力；最后计算各截面上表面应力可进行抗裂验算，并估算最易开裂位置。

以阴坡为例，图8(a)为阴坡板各截面切向位移(绝对值)分布曲线。综合考虑较坚硬及特别坚硬岩土体(如特别坚硬的粘土、冻土、风化岩等)与素混凝土接触面剪切刚度取值范围及本文算例试验值，对剪切刚度kxm(单位：kN/cm3)分别取0.1、0.3、0.5、0.8、1.0 时进行参数分析。由图8(a)可见，当kxm=0.5 时，各截面切向位移(绝对值)从渠顶至渠底逐渐增大，最大值出现在坡脚处，该处被压缩0.629 mm，对照τm-um曲线知仍属弹性粘结区，冻结约束未失效。kxm越小，各截面切向位移趋于线性分布，切向冻结力也趋于线性分布，与已有研究线性分布假设一致[7]；当kxm较大时，各截面切向位移逐渐偏离线性分布，切向冻结力也偏离线性分布且kxm越大偏差越大，此时线性分布假设不再适用。kxm越大即接触面剪切刚度越大，各截面切向位移绝对值总体呈减小趋势。

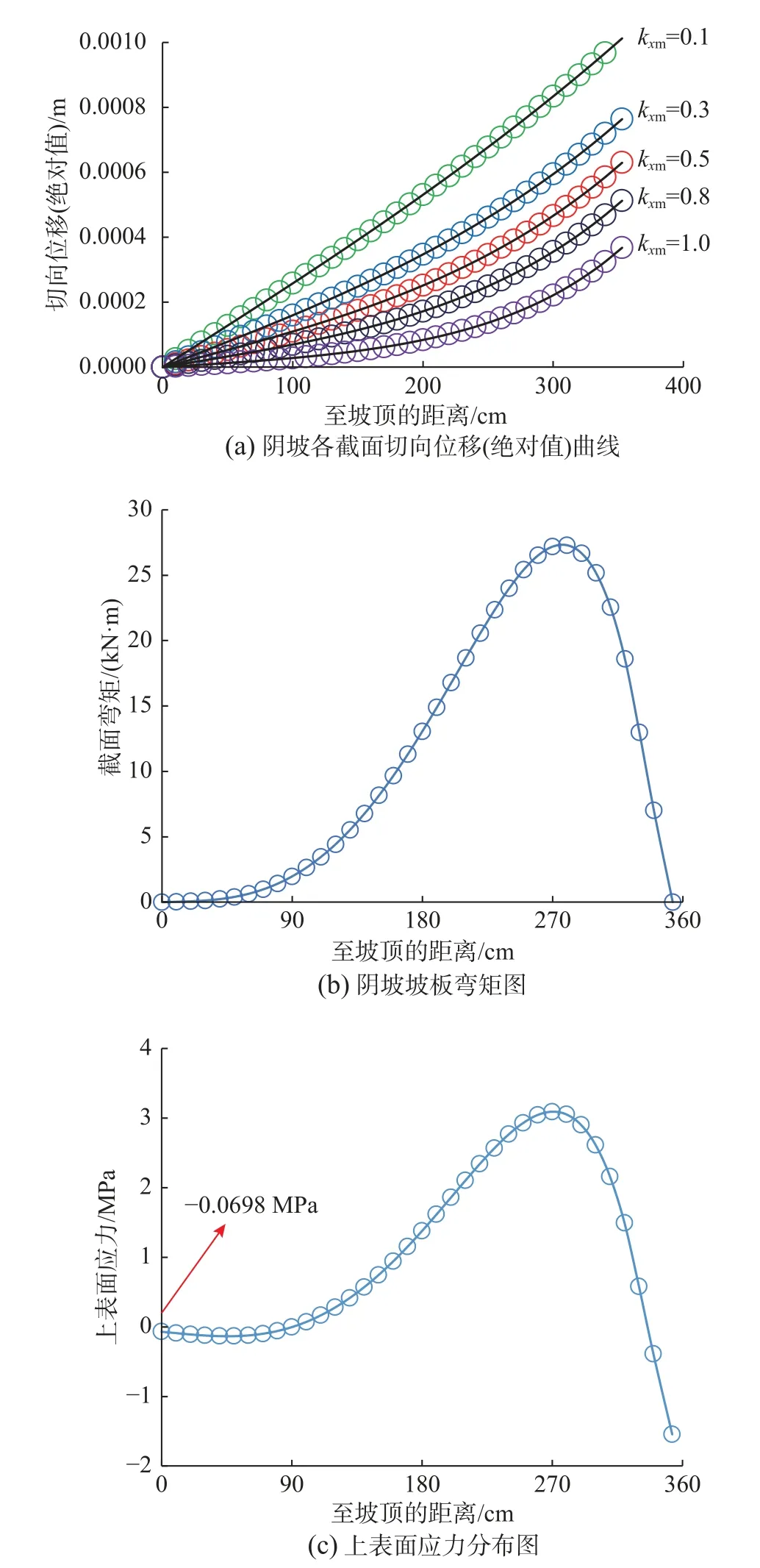
图8 阴坡坡板冻胀力学分析Fig.8 Frost-heaving mechanical analysis of shady slope plate

图8(b)为阴坡坡板弯矩图(凸向渠槽一侧为正)。由图8(b)可知，坡板中下部弯矩较大，靠近坡顶的上部则较小，最大值在距坡脚约1/5 坡板长处，这与已有研究相符[20,27]。弯矩图存在拐点且位置与图8 中阴坡段零点位置一致，位于冻胀力与法向冻结力的交界点，与理论预测相符。同时可见，易导致衬砌板开裂的最大拉应力主要分布在上表面。图8(c)为阴坡各截面上表面应力分布图。由图8(c)可知，因底板顶托及顶盖板约束，坡板两端表现为压应力；坡板中下部为拉应力，最大值在距坡脚约1/4 坡板长处。结合混凝土拉应力允许值，危险截面即易开裂位置在距坡脚约45%～20%坡板长范围内。

笔者课题组对塔里木灌区渠道冻害调查结果表明[40-41]，梯形渠道坡板主裂缝(如图2 所示)易发生范围与本文估算结果基本一致。

3.4 讨论

相对于存在地表或侧向水分补给的特殊情况，地下水补给占主导作用是更加常见的情形。冻土工程中开放系统条件也常特指地下水补给[29]。该模型以开放系统条件下的梯形渠道为研究对象，突出地下水补给的横向差异对渠基土冻胀强度的影响，暂未考虑地表或侧向水分补给，在新疆塔里木灌区、甘肃白银引黄灌区等建有大量此类渠道。此外，如能通过原型观测或者模型试验恰当确定冻胀率分布，则对前两类特殊情形本文方法依然适用。

应用该模型对原型渠道衬砌各点冻胀位移及易开裂位置进行计算，结果与原型观测及灌区调查结果基本相符，表明模型的合理性。与现有结构力学模型相比，本文模型能反映冻土与衬砌结构的相互作用即冻胀力随衬砌冻胀变形的释放和衰减效应，更符合实际；与现有Winkler 模型相比，本文模型通过引入Pasternak 剪切层克服了其未体现土体连续性的不足，引入由切向Winkler 弹簧组成的接触界面层克服了以往需要预先假定切向冻结力分布规律的不足，提高了模型结果的精度。改进的模型能够较好地描述冻土与衬砌板接触面相互作用的基本特征，例如挤压(产生法向冻胀力)、脱开趋势(产生法向冻结力)和粘结滑移(产生切向冻结力)等。

需要说明的是：即使对特定地区的具体工程而言，除地下水补给外，太阳辐射也会产生影响。构建综合考虑水分补给与太阳辐射条件的模型，仍有待深入研究。

4 结论

在现有Winkler 模型基础上，引入Pasternak剪切层反映冻土-结构间法向相互作用，引入切向Winkler 弹簧组成的接触界面层反映冻土-结构间切向相互作用，构建考虑双重剪切的梯形渠道冻土地基梁模型。有以下结论：

(1) 该模型克服已有Winkler 模型未考虑土弹簧间相互作用且需预先假定切向冻结力分布的缺点，有效提高了计算精度，且与事实更加符合。

(2) 以塔里木灌区某梯形渠道为例，对衬砌冻胀变形进行计算，并与材料力学法、Winkler模型计算值及观测值进行对比。结果表明：相比Winkler 模型与材料力学法，本文模型计算值无论在大小还是在总体变化趋势上均与观测值更加一致。当g=0 时退化为Winkler 模型。

(3) 通过参数分析，探讨接触面切向刚度kx对衬砌各点切向位移与切向冻胀力分布的影响。结果表明：当kx越小时，衬砌各点切向位移和切向冻结力越接近于直线分布，与已有研究中采用“上小下大”的三角形分布假设一致；当kx越大，各点切向位移与切向冻结力均不再遵循直线分布规律，此时三角形分布假设不再适用。