Theoretical and numerical research on the dynamic launch response of carbon fiber composite cartridges
Ruijie Zhang, Hui Xu, Chenlei Huang, Kun Liu, Zhilin Wu
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China
Keywords:Composite material cartridges Dynamic response Thick-walled cylinder theory Finite element simulation Toughing-chamber behavior
ABSTRACT Understanding the dynamic response of composite material cartridges during the firing process is of great significance for improving their reliability and safety.A theoretical model describing the dynamic response of composite material cartridges is established based on the thick-walled cylinder theory and rate-dependent constitutive model of composite materials.The correctness of the theoretical model is validated through finite element simulations of cartridge deformation.The influence of chamber pressure and cartridge wall thickness on the cartridge’s deformation process and stress distribution is analyzed.The results indicate that the primary deformation of composite material cartridges inside the chamber is elastic deformation.Compared to metal cartridges, composite material cartridges require higher pressure for touching-chamber and are more prone to developing gaps after unloading to ensure smooth extraction.During the deformation process,the touching-chamber behavior of the cartridge can improve the stress distribution.Under the same chamber pressure, the touching-chamber behavior can reduce the circumferential stress by approximately 30%.The inner wall surface of the cartridge is a critical area that requires attention.The touching-chamber behavior can be facilitated by appropriately reducing the cartridge wall thickness while ensuring overall strength.This study can provide guidance for the optimization design of composite material cartridges.
1.Introduction
Composite materials possess a diverse range of mechanical properties that surpass those of metallic materials, making them highly suitable for use in intricate working conditions while maintaining a low weight.Thus, they are extensively employed in mechanical engineering, aerospace, and the automotive industry[1-5].Furthermore, composite materials have progressively been integrated into cartridges, resulting in a significant decrease in weight [6-9].To ensure the structural design and optimization of cartridges during launch, it is crucial to conduct research on their deformation.A well-constructed cartridge structure can decrease the weight of ammunition while enhancing the cartridge’s launch strength, safety, and reliability.This is particularly significant for the lightweight of weapons and equipment, which improves the carrying capacity of soldiers.
The deformation process of cartridges under chamber pressure during firing can be simplified as that of a composite tube with gaps,exemplified by the expansion deformation of the tube sheet.Bouzid et al.[10,11] utilized thick-walled cylinder theory to determine the deformation and stress properties of plate-tube structures made of elastic-plastic materials,and their calculation results have been verified through experiments and simulations [12,13].Currently, most studies on cartridges’ internal deformation focus on metallic materials.Carlucci et al.[14] analyzed the radial deformation process of cartridges using the composite thin-walled cylinder theory and calculated the minimum radial clearance of cartridges.Parate B A et al.[15] established theoretical and numerical calculation models for the internal pressure deformation process of brass cartridges, and the error between the stress and strain values obtained from theoretical and simulation calculations is approximately 10%.Parate B A et al.[16]analyzed and calculated the stress-strain behavior of brass cartridges subjected to internal pressure by combining the Bilinear and Kinematic hardening models,and experimentally validated the shell’s integrity and ease of extraction.Cai S et al.[17,18] focused on aluminum alloy cartridges and established a deformation model based on the plastic deformation theory of circular tubes.This model considered both the axial deformation of cartridges and the radial constraint of the bottom, and can more accurately predict the form and location of cartridge failure.

Symbols and Interpretation of symbols A, B, C, n, m Material constants in the Johnson-Cook model Er, ERr Elastic moduli in radial direction under quasi-static and dynamic condition (MPa)Eθ, ERθ Elastic moduli in tangential direction under quasistatic and dynamic condition (MPa)Ez, ERz Elastic moduli in axial direction under quasi-static and dynamic condition (MPa)Gθz, GRθz Shear modulus in θ-z directions under quasi-static and dynamic conditions (MPa)Grz, GRrz Shear modulus in r-z directions under quasi-static and dynamic conditions (MPa)Grθ, GRrθ Shear modulus in r-θ directions under quasi-static and dynamic conditions (MPa)h Wall thicknesses of cartridge (mm)P Chamber pressure (MPa)Pc Contact pressure between cartridge and chamber(MPa)ra Inner radius of cartridge body (mm)rb Outer radius of cartridge body (mm)Ra Inner radius of the chamber(mm)Rb The outer radius of the chamber (mm)SF, SC Failure criterion for circumferential fiber tension and radial matrix compression t Time (ms)T* Dimensionless temperature u Deformation of cartridge body (mm)ur1 Deformation of the inner wall surface of cartridges(mm)ur2 Deformation of the outer wall surface of cartridges(mm)δ Radial clearance(mm)ε Plastic strain εr, εθ, εz Strain in radial, circumferential, and axial directions εtθ, εtr Allowable tensile strain in the radial and tangential direction εcr Allowable compress strain in the radial direction ˙ε, ˙εref Strain rate and reference strain rate λEi(˙ε) Correction coefficient for Ei νrθ,νrz,νθz Poisson’s ratio in r-θ, r-z and θ-z directions ρ Density (g·cm-3)σ Stress(MPa)σr,σθ,σz Stress in radial, circumferential, and axial directions(MPa)
For the deformation of composite material cartridges under impact loads, Wang Y X et al.[19] analyzed the deformation and interaction between the inner and outer layers of a double-layered composite explosive cylinder.To simplify the model, they treated the multilayered wrapped fiber composite material as a single layer, and effectively simulated the deformation process of the cylinder under explosion pressure by applying an internal explosive load through a load curve.Wang J G et al.[20,21]used polyethylene as a cartridge for large-caliber ammunition, observed the crack morphology when the cartridge failed, and established a theoretical and simulation model based on the internal deformation of metal cartridges.The failure mode of cartridges was summarized based on static tensile tests and dynamic high-temperature and high-pressure impact tests.However, the model did not consider the changes in the material’s mechanical properties under impact loads.Compared with metal materials,composite materials exhibit more complex mechanical properties due to various modification processes, and the material’s mechanical properties during the dynamic deformation process when the cartridge is subjected to chamber pressure impact differ from those under quasi-static loading conditions during launch.Therefore, it is necessary to establish a targeted model to analyze the deformation patterns of composite material cartridges under chamber pressure.
This paper focuses on continuous carbon fiber-reinforced composite material cartridges and investigates the impact of strain rate on the mechanical properties of composite materials.Combining the thick-walled cylinder theory, a theoretical model for the dynamic deformation of composite material cartridges in chamber is established.The theoretical model considers the influence of strain rate on the mechanical properties of composite material cartridges,and the model is validated by comparing the results with those from finite element simulations.Based on the theoretical and simulation results,the general deformation process of carbon fiber cartridges in the chamber is presented, and the deformation characteristics of cartridges with varying chamber pressure and wall thickness are analyzed.Additionally,the impact of the cartridge-tochamber fit on its deformation and stress is discussed.
2.Theoretical model
2.1.Cartridges and model simplification
This paper focuses on the small caliber cased telescoped ammunition cartridge,which consists of various components such as primer, cartridge, cap, and projectile, as shown in Fig.1.The cartridge is made of carbon fiber wrapped reinforced composite material,with the fiber winding direction at 90°to the canister axis.The wall thickness of the cartridge body is uniform, and there is a curved transition from the inner body to the bottom.
During the process of ammunition firing, the cartridge undergoes expansion and deformation due to the chamber pressure.Fig.2 illustrates how the chamber pressure affects the inner surface of cartridges.The objective of this study is to examine the deformation process of the cartridge body,particularly emphasizing the region with a consistent wall thickness.This specific region can be simplified as the deformation process of a thick-walled cylinder subjected to internal pressure.The cartridge body is a regular cylindrical shell with an inner radius of raand an outer radius of rb.The inner radius of the chamber is Ra,and the outer radius is Rb.In engineering, a specific radial clearance is maintained between the cartridge and the chamber to facilitate ammunition’s smooth supply and discharge.This radial clearance is denoted as δ = Ra- rb.
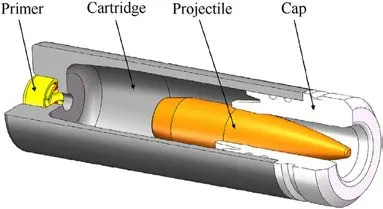
Fig.1.Schematic diagram of small caliber cased telescoped ammunition.
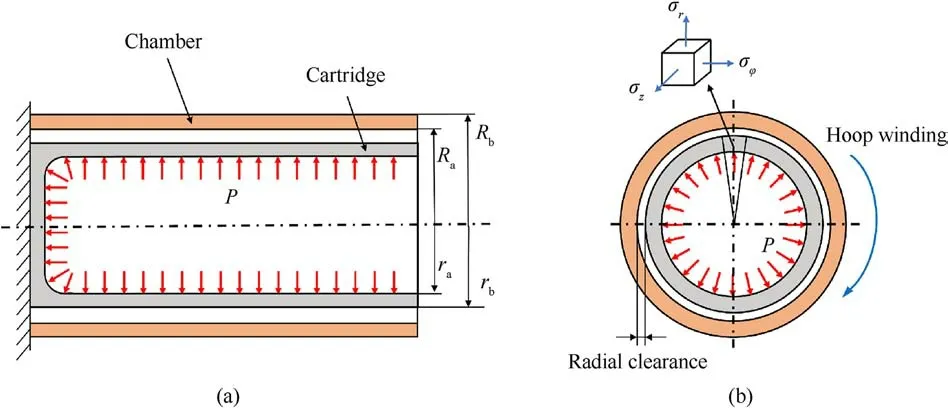
Fig.2.Schematic diagram of in-chamber deformation model of cartridge: (a) Stress diagram; (b) Section of cartridge.
2.2.Constitutive model and rate-dependent correction method
The mechanical properties of continuous fiber reinforced composite materials exhibit orthotropic behavior on a macroscopic scale.In cylindrical coordinates,their stress-strain relationship can be expressed as follows:
where,Er,Eθ,and Ezrepresent the elastic moduli of the material in radial,tangential,and axial directions,respectively,while νrθ,νrz,νθzrepresent the corresponding Poisson’s ratios on the respective planes.Grθ, Grzand Gθzrepresent the corresponding shear moduli on the respective planes.
For orthotropic materials:
During shooting, the cartridge undergoes deformation due to chamber pressure in an extremely short period of time, it is necessary to consider the alterations in the material’s constitutive model when it undergoes impact.Currently, the prevalent approach is to calibrate the constitutive model under dynamic conditions by conducting appropriate dynamic tests, thereby enabling the determination of the alterations in material parameters of composite materials at high strain rates compared to those obtained under quasi-static loading conditions [22,23].
Assuming the modulus matrix under quasi-static conditions:

The dynamic modulus matrix ERof the composite material can be determined based on the strain rate within small time increment Δt, and its stress-strain relationship can be expressed as:
2.3.Dynamic response model of cartridges
During launch,the cartridge is constrained by the chamber and automatic mechanism, and axial deformation is disregarded.As chamber pressure increases, the cartridge undergoes deformation,resulting in a gradual decrease in the radial gap between the cartridge and chamber, as shown in Fig.3(a) Ur1and ur2respectively denote the deformations incurred by the inner and outer wall surfaces of cartridges.
Neglecting the axial stress of the cartridge,according to Eq.(6),the radial strain εrand axial strain εθare:

For a thick-walled cylinder subjected to internal pressure only and neglecting the effects of body force and tangential stress, the radial and circumferential stresses satisfy:
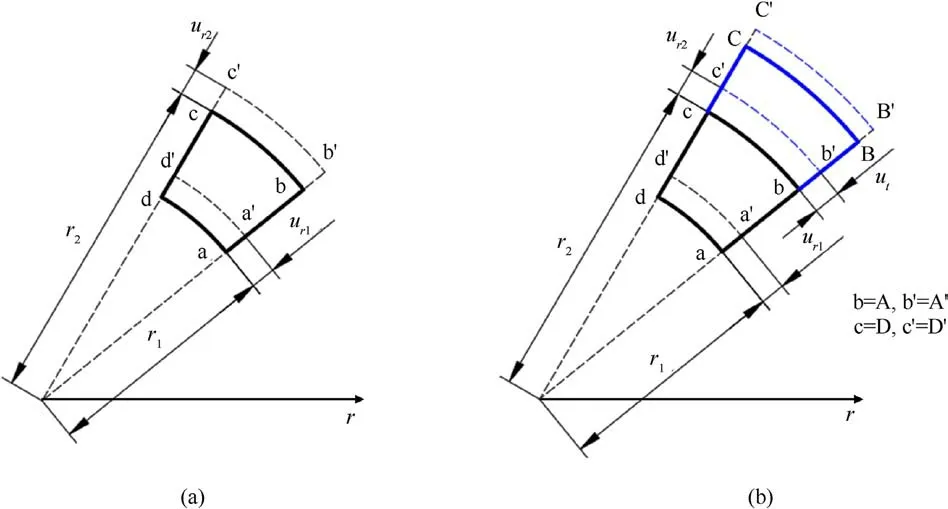
Fig.3.Illustration of cartridge deformation: (a) Before touching chamber; (b) Touching chamber.

Once the cartridge comes into contact with the chamber, both deform under the influence of chamber pressure until the maximum pressure is reached.As shown in Fig.3(b) Utrepresents the deformation generated by the inner wall of chamber.Assuming the contact pressure between the cartridge and chamber is Pc, the radial deformation of the chamber’s inner wall can be expressed as:

As the pressure decreases, the cartridge and chamber will experience a joint rebound.Subsequently, after the chamber has completed its rebound movement, the cartridge will continue to rebound independently until complete unloading is achieved.The deformation process in this section is analogous to the derivation process in the previous section,with the only difference being that the magnitude of the change in chamber pressure is negative in each time step.Further elaboration is deemed unnecessary.
3.Finite element model
Based on the structure of cartridge and chamber, a finite element model for dynamic analysis was established using Abaqus/Explicit 2016 for finite element computations.It is observed that the length dimension of cartridge is relatively small, which allows for the neglect of variations in the chamber pressure along different positions on the inner wall of cartridge.Therefore, assuming a uniform distribution of chamber pressure exerted on the inner wall of cartridge during the internal ballistics process is reasonable.The chamber pressure is calculated by classical internal ballistic theory[24],as shown in Fig.4.For single-shot firing,the internal ballistic time is extremely short, and therefore the effect of temperature changes on the strength of cartridge caused by thermal expansion can be neglected.

Fig.4.Chamber pressure calculated by classical internal ballistic theory.
After meshing, the finite element model was established as shown in Fig.5.The mesh adopted an eight-node reduced integration hexahedral element (C3D8R) with an average size of 0.2 mm, and the total number of nodes in mesh was 615,000.To verify the mesh independence,a finite element model with a total number of nodes of 1.134 million was compared, and the stress errors at the corresponding positions of chamber were within 2%,indicating that the mesh could ensure reliable calculation results.In order to save computational resources and improve efficiency, the finite element model with a mesh size of 615,000 nodes was selected for computation.To minimize the mutual interaction between components and the deformation effect of a beam-like structure at the bottom of cartridge, the analyzed area was set at the central position of cartridge.Furthermore,to mitigate potential errors, the simulation results were obtained by averaging the values of multiple nodes.
In the finite element model, the chamber material is medium carbon low alloy steel, the capping material is poly-ether-etherketone, and the cartridge material is carbon fiber reinforced composite.The mechanical properties of medium carbon low alloy steel and poly-ether-ether-ketone are described using the Johnson-Cook constitutive model [25,26].The general form is:
where, σ, ε, and ˙εrefrepresent stress, plastic strain, and reference strain rate,respectively.A,B,C,n,and m are material constants,and T* is the dimensionless temperature.(Temperature effects are not considered in this simulation model, so T* is taken as 0.)
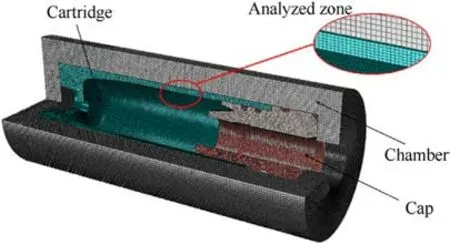
Fig.5.Finite element model after meshing.
The mechanical properties of carbon fiber reinforced composite materials are more significantly affected by strain rate in the fiber stacking direction, while carbon fibers exhibit strain rateindependent behavior.Therefore, for the carbon fiber composite cartridge, the focus is mainly on the correction of material properties in the radial direction.
Table 1 presents the specific parameters of the mechanical models for medium carbon low alloy steel and polyether ether ketone,as well as the quasi-static mechanical properties of carbon fiber composite materials.
The modulus correction form for carbon fiber reinforced composite materials can be expressed as [22]:
The Abaqus simulation software allows users to write subroutines to achieve more complex functionality.Among them, the VUMAT subroutine can edit the mechanical properties of materials,while the VDLOAD subroutine can provide a more accurate definition of the boundary conditions for applying loads [27].In this paper, the dynamic constitutive numerical model for carbon fiberreinforced composite materials is established using the VUMAT subroutine.Additionally, the VDLOAD subroutine is employed to define the loading region on the inner wall of cartridge due to chamber pressure during the interior ballistics phase more accurately.The calculation process of finite element simulation is shown in Fig.6.
4.Results analysis
4.1.Deformation process of cartridges
Taking the initial radial clearance δ = 0.08 mm, and cartridge inner radius r1=5.4 mm, outer radius r2= 6.4 mm as initial conditions,the radius changes of the inner and outer walls of cartridge obtained from the theoretical model and numerical simulation are shown in Fig.7.As the chamber pressure increases, the cartridge undergoes radial expansion deformation until the pressure reaches its peak, and then the cartridge rebounds as the pressure drops until it is completely unloaded.Comparing the deformation of the outer and inner radii of cartridge, the deformation of the outer radius is smaller than that of the inner radius, indicating that the cartridge wall thickness gradually decreases with the increase of chamber pressure, which is consistent with the actual situation.Comparing the deformation of cartridge under different loads, it can be seen that when the chamber pressure is below 295 MPa,the cartridge does not contact the chamber during the entire deformation process, and when the maximum chamber pressure of 375 MPa is applied, the outer wall of cartridge can contact the chamber.After touching chamber, the slope of the displacement curves for the inner and outer walls of cartridge, i.e., the deformation rate, significantly decreases.This is attributed to the significant constraint and support the chamber provides to the cartridge.
Combining the parameters provided in Refs.[16-18], Fig.8 presents the simulation results of the external wall deformations during the internal ballistics phase for brass and aluminum alloy cartridges under the same conditions.Compared to metal cartridges, carbon fiber-reinforced composite cartridges exhibit sufficient resilience after unloading,ensuring an adequate clearance for extraction.However,they only come into contact with the chamber at higher pressures.More consideration needs to be given to the behavior of the cartridge’s interaction with the chamber.
4.2.Effect of touching-chamber on the deformation and stress of cartridges
During the deformation process of the cartridge within the chamber, a tight fit between the cartridge and the chamber is generally advantageous.This is because once fitted, the cartridge will assist the chamber in bearing the internal pressure,promoting gas tightness and stability of the ammunition during firing.The radial clearance between the cartridge and the chamber is typically set at 0.04-0.08 mm.
In the investigation of the carbon fiber cartridge in this study,the initial clearances were adjusted to 0.04 mm and 0.06 mm.The deformation process of cartridge under a maximum chamber pressure of 295 MPa was calculated,as shown in Fig.9.The results indicate that when the initial clearances are 0.04 mm and 0.06 mm,the cartridge will come into close contact with the chamber bore at chamber pressures of 154 MPa and 230 MPa, respectively.At maximum chamber pressure, the maximum deformation of the outer wall of cartridge is 0.063 mm and 0.046 mm, respectively.This represents a reduction of 39.4% and 17.1% compared to the deformation of 0.076 mm when the cartridge is not in contact with the chamber (δ = 0.08 mm).For the inner wall of cartridge, the maximum deformations are 0.063 mm and 0.074 mm,respectively,representing a reduction of 25.5% and 11.7% compared to the deformations when not in contact with the chamber.
Fig.10 displays the circumferential and radial stresses on the inner and outer walls of cartridge for three radial clearances.When the initial clearance is 0.04 mm and 0.06 mm, the maximum circumferential stresses on the outer wall of cartridge are 850.3 MPa and 1215.6 MPa, respectively.These values represent reductions of 37.6% and 10.7% compared to the circumferential stress of 1362.2 MPa when the cartridge is not in contact with chamber (δ = 0.08 mm).As for the inner wall, the maximum circumferential stresses are 1354.9 MPa and 1638.0 MPa, respectively, which correspond to reductions of 25.6% and 10.0%compared to the stress of 1820.6 MPa when not in contact with chamber.Regarding radial stress,it can be observed that the radial stresses on the inner wall of cartridge for different radial clearances are close to the chamber pressure.This is due to the direct effect of chamber pressure on the inner wall of cartridge,which is consistent with Eqs.(14) and (16).From Fig.10(d), the radial stress on the outer wall of cartridge occurs after touching-chamber and is influenced by the contact pressure between the cartridge and chamber.As the radial clearance decreases, the outer wall of cartridge contacts the chamber earlier and experiences higher radial stress at maximum chamber pressure.
The above analysis indicates that the restricted behavior resulting from the contact and close fit between the cartridge andthe chamber significantly reduces the deformations of the inner and outer walls of cartridge and leads to a noticeable decrease in their corresponding circumferential stresses.The radial stresses on the inner and outer wall surfaces of cartridge are related to the chamber pressure and contact pressure,respectively.By comparing the deformations and stresses of cartridge for different radial clearance,it can be concluded that a close fit between the cartridge and the chamber is beneficial for its strength under the same chamber pressure.

Table 1 Material parameters of numerical simulation.

Fig.6.Calculation process of finite element simulation.
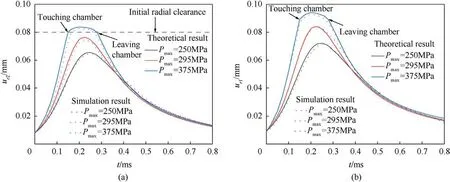
Fig.7.Radial deformation of the cartridge under different chamber pressure: (a) Outer wall surface; (b) Inner wall surface.

Fig.8.Radial deformation of different material cartridges (Pmax = 295 MPa).
Table 2 exhibits additional results obtained by theoretical and finite element models under various operational scenarios.The calculated error between the theoretical and simulation models does not exceed 5%, indicating a high degree of mutual validation between the two models.
4.3.Effect of cartridge wall thickness on the touching-chamber
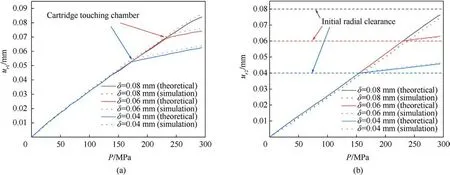
Fig.9.Deformation of the cartridge under different radial clearance (Pmax = 295 MPa): (a) Deformation of the inner surface; (b) Deformation of the outer surface.
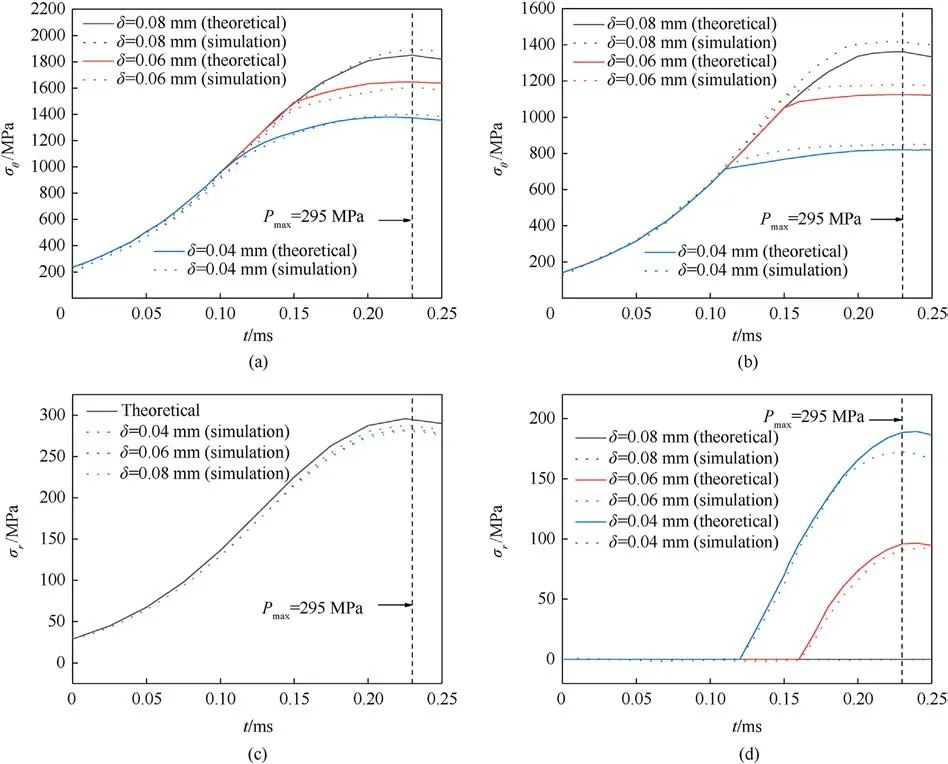
Fig.10.Stress of the cartridge under different radial clearance (Pmax = 295 MPa): (a) Circumferential stress of inner surface; (b) Circumferential stress of outer surface; (c) Radial stress of inner surface; (d) Radial stress of outer surface.
In the actual design of the matching between cartridge and chamber,the coherence of the movement of cartridge entering the chamber before shooting and exiting the chamber after shooting needs to be considered.This requires a necessary initial radial clearance between the cartridge and chamber.As analyzed in the previous section,it is advantageous for the strength of the cartridge to fit tightly to chamber.This section discusses the influence of the cartridge wall thickness on the fit between the cartridge and the chamber under constant radial clearance.
Maintaining a constant outer diameter r2of the cartridge, the inner diameter r1is adjusted to 5.5 mm, 5.6 mm, and 5.7 mm,resulting in corresponding cartridge wall thicknesses of 0.9 mm,0.8 mm, and 0.7 mm, respectively.The deformation of the cartridge’s outer wall surface, induced by the increase in chamber pressure and calculated using the theoretical model,is presented in Fig.11.Reducing the cartridge’s wall thickness leads to a tighter fit between the cartridge and chamber.As the wall thickness decreases,the chamber pressure required for the cartridge to contact the chamber decreases, resulting in increased radial deformation.This suggests that a thinner wall thickness corresponds to higher circumferential stress at maximum chamber pressure.Consequently,it becomes necessary to further analyze the thinning effect on the cartridge in conjunction with the material’s failure criteria.

Table 2 Errors between the results of theoretical model and finite element model (FEM).
Fig.12 presents the stress and strain nephogram of cartridge under various radial clearances.Combined with the analysis in subsection 4.2,it is evident that at the same instance,the stress and strain on the inner wall surface of cartridge is higher than that on the outer wall surface.This indicates that the inner surface of cartridge,serving as a critical region,is more susceptible to failure.
This paper adopts a failure criterion based on strain,focusing on the failure SFcaused by circumferential fiber tension and the failure SCcaused by radial matrix compression.The specific forms are represented as [28]:
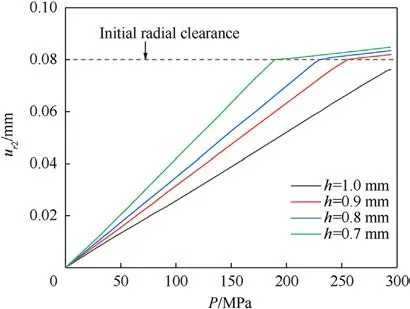
Fig.11.Deformation of the outer surface under different wall thickness(Pmax = 295 MPa).
When SFand SCare greater than 1, it indicates material failure.The failure criteria for the inner and outer surfaces of cartridges with different wall thicknesses at maximum chamber pressure are shown in Fig.13.The failure criteria for the outer surface of cartridge are higher than those for the inner surface,which means that the inner surface is more prone to failure than the outer surface.This is consistent with the nephogram results shown in Fig.12.Fig.14 illustrates the surface characteristics of cartridges with wall thickness of 1 mm and 0.8 mm after firing.The cartridge with a wall thickness of 0.8 mm exhibits crack failures on its surface, whereas the cartridge with a wall thickness of 1 mm appears relatively intact.This confirms that as the wall thickness decreases,the risk of failure in the cartridge increases.Combining the weight of cartridges with different wall thicknesses given in Table 3, it can be concluded that for carbon fiber reinforced composite cartridges,reducing the wall thickness can make the cartridge easier to touch the chamber and achieve weight reduction goals.However,thinner wall thicknesses will lead to a decrease in cartridge strength,making the cartridge more prone to failure.Therefore, more consideration needs to be given to the size design of the cartridge and chamber based on the corresponding failure criteria in practical engineering.
5.Conclusions
This study focuses on the continuous carbon fiber-reinforced composite cartridge and establishes a theoretical model and a finite element simulation model to describe the deformation of cartridge during firing.The general process of the cartridge deformation under different chamber pressure is determined, and the deformation and stress of cartridge under different chamber pressure, initial radial clearance, and wall thickness are analyzed.The theoretical analysis and simulation results show that.
(1) The computational results of the finite element model are consistent with the theoretical model, demonstrating the established theoretical model’s effectiveness in capturing the cartridge’s deformation process as it varies with chamber pressure.The maximum radial deformation of cartridge is positively correlated with the maximum chamber pressure.The cartridge will tightly touch chamber when the pressure is sufficiently high.Paying attention to the touchingchamber behavior of carbon fiber reinforced composite material cartridges is crucial.
(2) Under the same chamber pressure, the maximum radial deformation of cartridge decreases as the initial radial clearance decreases, and the corresponding circumferential stress decreases significantly.The touching-chamber behavior of cartridge can enable the cartridge and chamber to jointly withstand the chamber pressure, which is beneficial to ensure the launch strength of cartridge.
(3) The wall thickness of cartridge significantly affects its touching-chamber behavior.Thinner wall thickness results in lower chamber pressure for cartridge to contact chamber and larger maximum radial deformation.However,reducing the wall thickness of cartridge should be considered in conjunction with material failure criteria,as it can make the touching-chamber easier but also increase the risk of material failure.The cartridge size, radial clearance, and material characteristics should be comprehensively considered in engineering design.
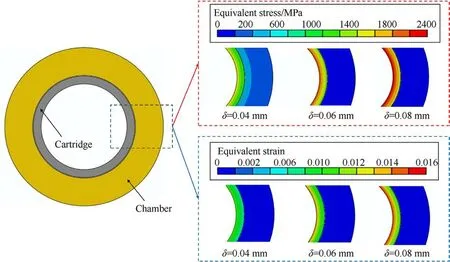
Fig.12.Nephogram of the cartridge under different radial clearance (Pmax = 295 MPa).
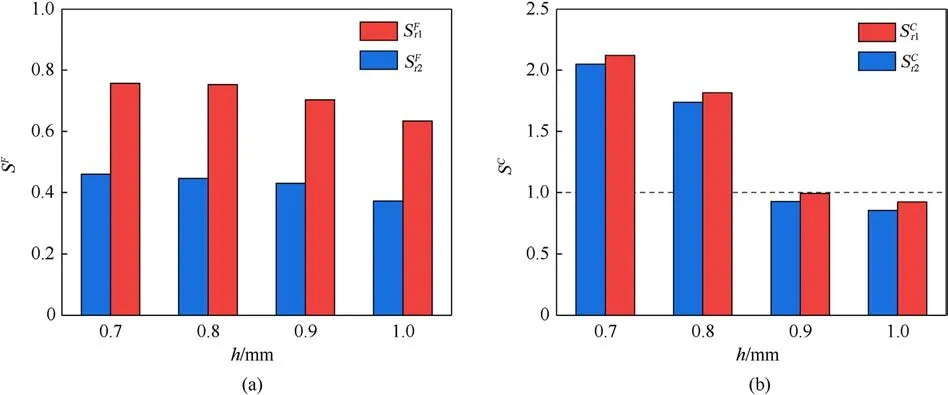
Fig.13.Failure criteria for cartridge with different wall thickness (Pmax = 295 MPa): (a) SF for circumferential fiber tension; (b) SC for radial matrix compression.

Fig.14.Experimental verification (a.Surface of cartridges after firing, b.Ballistic rifle for experiment, Pmax = 280 MPa).
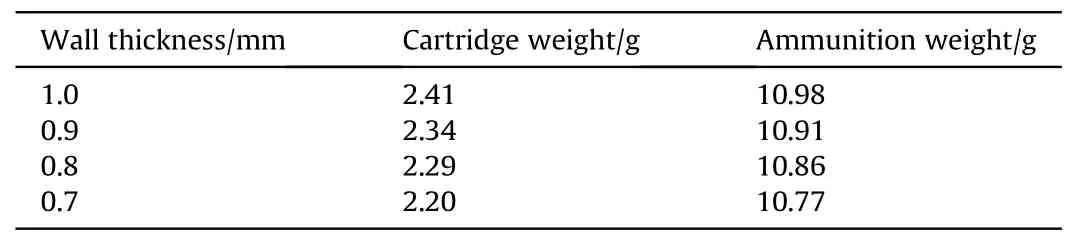
Table 3 Cartridge weight with different wall thickness.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors are grateful for the reviewers’ instructive suggestions and careful proofreading.This work was supported by the National Defense National Defense Pre-Research Foundation of China (Grant no.301030102).
- Defence Technology的其它文章
- Evolution of molecular structure of TATB under shock loading from transient Raman spectroscopic technique
- MTTSNet:Military time-sensitive targets stealth network via real-time mask generation
- Vulnerability assessment of UAV engine to laser based on improved shotline method
- Free-walking: Pedestrian inertial navigation based on dual footmounted IMU
- Investigation of hydroxyl-terminated polybutadiene propellant breaking characteristics and mechanism impacted by submerged cavitation water jet
- Estimation of surface geometry on combustion characteristics of AP/HTPB propellant under rapid depressurization

