Shock-induced energy localization and reaction growth considering chemical-inclusions effects for crystalline explosives

Ruqin Liu , Ynqing Wu ,*, Xinjie Wng , Fenglei Hung ,**, Xion Hung ,Yushi Wen

a State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing,100081, China

b School of Power and Mechanical Engineering, Wuhan University, Wuhan, 430072, Hubei, China

c Institute of Chemical Materials, China Academy of Engineering Physics (CAEP), Mianyang, 621999, Sichuan, China

Keywords:Shock responses Energy localization Crystalline explosives Chemical inclusions Reactive molecular dynamics

ABSTRACT Chemical inclusions significantly alter shock responses of crystalline explosives in macroscale gap experiments but their microscale dynamics origin remains unclear.Herein shock-induced energy localization, overall physical responses, and reactions in α-1,3,5-trinitro-1,3,5-triazinane (α-RDX) crystal entrained various chemical inclusions were investigated by the multi-scale shock technique implemented in the reactive molecular dynamics method.Results indicated that energy localization and shock reaction were affected by the intrinsic factors within chemical inclusions, i.e., phase states, chemical compositions,and concentrations.The atomic origin of chemical-inclusions effects on energy localization is dependent on the dynamics mechanism of interfacial molecules with free space volume, which includes homogeneous intermolecular compression,interfacial impact and shear,and void collapse and jet.As introducing various chemical inclusions,the initiation of those dynamics mechanisms triggers diverse decay rates of bulk RDX molecules and hereby impacts on growth speeds of final reactions.Adding chemical inclusions can reduce the effectiveness of the void during the shock impacting.Under the shockwave velocity of 9 km/s,the parent RDX decay rate in RDX entrained amorphous carbon decreases the most and is about one fourth of that in RDX with a vacuum void,and solid HMX and TATB inclusions are more reactive than amorphous carbon but less reactive than dry air or acetone inclusions.The lessdense shocking system denotes the greater increases in local temperature and stress, the faster energy liberation, and the earlier final reaction into equilibrium, revealing more pronounced responses to the present intense shockwave.The quantitative models associated with the relative system density (RDsys)were proposed for indicating energy-localization mechanisms and evaluating initiation safety in the shocked crystalline explosive.RDsys is defined by the density ratio of defective RDX to perfect crystal after dynamics relaxation and reveals the global density characteristic in shocked systems filled with chemical inclusions.When RDsys is below 0.9, local hydrodynamic jet initiated by void collapse dominates upon energy localization instead of interfacial impact.This study sheds light on novel insights for understanding the shock chemistry and physical-based atomic origin in crystalline explosives considering chemical-inclusions effects.

1.Introduction

Interpreting material responses to shock normally demands the multidisciplinary knowledge of materials science, condensed matter physics, and shockwave chemistry [1], particularly in the aspect of crystalline explosives.Crystalline explosives,which are of interest as the key energy source in modern explosive formulations,have caused an increasing concern due to their extensive applications in military and civil engineering.It’s believed that the physical responses and reaction kinetics of crystalline explosives are considered simultaneously to account for shock ignition and initiation [2-5].For shocking scenarios, shockwave stimuli drive crystalline explosives into an extreme state coupled with dynamic high pressure.Therefore, it can cause numerous noteworthy phenomena, involving elastic-to-plastic deformation [6-12], phase transition [13-18], ultrafast reaction [19-21], and inherent reaction evolution into deflagration or detonation [19,22-25], all of which have their roots in energy localization (known as hotspot)around some specified microstructures and defects.It’s emphasized that identifying shockwave-induced energy localization mechanism on microstructural heterogeneities[26-30]is a critical issue for promoting the state-of-the-art capabilities of the physicalbased prediction framework.This framework would be implemented to predict material plasticity and failure and evaluate shock responses and initiation safety in crystalline explosives.It’s also indicated that understanding the physics and chemistry of energy localization can aid in the science-based engineering and design of novel explosives[31].

Considerable endeavors have been focused on the atomic origin of energy-localization mechanisms in crystalline explosives.Those mechanisms comprise dislocations nucleation [7,8], nanoscale shear bands [9,11,32], internal cavity collapse and nano-jet[26,33-37], heterogeneous interface interaction [38-40], and grain-boundary frictional heating [41].Collectively, those studies ensure that predominant physics wouldn’t be omitted from the comprehensive description of crystalline material models in the safety predicting framework when invoked empirical parameters.Besides the above-mentioned mechanisms, by contrast with the host-guest inclusions incorporated into lattice via co-crystallization for desensitization [42,43], conventional chemical inclusions,including reaction by-products, carbon impurities, solvents, and gas inclusions [44-48], are unevenly deposited in crystalline explosives during the organic synthesis operation or crystallization procedure.In terms of carbon impurities, amorphous carbon and other carbon nanomaterials can also be the specified additives into explosive formulations for investigating detonation reactions.Consequently, those chemical inclusions seriously increase shock sensitivity in macroscale experiments, such as gap tests [49,50].However, implicit physical mechanisms cannot be unveiled adequately via current conventional shock experiments for chemical-inclusions effects in crystalline explosives.Fortunately,modern computer simulation has become an alternative pathway to usher the fundamental research on recognizing the physical mechanism behind material behaviors in shocked explosives.Recently, some simulating progress which mainly involves mesoscale and microscale models with physical-doping impurities has been promising in understanding the role of chemical inclusions in shock initiation.For instance, Rai et al.[51] performed the mesoscale modeling approach on the polymer bonded explosives(PBXs)and demonstrated that an expanded thermally expandable microsphere doped in PBXs perturbs the material flow, resulting in increasing shock sensitivity.Mi et al.[52] announced that the shock-to-detonation transition in nitromethane (NM) with airfilled cavities is faster than that in neat NM by the meso-resolved numerical simulations.Those mesoscale models can provide a quantitative understanding of shock responses within the twodimensional idealized geometry, but their sub-models involving material strength models and reaction chemistry models have still some uncertainties for physically realistic simulations of energy localization[29].As an atomic insight,reactive molecular dynamics simulation is also utilized for elucidating chemical-inclusions effects in crystalline explosives at the microscale level.Huang et al.[53] found that the local temperature response of a shocked defective β-1,3,5,7-tetranitro-1,3,5,7-tetrazoctane (β-HMX) crystal entrained slight oxygen is higher than that of HMX with amorphous carbon through reactive molecular dynamics simulations coupled with the multi-scale shock technique(MSST)[54].And it's also proved that owing to adiabatic gas compression,adding slight oxygen molecules into the void can even result in an initial local temperature increment compared to HMX samples containing a vacuum void.

Despite the existing effort in investigating chemical inclusions,chemical-inclusions effects are rarely considered for comprehending the microscale origin of shock-induced energy localization.More importantly, to date, some essential scientific questions remain:(i)what are the intrinsic factors of chemical inclusions that govern energy localization and determine shock responses,(ii)how will the shock-induced reaction path evolve, and (iii) what is the atomic origin of chemical-inclusions effects? Therefore, aiming to address the role of chemical inclusions in energy localization and initial reaction growth of α-1,3,5-trinitro-1,3,5-triazinane (α-RDX)and uncover the atomic origin of chemical-inclusions effects, we utilized the MSST method [54] implemented in molecular dynamics simulations based on ReaxFF-lg force field [22,55] to perform the shock simulations of α-RDX systems entrained various chemical inclusions.Details of models and simulating methods are described in Section 2.The energy localization behavior, chemical reaction analysis,system responses to shock loading,and chemicalinclusions microscale mechanism are presented in Section 3.Conclusions are depicted in Section 4.

2.Models and simulation details

2.1.Modelling systems construction

To investigate various chemical inclusions,consisting of reaction by-products, carbon, solvents, and gas inclusions, herein several defective α-RDX systems with a spherical void(abbreviated as VR)entrained amorphous carbon (CR), β-HMX crystal (HR), 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) crystal (TR), dry air (GR),and acetone molecules (AR) were considered in comparison to a perfect RDX crystal (PR).Those idealized models with physicaldoping inclusions are significant and available for a reasonable attempt to explore and understand chemical-inclusions effects in crystalline explosives.First, an initial orthorhombic unit cell of α-RDX with the lattice parameters of a =13.182 Å,b =11.574 Å,and c = 10.709 Å was obtained from the Cambridge Crystallographic Data Centre (CCDC) [56].A 6 × 7 × 7 RDX supercell whose three dimensions are 79.092 Å × 81.018 Å × 74.963 Å (shown in Fig.1),was constructed for PR containing 49,392 atoms.Based on the reported literature[53,57,58],the selected system size is available for both computing efficiency and cost in a scientific manner.For instance, homogeneous isothermal decomposition was simulated in the RDX system with 4536 atoms for 100 to 10 ns [57]; shock simulations were conducted in the HMX system with 29,568 atoms for 50 ps [53] and the 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) system with 15,552 atoms for several picoseconds [58], respectively.Thereafter, VR containing 40,656 atoms was built by removing an α-RDX-cluster sphere with a radius of 27 Å from PR and the mass center of removed RDX spherical-like crystal is in the mass central coordinate ((39.546,40.509, 37.4815) Å) of initial PR.Eventually, some approximate spherical molecular clusters with an average radius of about 20 Å were introduced at the mass center of VR for obtaining the RDX systems entrained different inclusions, respectively.Note that the mass centers of all molecules in doping molecular clusters are within the above-mentioned average radius.Those chemical inclusions comprise amorphous carbon (C5903) in CR, β-HMX (149 HMX molecules)in HR,TATB(174 TATB molecules)in TR,dry air in GR, and acetone (138 (CH3)2CO molecules) in AR.To improve the efficiency in the subsequent dynamics relaxation of CR, the initial structure of amorphous carbon was annealed from 3000 K to 300 K at different cooling rates in the multistage procedure and then equilibrated at 300 K for 15 ps in the canonical ensemble (NVT)with the Nosˊe-Hoover thermostat.A similar operating method was also reported by Odegard group [59,60].Radial distribution function g(r)of amorphous carbon was validated and shown in Fig.A1 of Appendix.The three-dimensional structures of all sphere-like chemical inclusions were shown in Fig.1.Specifically, dry air includes 610 nitrogen molecules,171 oxygen molecules,and 8 carbon dioxide molecules, whose gaseous molecular ratio is n(N2): n(O2):n(CO2)=77.3130%:21.6730%:1.0139%.This ratio is consistent with the shocked dry-air model in Ref.[61].

Fig.1.Three-dimensional structures of perfect α-RDX supercell and various sphere-like chemical inclusions, schematic diagram of shocking models, and their two-dimensional central sections with the thickness of 12 Å before and after dynamics relaxation.

2.2.Simulation details

All the simulations were conducted via the Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS, version 22Aug18) code [62] in conjunction with ReaxFF-lg force field[22,55], adopting the three-dimensional periodic boundary condition and the time step of 0.1 fs.ReaxFF-lg force field, possessing a London dispersion correction term,has been verified and then used extensively in the prediction and simulation of crystalline explosives involving RDX, HMX, PETN, and CL-20 [22,53,55,57,58].The MSST method, which enables to characterize the long-timescale evolution of shock-induced reactions in the periodic system within a suitable size, was utilized to simulate the perfect and defective RDX systems subjected to steady shock.In contrast to the non-equilibrium molecular dynamics (NEMD) explicit shocking method,the MSST method also can simulate multiple shock waves[63] and investigate shock responses of crystalline explosives in a periodic defective supercell [64,65].For reaching a given shock state, the MSST varies the cell volume and temperature in such a way as to fix the system to the shock Hugoniot and the Rayleigh line.These restraints conform to the macroscopic conservation laws dictated by a shock front.Therefore, it's noteworthy that energy localization and chemical reaction studied in this work are directly impacted by the system state of shocked materials governed via a given steady shockwave.And the charge equilibration(QEq)method with a convergence threshold of 1×10-6was used in the present study.Prior to shock loading, all RDX systems were minimized by the conjugate gradient algorithm with a force convergence threshold of 4.184×10-8kJ/(mol·Å).An ensemble of initial velocities using a random number generator with the specified seed was generated at 300 K based on the Maxwell-Boltzmann distribution for each RDX system.Then a dynamics equilibrium was performed by the Nosˊe-Hoover thermostat in the isothermalisobaric ensemble (NPT) at 300 K and 1.013 × 10-4GPa for 5 ps,adopting the temperature damping parameter of 20 fs and the pressure damping factor of 1000 fs with coupling all three diagonal components for hydrostatic pressure calculation.Particularly, to avoid the interfacial reaction between chemical-inclusions molecules and RDX during the dynamics relaxation process,a spherical bounding wall was defined for the chemical inclusions in GR and AR before giving an initial atomic velocity.The bounding wall would be unfixed after finishing dynamics relaxation.The above fixed-wall method was described in.Appendix A2 As shown in Fig.A2 of Appendix, it's indicated that each RDX system had reached the thermodynamic steady state after carrying out the specified relaxation operation.The resulting system densities after relaxation were 1.7942 g cm-3in PR,1.7354 g/cm3in CR,1.6440 g/cm3in HR,1.6475 g/cm3in TR,1.5742 g/cm3in GR,1.5211 g/cm3in AR, 1.4801 g/cm3in VR, respectively.And the relative volume changes of PR, CR, HR, TR, GR, AR, and VR were 0.5296%,-0.2173%,-0.3015%,-0.3446%,-0.5347%,-0.4491%,and 0.4376%, respectively.Ultimately, to investigate the effects of various chemical inclusions on shock responses, a steady-state shockwave velocity(Us)of 9 km/s was loaded into each RDX system along the x axis (i.e.the[100]orientation) for 50 ps,using the cell mass-like parameter of 200 g2/(mol2·Å4) and the reducing temperature factor of 0.01.The RDX models would be in the initial overdriven state in present shock simulations due to the loading shockwave speed being higher than the experimental RDX (the crystal density ρ = 1.767 g/cm3) detonation velocity of 8.639 km/s[66,67], and applying such overdriven shock to obtain initial reactions and material responses is reasonable and feasible for reducing computing resources consumption.Indeed, using the MSST method, it's noted that the shocked RDX system wouldn't remain in the overdriven state consistently but could evolve to the steady Chapman-Jouguet state with a long loading time.In addition,other steady-state shockwave velocities of 8 km/s and 10 km/s were also investigated in shock-reaction simulations for quantitative comparison and validation in subsection 3.4.During shock,the atomic dynamics trajectories and the molecular bonding information were outputted every 100 fs, respectively.After finishing all simulations, recognizing chemical fragments was implemented by the analysis algorithm based on bond orders reported in our previous work[67].Meanwhile,the physical field properties,including temperature and density, were calculated by the virtual grid technique.This technique was extensively adapted in the available Refs.[33-35,38,53].Furthermore, the visualization of atomic particles was rendered by OVITO [68].

3.Results and discussion

3.1.Formation and relaxation of energy localization

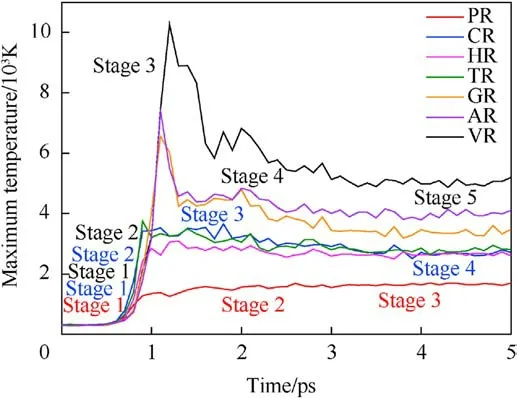
Fig.2.Maximum temperature curves (0-5 ps) during the initial shock loading(Us = 9 km/s).

To capture shock-induced energy localization, the maximum temperature history during the initial 5 ps(as shown in Fig.2)was recollected by meshing the RDX system into bins (12 Å×12 Å×12 Å)after subtracting out the center-of-mass velocity of atoms.And several temporal-spatial distribution maps of temperature were presented based on Cartesian geometry for all RDX systems.During the initial period of 5 ps, some two-dimensional temperature maps of cross-sections parallel to the x-y plane through the centroid of RDX systems were shown in Figs.3(a)-3(g)for comparison of local energy nucleation-to-growth and relaxation.In Fig.2 and Table 1,various stages were divided according to the changing speed of maximum temperature evolution with time.For energetic materials, this analysis strategy of maximum temperature has been used widely in the shocked molecular dynamics simulation [35,53,67,69] and the three-dimensional mesoscale modeling [70].During stage 1 (ending at 0.5 ps for all systems),maximum temperatures reach 337.57 K, 326.18 K, 331.44 K,298.32 K, 320.91 K, and 302.72 K in PR, HR, TR, GR, AR, and VR,respectively; owing to the interfacial impact and shear between amorphous carbon and crystalline RDX,the maximum temperature in CR ascends to 340.81 K,slightly higher than that in the remaining defective RDX systems[53].This phenomenon is inferred to be due to the high strength of spherical amorphous carbon.As shock loading continues, preliminary local high-temperature regions appear around the interface between bulk RDX molecules and void zone on account of shockwave-induced void compression.For RDX systems entrained solid inclusions, as interfacial vacancy almost vanishes, maximum temperatures in CR, HR, and TR reveal a moderate increment, growing to 3427.76 K, 2846.45 K, and 3749.87 K,respectively.Note that TATB is normally more insensitive than HMX.The fundamental reason for the higher local temperature observed in TR is inferred that shock compression generates substantial plastic deformation near the interface between bulk RDX and TATB molecules as a result of the rough surface of spherical TATB inclusion.By comparison, PR doesn't exhibit an obvious high-temperature localization event, whose maximum temperature reveals a lower amplitude,reaching 1565.77 K at 2 ps(stage 2) and later 1694.10 K at 5 ps (stage 3).Importantly, peak temperatures in GR,AR,and VR rise sharply,climbing to 6554.87 K,7392.00 K, and 10276.40 K, respectively.It's suggested that the dynamics collapse of a larger void results in more extensive plastic deformation of molecules around the void,triggering a remarkable increase in temperature.

Those local high-temperature phenomena (Figs.3(a)-3(g))coincide with the simulated distributions of local kinetic energy,as illustrated in Figs.4(a)-4(g).Snapshots of 12 Å thick slices of atoms colored by kinetic energy show that local kinetic energy also first occurs at interfacial atoms around the defect and then initial highconcentrated kinetic energy transfers to the remaining atoms as void almost disappearance,resulting in a serious temperature rise.Particularly,as illustrated in Fig.4(h),the resulting dynamic plots of atomic count versus atomic kinetic energy at 1.2 ps indicate that the dominant void collapse can lead to a higher increase in atomic kinetic energy in VR compared to remaining RDX systems.As shown in Fig.A3 of Appendix,the defect vanishing time of RDX entrained solid inclusions is shorter than 0.9 ps,while the void closure time of VR, AR, and GR almost exceeds 1 ps.Because of interfacial defect almost having vanished and successive heat transfer, maximum temperatures in CR,HR,and TR during stage 3(ending at 3 ps)show a slow decrease immediately,declining to 2909.17 K,2589.31 K,and 2803.07 K, respectively.

To further interpret the differences in temperature evolution,the dynamic plots of atomic count versus atomic temperature were shown in Fig.5 based on the quantitative analysis.It’s obvious that all distribution curves move to the high-temperature zone as shockwave energy loading, but the peak values of those curves in the defective RDX systems seem to show discrepancies with time.Hence it’s inferred that shock-induced energy localization and transfer are indeed associated with the phase states of chemical inclusions.Therefore, it’s also illustrated that both local-temperature morphologies and locations are significantly different under the local energy nucleation-to-growth procedure for the defective RDX systems as a result of entraining various chemical inclusions.Interestingly,an ellipse-like hot core occurs in VR at 1.2 ps as void disappears(Figs.3 and A3), while most irregular-shaped local temperature regions emerge in RDX with inclusions because of complex interfacial interactions (including adiabatic compression) between chemical inclusions and RDX.Those interactions are related to the relative compressibility of chemical inclusions against RDX.A hightemperature region at 2 ps locates around the perpendicular bisector of x axis for HR and TR and concentrates on the nucleus center of cross-sections for GR,AR,and VR,while high-temperature regions of CR spread over the edge of inclusion.In addition, all hot cores in CR,GR,AR,and VR decay in size after 2 ps,while hot cores in HR and TR are strengthened on temperature distribution, which is ascribed to the energetic inclusions (HMX and TATB) releasing energy via self-decomposition.It’s implied that the pathway of energy-localization relaxation is also determined by the compositions of inclusions.Thereafter, during stage 4, maximum temperatures in GR,AR, and VR begin to fall quickly due to heat dissipation and transmission,retaining 3441.56 K,4007.60 K,and 5128.77 K at 3 ps, respectively, while maximum temperatures in CR, HR, and TR relax to 2739.11 K, 2603.98 K, and 2810.12 K at 5 ps, respectively.During stage 5,maximum temperatures in GR,AR,and VR ultimately relax to 3477.43 K, 4105.01 K, and 5190.74 K at 5 ps, respectively.Therefore,it’s suggested that the introduction of chemical inclusions can effectively damp the degree of maximum temperature rise originating from molecules’ collision around defects during the shock-induced void collapse process.It’s further confirmed that the degree of shock response in defective RDX systems can be reduced by the introduced chemical inclusions with reasonable concentrations into VR compared to adding the slight oxygen in the previous study[53].

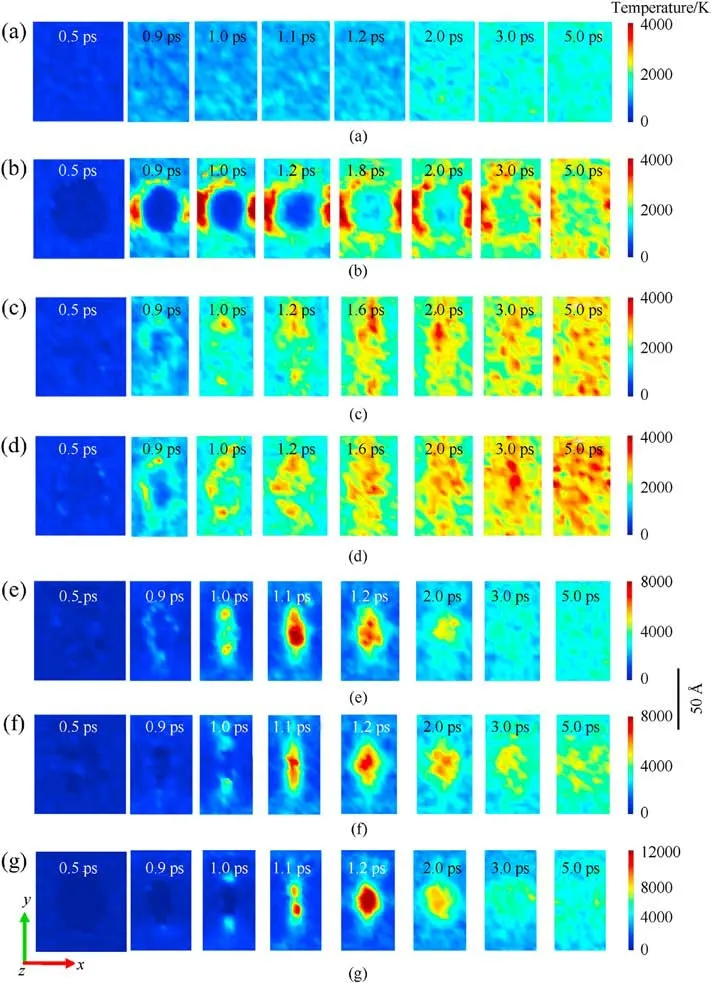
Fig.3.Temperature distribution of RDX systems with different color scales: (a) PR, (b) CR, (c) HR, (d) TR, (e) GR, (f) AR, and (g) VR in the case of Us = 9 km/s.

Table 1 Comparison of extremum temperatures(T)during various stages(Us = 9 km/s).

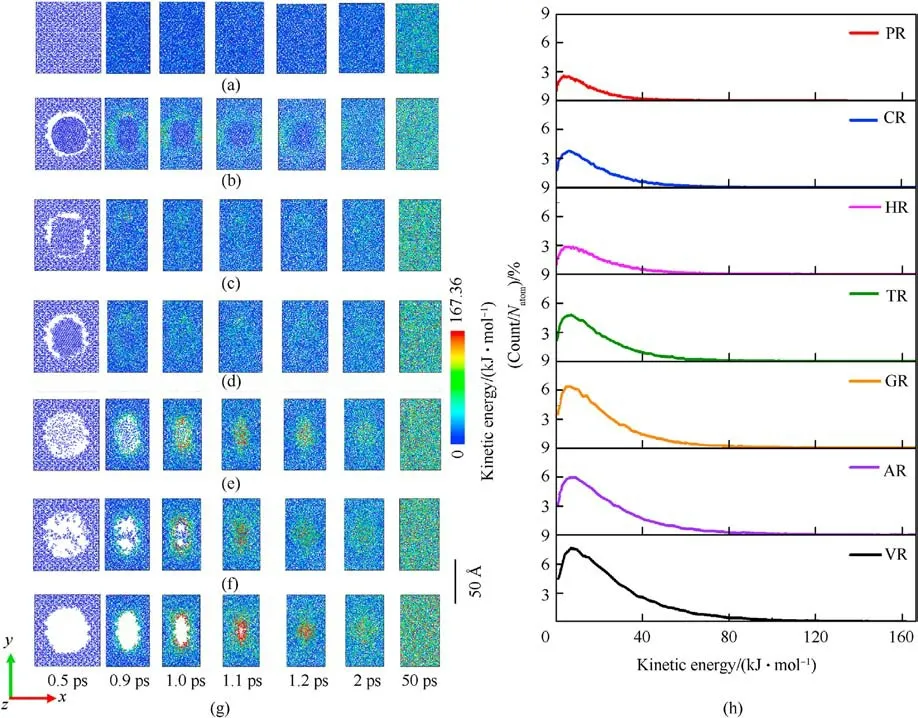
Fig.4.(a)-(g)Snapshots of kinetic energy slices with a thickness of 12 Å through the center of mass:(a)PR;(b)CR;(c)HR;(d)TR;(e)G;(f)AR;(g)VR;(h)Plots of scale normalized atomic count versus atomic kinetic energy at 1.2 ps.Natom is the total number of atoms in each RDX system.

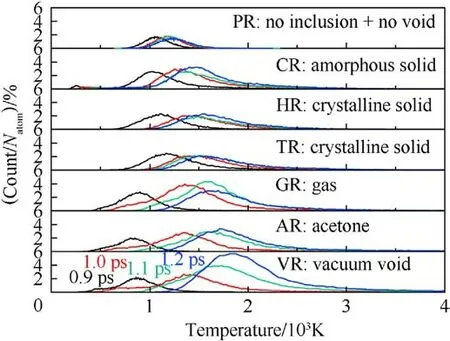
Fig.5.Plots of scale normalized atomic count versus atomic temperature(0.93-1.2 ps)in the case of Us = 9 km/s.

To summarize, it’s believed that energy-localization nucleation site,growth morphology,and even relaxation pathway after defect closure are indeed associated with compositions and phase states of chemical inclusions for shockwave-induced energy localization process; more specifically, the resulting maximum temperature of VR(containing a vacuum void)increases highest,followed by those of the RDX systems entrained gas/acetone inclusions, and then those of the RDX systems entrained solid inclusions.

3.2.Shock-induced decompositions and chemical species analysis

Shockwave can first bring a compression role in crystalline molecules, whose centroid distance decreases, then cause plastic deformation and cleavage of trigger bonds, such as N-N in nitroamino group, and final result in reaction growth, even leading to high-violent explosion or detonation when suffered intense shock.Fig.6(a) and Figs.7-9 display the evolution history of RDX and some key reaction species in each RDX system under the initial overdriven shocking.It’s indicated that the acceleration of initial decomposition reactions is initiated by high-temperature localization in all defective RDX systems.Considering the half-time decay as a benchmark, it’s evident that the half-time period of RDX in RDX systems entrained solid inclusions is longer than those of the remaining RDX systems entrained gas/acetone inclusions,due to the compressibility of gas/acetone molecules being higher than that of solid molecules under the same condition.Concerning solid inclusions,their effects on the half-time period of RDX show a phenomenal divergence, i.e., a reduction tendency from CR to HR,and TR.Hence one can conclude that the decomposition progress of RDX is determined by the phase states and compositions of chemical inclusions under the same overdriven loading condition.Hence the raw RDX molecules of PR were completely consumed at 34.2 ps(Fig.6(a)), showing the slowest shockwave-induced decay.Nevertheless,the thorough decomposition of RDX in CR,HR,TR,GR,AR, and VR occurs at 11.6 ps,8.5 ps, 8.2 ps,6.1 ps,5 ps,and 3.5 ps,respectively.

For quantitative comparison, the first-order decay exponential equation [71,72] was adopted and listed as follows:

where nRDX（t） is the molecular number of RDX at t; kRDXis the decay rate(ps-1);t is the loading time(ps);tindis the induce time(ps) for RDX decomposition.

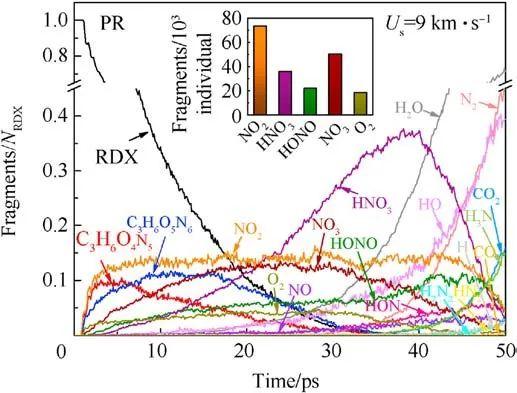
Fig.7.Scale normalized evolution of vital fragments in PR under the shockwave velocity of 9 km/s.Column inset indicates the cumulating amounts of interested intermediates including NO2, HNO3, HONO, NO3, and O2 before 25 ps.

The fitted decay rates of seven RDX systems were described in Table 2,and R2is the adjusted R-squared,denoting the coefficient of determination in the nonlinear fitting.Results show that chemical inclusions play a negative role in the RDX decomposition process compared to VR.It’s illustrated that adding chemical inclusions can reduce the effectiveness of the void during the shock impacting.The parent RDX decay rate in CR decreases the most and is about one fourth of that in VR under the shockwave velocity of 9 km/s.In terms of resulting RDX decay rate,it’s indicated that solid HMX and TATB inclusions are more reactive than carbon impurity but less reactive than dry air or acetone inclusions.Note that the faster decay rate of reactant denotes more sensitive to shock.With RDX substrate decomposing, as shown in Fig.6(b), the accumulative number of all products increases slowly for PR in 50 ps,while it first increases and then tends to a dynamics balance for the defective RDX systems.Since HMX, TATB, and acetone underwent decomposition,their decay rates were also fitted by Eq.(1).Results show kHMX= 4.290 ± 0.078 ps-1(tind= 0.8 ps, R2= 0.9514),kTATB= 4.137 ± 0.117 ps-1(tind= 0.7 ps, R2= 0.9018), and kAcetone=3.252±0.068 ps-1(tind=0.9 ps,R2=0.9370).Note that kHMXis higher than kTATB.It’s indicated that the entrained HMX crystal is more sensitive to the present overdriven shock than the TATB crystal.Fig.6(b)implies that HR is the highest concentration of total products at 50 ps due to HMX molecules decomposing rapidly, while VR, TR, and AR have a similar concentration of total products, being higher than GR and following CR.Compared with PR, as illustrated in Figs.7 and 8, nitrogenous intermediates (NO2,HNO3, HONO, and NO3) and oxygen generate quickly and then vanish rapidly before 25 ps in defective RDX systems,where initial dissociation derives from N-N and N-O bonds in nitroamino group(shown in Figs.A4 and A5 of Appendix).Figs.8 and 9 demonstrate that the life and concentration of those intermediates are altered by chemical inclusions.The longer life of key intermediates results in a higher cumulative concentration but a lower peak concentration.On the other hand, as the stable gaseous products (H2O, CO2, and N2) are released every time step, transient amounts of OH and H fragments in all defective RDX systems increase gradually after going through the first peak of concentration.But, by comparison,their increasing cumulative concentrations and amounts show a remarkable increase from CR to VR(as shown in Figs.9(a)-9(f))due to chemical-inclusions effects.For RDX systems entrained gas/acetone inclusions, it’s obvious that the increasing number of HO and H would result in the decreasing number of H2O after 30 ps.This phenomenon can be attributed to the fact that chemical inclusions in crystalline explosives affect shock reaction kinetics and thereby change the cumulative history of decomposition products with time.Therefore, the earlier intermediates are consumed, the faster final products reach a stable concentration (Fig.9).It’s suggested that the final reaction pathway towards violent deflagration or detonation is directly regulated and accomplished via hightemperature localization events stemming from chemicalinclusions effects.

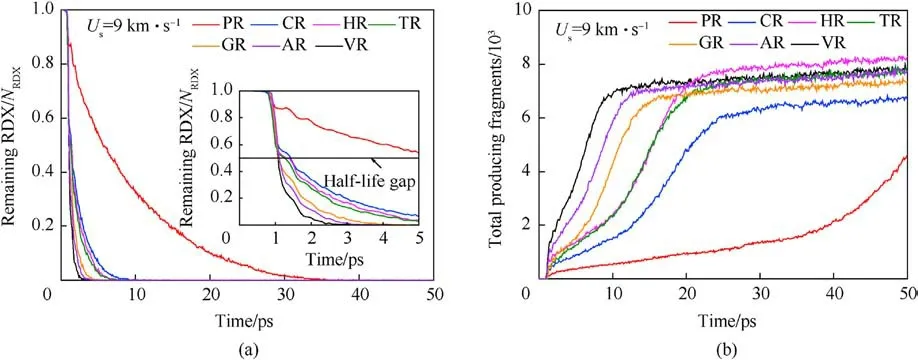
Fig.6.(a) Scale normalized evolution of remaining RDX (0-50 ps).NRDX represents the number of raw RDX molecules in each system; (b) Comparison of the total number of products under the shockwave velocity of 9 km/s.

Table 2 Reaction kinetics of RDX under the shockwave velocity of 9 km/s.

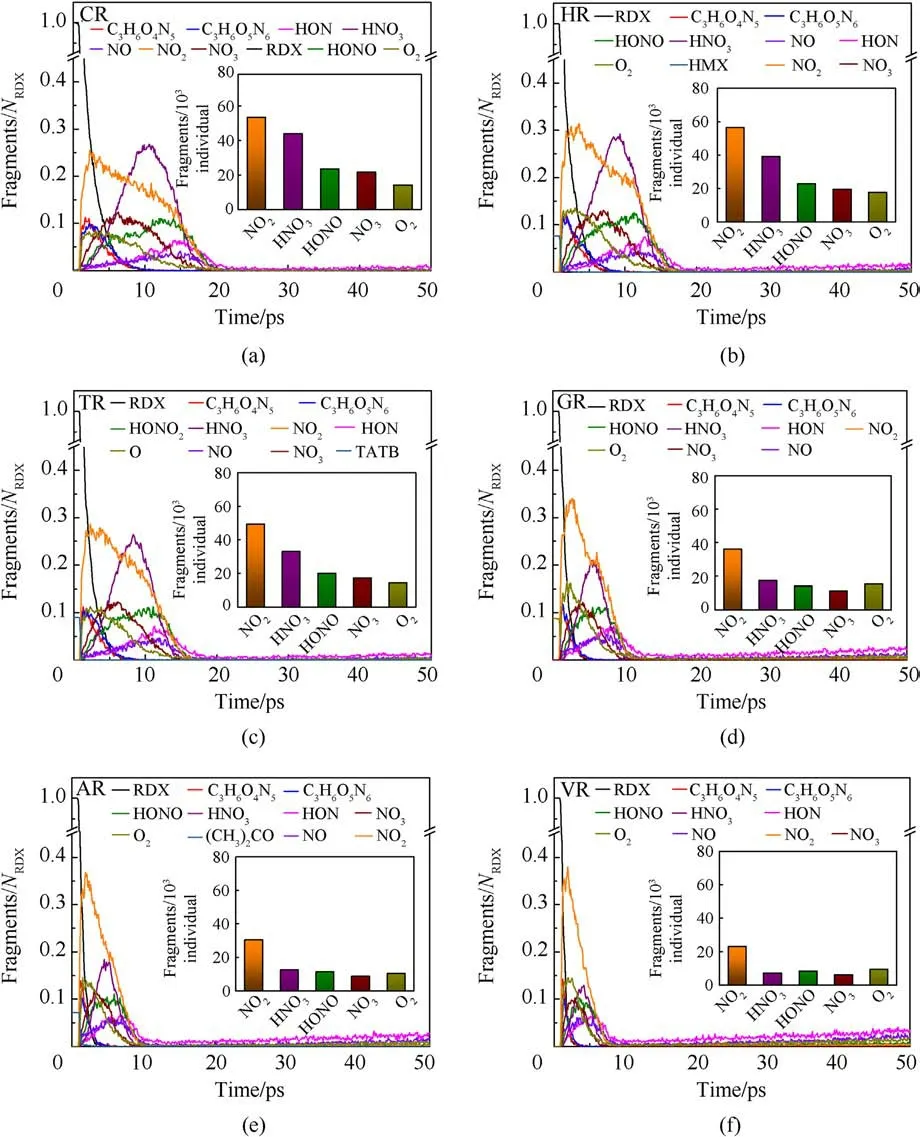
Fig.8.(a)-(f)Scale normalized evolution of raw reactants and intermediates in defective RDX systems under the shockwave velocity of 9 km/s.Column insets(a)-(f)indicate the cumulating amounts of interested intermediates including NO2, HNO3, HONO, NO3, and O2 before 25 ps.

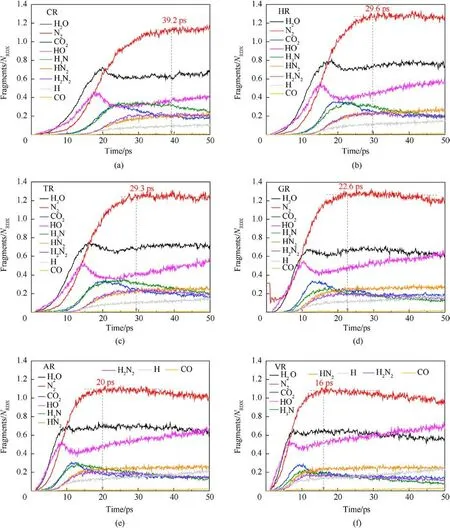
Fig.9.Scale normalized evolution of some secondary products and stable final products in (a) CR, (b) HR, (c) TR, (d) GR, (e) AR, (f) VR under the shockwave velocity of 9 km/s.

3.3.Global system responses under the shockwave loading

Fig.10(a) indicates a significant difference in the average temperature history due to chemical inclusions.The order of average temperature growth over the first 5 ps is VR ＞AR ＞GR ＞TR ＞HR ＞CR ＞PR,which is entirely consistent with the rank of plotted RDX decay rate.The average temperature in each defective RDX system is higher than that in perfect RDX with steady shockwave loading, indicating an enhancing role of crystal defect on fast heat release transformed from shock-compression plastic work and chemical energy.As a result, average temperatures of VR,AR,GR,TR,HR,CR,and PR rise to 6422.80 K,5858.95 K,5528.88 K,4844.47 K,4942.84 K,4391.34 K,and 3192.56 K at 50 ps,respectively.For those defective RDX systems, the evolution tendency of average temperature consists of three stages, i.e., (i) the period of a dramatic increase in temperature due to the occurrence of local high-temperature zone before 1.2 ps, (ii) the transition period due to the initiation of intermediate chemical reaction,and(iii) the period of a slow increase in temperature at the approximately constant rate for continuously generating final explosion products.HR can produce more nitrogenous intermediates than TR in the early stage(seen in Figs.8(b)and 8(c)),leading to the higher average temperature.The larger amounts of those intermediates can delay the parent RDX decomposition.Therefore,the RDX decay rate in HR is lower than that in TR.When RDX decomposes completely, average temperature increases slowly.The higher concentrations of products (including intermediates) is conducive to reaching the state of final reaction earlier.Note that the average temperature of HR is higher than that of TR after the transition period(～16.6 ps).Despite the surface roughness of solid inclusions,it’s indicated that the degree of shock responses in high-energetic crystalline inclusions (HMX and TATB) determines subsequent temperature response driven by violent final reaction for a given composite energetic system.Referred to the temperature spike measured in the nanosecond shock experiment [73], VR, AR, and GR, with or without gas/acetone inclusions, can still accomplish a dynamics transition to final reaction early,forming a higher level of overall temperature.

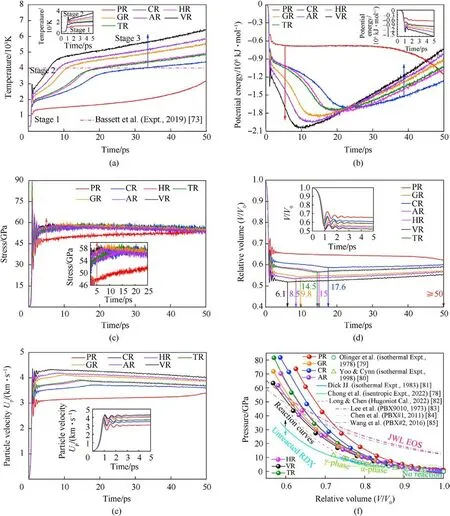
Fig.10.Evolution of overall responses(Us=9 km/s)including:(a)Average temperature;(b)Shift normalized potential energy;(c)Stress;(d)Relative volume;(e)Particle velocity with time.(f) Relation between pressure (P) and relative volume (v = V/V0) of shocked RDX before 1 ps.

The change of potential energy is associated with the exothermic reaction,which describes the overall rate and degree of thermal decomposition of energetic materials.For comparison,the shift normalized potential energy in shocked RDX systems was plotted in Fig.10(b).With the initial high-rate decomposition of RDX before 1 ps, a conspicuous decrease in the shift normalized potential energy is observed, descending potential energy by 1.1417 × 106kJ/mol in VR, 1.0351 × 106kJ/mol in AR,9.9643 × 105kJ/mol in GR, 7.8811 × 105kJ/mol in TR,7.6841 × 105kJ/mol in HR, 7.6840 × 105kJ/mol in CR, and 4.9991×105kJ/mol in PR,respectively.Thereafter,potential energy keeps dropping with decomposition reaction and following increases with shockwave loading in defective RDX systems,while it starts to diminish prominently in PR behind a moderate equilibration of 20 ps.Those phenomena are consistent with the shocked β-HMX simulations[53],which implies that the declining tendency of shift normalized potential energy is dependent on the decomposition rate of reaction substrates.Generally, chemical inclusion boosts the degree of energy liberation compared to PR, further confirming a sensitization influence of chemical inclusions or impurities upon crystalline explosives.On the other hand,toward the crystal defect engineering of energetic materials,the energy release rate of defective RDX systems can be tuned by introducing chemical inclusions, whose role is dependent upon the intrinsic factors of chemical inclusions,involving phase states,chemical compositions,and concentrations.Significantly,during the energy releasing stage,the rate of energy release in RDX systems entrained gas/acetone inclusions is higher than that in RDX systems entrained solid inclusions, and the degree of energy liberation in RDX systems entrained energetic-crystalline inclusions(i.e.,HR and TR)is larger than that in CR.

Figs.10(c)and 10(d)present the evolution of system stress and relative volume in RDX systems subjected to the steady shockwave of 9 km/s.After the initial fluctuation, internal stress in defective RDX systems rises to approximately 58 GPa(Fig.10(c)),then tends to a brief equilibrium, and eventually reduces slightly as volume expansion [74], whereas it has slow but steady growth for more than 40 ps in PR, denoting PR requiring a long time for RDX complete decomposition.Faster stress increase implies more pronounced responses to shock [71].Hence, under the shockwave velocity of 9 km/s, VR has a higher degree of shock response than RDX systems entrained gas/acetone inclusions, followed by RDX systems entrained energetic-materials inclusions, and then CR,which agrees with the evolution trend of temperature.Consequently, it’s illuminated that adding chemical inclusions into a vacuum void can modulate the degree of shock response of porous energetic material, and note that the eventual degree of altering shock response is intimately related to chemical inclusions.

After two successive decreases at diverse rates, as marked in Fig.10(d), volume swells at the characteristic time after declining.The rank of shrink volume is tied to the initial density[71],whose magnitude is determined by the filled concentration of chemical inclusions in a given volume.The denser RDX system(i.e.,reducing porosity) denotes the slower increases in temperature and stress.Fig.10(e)demonstrates that a higher particle velocity is required in the lower density system (i.e., more porous RDX) for imposing a steady shockwave propagating over the bulk RDX.In this case,with a given shockwave speed, it's deduced that such a less dense RDX system could have a shorter run to detonation[75,76],indicating a higher degree of shock response to the shockwave of 9 km/s.The above potential behavior can be preliminarily confirmed from the critical time of releasing final products steadily(Figs.9(a)-9(f)).As expected, Fig.10(f) shows that pressure response decreases at a given relative volume as reducing initial density,agreeing with the Rankine-Hugoniot relation of P = ρ0UsUp[77] and revealing a higher degree of compressibility.When relative volume outnumbers 0.92, no obvious reaction occurs in most RDX systems,whose P-v curves almost overlap with the experimental isentrope[78], hydrostatic isotherm [79-81], and calculated Hugoniot line[82].In comparison, with the decreasing relative volume, the denser RDX system outruns the Jones-Wilkins-Lee equation of state(JWL EOS) curves of detonation products [83-85] earlier and consequently reaches the overdriven state faster.

Therefore, it’s indicated that RDX entrained the lower concentration inclusions shows a higher degree of shock response with the increasing compressibility [86].By considering the shock-induced response mechanism corresponding to chemical inclusions, it’s also proved that a less-dense RDX system is easier to reach the steady detonation state when impacted by the shockwave velocity of 9 km/s.Hence such a less-dense RDX system can accomplish a faster degree of energy liberation and a higher increase in overall temperature.

3.4.Chemical-inclusions effects on shock responses and their atomic origin

In the perspective of molecular crystal, defect supplies free volume space in lattice[71,87],reduces bulk density,and serves as hotspots under shock stimuli.For the defective RDX, the free volume space of atoms at defects determines the response to a shockwave.Hence chemical-inclusions effects on energy localization could be understood from an insight of free space volume.To further confirm the relationship between free space volume and energy localization, as shown in Figs.11-13, we have investigated the spatial distribution and amount of high-temperature particles during the initial period of local temperature formation, the evolution of local high-temperature bins’ number with time, and the subsequent dynamics position of atoms in an interfacial RDX molecule beside void along x axis for a given periodic cell,respectively.Fig.11 reveals that the energy-localization event first appears in the interface between RDX molecules and chemical inclusions, and then the spatial locations and morphologies of hot zones present diversification and variation, due to chemicalinclusions effects.For instance, RDX systems entrained solid inclusions have an uneven spatial distribution of local hightemperature zone, while VR, AR, and GR have high-concentration hot cores converged at the system center.The degree of RDX decomposition increases with the improving high-temperature atomic count (Fig.11).Similarly, as illustrated in Fig.12(a), the faster increase in local high-temperature bins count represents the hotter energy-localization event for the overall shocking procedure.As shown in Fig.12(b), the critical time of defective RDX systems where all bins exceed 2000 K is significantly shorter than that of PR on account of defective RDX systems having a larger free space volume.Meanwhile, the free space volume of defective RDX systems is also affected by the entrained chemical-inclusions concentrations, resulting in diverse temperature maps at the critical time via different dynamics dominant mechanisms.Combined with Fig.6(a), it’s also indicated that the hotter and stronger energy-localization response favors the more rapid decomposition of RDX due to chemical-inclusions effects.In brief, the lower concentration of chemical inclusions filled into a vacuum void denotes the smaller system density, which suggests interfacial molecules beside defects possess the larger free space volume.Such a less dense RDX shows a higher local-temperature response,facilitating the initial shock-induced decomposition of reaction substrates.

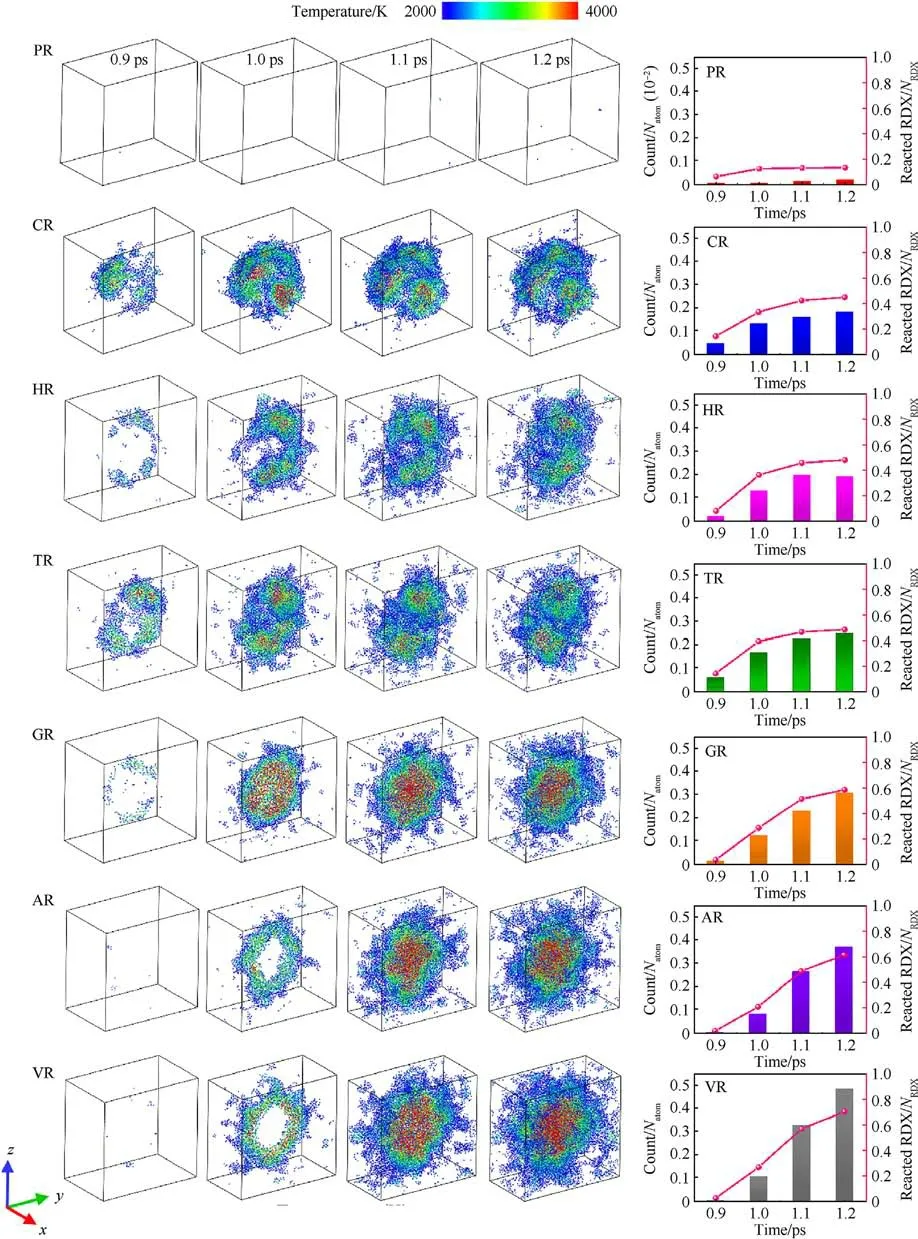
Fig.11.Snapshots of hot-zone atoms with the temperature exceeding 2000 K, and their scale normalized atomic count and consumed RDX molecules (0.9-1.2 ps) in the case of Us = 9 km/s.

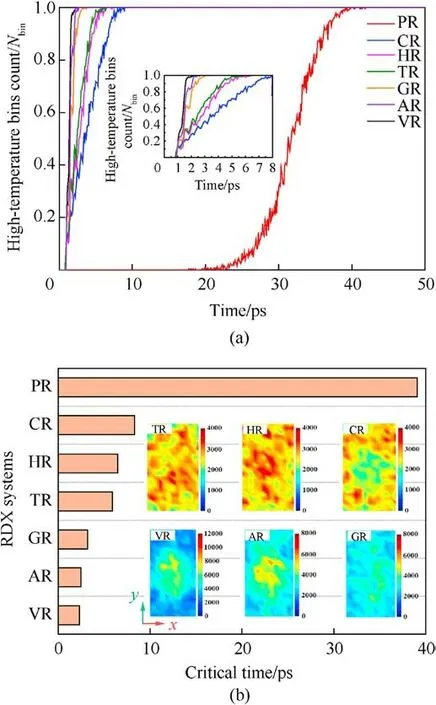
Fig.12.(a)Scale normalized evolution of local high-temperature bins(exceeding 2000 K) count under the shockwave velocity of 9 km/s.Nbin is the total number of bins; (b)Comparison of the critical time for all bins reaching above 2000 K.Insets indicate the temperature distribution of defective RDX systems at the critical time with different color scales.

For VR,AR,and GR,interfacial RDX molecule(RDX#1,as marked in Fig.13)would become the expanding/jetting material and move farther away from RDX#2 with the increasing of free space, suggesting void collapse accessing into hydrodynamic regime [33].Note that the displacement distance of RDX#1 in AR is greater than that in GR at 1.2 ps, demonstrating the inclusions’ concentration being an essential contributor to chemical-inclusions effects except phase state and chemical composition.Meanwhile,RDX#1 reacted earlier prior to RDX#2,which indicates that chemical reaction first occurs in moving interfacial molecules instead of bulk molecules when subjected to the intense shock for RDX with vacuum void or gas/acetone inclusions [88].Among RDX systems entrained solid inclusions, RDX#1 shifts slightly along the shock direction as interfacial impacting of inclusions for HR and TR, whereas RDX#1 and its surrounding RDX molecules are squeezed and sheared by amorphous carbon sphere and travel to the shrinking boundary for CR.RDX#1 in PR maintains the same displacement as RDX#2 due to homogeneous intermolecular compression within a given free space.As sketched in Fig.14(a), the above dynamics mechanisms denote the diverse levels of energy localization capacity in crystalline explosives with various entrained chemical inclusions.The plots of atomic count versus atomic displacement magnitude at 1.2 ps were illustrated in Fig.14(b).It’s further elucidated that the larger free space of interfacial molecules leads to their farther maximum displacement, triggering the more violent energylocalization behavior.Consequently, the atomic origin of chemical-inclusions effects on energy localization is dependent upon the dynamics mechanism of interfacial molecules with free space volume.

Furthermore, some scale normalized filling factors, including relative atomic filling degree (RFatom), relative filling density of chemical inclusions (RFDci) inside a void, and relative system density (RDsys) (as defined in Appendix A5), were applied for quantitative evaluation of chemical inclusions.As shown in Fig.A6 of Appendix, it’s proved that the lesser RFatomdenotes the lower RFDciand RDsys, indicating greater increases in local and overall temperatures due to dynamics mechanism transformation.RDsysreveals the global density characteristic in RDX because of filling inclusions, hence it’s employed for developing some interesting physical models considering chemical-inclusions effects.Therefore,RDsys-dependent critical-time (tc), energy-localization, and decomposition rate (k) models were built by the following exponential equation:

where ΔTmis the maximum temperature increment due to energy localization; a0, b0, a1, b1, a2, and b2are constants for a given shockwave velocity.Those expressions can be integrated as the function (f), i.e., f = f(RDsys).

As plotted in Fig.15, those proposed models are in good correlation with RDsys.For the defective RDX, Fig.15(a) shows that introducing low-concentration inclusions reduces the critical reaction time and thus facilitates final reactions.In Fig.15(b),Eqs.(3)and (4) were also verified and compared by the reference data of shocked HMX[53].To further validate the above models and then promote their application in general intense-shock scenarios for the future,various shockwave velocities(Us=8 km/s and 10 km/s)were adopted for shocking RDX simulations.The results consisting of temperature evolution and RDX decomposition were shown in Fig.A7 of Appendix.And Fig.15(c) illustrates the validation of proposed models concerning RDsysat different shockwave velocities, which indicates those models’ application in such intenseshock conditions.Shockwave velocity direct affects material shock responses.It’s would be an interesting attempt that Eqs.(3)and(4)are extended for an implication of the general formulation concerning shockwave velocity, i.e., f = f(RDsys, Us).However, the key concern in this work is to identify predominant microscale mechanisms and chemical reactions originating from chemicalinclusions effects instead of focusing on the model extension from the massive data based on molecular dynamics calculations.More importantly, in the case of Us= 9 km/s, the plotting results show kRDX= 0.3861(RDsys)-9.1719(R2= 0.9359) and ΔTm= 1287.0239(RDsys)-10.4648(R2= 0.9584) for RDX;kHMX= 0.0699(RDsys)-18.5572(R2= 0.9929) and ΔTm=1189.0501(RDsys)-13.6493(R2=0.9908)for HMX.When RDsysis below 0.9, decomposition rate exceeds 1 ps-1and local temperature increases by 4000 K for RDX entrained chemical inclusions in the present study of Us= 9 km/s, which indicates that energylocalization mechanism is transformed from defect interfacial impacting to local hydrodynamic jet initiated by void collapse.Similarly, decay rate transcends 0.5 ps-1and local temperature ascends by 5000 K for the reported β-HMX system[53].

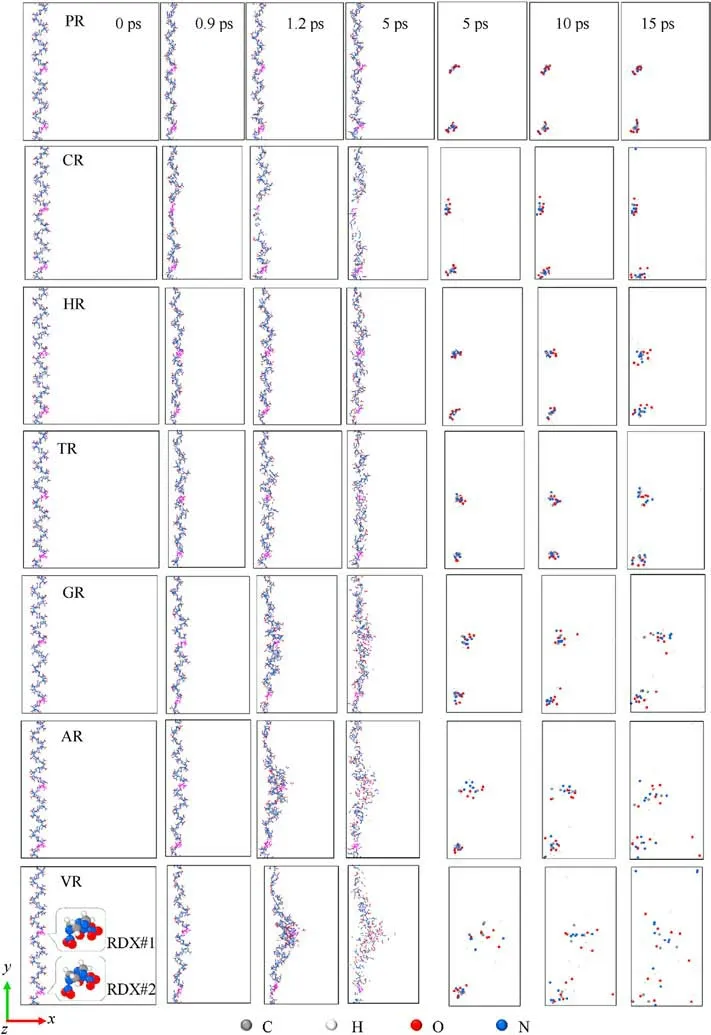
Fig.13.Snapshots of 12 Å thick RDX-layer slices(0-5 ps)and atoms of two given RDX molecules(5-15 ps)(Us=9 km/s).RDX#1 and RDX#2(magenta-colored conformation)are located at the interface of void and in the bulk crystal,respectively.Particle identifiers are 20245-20265 and 18,166-18186 in the defective RDX, whereas they are 24,277-24297 and 21,253-21273 in PR.

4.Conclusions

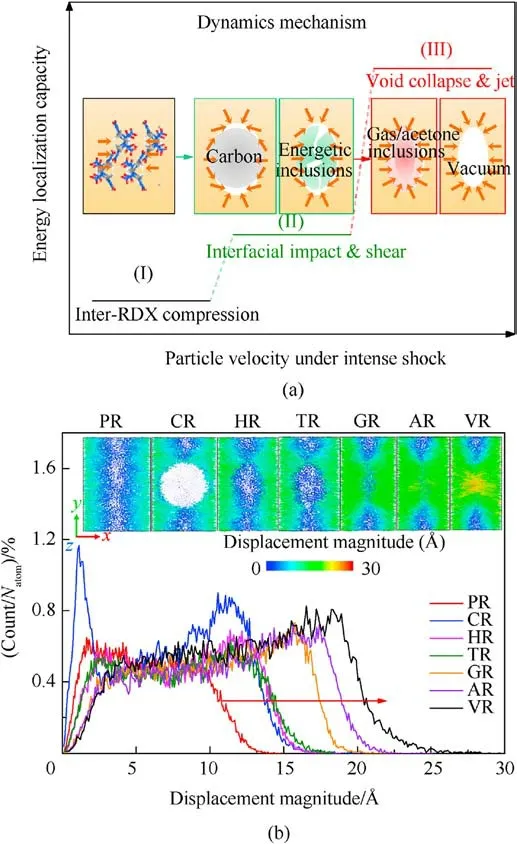
Fig.14.(a) Dynamics mechanism predominating energy-localization capacity; (b)Plots of scale normalized atomic count versus atomic displacement magnitude at 1.2 ps(Us = 9 km/s).Insets show the distribution snapshots of displacement magnitude of 12 Å thick cross-sections parallel to the x-y plane.

In conclusion,reactive molecular dynamics simulations uncover that the atomic origin of chemical-inclusions effects on energy localization is determined by the dynamics mechanism of interfacial molecules with free space volume.Those mechanisms comprise homogeneous intermolecular compression, interfacial impact and shear, and void collapse and jet, which are dependent on the phase states, compositions, and concentrations of chemical inclusions.As introducing various chemical inclusions, the initiation of those dynamics mechanisms triggers diverse decay rates of bulk RDX molecules and hereby impacts on growth speeds of final reactions.Results illustrate that adding chemical inclusions can reduce the effectiveness of the void during the shockwave loading.The parent RDX decay rate in CR decreases the most and is about one fourth of that in VR under the shockwave velocity of 9 km/s.In terms of resulting RDX decay rate,it’s indicated that solid HMX and TATB inclusions are more reactive than carbon impurity but less reactive than dry air or acetone inclusions.In general,the less dense RDX system, whose interfacial molecules incline to local hydrodynamic jet, reveals the higher increases in local temperature and stress, the faster intermediate reaction and energy liberation, and the earlier final reaction towards an equilibrium state.It’s suggested that the less dense RDX system has more pronounced responses to the present shock.In addition, the quantitative models associated with a global density characteristic were proposed,which could shed light on estimating decomposition rate and localtemperature rise in crystalline explosives and comprehending shock-induced energy localization under the present intense shockwave loading.Future efforts would be focused on extending the research category towards a large variety of explosives’ family based on various impurity-quantified experiments.And it would be also considered some novel models involving the real physicalchemical interfacial bonding interaction between chemical inclusions and energetic substrates,rather than the present classical heterogeneous explosive model based on the physical doping method.

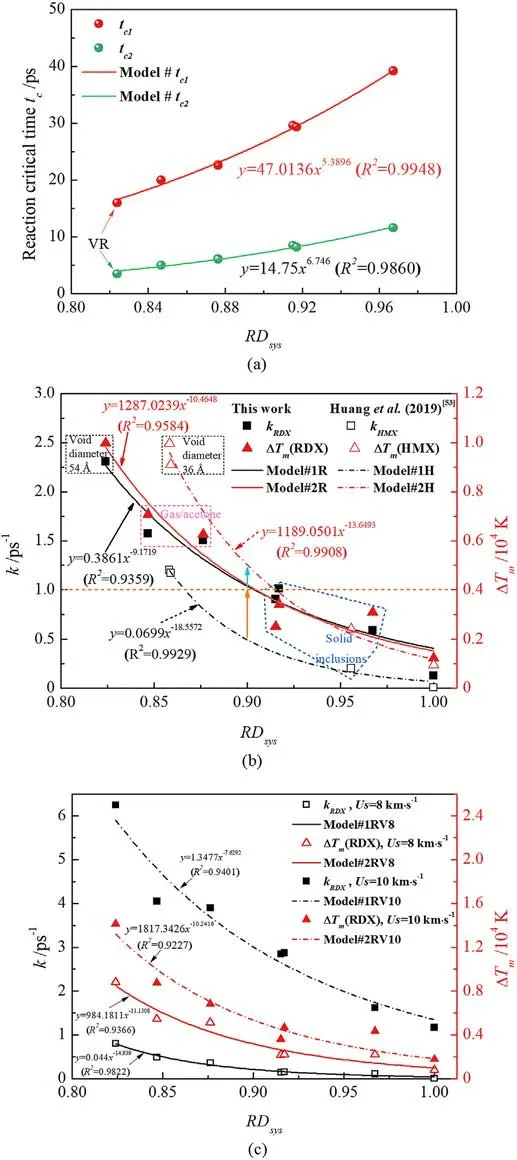
Fig.15.(a)RDsys-related reaction critical-time models in the defective RDX.tc1 and tc2 are the critical time for releasing final products steadily and RDX decay completely,respectively; (b) RDsys-related decomposition rate and energy-localization models(Us = 9 km/s); (c) Models validation for shockwave velocities of 8 km/s and 10 km/s.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors gratefully acknowledge the financial support from National Natural Science Foundation of China(Grant Nos.11872119,12172051,and 11972329)and Natural Science Foundation of Hubei Province (Grant No.2021CFB120).

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.dt.2023.02.011.