基于新课程标准的初中数学教学——以“平行线及其判定”教学设计为例

文| 杨志英

课程标准要求数学课程应致力于实现义务教育阶段的培养目标，即提高学生的数学素养，为其未来的学习和生活奠定坚实的基础。教师需要关注学生的全面发展，特别是逻辑思维能力、创新思维能力和问题解决能力的培养。在课堂教学中，教师可以通过具有挑战性的数学问题引导学生思考和讨论，激发学生的学习兴趣和求知欲；教师还应关注数学与现实生活的联系，让学生在实际情境中理解数学概念和原理，提高他们运用数学知识解决实际问题的能力。同时，教师需要采用多样化的教学方法和手段，如小组合作、探究学习等，以适应不同学生的学习风格和需求。总之，新课程标准下的初中数学教学需要注重学生的全面发展，培养学生的数学思维能力和实际应用能力，加强与现实生活的联系，采用多样化的教学方法和评价方式，以适应不同学生的需求和发展。本文以“平行线及其判定”的教学为例进行说明。

一、教材分析

“平行线及其判定”是人教版七年级下册的内容，课时为2 课时，是在学习了相交线和平行线之后的一节内容，主要探索两直线平行的条件，既是学习几何的基础，也是在学习了角和线之后最基本的知识。其在以后不管是学习三角形、四边形以及后面学习的圆中都是最常用的知识点，所以它是学生数学学习的重点。

二、教学目标

1.学生可以在基本图形中找到内错角、同位角、同旁内角；会在简单的图形中利用直线平行的条件来判断两条直线是否平行。

2.通过观察、操作、想象、推理和交流等活动，培养学生的空间想象力和严格的逻辑推理能力及归纳、总结、概括能力。

3.参与探究知识的形成过程，从而得出结论也就是直线平行的条件，进一步感悟、理解、归纳、语言表达、转化等数学思想方法，深刻体会数学源于生活、用于生活的新课程理念。

三、教学重难点

探索直线平行的条件，掌握直线平行的条件，并能应用这些条件来判断两条直线是否平行。

四、教学过程

（一）问题引入

学生活动：1.欣赏有平行线元素的漂亮图片。（搜集的图片源于生活）

2.画图：根据已知的直线AB 与直线外的一点P，我们利用直尺和三角尺来画出过点P 的直线CD，使直线CD 平行于直线AB，即CD∥AB。（见图1）

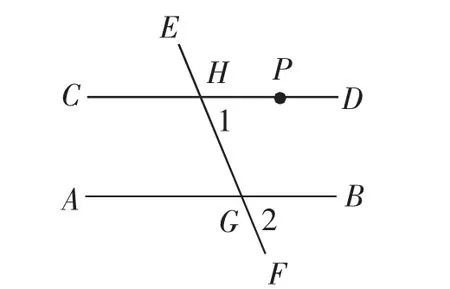
图1

3.反思：我们用三角尺与直尺画平行线时候，你认为三角尺在整个画图过程中起着什么样的作用？（在用三角尺与直尺画平行线的过程中，三角尺的作用是提供与已知直线相交的角度，并保证新画的直线与已知直线平行。三角尺的角度和边长关系可以确保画出的直线与已知直线平行，并且通过调整三角尺的位置和角度，可以控制新直线的位置和方向。因此，可以说三角尺在画平行线的过程中起着关键的作用。

学生先和同桌交流总结的想法，得出结论：利用三角尺画∠PHF，并且使所画的角与∠BGF 相等。（见图1）

教师活动：教师归纳出——相等的两个角和平行的两条直线可以关联起来，那么我们进一步思考——两个角具有什么样的位置关系？

学生回答，引入课题。

（设计意图：此环节是让学生体会到数学知识来源于生活。通过动画渗透本节课的目标，了解线和角的关系，充分体现了新课标的理念。）

（二）合作交流

学生活动：1.结合图画出简化图形（见图2），分析∠1、∠2 有什么位置关系。

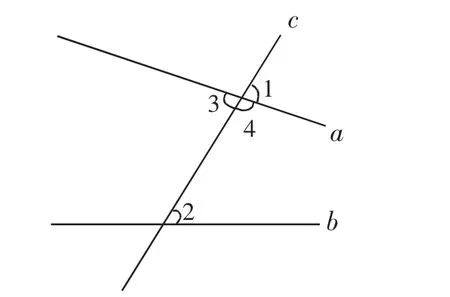
图2

（1）先回答说出∠1、∠2 的方位，同桌互相说出两个角的位置关系，先由一名学生说出，另一名学生补充。

（2）认真观察图形，在图中找出所有的同位角，并将它们准确地标记出来，确保没有遗漏。

（3）观察同位角和邻补角的区别，并把自己的思路说给同桌听。教师再次强调：与对顶角和邻补角不同，同位角在位置上具有特殊关系，其共同特点是：它们都有一条边位于截线c 上。

（4）观察图形（两条直线被第三条直线所截），教师引导学生，在直线a 和直线b 被第三条直线c 所截构成的角中，∠1 和∠2 是同位角，而∠2 和∠3 以及∠2 和∠4 并不是同位角。

我们需要找出∠2 和∠3 之间的位置关系。∠2和∠4 呢？把你的想法说给你的同桌听。

（5）利用几何画板移动直线a 或b 时，我们需要思考∠2 和∠3、∠2 和∠4 的度数是否会随着直线的移动而发生变化，以及它们之间的位置关系是否会改变。

（6）仔细观察图形，在图中找出所有的内错角和同旁内角，并将它们准确地说出来。

（7）归纳概括由两条直线a 和b 被第三条直线c所截，所构成的八个角中的同位角、内错角、同旁内角分别有几对。

教师活动：（1）结合图形指出：同位角——如∠1、∠2；内错角——如∠2 和∠3；同旁内角——如∠2 和∠4。师生同时说出它们分别位于直线a、b 和c 的方位，并简单板书。

（设计意图：本环节设计体现了学生合作交流的意识，在与同伴的交流中，得到三类角，从而充分理解了三种角的分辨方法，在交流中培养了学生的语言表达能力与归纳总结能力，符合新课标的要求。）

学生活动：2.完成练习

（1）指出图3 中的同位角和内错角。

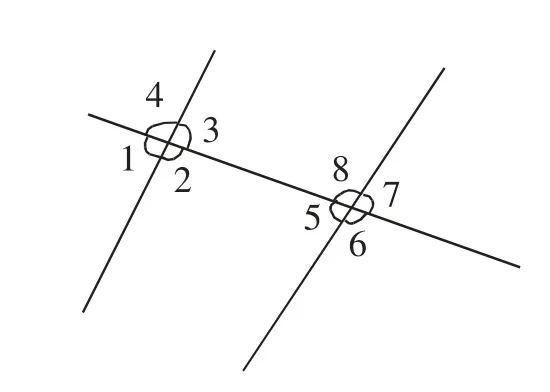
图3

（2）指出图4 中∠1 和∠2；∠1 和∠6；∠6 和∠4；∠2 和∠4；∠A 和∠E 的关系。

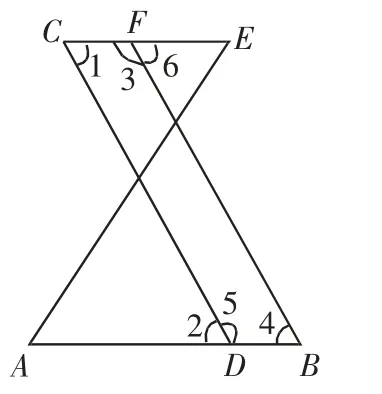
图4

（三）自主探究

学生活动：利用几何画板自己探究，当同位角、内错角、同旁内角满足什么条件的时候，两直线是平行的？

根据表格中的数据，学生归纳、总结，得出结论。一名学生说，其他学生补充，教师板书并帮助学生规范说理过程。

学生利用几何画板测量出图5 中各角的度数，并填写表1。

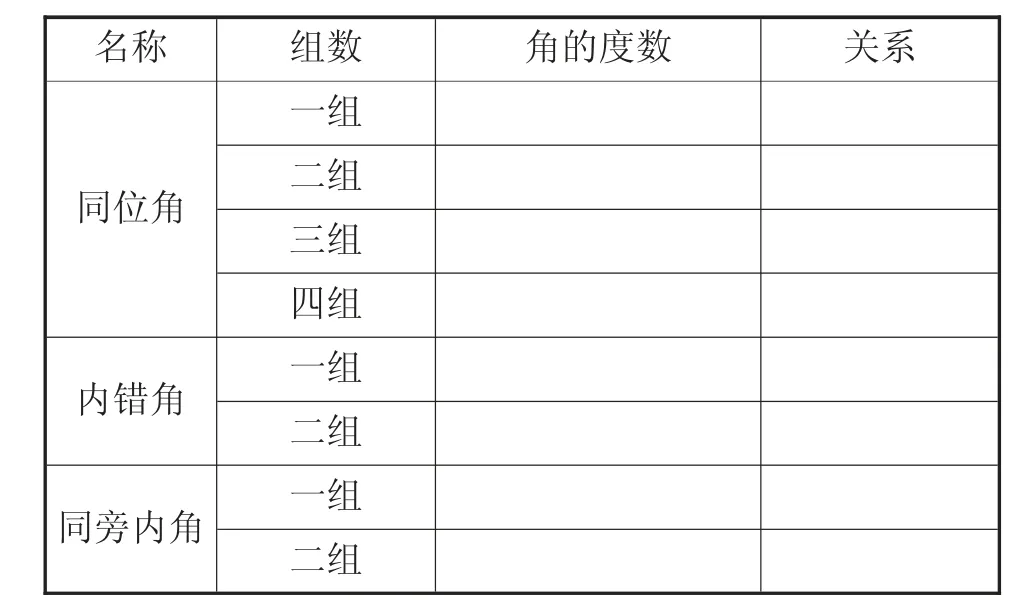
表1

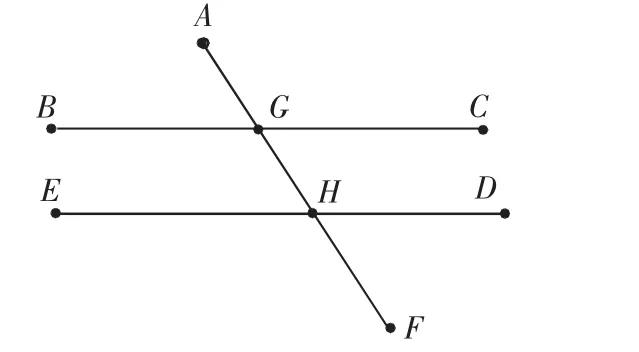
图5

隐藏结论：

1.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行，简单地说成“同位角相等，两直线平行”，即因为∠AGC=∠AHD，所以BC∥ED。

2.两条直线被第三条直线所截，如果内错角相等，那么两直线平行，简单地说成“内错角相等，两直线平行”，即因为∠BGF=∠AHD，所以BC∥ED。

3.两条直线被第三条直线所截，如果同旁内角互补，那么两直线平行，简单地说成“同旁内角互补，两直线平行”，即因为∠BGF+∠EHG=180°，所以BC∥ED。

教师活动：指导学生完成表格，总结直线平行的条件，即平行线的判定。

（设计意图：通过几何画板让学生利用计算机软件自主探究角和平行线的关系，借助表格可以让学生在对比中获取知识，让学生都学有所获。）

（四）课堂练习

1.基础练习（见图6）

图6

（1）∵∠1=_____（已知

∴AB∥CE

（2）∵∠2=_____（已知

∴CD∥BF

（3）∵∠1+∠5=_____（已知）

∴AB∥CE

学生活动：完成问题后，思考：当内错角相等时，两条直线为什么会平行？可以利用两直线平行的判定方法进行解释。

教师活动：巡视，如果学生有困难，可以进行适当的启发、引导。

（设计意图：本环节是在学生知道了平行线判定条件的基础上设计的，体现了讲练结合，让学生及时巩固已经学会的知识，用所学到的知识解决实际问题，体现了数学知识和生活是息息相关的。）

2.提高练习

（1）利用几何画板，验证课本16 页第9 题的结论。

（2）看谁是高手。

如图7 所示，已知∠3=45°，∠1 与∠2 互余，试求出AB∥CD？

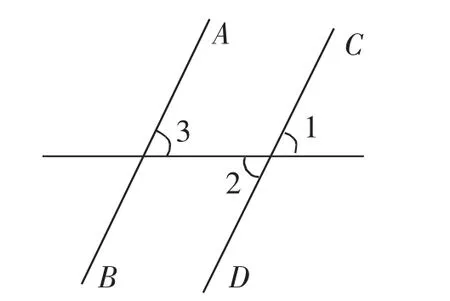
图7

（设计意图：这个环节是个提高的环节，可以使基础好的学生“吃得饱”，也是对平行线判定的一个深化。）

五、归纳总结

让学生回顾本节课的收获，一名学生回答，其他学生纠正、补充。

（设计意图：此环节可以使学生加深对本节课的认识，深化本节课的重难点。）

六、布置作业

在铺设铁轨时，两条铁轨是互相平行的（即阴影部分的铁轨），如图8 所示，已经知道∠2 是直角，那么，再度量图中哪个角（图中已经标出的）就可以判断两条直线是否平行？说出你的理由。

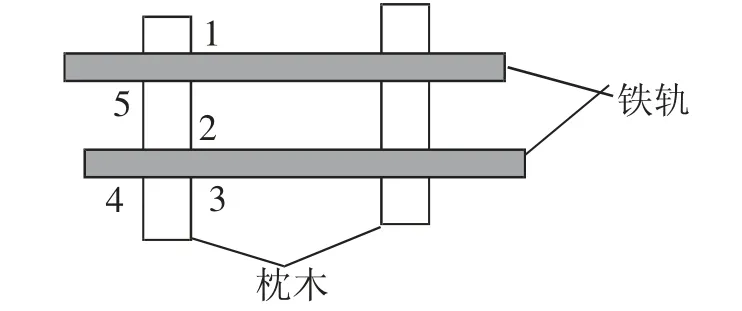
图8

七、教学反思

教师通过PPT 呈现有平行线元素的图片，激发学生对本节课的兴趣，接着设计了合作交流环节，在和学生交流的过程中找到了三类角，再利用几何画板探究了直线平行的条件。整个过程充分体现了学生是学习的主体，教师在教学过程中起到了主导作用。但是本节课有个不足之处，就是学生对几何画板的使用不够熟练，在这个环节上浪费了时间，教师以后要加强学生此技能的训练。