基于需求链的中欧班列开行方案优化
周 露,杨菊花
(1. 兰州交通大学 交通运输学院,兰州 730070;2. 兰州交通大学 高原铁路运输智慧管控铁路行业重点实验室,兰州 730070)
中欧班列开行之初,为开拓市场,各地政府对中欧班列予以较大力度的补贴。近年来,多地政府开始出台中欧班列补贴退坡政策。为使其在补贴减少后,面对海运仍有足够的竞争力,铁路部门需要重视客户需求,提高客户的满意度和忠诚度,充分发挥出铁路在时效性方面的优势,快速抢占中欧高附加值快货运输市场。铁路部门除推行系列简化作业流程的实货制改革方案外,还需编制基于以客户为中心、以客户需求为导向的开行方案,以应对多样化的运输需求,充分发挥铁路运输的优越性。
班列开行方案是在尽可能满足货物运输需求的基础上,科学合理地安排班列的起讫站点、运行径路、编组内容、开行频率等,实现从货流到车流再到列流的组织方案[1]。关于考虑客户需求的研究文献中,张玉召等[2]重点考虑客户需求,以运送最多的货物需求量及最小化客户支出运输成本为目标,构建快捷货物列车开行方案的多目标优化模型。付慧伶等[3]为满足旅客异质需求,制定了周期性列车开行方案。王志美等[4]在列车开行方案编制中,将发到站相同但属于不同客户的车流区分对待,细化了客户满意度。刘晓伟等[5]为适应货主动态需求和运到期限要求,采用动态车流组织方法进行编组方案调整、列车运行方案与车流挂线的综合优化。
对列车开行方案优化的文献中,刘慧婷等[6]基于“备选集”思想优化了临客列车开行方案。周文梁等[7]基于给定候选列车集构造旅客出行网络,进而以最大化列车开行收益为优化目标构建城际列车开行方案优化模型。李晟东等[8]考虑运到期限等货物运输需求,以一天为决策期,编制货物列车的开行方案。史峰等[9]在传统列车开行方案基础上引入列车始发时间,形成高速铁路列车开行方案的新概念。寇玮华等[10]将高铁车站站场基本布局抽象为站场网络图,借助时间序列多品种网络流模式进行行车组织优化。
在构建中欧班列开行方案的目标函数时,双层规划方法得到了很好的应用。赵娟等[11]根据现有的直达、中转2种中欧班列运输组织方式,提出用虚拟弧表示集结过程的广义服务网络构建方法,提出考虑集结时间的中欧班列直达与中转运输优化模型。王臻杰等[12]基于混合轴辐式网络理论,建立双层规划模型。徐安策[13]通过交通流量平衡理论,构建双层规划模型,上层是以运输企业效益最大为目标的整数规划模型,下层为基于用户平衡理论的流量分配模型。Qi等[14]分析口岸集并与干支结合模式对中欧班列运输组织协调、服务网络优化的重要影响,构建了中欧班列服务网络优化的双层规划模型。
其余研究中欧班列的文献中,冯芬玲等[15]提出一种基于改进TOPSIS法及灰色关联分析的评估方法,对多层网络关键节点进行识别,然后利用动力学传播模型检验识别结果的有效性。洪治潮等[16]研究在区块链背景下中欧班列网络配流问题,并且采用两阶段博弈刻画区块链技术应用前后班列运价变化。徐菱等[17]立足于高、低值货主在运输价格和运营平台服务质量偏好上的差异,构建由政府、运营平台和货主组成的三级博弈模型。邢磊等[18]针对海陆联运与不确定空箱需求等中欧班列空箱调运问题,采用分布式鲁棒机会约束规划研究不确定环境下的多周期中欧班列空箱调运优化问题。张得志等[19]研究需求不确定下中欧班列国际运输网络设计优化。
上述研究为中欧班列开行方案设计和优化提供了借鉴,但也可以看出,既有研究一般是从客户需求这一个点展开,属于需求侧管理,并未将需求链管理思想融入班列开行方案中。需求链管理是按照从终端客户到供应商的顺序对整个供应链的协调与管理,扩展了传统的供应链管理的概念,核心是强调满足客户实际需求,创造卓越的客户价值。本文基于需求链管理思想,构建双层规划模型,上层模型从铁路运营方角度出发,在轮廓计划指导下,利用“备选集”思想,以调整班列始发时间为切入点,组织班列集中于星期“几”灵活开行,达到运输效益最大化的目标;下层模型根据实际客户需求,拓展为允许货流拆分的物流服务选择模型。通过上下层模型的交互,体现供需双方在市场中的博弈行为,从而实现需求链管理思想在中欧班列开行方案中的运用。
1 模型构建
1.1 问题描述
本文基于“一弧多服务多货流”网络构建中欧班列开行方案双层规划模型,“一弧”指一个运输弧段;“多服务”指运输弧段对应的多个物流服务;“多货流”指订单可以拆分。在需求链中,货物的运输费用、仓储费用以及包装费用占物流总成本比例约为90%,因此文中铁路运营方提供的物流服务主要包括货物运输服务、仓储服务和包装服务三部分。不同种类的货物包装费用有差别,其中包括了包装费用和人工费用两项,在文中统一规定包装服务费用的占物流服务费用的20%。物流服务方案在物流服务的基础上具体到中欧班列开行车次和始发于星期“几”的发车时间。模型实施流程如图1所示。

图1 模型示意图
1.2 模型假设
1) 本文采用“点对点”直达与集结转运直达两种开行模式。
2) 忽略实际货运作业站的复杂关系,视区域为节点,且所有节点均具有车组甩挂和班列中转的作业能力。
3) 中欧班列运输过程中所有的节点、集结中心以及运输路线都已知。
4) 货运量、货运需求量等均采用20英尺标准集装箱计算。
1.3 参数定义
1.3.1 集合定义
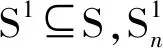
1.3.2 决策变量
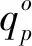
1.4 模型构建
1.4.1 上层模型
1) 目标函数
上层目标函数将碳排放费用纳入铁路运营成本中,以铁路运营方收益最大为目的,表达式如下:
Z=Max(Z1-Z2-Z3)
(1)
式中:Z1为运营方的营运收入,当订单o的货物选择中欧班列s∈S1的物流服务方案p时,客户向中欧班列运营方支付的费用,Z2为运输成本,包含运输过程中的固定成本与可变成本,Z3为碳排放成本。
(2)
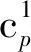
(3)
式中:c1为物流服务s∈S的固定成本,单位:元/TEU,c2为物流服务s∈S的可变成本,单位:元/km,ls为物流服务s∈S的运输距离,单位:km。
(4)
式中:ctax为针对温室气体征收的碳税,单位:元/kg,Es为中欧班列s∈S1的碳排放量,单位:kg/TEU·km 。
2) 约束条件
① 货物运输时间限制
(5)
式中:Tmin为物流服务方案的运到时间上限,单位:h,Tmax为物流服务方案的运到时间下限,单位:h,vs为表示中欧班列运行的平均速度,单位:km/h。
② 碳排放总量限制
(6)
式中:E为一批货物运输过程碳排放总量的限制,单位:kg。
③ 能力约束
式(7)为弧段能力约束,表示任意弧段开行的中欧班列数量不超过其每昼夜班列通过能力,式(8)为节点能力约束,表示物流服务中的实际货运量不超过节点最大作业能力。
(7)
(8)
式中:fij为弧段每日昼夜班列通过能力,单位:列/d,qmax为节点最大的作业能力,单位:TEU。
④ 供需平衡约束
订单选择的物流服务方案中的货运量与货运需求量相等。
(9)
式中:ζo为订单o∈O的货运需求量,单位:TEU。
⑤ 计划约束
式(9)表示中欧班列固定于“星期n”开行,其中“小于等于号”表示允许落空不盈利的发车计划,如开行第一周星期二的班列,但落空第二周星期二的班列。
ys≤zn,n∈N,s∈S1
(10)
⑥ 决策变量约束
ys∈{0,1},∀s∈S1
(11)
zn∈{0,1},∀n∈N
(12)
1.4.2 下层模型
1) 目标函数
下层模型以最小化客户物流费用为目标。表达式如下:
W=Min(W1+W2+W3)
(13)
式中:W1为物流服务费用,当订单o选择某一物流服务方案p运输时支付的费用,W2为货物全程运输时间成本,W3为集结等待时间成本。
(14)
式中:cp为物流服务s∈S的运价,单位:元/TEU,ξ为折扣系数,客户选择物流服务时,铁路运营方根据货运需求量与物流服务内容给出不同的折扣。
(15)
式中:c3为订单o∈O在运输途中的单位时间成本,单位:元/TEU·d,tp为物流服务方案p∈P到达目的地的日期,to为订单o∈O运输需求的产生日期。
集结等待时间成本为货物集结等待时间与时间价值系数的乘积。货物等待时间表达式借鉴文献[20]。
(16)
式中:Ψ为时间价值系数,单位:元/TEU·d,ωp为物流服务方案p∈P的中欧班列开行频率,单位:列/周。
2) 约束条件
① 客户物流服务方案数量选择约束
表示货流在运输途中可以拆分,并给出了各订单可选方案的最大数量。
(17)
式中:δo为订单o∈O可以选择物流服务方案的最大数量。
② 货流限制
表示实际运输中的货运量在所选择的物流服务方案的服务能力范围之内。
(18)
式中:hp为物流服务方案p∈P的载运能力,单为:TEU。
③ 决策变量约束
(19)
(20)
2 求解算法
2.1 备选集生成策略
生成备选物流方案的本质即资源约束下的最短路问题,客户的备选物流服务方案即备选路径。一般而言,客户都希望货流能够通过最短路进行运输。由于路网运输水平限制,客户并不总能选到最理想的物流服务,所以除了最短路,还需找到一定数量的次优路径以供客户选择。备选集的构造目标是选出路网中所有可能开行的班列,其规模大小直接影响到模型求解效率,因此要合理控制备选集规模。
对备选集的组成要素进行分析,首先确定路网上的列车OD、径路,其次在这些班列开行径路上形成备选班列开行方案。中欧班列开行方案的备选集是由若干个备选运行区段构成的集合,备选运行区段是指任意2个具有始发终到能力的节点之间的区段。在优化班列开行方案时,全部班列运行区段都限制于备选集中。本文在确定中欧班列开行方案时,先采用K短路算法求出每一个OD对间的备选径路。步骤如下:
步骤1:根据Dijkstra算法求得起点i至终点j间的最短径路,并将其放入到集合S中,令I=1;
步骤2:取集合S中的最后一条径路I作为当前径路,将该径路中除j点之外的每个节点k作为潜在的偏离节点,计算出k至j间的最短径路。为了满足径路无环并避免径路重合等两个限制条件,该径路不能够经过当前径路上从节点i至节点k之间的任何一个节点,同时该径路上从节点k发出的边不能够与集合中已有的各最短径路从k发出边相同;
步骤3:在求得各偏离节点k至j的最短径路后,将其与当前径路中的从i至k的径路连接,作为第I+1条最短径路的候选,并将其加入集合S中;


2.2 粒子群算法概述
粒子群优化算法(particle swarm optimization,PSO),是由James Kennedy和Russell Eberhart提出的一个简化算法模型改进形成。PSO算法的思想源于对鸟群觅食行为的研究,鸟群通过集体的信息共享使群体找到最的目的地,是一种基于种群的全局随机搜索算法。在PSO算法中,一个优化问题的解相当于探索空间中的一只鸟,称之为“粒子”。算法通过随机初始化粒子,然后反复训练探索最优解,并且在每一次训练中,首先更新粒子速度和位置信息,然后根据计算到的结果改变粒子的个体最优解和全局最优解。PSO算法具有收敛速度快、参数少、算法简单易实现的优点。基本算法(速度位置计算公式)为:
(21)
(22)
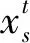
2.3 拉格朗日松弛算法基本原理
拉格朗日松弛算法的核心思路是对模型中的约束条件进行复杂度分析,选择其中对计算规模和可行域影响较大,导致模型求解复杂度提高而难以求解的约束条件作为复杂约束,通过引入拉格朗日乘子与约束条件构建罚函数,并将其添加至目标函数中。约束条件的吸引过程模型仍然保持线性,从而构造原问题的松弛问题和对偶问题。由于原问题中复杂约束成为了目标函数的一部分,表现为目标函数的惩罚值,因此约束条件可以被违反,从而扩大了原问题的可行域,并且由于对松弛处理的约束条件中的决策变量约束判断过程计算量大幅度下降,使得模型计算量也随之下降,使得问题的求解难度降低。
2.3.1 拉格朗日松弛算法关键步骤
1) 松弛模型构建
对下层模型中的约束条件进行分析,式(18)为复杂约束,引入一组非负的拉格朗日乘子α,根据以上拉格朗日乘子,则可以得到原问题的松弛问题LR。
(23)
s.t.α≥0
(24)
2) 对偶问题构建
将原问题进行松弛处理后,对于给定的任意α≥0,β≥0,松弛问题LR转化为可以进行最小值求解的线性规划问题。由于该问题的可行域完全包含了原问题可行域,同时包括了一部分原问题的不可行解,因此构造拉格朗日对偶问题LD。
LD=Max LR
(25)
通过松弛问题和对偶问题的构建,原问题的求解过程转化为了对偶问题LD与松弛问题LR的双层优化问题。对于松弛问题LR,在当代的拉格朗日乘子条件下对问题进行求解,获取的最优值是原问题的一个可能的下界,并将其传递给对偶问题,用于判断算法下一步的执行步骤。对于对偶问题LD,将接收的松弛问题最优值与当代对偶问题最大值进行比较,根据比较结果确定算法步骤,并且根据预先设置的拉格朗日乘子更新法则更新每一代的拉格朗日乘子用于迭代计算。按照上述流程迭代直至对偶问题达到收敛或满足停止条件后,此时对偶问题当代的最优值,可以认为是原问题的最优下界解。
3) 拉格朗日乘子更新法则
算法选择常用的次梯度法作为拉格朗日乘子的更新法则,次梯度法是根据弧段占用信息,对“惩罚费用”与“占用价格”迭代更新,实现弧段资源的动态定价,继而影响货流与物流服务在下次迭代中的路径选择。通过对“资源定价”与“路径选择”过程的反复迭代,最终得到货流需求与物流服务之间的最佳时空映射关系。更新法则的计算过程如式(26)所示。
(26)
式中:αn为进行第n次迭代的拉格朗日乘子,ϑn为松弛问题LR在当前拉格朗日乘子条件下所对应的次梯度,计算公式如如式(27)所示。
(27)
式中:ln为第n次迭代的步长,算法设置ln=τ/2n+1,其中τ为步长调节因子,取值根据需求选择合适的正值。
4) 算法终止条件
在拉格朗日松弛算法的基本框架中,通常将次梯度ϑn=0作为算法的停止条件,但在实际迭代过程中松弛约束选取、迭代步长等因素都会影响到算法的收敛速度,可能导致在有限的迭代次数内不满足所有拉格朗日乘子对应的次梯度都为0,这一终止条件。因此,在对次梯度判断的基础上通常设置其他的终止条件对算法的迭代次数进行限制,本文设置以下两个终止条件:
a、设置容许误差值ε,当满足|ϑn|<ε时,终止算法,ε一般为非负数;
b、设置最大迭代次数N,当算法迭代至设置的最大迭代次数N时,终止算法,N为正整数。
5) 求解下届解算法流程

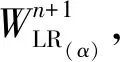

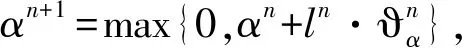
Step5:算法终止。输出原问题的最优下界解和最优目标函数值,并检验解的可行性。
本文构建的中欧班列开行方案双层规划模型为非线性规划问题,且中欧班列路网规模庞大,采用精确算法较为困难。根据本文模型特点,采用粒子群算法对上层规划模型求解,并嵌入拉格朗日启发式算法对下层模型求解。具体算法设计如图2所示。

图2 中欧班列开行方案算法设计图
3 算例分析
3.1 算例背景
中欧班列有西、中、东、南四条通道,本文以规模最大的西通道为案例研究范围,并选13个中欧班列节点城市、4个港口,1个口岸站(阿拉山口),1个目的地(德国汉堡),具体情况如图3所示。中欧班列与远洋海运之间形成竞争关系。
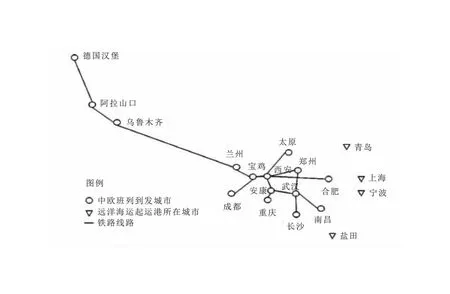
图3 中欧班列运输网络拓扑结构图
为方便Matlab编程,将各个节点城市用字母代替,如表1所列。
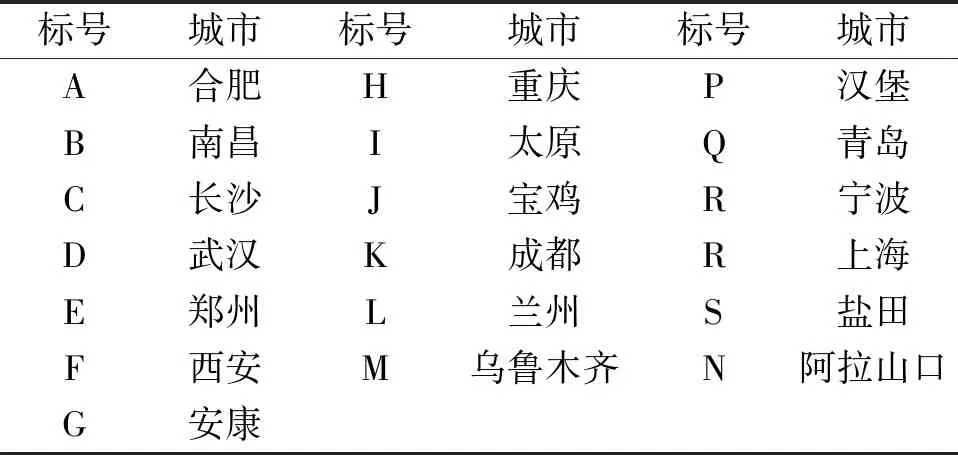
表1 节点城市编号
3.2 算例数据
关于碳税的取值,环保部给出的建议为20元/t,故在本文中取值0.02元/kg,其他数据为参考已有研究后的综合取值,具体数值如表2所列。

表2 参数列表
3.3 算例结果分析
本文采用粒子群算法求解上层规划模型,并嵌入拉格朗日启发式算法求解下层模型,根据表6的订单案例进行计算,迭代700次,得到全局最优解。使用2.1节备选集生成办法后,得到备选方案456个,各订单均可在12 s内找到最优服务方案,Gap为0.00%时所得结果为最优解,表明同时满足铁路运营方收益最大和客户物流服务费用最小,得到最优目标函数值为66 010 353.9元。优化结果趋势图如图4所示。
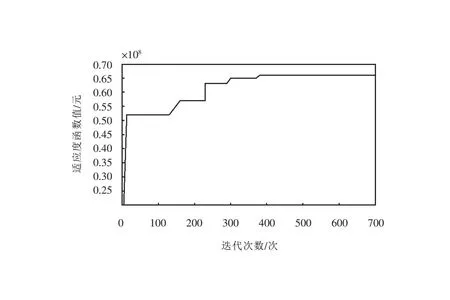
图4 优化结果趋势图
50位客户所需物流费用具体如图5所示,从图5中可看出,货物物流服务费用在总物流费用占比较大,若能减少此项费用支出,物流总费用也会大大降低,这也是铁路运输竞争优势所在。

图5 客户费用分析图
1) 货流可拆分结果对比分析
将货流不可拆分与货流可拆分情况对比,具体情况如表3所列。订单拆分放宽了中欧班列对客户货运量的要求,减轻了货代的货源组织压力。为服务更多货流,班列开行频率大大增加,中欧班列营运收入增加35.94%,运输成本增加31.4%,碳税增加12.4%,利润提高41.67%。

表3 结果对比分析
2) 上下层模型博弈结果对比分析
运营方收益最大与客户物流费用最低在一定程度上是相互博弈的关系,同时满足两者最优是不切实际的,一个目标结果越优,会导致另一目标与预期结果背离,故应寻求一个令两者都满意的均衡状态。本文分别将只考虑运营方收益最大和只考虑客户物流费用最小两种情况对比,结果如表4~5所列。
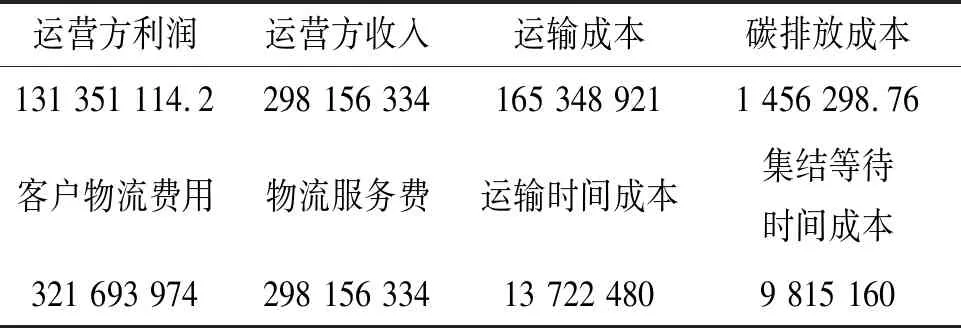
表4 只考虑运营方利润最大的求解结果
通过表4、表5的对比分析可知,单一追求运营方利益最大,将导致客户选择物流费用相对较少、运输时间长的远洋海运;单一追求客户物流费用最小,会造成铁路运营方落空不盈利的中欧班列发车计划。因此本文算例中求解出的运营方利润与客户物流费用为两方博弈后的平衡点,所得结果更符合实际情况,也更加合理。
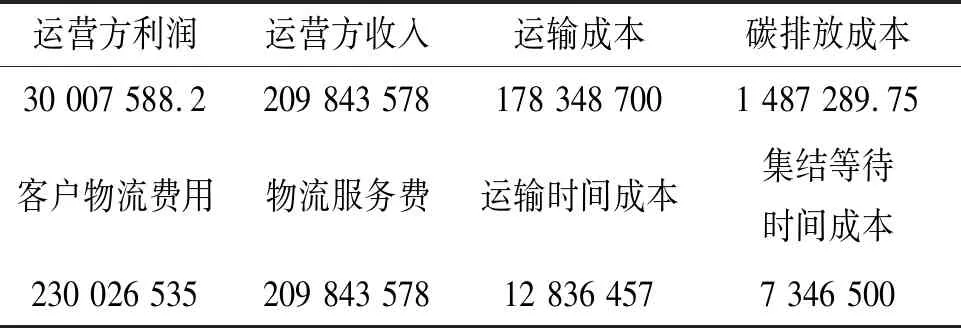
表5 只考虑客户物流费用最小的求解结果
订单案例为随机生成,各个订单中的货运需求量符合均匀分布U(10,100),运到期限符合均匀分布U(20,60),具体情况如表6所列。

表6 订单案例
通过表6可知,本文订单总货运需求量为2 801 TEU,算例中选择中欧班列物流服务达到100%。结果表明,相较于海运,中欧班列的运输时间短,运价低,物流服务更受客户青睐。优化后的中欧班列开行方案如表7所列。
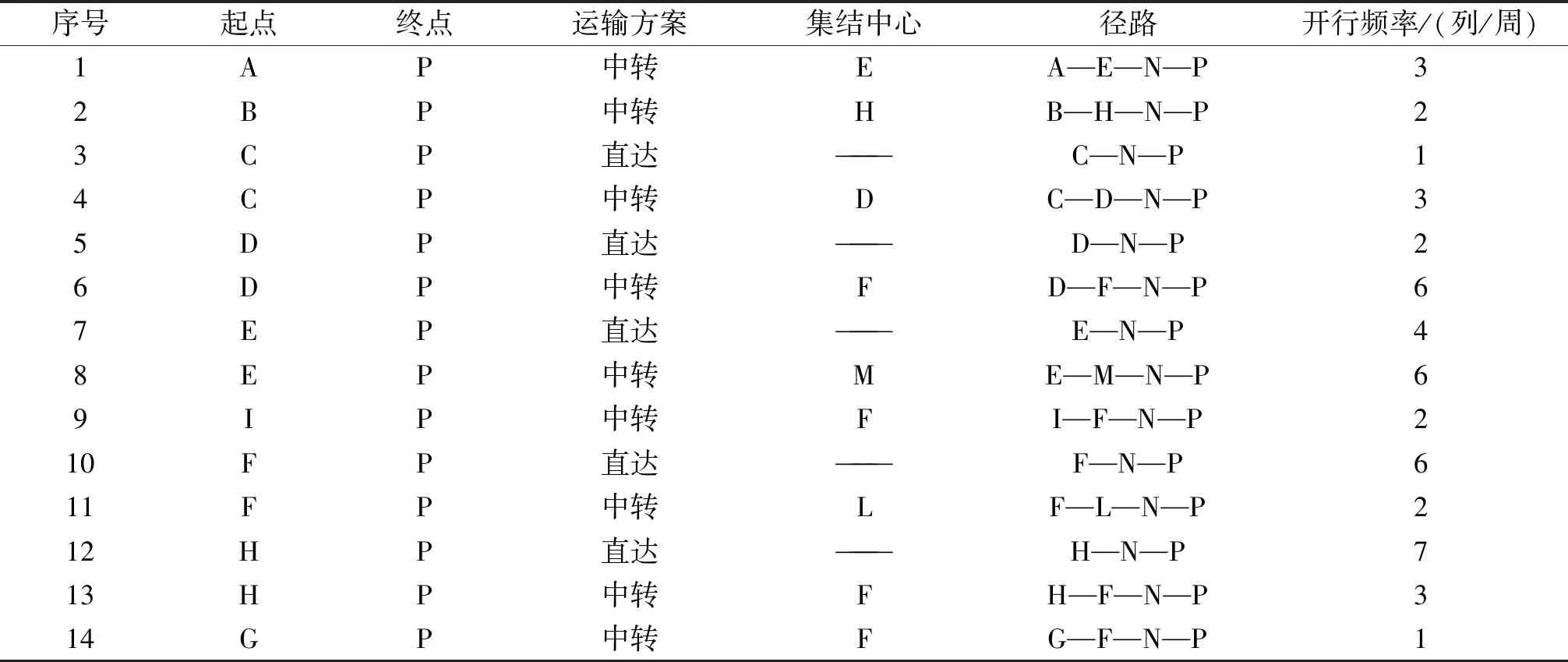
表7 中欧班列开行方案
4 结论
1) 本文研究了基于需求链的中欧班列开行方案优化问题,为实现需求链管理思想在班列开行方案中的作用,构建了双层规划模型。上层模型以铁路运营方利润最大为目标,在轮廓计划指导下,允许落空不盈利的中欧班列开行方案,并且根据客户货运需求报价;下层模型以客户物流费用最小为目标,根据实际情况可允许货流拆分,进而拓展为物流服务选择模型。通过上下层模型的交互,体现供需双方在市场中的博弈行为,从而实现运营方利润与客户物流费用的均衡。
2) 文中利用粒子群算法对上层模型求解,并且嵌入拉格朗日松弛算法求解下层模型,通过50个订单案例优化中欧班列开行方案。对比分析货流可拆分与货流不可拆分情况下铁路运营方营运收入、运输费用、碳税与利润的变化,可充分证明本算法的合理性与优越性。
3) 在制定开行方案时运用备选集思想,根据K短路原则生成一定备选集,可有效提高求解效率,但是中欧班列开行备选集的完备性与合理性对优化结果有一定影响,对于班列备选集的生成策略尚待进一步完善。

