水滴撞击倾斜非Newton除冰液液膜动力学行为特性数值研究*

崔 静, 岳茂昌, 牛书鑫, 杨广峰

(中国民航大学 航空工程学院, 天津 300300)

0 引 言

民航地面除/防冰作业的高效性和高可靠性是影响航班飞行安全和准点率的关键因素,机场在进行防冰作业时,地勤人员需要向飞机机身喷洒除冰液,形成一层薄液膜以阻止和延缓飞机表面在一定时间内再次结冰[1]．在雨天除冰液保持时间会大幅度缩短,更易危害飞行安全．因此,分析空气中水滴撞击机身除冰液液膜这一物理过程,对研究除冰液的失效行为具有重要意义．对于液滴撞击液膜这一现象,目前主要通过高速相机和计算机模拟技术来实现对这一过程的研究．

Cossali等[2]通过采集撞击的运动过程,定性和定量地分析了撞击后的多种状态．之后许多学者发现,改变流体的黏度、表面张力等物性参数对液滴的各种状态的发生具有重要影响[3-8]．通过实验的方法虽然能够直观地观察撞击过程的形态变化,但撞击过程中流场的速度、压力、物性的变化等难以通过实验具体观察,因此许多学者采用数值模拟的方法对流场内部的一些变化进行研究．一些学者利用LBM方法[9-11]建立了流体运动的数值模型;另一些学者使用VOF方法[12-15]捕捉气液界面,建立了液滴撞击的数值模型,这些数值模型的使用对于分析撞击过程中速度场、压力场等物理场的变化提供了新的手段．然而以上的研究主要关注于Newton流体下液滴撞击的现象,实际用于飞机防冰的除冰液是一种非Newton流体．在非Newton流体的研究方面,一些学者开展了黏弹性[16]、屈服应力特性[17]、剪切增稠型[18]、剪切变稀型[19]等具有非Newton流变特性的液滴撞击固体壁面的研究．这些研究表明,撞击过程流体的动态黏度直接作用于液滴的动力学行为,这与Newton流体的液滴相比表现出极大的不同．而在非Newton流体的数值模拟研究中,为了准确描述它们的流变特性,需要采用不同的数学模型．其中,王强等[20]和张亚博等[21]使用幂律模型拟合出了Ⅱ型和Ⅳ型除冰液的流变特性曲线,为构建水滴撞击非Newton除冰液液膜提供了理论基础．而在幂律流体的数值研究方面,一些学者采用修正的幂律公式[22-24]开展了非Newton型流体中液滴撞击、液膜破碎、液膜形成等方面的研究．这些研究为深入理解非Newton流体的动态行为和流场分布提供了重要的技术手段和理论参考．

针对水滴撞击非Newton除冰液这一问题,本文耦合相界面控制方程及组分输运方程构建了水滴撞击倾斜除冰液液膜的数值模型,研究了撞击过程中的动力学形态演变和液膜物性变化．进而与实验结果相对比,讨论了斜面坡度和非Newton特性对撞击过程的影响,以及水分在除冰液内的质量扩散状况．在数值计算得到的液冠半径和生长速度的基础上,分析了不同坡比下液膜对液滴形态演变的作用规律．

1 数值计算方法

为了准确分析液滴撞击机身除冰液液膜这一动态过程,将曲率多变的飞机表面看作是倾斜的固体壁面．当空气中的水滴撞击除冰液液膜时,会发生溅射、铺展、互溶等物理过程,导致液膜抑冰失效．这一复杂的行为过程是一种多相(空气-除冰液-壁面)、多组分(水-除冰液)、多体系(Newton流体-非Newton流体)耦合作用的复杂微物理过程．

为了描述此复杂的物理过程,将水、除冰液和空气视作不可压流体,构建的数学模型除包含常规的流动控制方程外,还包括以下子模型: 1) 多相流模型,将液滴和液膜看作同一液相,采用VOF法求解撞击过程中液滴与液膜在空气中的相界面形成和迁移; 2) 组分输运模型,将液滴和液膜看成是同一液相中具有不同组分的混合物,采用不带化学反应的组分输运方程求解撞击过程中液滴与液膜的质量传递; 3) 湍流模型,在剪切变稀流体和液滴撞击倾斜壁面的数值计算中,郑所生等[24]和Qiu等[25]采用RNGk-ε湍流模型进行了模型构建．本研究中下落水滴的Reynolds数较大(Re>4 000),我们假设水滴撞击倾斜非Newton液膜的过程具有湍流特性,选取了RNGk-ε模型作为本研究的湍流模型．具体控制方程如下．

1.1 多相流模型

在VOF方程中通过求解液相体积分数的连续性方程来实现对液相与气相界面的跟踪．对于q相,该方程具有以下形式:

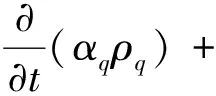
(1)

其中ρq是q相的密度,vq是q相的速度矢量．体积分数方程不求解空气相,但提供各相体积分数的约束:

(2)

在每个控制体积中,所有相的体积分数总和为1．因此,任何给定单元中的变量和特性要么纯粹代表相之一,要么代表液相和气相的混合,这取决于体积分数值．VOF法只求解一个动量方程,得到的速度场为所有相共享:

(3)

其中F是由表面张力引起的附加体积力．液体的表面张力采用连续表面张力模型(CSF)计算,其具体形式为

(4)

其中σ为表面张力系数,kl为液相与气相之间的表面曲率,ρ为体积分数平均密度,ρl为液相密度,ρg为气相密度．

1.2 质量扩散模型

(5)

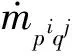
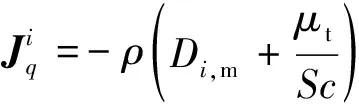
(6)

其中Di,m是混合物中组分i的质量扩散系数,DT,i是热扩散系数,Sc是湍流Schmidt数,μt是湍流黏度．

1.3 湍流模型

RNGk-ε模型是通过重整化群论统计技术推导的,它的形式与标准的k-ε模型相似,但RNG模型的ε方程有一个额外的项(Rε),提高了快速应变流的精度,并且与高Reynolds数的标准方程相比,它提供了一个解释低Reynolds数效应的有效黏度(μeff)微分公式．两方程的湍流模型通过求解两个独立的输运方程来确定湍流的长度和时间尺度．RNGk-ε模型通过湍流动能k及其耗散率ε由以下输运方程得到:

(7)

(8)

其中,Gk表示由于平均速度梯度而产生的的湍流动能,Gb为浮力产生的湍流动能,YM表示可压缩湍流的波动膨胀对总体耗散率的影响,C1ε,C2ε,C3ε为常数,αk和αε分别是k和ε的湍流Prandtl数,Sk和Sε分别是自定义的源项．

2 模 型 构 建

2.1 模型简化及假设

对于液滴撞击液膜这一过程的计算,考虑液滴、液膜以及周围气体的流动,定义气相为主相,液相为水和除冰液的混合物,在计算初始化时,分别给水滴区域和液膜区域设置不同的组分质量．如图1所示,计算域大小为20 mm×10 mm,整个计算域分为3个区域,分别是:液滴区域,其内部流体设置为水和除冰液的混合物,在初始化时设置为100%的水;液膜区域,其内部流体也设置为水和除冰液的混合物,根据实验的不同工况,设置不同的质量分数;其他区域的流体设置为空气．假设液滴为标准球形竖直下落,水滴的初始直径为d,下落速度为v,重力加速度为g=9.81 m·s-2．壁面上覆盖有非Newton除冰液液膜,定义中心点的左侧为液膜下游,右侧为液膜上游．撞击产生的液冠下游半径为Sd,液冠上游半径为Su．底面边界设置为固体倾斜壁面,其他为气体边界．斜面的坡度为

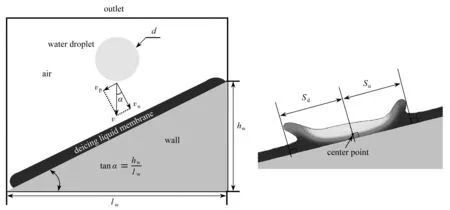
图1 物理模型Fig. 1 The physical model

tanα=hw/lw．

(9)

图1中的vn和vp分别表示液滴下落速度v在斜面法向和切向的分量:

vn=vcosα,vp=vsinα．

(10)

2.2 材料参数

液滴撞击液膜的过程中,流体的运动涉及多个物理量和参数．为了使得不同条件下的撞击过程能够进行比较和实验,引入如下几个无量纲数来描述问题．描述惯性力和表面张力相对关系的Weber数

We=ρv2d/σ;

(11)

描述惯性力与黏性力相对关系的Reynolds数

Re=ρvd/μ;

(12)

撞击的无量纲时间

t*=tv/d,

(13)

其中ρ,v,d,σ,μ分别为水滴的密度、速度、直径、表面张力、黏度．

王强等[20]和张亚博等[21]经过测试指出幂律模型能较好地拟合出Ⅱ型除冰液的流变特性,为了探究除冰液液膜非Newton流变特性对液滴撞击过程的影响,本文采用在工程上被广泛使用的幂律方程来描述除冰液液膜流变特性的变化,其方程如下:

τ=kDn,

(14)

式中τ为剪切应力;k为稠度系数,其与流体稠度有关;n为流态特性指数．

在本文中所模拟的Ⅱ型除冰液液膜和水的具体物性参数见表1．

表1 材料物性参数

3 计算结果及分析

3.1 液滴撞击倾斜液膜的动态过程及分析

图2为液滴撞击坡比为5/20的倾斜液膜后的动态过程,其中液滴速度v=4 m/s,直径d=2 mm,Weber数We为408.3(模拟)和397.5(实验),液膜的除冰液初始浓度为0.5,液膜的厚度为0.5 mm．

(a) 数值模拟结果(a) Simulation results

从图中可以看到,液滴撞击液膜后产生的液冠在中心点两侧呈现出明显的非对称特征,随着时间的推移,这种非对称性进一步增强．由于液滴撞击液膜这一过程,不仅会产生外在的形态变化,而且两种不同物性的液体会相互扩散．因此采取实验的手段无法满足对撞击过程中流体内部变化研究的需求,为了进一步研究液滴与液膜在撞击过程的内部变化,我们通过数值模拟的手段观察了水和除冰液的质量分布云图,如图2(a)所示．图中浅蓝色区域代表液体的成分为水,而深蓝色区域代表除冰液．根据图2展示的液冠形态随时间变化的模拟计算结果(图2(a))和实验结果(图2(b))可以发现,我们构建的数值模型很好地恢复了液滴撞击液膜后形成的液冠,以及液冠表现出的非对称特征,这表明该模型的宏观结果可以满足分析的需求,能够对液滴撞击液膜后的形态演化进行有效预测．

如图2(a)所示,在撞击的初始阶段液滴与液膜开始接触(t*=0),由于流体表面张力的作用,液滴与液膜难以相互渗透,这时可以发现水分与除冰液两种物质之间的界面清晰可见．随后在惯性力驱动下液滴快速向下冲击液膜(t*=0.46),受流体黏性力和表面张力的作用,液滴与液膜交界面附近的液体开始以圆弧形式向上弯曲,形成一个初始的液冠．从质量分布图中可以观察到,液冠的外壁比内壁的颜色更深,这说明外壁含有更高浓度的除冰液成分．这种现象暗示着液滴撞击产生的液冠是由液滴和液膜的部分流体组成的,并且在液冠的形成过程中,可能存在着除冰液被带离液膜的情况．随着冲击过程的继续(t*=1.62～3.22),液滴受到周围液膜的挤压,引起剧烈的对流运动,从而加速液滴中水分与液膜中的除冰液传输与混合．同时受液滴径向运动的影响,液膜内部的液体将从撞击区域向两侧扩散．

随着撞击过程的继续,液冠的非对称特征将更加显著,在t*=3.22时可以看到下游液冠半径Sd明显大于上游液冠半径Su．并且在t*=4.82～6.22(图2(a))和t*=7.31(图2(b))时,上游的液冠已经开始回落,然而下游的液冠仍在向左侧扩张．运动间断理论认为,在液滴撞击液膜的过程中,撞击区域内流体的径向流动速度要远高于液膜内的流动速度,在速度间断的作用下,液体会持续不断地流入液冠,进一步促进液冠的发展[26]．这一理论表明,流体内的速度变化会对液冠的形成和发展产生重要影响．经过分析认为,产生这种不对称现象的原因是流体运动的不对称．由于倾斜壁面的影响,液滴与液膜之间的撞击是一种非法向撞击行为,液滴撞击液膜时将产生一定夹角,这导致撞击后液滴向上游和下游传递的动量不同,并且上游的运动需要更多的能量克服液膜的阻力以及液冠自身的重力,这将进一步降低上游流体的速度．而剧烈的运动则会加快除冰液的扩散,因此从图3(a)中可以看到上游液冠的颜色比下游液冠的颜色更深,这说明上游液冠的除冰液浓度更高．为了进一步验证,我们选取了t*=3.22时中心点8 mm范围内的速度分布,如图3(b)所示．在整个范围内,可以观察到上游流体的速度明显低于下游流体的速度．此外,随着距离的增加,流体速度呈现先增大后减小的趋势,并在距离中心点约2 mm处出现一个速度峰值．经研究发现,该速度峰值位于气体夹带形成的小气泡边界上,我们通过对气泡运动轨迹的观察,推测这可能是液冠与液膜的边界．

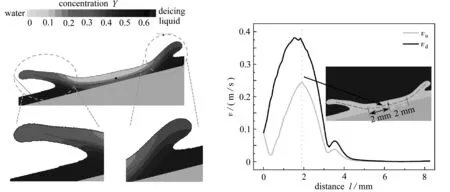
(a) 质量分布 (b) 速度分布(a) The mass distribution (b) The velocity distribution

3.2 液膜的非Newton流变特性

事实上,液滴在倾斜液膜上的非法向撞击行为,不仅造成上游和下游的动量传递差异,还将改变液膜在上游和下游的黏度．研究表明,液膜的黏度对撞击过程中的动力学行为有显著影响[3-4,8]．由于液膜内的除冰液是一种具有剪切变稀特性的非Newton流体,即它的黏度随剪切速率的增加而逐渐降低．液膜的黏度越高,液体分子之间的作用更强,这将导致内部的剪切力越大,从而消耗更多的动能．图4展示了撞击过程中流体的剪切速率(左)和黏度(右)随时间的变化．如图所示,随着液滴撞击倾斜液膜所带来的剪切效应,引发了不同位置处剪切速率的差异,进而导致液膜内相应位置的黏度呈现出不同的变化．

图4 剪切速率(左)和黏度(右)Fig. 4 Shear rates (left) and viscosities (right)

在液滴与液膜碰撞的初期(t*=0),液滴下落所夹带的空气使液膜受到了较大的剪切,这导致周围的剪切速率迅速升高,最大可达10 000 s-1．此时,虽然液滴未与液膜相混合,但液膜中的黏度已经出现明显降低的现象．此外可以发现,流体的剪切速率和黏度在中心点两侧也是不对称的,如图5(a)所示,相同距离内上游的黏度小于下游的黏度,并且此时下游黏度的作用范围更小．这是因为在重力作用下整个斜面上流动趋势是向下的,而液滴在上游的运动与之相反．相对运动会增大液滴对液膜的剪切作用,因此液膜在上游的黏度更低．研究发现,流体的剪切速率和黏度的作用是相互的,大剪切速率将导致低黏度,而高黏度则会抑制流体的剪切行为．随着时间的推移,液膜上游区域的液体速度会逐渐减小并趋于稳定,而下游区域仍然保持较快的扩散速度．在图4(t*=6.22)和图5(b)所示的撞击后期,由于除冰液的非Newton特性,上游黏度已经开始恢复,这表明上游的运动正趋于稳定,并且此时上游黏度大于下游黏度．由于液膜上游区域的黏度更高, 液体在运动过程中受到更大的阻力, 这将导致液膜上游区域的回落速度更快．我们进一步推测, 这种由非Newton特性引发的不同区域黏度的差异, 可能是导致液滴在撞击倾斜液膜后呈现出非对称运动特征的原因之一．

(a) t*=0.46 (b) t*=6.22

3.3 水滴撞击不同坡度的倾斜液膜

图6为水滴在不同坡度的倾斜液膜上的撞击过程,其中水滴的速度v=4 m·s-1,直径d=2 mm,Weber数We为408.3(模拟)和421.8,397.5,417.3(实验),除冰液液膜的初始浓度为0.5,液膜的厚度为0.5 mm．我们在实验中发现,液膜厚度受斜面坡度的影响．当坡度达到一定高度后,液膜下游的厚度略高于上游的厚度．由于实验手段的限制,并不能准确地探究坡度对非对称运动行为的影响．因此,选取了3个不同的坡度(水平、低、高)以验证数值模拟结果的准确性．从图中可以看到:水滴在撞击到水平液膜时,产生的液冠在中心点两侧为对称形状,并且产生的液冠较大;当水滴撞击倾斜液膜时,则呈现出明显的非对称特征,并随着坡度的增加而进一步增强．此外,随着坡度的增加,液冠在上游的生长明显受到抑制,表现为上游液冠半径减小,下游液冠半径增大的趋势．由3.1小节可知:受倾斜壁面的影响,液滴撞击液膜是一种非法向撞击行为,上游和下游的动量传递存在差异．随着坡度的增加,液滴下落速度v与斜面法线的夹角α将逐渐增大,进而造成沿斜面向下的切向速度vp增加．因此,当液滴在撞击高坡度的液膜时,液滴向下游传递的动量增加,从而促进了下游液冠的生长．这些结果揭示了坡度对液滴撞击液膜后的流体动力学行为有着重要影响．

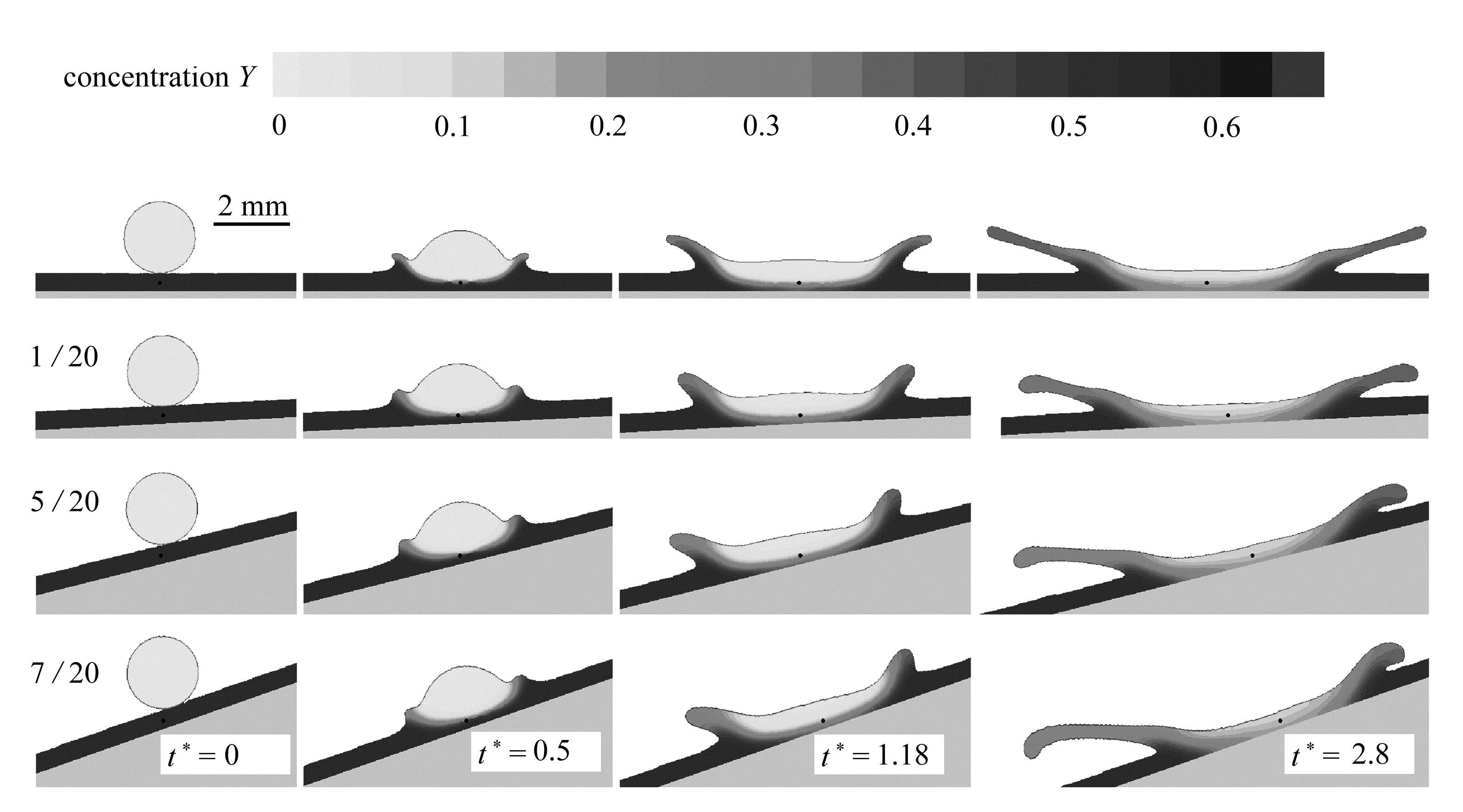
(a) 数值模拟结果(a) Simulation results

为了进一步分析液滴在不同坡度下撞击液膜后的动力学行为,我们得到了图7所示的液冠半径随时间变化的曲线．可以发现,随着时间的增加,液冠的上游半径Su和下游半径Sd逐渐增大．在撞击前期(t*=0～1.2),我们可以观察到不同坡度下的液冠半径大小近似相等．这表明,斜面的坡度并不会显著影响撞击瞬间的液冠生长情况,而是主要作用于撞击后流体的运动．根据图7(a)和7(b)的数据,我们可以发现,液滴在撞击液膜后形成的液冠上下游半径呈现出不同的规律．具体来说:在t*=2.5时,随着斜面坡度的增加,液冠上游半径Su逐渐减小,其中坡度为1/20的Su=4.1 mm,而坡度为7/20的Su=3.4 mm;相反,液冠下游半径Sd随着坡度的升高而增加,其中坡度为1/20的Sd=4 mm,而坡度为7/20的Sd=5 mm．说明斜面坡度对液冠上下游半径的影响存在显著差异,在上游部分,坡度的增加抑制了液冠持续生长的趋势;而在下游部分,则对液冠的生长产生了促进作用．

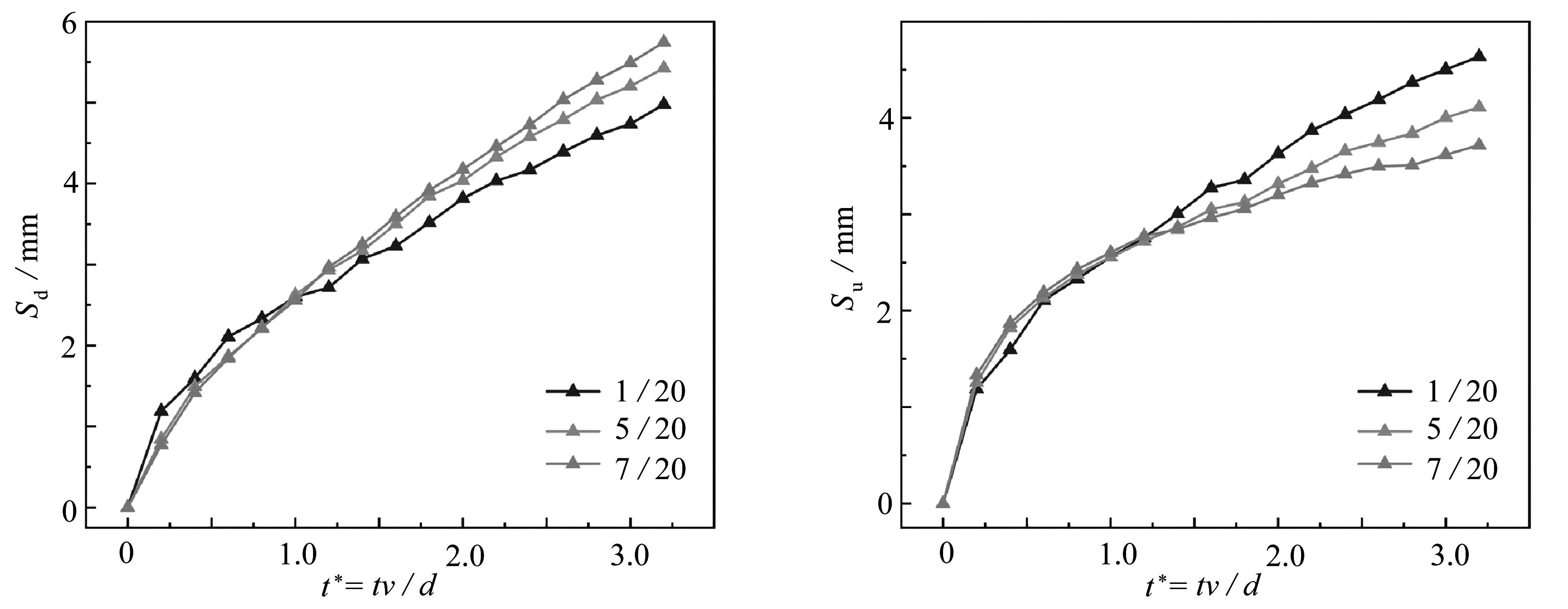
(a) 下游半径 (b) 上游半径(a) Downstream radii (b) Upstream radii

4 结 论

本文通过耦合相界面控制方程及组分输运方程建立了水滴撞击除冰液液膜的动力学行为模型,并通过实验结果验证进而修正了数值模型．在此基础上,分析了除冰液的非Newton特性和斜面坡度对撞击行为过程的影响机制,结果如下:

1) 水滴撞击倾斜除冰液液膜后,产生了非对称的液冠,并且撞击所带来的剪切效应引发了流体在不同位置处黏度的差异,这种由非Newton特性引发的不同区域黏度的变化,可能是导致液滴在撞击倾斜液膜后呈现出非对称运动特征的原因之一;

2) 液冠的外壁区域含有更高浓度的除冰液成分,这表明在液冠的形成过程中存在除冰液被带离液膜的情况,并且液滴内部的水分受流体运动的影响从撞击区域向液膜两侧扩散,在两者的耦合作用下液膜的黏度会进一步降低;

3) 随着斜面坡度的增加,液冠在上游的生长受到抑制,而下游液冠半径增大的趋势则更加明显,这表明高坡度减小了水滴对液膜上游的作用范围,加快了下游除冰液的脱离,随着水分在下游的积聚,导致液膜在下游的黏度大幅度降低．