多孔介质孔隙率对池沸腾传热性能影响机理的模拟研究*
何 树, 娄 钦
(1. 上海理工大学 能源与动力工程学院, 上海 200093;2. 上海理工大学 上海市动力工程多相流动与传热重点实验室, 上海 200093)
0 引 言
池沸腾作为一种高效的换热方式,已经被广泛应用于航空航天器、电子元器件以及电厂等各个领域.对于沸腾换热过程来说,CHF、换热系数以及初始壁面过热度等指标是衡量沸腾换热性能好坏的关键,因此如何提高CHF、有效降低初始壁面过热度,增大换热系数,对优化沸腾换热性能至关重要.近几十年来,为了提高沸腾换热性能,学者们采取了各种措施,包括对加热器表面结构改造[1-2],在工作流体中添加活性剂[3]以及在加热器表面施加磁场或者电场进行强化[4]等.多孔介质因具有较大的换热表面积[5]、较高的有效导热系数[6]等优势,成为相变传热领域最具发展前景的冷却技术之一,一些学者采用多种方法研究了多孔材料在不同条件下改善沸腾换热的潜力.
作为人们认识复杂物理现象的重要方法,实验方法被用于含有多孔介质的池沸腾换热问题的研究.El-Genk和Parker[7]采用实验方法研究了HFE-7100介质液体在数十至数百微米孔径的多孔石墨中的沸腾过程,并与相同尺寸的光滑铜进行了对比.他们发现在沸腾开始之前,由多孔石墨释放的微小气泡增强了自然对流换热,同时,多孔石墨的存在增加了成核点位,强化了初始核态沸腾.同样采用实验方法,Chi等[8]研究了去离子水在更小直径(孔径大小为50~70 nm)多孔介质中的池沸腾换热.他们发现,纳米多孔表面的初始壁面过热度比非涂层的表面要小,而且纳米多孔涂层表面的核态沸腾换热速率比未涂层的表面大.相似地,还有一些学者也发现了不论是微米级孔径还是纳米级孔径,多孔介质的存在都能够有效地降低初始壁面过热度,从而强化沸腾换热[9-13].此外,也有一些学者发现,一些特殊的孔隙结构也可以提高沸腾换热性能.Mori和Okuyama[14]采用实验方法研究了饱和水在多孔蜂窝结构板上的池沸腾过程,发现多孔蜂窝板的毛细作用实现了自动供液,蜂窝状结构使液汽分离,降低了蒸汽逸出的流动阻力,最终使CHF增大至2.5 MW/m2,约为普通表面的2.5倍.另一方面,Yuki等[15]用实验研究了莲花型多孔铜板中饱和水的沸腾传热性能,他们发现采用莲花铜板加热表面,CHF可以增加到216 W/cm2,几乎是光滑表面情况下的两倍.尽管Mori等[14]和Yuki等[15]采用的孔隙结构不同,但这些孔隙结构提高CHF的原理都在于增强毛细作用下的自动供液能力,增加有效成核点位以及增大传热面积.此外,还有学者探究了多孔介质的结构参数对池沸腾换热的影响,Ji等[16]研究了非均匀和均匀多孔涂层表面的池沸腾传热,他们的研究结果表明,周期性地改变颗粒基底厚度的多孔涂层表面可以提供更高的CHF值(最大可达到普通表面的3.7倍).An等[17]研究了多孔材料的导热率和表面润湿性对沸腾换热的影响,发现多孔材料导热率对沸腾传热的影响比润湿性的影响更大.
除了实验方面,一些学者对多孔介质在不同工作流体中的沸腾过程进行了数值模拟研究.Li和Leong[18]基于两相混合模型对泡沫铝在水中的流动沸腾过程进行了数值模拟,发现在沸腾过程中,气泡通常成核于金属泡沫韧带和加热器表面接触的角点处,同时也得到了该过程的沸腾曲线,其数值结果与他们的实验结果吻合较好.Peralta等[19]对分离相模型进行了改进,研究了多孔介质中冷却剂的相变,同时考虑了液相区和气相区的对流效应.前期的大多数模拟工作采用的是体积平均法.而近年来,在众多数值方法中,格子Boltzmann(LB)方法[20]这种介观方法在两相流建模方面表现出了巨大的潜力,特别是对于界面复杂的拓扑变化(如气泡变形、聚结、破裂等)或复杂几何形状[21]的实现等,可以认为是孔隙尺度建模的良好方法[22-25].而在多孔介质沸腾领域,Mondal等[26]采用LB方法研究了方形截面实心柱阵列内池沸换热的增强作用.其结果表明,多孔阵列的存在使得受热面在较早的时间步长上有更多的成核位点,从而增加了热流密度(CHF值约为平板表面的1.36倍),除此之外,他们对比了两种高孔隙率(98%,90%)的多孔阵列后发现,孔隙率对传热速率的敏感性显著,在表面过热度较高时尤为明显,并预测了存在最佳孔隙率,但并没有对最佳孔隙率进行量化研究.Shi等[27]采用多松弛LB方法模拟了亲水金属泡沫表面的池沸腾传热过程,研究了金属泡沫的孔隙率对沸腾传热的影响,但其研究的孔隙率仅限在89.3%~97.3%范围内,并没有考虑更小的孔隙率,且没有得到最优的孔隙率结果.除了对孔隙率进行研究之外,Qin等[28]也采用LB方法模拟了一种二维多孔结构在水中的沸腾传热过程,在孔隙率一定的情况下得到了泡沫厚度对沸腾传热的影响.
以上研究表明,多孔介质对于池沸腾换热的强化作用显著.但由于其内部存在特殊的拓扑结构,因此,在沸腾过程中多孔介质孔隙内的气泡动态行为十分复杂,而目前对于该过程的数值研究仍较少,且对池沸腾换热的影响机理研究尚待完备,对于多孔介质孔隙率的研究还缺乏一些具体的影响机理以及定量的分析.因此,有必要对多孔介质的池沸腾过程及其孔隙率的影响机理进行更详细的孔隙尺度研究.基于此,本文构造了一种二维均匀排列的多孔介质,采用伪势LB模型在孔隙尺度下模拟了多孔介质的池沸腾过程,详细分析了不同过热度下,高、中、低孔隙率的多孔介质中气泡的动力学行为特性,并对沸腾过程中典型的气泡状态进行了力平衡分析,最后深入探究了多孔介质的孔隙率对沸腾换热曲线的影响.
1 相变LB模型
在LB模型[29]中,流体密度的分布函数演化方程为
(1)
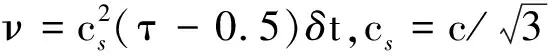
(2)
其中wi是权重系数,在D2Q9模型中速度的9个方向由下式给出:
(3)
权重系数分别为w0=4/9;wi=1/9,i=1,2,3,4;wi=1/36,i=5,6,7,8.在方程(1)中,力项Fi由下式给出:
(4)
其中Δu=Fδt/ρ为由合力F计算出的速度,合力F定义为
F=Fint+Fext+Fs,
(5)
其中Fint为粒子间的相互作用力,Fext为合外力, 一般为重力或者浮力,Fs为表征流体与固体壁面润湿性的力.Fint定义为
(6)
Fs定义为
(7)

(8)

Fext(x)=g(ρ(x)-ρave),
(9)
g为重力加速度,ρave为每个计算步下整个计算域的平均密度.温度的演化方程为[29]
(10)

(11)
其中U为宏观速度.式(10)中的源项φ由下式给出:

(12)
cv为比热容.相关宏观量的计算如下:
(13)
(14)
(15)
(16)
由于固体加热器以及多孔介质与流体的热物性不同,导致流固交界面温度变化不连续.为了避免这种不连续性,采用Li等[31]提出的二阶精确共轭传热边界条件.在该方法中,沿格子速度方向指向流体的加热器或者多孔介质xs,以及沿格子速度方向指向固体的加热器或者多孔介质周围的流体节点xf的温度分布函数分别设为
(17)
(18)

(19)
其中ρl和ρv分别为饱和液体和饱和蒸汽的密度.
2 物理模型和计算参数
由于均匀多孔介质结构内部流体输运机理更容易刻画,同时也因为随着3D打印技术的发展,越来越多的学者将规则多孔结构应用在沸腾过程中以达到强化换热的目的[32-34].因此,本文设计了一种简化的均匀二维排列的多孔介质进行研究,不仅可以便于分析多孔介质内的沸腾换热机理,也可以更方便地推广到实际应用中.多孔介质池沸腾的模拟实验如图1(a)所示,整个计算区域设置为Lx×Ly=300×600(格子单位),其中红色部分为加热器,高H=50,长LH=200,加热器上方放置均匀多孔介质.初始时,计算区域内充满温度为Tsat=0.9Tc,密度为ρl的静止饱和液体.下边界(y=0)的流体部分采用绝热无滑移边界条件,计算域的两侧为周期边界条件,计算域顶部边界为对流边界条件[35].加热器底部加热方式采用等温加热,其加热温度为Tb,加热器的左右边界采用绝热无滑移边界条件,加热器上方速度无滑移,温度分布采用流固耦合边界条件[31].多孔介质内y方向相邻两层多孔介质块之间的传热方式为导热,其处理方式如图1(b)所示.如图1(b)所示的任意两个在y方向相邻的多孔介质块,其中A、B、C、D示意部分分别是下方多孔介质临近流体侧的固体部分、上方多孔介质临近流体侧的固体部分、最靠近下方多孔介质的流体层,以及最靠近上方多孔介质的流体层.为了实现多孔介质之间的导热,将下方多孔介质A层固体格点的温度分布赋值给上方多孔介质下最临近的流体格点D层;同时将上方多孔介质B层固体格点的温度分布赋值给C层流体格点.除此之外,C层和D层流体格点将与其周围的流体格点保持绝热(即流体中画叉的部分与周围画圆的部分保持绝热),而多孔介质则分别与C层和D层流体进行耦合传热,最终实现多孔介质间的连续热传导[28].

(a) 物理问题示意图 (b) 多孔介质间的导热示意图 (a) Schematic diagram of physical problems (b) Schematic diagram of heat conduction between porous media
本文中所采用的模拟参数如下:a=2/49,b=2/21,R=1.0,Tc=0.196 1,Tsat=0.9Tc,ρl=5.426,ρv=0.811 3,σ=0.009 5.加热器与多孔介质内部初始温度设置为0.9Tc,重力加速度g取(0,-0.000 08),比热容cp,l=cv,l=4.0,cp,v=cv,v=2.0,动力黏度μl=0.325 7,μv=0.048 7,热扩散系数αl=0.05,αv=0.06,加热台的热物性参数取为(ρcp)s=21.704,αs=1.5,λs=32.556,而多孔介质的热物性参数取为(ρcp)s=21.704,其中,αs根据其有效导热率的变化而变化.
下文中所采用的量均为无量纲量,其对应的特征长度、特征速度以及特征时间如下:
(20)
则对应的无量纲长度以及无量纲时间为L*=L/l0,t*=t/t0.本文所用的固体材料为铜,流体为FC-72,模拟工况设计和参数的选取是依据实际固体和流体的性质,相关参数格子单位与物理单位的转换关系详见表1.无量纲壁面过热度Ja以及加热器底部(y=0)的局部温度梯度ΔyT|x,0计算如下:

表1 格子单位与物理单位转换
(21)
其中hfg为流体的潜热,本模拟中取hfg=0.624,δy为格子空间步长.无量纲空间平均热流密度q计算如下:
(22)
无量纲时间-空间平均热流定义为

(23)
3 模 拟 结 果
3.1 不同过热度下多孔介质中气泡的动力学行为
本小节研究了不同过热度下气泡在多孔介质中的成核、 生长、 滑动、 上升、 到达顶部以及逸出多孔介质等动态特性.为了对比气泡行为在不同沸腾模态下的差异, 我们模拟了加热温度分别为0.98Tc, 1.01Tc以及1.05Tc的沸腾过程, 研究对象为3个不同孔隙率的多孔介质, 它们的孔隙率分别为92.6%, 73.2%以及61.2%,除孔隙率外,它们的其余参数设置均相同,具体为孔隙密度PPPI=351,高度h*=7.25,有效导热率λeff=32.556,表面接触角设置为57°.
图2为ε=92.6%的多孔介质在3种加热温度下,池沸腾过程中气泡的运动状态图,其中图2(a)、2(b)和2(c)的加热温度分别为0.98Tc,1.01Tc以及1.05Tc.从图2(a)中可以发现:在t*=33.50时刻,加热面中心有两个气泡成核.随着沸腾的持续进行,这两个气泡逐渐生长,在t*=60.29时刻,由于多孔介质的阻碍发生形变(如图中的红色虚线框所示),随后两个气泡在浮力的作用下脱离加热器表面,此时加热器表面残余了两个气泡.初始的两个气泡在t*=69.23时刻穿过多孔介质顶部并逸出,上一时刻残余在加热器表面的气泡则开始生长,随后会参与下一阶段的气泡逸出循环过程,显然此时为典型的核态沸腾状态.如图2(b)所示,随着加热温度提高到1.01Tc,可以发现:多孔介质中气泡的成核位置明显增加,成核时间也随之提前,在t*=8.93时刻,加热器上表面的4个间隔内均有气泡生成.随着气泡的生长,它们遇到了多孔介质的阻碍,这与低过热度的情况一致, 但不同的是, 由于过热度的增加, 相变更加剧烈, 生成的气泡质量明显增加(t*=33.50).随后,这些气泡在浮力的作用下向上升,并到达多孔介质顶部,两侧的气泡率先逸出(t*=40.20),中心的气泡则在t*=44.66时刻才与下方的气泡分离,并且在分离的过程中由于接触线的拉长,会产生一些小气泡随之分离.继续增大加热温度至1.05Tc,从图2(c)中可以发现:由于底部加热温度的增加,成核时间进一步提前(t*=6.70),而在第一轮相变产生的初始气泡逸出后(t*=26.80),新一轮的气泡聚集在加热器上表面,形成了一层气膜(t*=35.73),显然此时已到达稳定膜态沸腾状态.

(a) Tb=0.98Tc
如图3所示,当多孔介质的孔隙率减小至73.2%时,不同过热度下的气泡状态也发生了变化.图3(a)的加热温度为0.98Tc,可以发现:在此加热温度下,气泡的成核和脱离状态与ε=92.6%的多孔介质大致相同,均有两个气泡在中心成核,随后在生长过程中受到多孔介质的阻碍,最后在浮力的作用下逸出多孔介质.但有所不同的是,ε=73.2%的多孔介质其气泡成核时间略晚(t*=40.20),分别统计了ε=92.6%和ε=73.2%多孔介质内的气泡从成核到与加热器表面脱离的时间段内生成的气泡质量(即图2(a)中的t*=33.50至t*=66.99时刻和图3(a)中的t*=40.20至t*=73.69时刻),发现在相同时间内(Δt=33.49),ε=73.2%的气泡增加了4 140(格子单位),而ε=92.6%的气泡只增加了3 034(格子单位),这说明孔隙率的减小虽然会使气泡成核时间相对延后,但沸腾的相变速率却会增大.这与Shi等[27]的研究结果一致,他们发现孔隙率越小,气泡越容易合并,骨架对气泡离开的阻碍作用越强,且在孔隙率较小的金属泡沫中,蒸汽成核体积较大,相变速率增加,这是传热面积增大和气泡释放阻力增大的相互作用结果.如图3(b)和3(c)所示,继续增加加热温度至1.01Tc和1.05Tc.由图3(b)可以发现:壁面过热度的增加使气泡成核点明显增加,气泡质量也随之增大,但成核与脱离的时间与ε=92.6%的多孔介质相比略晚(t*=11.17和t*=58.06).而当加热温度提升至1.05Tc后,如图3(c)的后3幅图所示:在图中的红色虚线框内,气泡脱离之后加热器表面仍然会残余一层气膜,这说明在此过热度下沸腾同样达到了膜态.

(a) Tb=0.98Tc
如图4所示,进一步减小孔隙率至ε=61.2%.由图4(a)可以发现,在加热温度为0.98Tc时,成核时间也相对延后(t*=58.06),同时可以发现生成的气泡在生长过程中更容易聚集在一起(t*=91.56),且气泡在t*=102.72脱离时尾迹会拖得更长.我们同样统计了气泡从成核到与加热器表面脱离的时间段内生成的气泡质量(即图4(a)中的t*=58.06至t*=91.56时刻,Δt=33.50),发现气泡质量增加了4 330(格子单位),与ε=73.2%的多孔介质相比又有所增加.由图4(b)可以发现:提高加热温度至1.01Tc后,气泡在生长过程中很容易在加热台表面聚集形成一层气膜(t*=49.13),且在气泡脱离后残余的气泡仍然会聚集在一起,这应该是由于孔隙直径过小导致的,而这种气泡状态也必然会恶化沸腾传热.继续提高加热温度至1.05Tc,如图4(c)所示:随着壁面过热度的增加,气泡的聚集行为更加明显(t*=51.36),且此时的气泡阻力过大,不易脱离(t*=73.69).

(a) Tb=0.98Tc
以上研究完整地展现了含多孔介质的加热器的池沸腾从初始核态到完全模态的过程.除此之外,对比3种孔隙率多孔介质的沸腾过程后发现:减小多孔介质的孔隙率能够有效地增加沸腾的相变速率,强化沸腾换热;然而,气泡的成核时间会相对延后,并且减小孔隙率还会使气泡更易聚集,形成气膜,气泡上升阻力会增大,其逸出多孔介质的速率也会随之降低.需要注意的是,从3个沸腾状态的图中均会发现气泡成核于多孔介质间隔内.而这与Li等[18]所得到的,气泡通常成核于金属泡沫韧带紧密附着在加热器表面的节点处的结论略有不同,这是因为气泡成核的位置受多孔介质的结构参数(如孔隙密度、有效导热率以及表面润湿性等)影响[17],我们发现:在一些参数下,气泡成核发生在方肋格子角点处;而在另一些情况下,气泡会成核在方肋格子之间.如对于本文所研究的工况,当接触角为73°,孔隙率为61.2%,加热温度为1.01Tc时,气泡首先在方肋格子角点处成核(如图5所示);而本文中图2—4对应的参数,此时是在方肋格子之间成核,这一结论与Liu等[36]的模拟结果一致.

图5 孔隙率为61.2%、接触角为73°的多孔介质在加热温度Tb=1.01Tc下的气泡状态图Fig. 5 Bubble state diagrams of porous media with a porosity of 61.2% and a contact angle of 73° under heating temperature Tb=1.01Tc
3.2 沸腾过程中单气泡在多孔介质中的力平衡
本小节对沸腾过程中单气泡在多孔介质中的运动行为进行了力平衡分析.根据上一小节的分析,由于多孔介质的存在,气泡的运动行为主要包含成核与穿过多孔介质这两种情况,这两种典型的气泡状态显示在图6中(其中浅蓝色形状代表气泡,红色方格代表二维多孔介质骨架,剩余的箭头代表沸腾过程中作用于气泡上的力).总体来说,如图6(a)所示,沸腾过程中作用于气泡成核生长的力一般包括重力Fg、浮力Fb、蒸发动量力Fm[37]、接触压力Fcp以及表面张力Fσ.除此之外,如图6(b)所示,当气泡通过多孔介质时,由于气泡在多孔介质表面滑动,故它们之间会产生摩擦阻力Ff[38].因此,池沸腾过程中多孔介质内的气泡在x方向和y方向的力平衡方程可由如下两式表示:

(a) 单气泡成核生长 (b) 单气泡穿过多孔介质(a) The single bubble nucleation growth (b) The single bubble passing the porous medium
∑Fx=Fσx+Fcpx+Ffx+Fgx+Fmx=0,
(24)
∑Fy=Fσy+Fcpy+Ffy+Fgy+Fmy+Fb=0.
(25)
表面张力Fσ的定义为[38]
Fσ=πdaσsinθ,
(26)
其中da为气泡的接触直径,σ为表面张力系数,θ为气泡与固体的接触角.接触压力Fcp定义为[39]
(27)
其中Rr为气泡的等效半径,接触压力的方向垂直于接触壁面,接触直径da可由下式计算:
(28)
其中lr为气泡的基线周长.蒸发动量力Fm定义为[37]
(29)
其中qe为蒸发热流密度,hlv为界面处的蒸发潜热,As为界面面积.当气泡的受力情况满足式(24)和(25)时,气泡在当前位置成核生长,直至气泡体积达到一定大小时,浮力增大,y方向上的平衡被打破,气泡脱离加热面.气泡继续上升后会遇到多孔介质的阻碍,如图6(b)所示,此时影响气泡上升的阻力主要为气泡与多孔介质间的接触压力Fcp与摩擦力Ff.摩擦力定义为Ff=μFcp,其中μ为摩擦因子,摩擦力的定义参考前人的研究[40-41],此外,根据Karakashev等[42]的研究,摩擦因数μ的大小和气泡与固体壁面间微小流体层的厚度相关,而该厚度则与工作流体的黏度、表面张力以及气泡的运动速度相关.因此,接触压力的大小在很大程度上影响着气泡上升的速度,这与Huang等[38]的实验研究中对接触压力的观点一致.
3.3 孔隙率对多孔介质池沸腾曲线的影响
本小节研究了孔隙率对多孔介质池沸腾换热曲线的影响.根据3.1小节的研究,继续设置另外4个不同孔隙率的样本进行对比研究,总共7个样本,它们的孔隙率由高到低分别设置为ε=97.7%, 92.6%, 85.2%, 73.2%, 67.6%,61.2%,53.5%.其余参数与3.1小节一致.
图7为不同孔隙率下的多孔介质样本以及不含多孔介质的光滑平板的沸腾曲线.从图中可以观察到众多孔介质样本的沸腾曲线均在光滑平板曲线的左上方,这说明加上多孔介质之后,既相当程度地提高了CHF值(平均提高了约3.2倍),也降低了成核的初始壁面过热度(降低了约18.2%),显著增强了沸腾换热.而这一结果也与Vemuri和Kim[43]的实验结果一致,他们对厚度为70 μm的氧化铝纳米多孔表面在饱和FC-72介质液中的池沸腾换热进行了实验研究,发现纳米多孔表面比普通表面的初始壁面过热度降低了30%.他们将引起这个现象的原因归结为纳米多孔结构的存在增加了蒸汽体积和活性成核点密度,从而增强了沸腾换热性能.

图7 不同孔隙率的多孔介质以及光滑平板的沸腾曲线Fig. 7 Boiling curves of porous media with different porosities and smooth plates
从图7中还可以发现:当孔隙率从97.7%开始减小直至ε=73.2%时,沸腾换热曲线随之向左上方移动.我们随机选取了ε≥73.2%的4个样本在核态沸腾区域的气泡脱离状态进行分析.图8显示了不同孔隙率的多孔介质样本在加热温度为0.99Tc,t*=51.36时刻的气泡状态以及其所对应的温度场(该图所显示的气泡均为第一次相变成核的气泡脱离情况).由图7可以发现:ε=97.7%和ε=92.6%的两个样本其气泡脱离较快,而随着孔隙率降低到85.2%和73.2%,气泡脱离速度逐渐变慢,这与3.1小节所观察到的现象一致,这是由于孔隙率的减小增大了气泡的脱离阻力.与此同时,观察同一时刻下对应的加热器内部的温度分布却发现:大孔隙率的多孔介质内气泡虽然脱离较快,但是其加热器内部的温度场分布却不如小孔隙率的样本分布均匀,且其上表面(与多孔介质相接触的那一层表面)温度较高;而随着孔隙率的降低,加热器内部的温度场分布愈加趋于均匀,其上表面的温度亦随之降低.这是因为随着孔隙率的降低,换热面积随之增大,热量能够更快地传导.由此可见,在本研究中,当孔隙率ε≥73.2%时,随着孔隙率减小,换热面积增大,与此同时,气泡自由上升阻力也随之增大,但此时增大的阻力并不足以让气泡聚集在加热面上形成气膜,对沸腾传热的恶化作用有限.因此当孔隙率ε≥73.2%时,由于减小孔隙率而增大换热表面积的强化传热作用大于增加气泡上升阻力的恶化传热作用.在Xu等[44]的金属泡沫表面池沸腾换热与槽阵泡沫表面气泡团簇生长行为的实验中同样发现,在孔密度一定的情况下,孔隙率的大小影响着气泡与金属泡沫间的传热面积以及气泡的上升阻力,从而影响沸腾传热性能,这三者之间存在相互耦合的关系,这与本文的结论一致.

(a) ε=97.7%(b) ε=92.6%
如图7所示,当ε=73.2%时,继续减小孔隙率却发现沸腾传热发生了恶化.为了进一步分析其原因,随机选取了两个加热温度下的某两个时刻,对比分析了ε=73.2%和ε=67.6%两个样本的气泡状态.图9显示了这两个样本在同一加热温度下的气泡行为.横向对比图9(a)和9(b)可以发现:当加热温度Tb=1.00Tc时,分别在t*=51.36和t*=91.56这两个时刻下,ε=67.6%样本沸腾过程中的气泡均聚集在一起,在加热器表面形成了一层气膜(如图中的红色虚线框所示);而当加热温度增加至Tb=1.04Tc时,在t*=33.50以及t*=53.60这两个时刻,ε=67.6%样本的气泡也聚集在了一起.

(a) ε=73.2%,Tb=1.00Tc
反观图9(a)和9(c),ε=73.2%的样本在同一时刻下则并没有聚集形成气膜.通过随机选择的两个加热温度分析发现:ε=67.6%的样本与ε=73.2%的样本相比,在沸腾过程中其气泡都更容易聚合在一起,除此之外,我们在ε=61.2%和ε=53.5%这两个样本中也观察到同样的现象,3.1小节已经对ε=61.2%的样本进行了研究,而对于ε=53.5%的样本这里也不再赘述.以上研究表明:多孔介质的孔隙率存在一个临界最优值,即ε=73.2%,使得沸腾传热性能达到最优,一些学者也通过实验研究得到了多孔介质的孔隙率过高或者过低都不利于沸腾换热性能提高的结论.如Li等[45]用实验研究了水平导电微孔包覆表面池沸腾过程,发现多孔涂层的孔隙率过高或者过低都不利于提高CHF值;Ou等[46]用实验对烧结铝粉芯多孔介质内的池沸腾换热性能进行了研究,同样发现烧结多孔芯的孔隙率过大或者过小都不利于传热.
此外,如图10所示,我们将模拟所得到的不同孔隙率的CHF结果与Mori等[14]的理论预测结果进行了对比.可以明显看出,Mori等的理论预测结果与本文的模拟结果趋势一致,即存在一个最佳孔隙率使得CHF值达到最优.当然,从图中还可发现,本文的计算结果与Mori等的预测结果存在一定的差异,这是因为多孔介质内部的结构以及流体或固体的物理性质(如黏度、表面润湿性、导热系数等)所造成的.
为了探究孔隙率小于73.2%的样本内的气泡更容易聚集的原因,以ε=67.6%的样本为例对其气泡上升阻力进行了分析.如图11(a)所示:加热温度Tb=1.00Tc,在t*=46.90时,正中的两个气泡其自由生长遇到了多孔介质的阻碍, 未能及时地脱离, 而随着体积的不断增大, 蒸发动量力Fm的横向x分量使得气泡横向扩张.与此同时,由于中心气泡的生长引起了流场的扰动,两侧气泡在流场的扰动作用以及Fm的横向x分量的共同作用下也向中心聚合,总体的运动结果如图11(b)所示,在时间到达t*=53.60时,这4个气泡聚集在加热面上形成一层气膜.

(a) 气泡聚集 (b) 形成气膜(a) Bubble aggregation (b) Gas film formation
表2统计了7个孔隙率样本的最大接触压力大小Fcpm以及气泡脱离多孔介质前的平均上升速度Vave.可以发现:由于孔隙率的降低,在固定高度以及孔隙密度的情况下,小孔隙率的多孔介质其孔隙直径会随之减小,气泡的接触压力项Fcp中的当量半径Rr变化不大,而气泡的接触直径da却随之增大.根据式(27)可知,最终导致气泡的接触压力Fcp增加,气泡上升阻力增大,上升速度随之降低.在Huang等[38]所做的,关于水和庚醇溶液在池沸条件下的梯度金属泡沫池沸传热性能的实验研究中也发现,金属泡沫的孔隙减小,有限的空间会阻碍气泡的膨胀与上升.

表2 不同孔隙率的多孔介质样本其气泡最大接触压力Fcpm以及平均上升速度Vave(格子单位)
根据本节的研究可以发现:在其余参数设置均相同的情况下,随着孔隙率的减小,换热面积也会增大,但孔径会减小,气泡脱离阻力会逐渐增大,且当多孔介质的孔隙率减小到一定程度后,阻力过大,气泡难以逸出多孔介质,而更多的气泡在受到阻碍后会聚集在一起,最终形成一层气膜覆盖在加热器表面,导致周围的液体不能及时的补充,使沸腾换热恶化.
4 结 论
本文采用LB方法研究了均匀多孔介质的孔隙率对池沸腾传热性能的影响.首先,以孔隙率ε=92.6%,73.2%,61.2%的均匀多孔介质为例分析了其在不同过热度下的气泡运动行为,并对气泡成核和受到多孔介质阻碍这两种典型状态进行了力平衡分析.研究发现:减小孔隙率能够增大相变速率,但同时也会增大气泡脱离阻力,使气泡易聚集成气膜,并延后成核与脱离的时间.随后,详细研究了不同孔隙率对池沸腾换热性能的影响机理,重点分析了沸腾过程中的气泡行为,并给出了不同孔隙率下池沸腾从核态沸腾到模态沸腾的热流密度曲线,并且将模拟结果与相关沸腾实验进行了印证.研究发现:虽然多孔介质能够增强流体的扰动,增加换热面积与成核点位,强化导热,且能够降低壁面的初始过热度(平均约18.2%)并显著提高CHF值(平均3.2倍),但是其提升的性能大小与多孔材料的孔隙率有关,具体研究结论如下:
1) 有多孔介质存在可以降低气泡成核的初始壁面过热度,并提高CHF.与平板相比,有多孔介质存在时气泡成核的初始壁面过热度降低了18.2%,同时CHF最大可提高3.6倍.
2) 当多孔介质的孔隙率ε≥73.2%时,减小孔隙率能够增大换热面积,增加相变速率,降低初始壁面过热度,从而强化沸腾换热.
3) 当ε<73.2%时,由于过小的孔隙增加了沸腾过程的气泡逸出多孔介质的阻力,延长了气泡在多孔介质内的停留时间,最终在流场与蒸发动量力Fm的共同作用下,多个气泡更易聚集在加热器表面形成气膜,这不利于沸腾换热的持续进行,最终导致沸腾传热恶化.
4) 通过与多孔介质内的气泡受力分析发现当孔隙率过小时,气泡的接触压力Fcp逐渐增大,导致气泡上升阻力增大,最终使得气泡上升速度降低.
本文的研究结果表明:多孔介质对于池沸腾换热的强化作用显著,但其孔隙率存在最优值,使得沸腾换热性能提升最大,在实际实验或者应用过程中,针对固定的结构参数,仅改变多孔介质的孔隙率的情况下,可以优先在高过热度下对孔隙率由低到高的多孔介质进行沸腾传热实验测试,若观察到沸腾过程中的气泡从易聚集状态变为自由脱离状态时,即可确定该结构的最佳孔隙率范围.

