基于时空最优低维动力系统的多尺度可压缩湍流数值模拟方法*

齐 进, 吴锤结

(1. 北京应用物理与计算数学研究所, 北京 100088;2. 大连理工大学 力学与航空航天学院, 辽宁 大连 116024)

1 Professor ZHOU Peiyuan’s Pioneering Contribution to Turbulence Research and the Basic Idea of the LMS Method

1.1 ZHOU Peiyuan’s Pioneering Contribution to Turbulence Research

Professor ZHOU Peiyuan, the father of computational modeling[1], published a groundbreaking paper[2]on turbulence modeling in Chinese Journal of Physics in 1940, in which he proposed that to study the numerical simulation of turbulence, it is necessary to analyze and solve the fluctuating velocity field. He first presented the 2nd- and 3rd-order velocity correlation equations. Then, he transformed the 4th-order correlation function into a closure equation by summing the product of 2 2nd-order correlation functions. This process is the foundation of the turbulence modeling theory. However, it is not the best method for computationally modeling turbulence (see section 4).

1.2 Basic Ideas of the LMS Method

In this report, for clarity, we presented the term “small-scale” as “SGS-scale” in the LES method, and in the LMS method (see section 2), the “SGS-scale” includes “middle-scale” and “small-scale”.

Under Zhou’s idea, based on the first principles, with the box filtering and without the Favre filter and any artificial assumption, coupled with the LES equation, a set of spatiotemporal multiscale optimal low-dimensional dynamical system equations were solved with a small-scale turbulent model to obtain the middle-scale flow field, together with the LES large-scale averaged flow field to obtain a new kind of approximate solution of turbulence.

In this report, several problems encountered in the research and their solutions were studied first, as are shown in section 2 to section 5. Then, the LMS method was established systematically in section 6, and its application to the re-shock Richtmyer-Meshkov problem was discussed in section 6.3. Finally, concluding remarks were given in section 7.

2 Classification of the Numerical Simulation Methods for

Turbulence and Basic Features of the LMS Method

2.1 Classification of Numerical Simulation Methods for Turbulenc e F rom the Point View of Scale Decomposition

Traditional numerical simulation methods for turbulence include RANS[3], LES[4], DES[5]and DNS[6]. We classified these methods from the point view of scale decomposition.

1) Class L(large): all scales of turbulence are solved with CFD methods to obtain a unified solution of turbulencef, such as DNS.

2) Class LS(large-small): the turbulence flow field is decomposed into large-scale and SGS-scale fields. The large-scale equation is solved with the CFD method, and the SGS-scale equation can be solved by:

① Coupling the solution of the CFD method with the large-scale equation;

② Coupling the dynamic system or optimal low-dimensional dynamic system method with the large-scale equation;

③ Using the SGS model in the LES equation.

(1)

Since the SGS-scale in Class LS includes a wavenumber range with completely different turbulence characteristics, it is not easy to find accurate turbulence models in RANS, LES and DES.

Fig. 1 Basic characteristics of turbulence

3) Class LMS(large-middle-small): it can be seen from fig. 1 that for high Reynolds number turbulence, the Kolmogorov spectra can be divided into the energy-containing range and the universal equilibrium range, in which the inertial sub-range is dominated by convection and dissipation is very small. Moreover, in the dissipation range most turbulent energy is dissipated. Therefore, according to the basic characteristics of turbulence, the whole range of the turbulence spectrum wavenumbers can be divided into 3 parts with completely different characteristics, i.e., the energy-containing range, the inertial subrange and the dissipation range.

(2)

Class LMS includes the LMS(low-dimensional dynamical systems multiscale simulation) method (see section 6).

2.2 Basic Features of the LMS Method

The middle-scale quantitiesf′ reflect the convection characteristics of the anisotropic inertial subrange, which is obtained by coupling the spatiotemporal optimal low-dimensional dynamical system equation. This equation includes large- and middle-scale quantities, with the large-scale equation in the middle-scale grid Δx/2p,p≥1.

Since the dissipation range contains most of the dissipation effects of turbulence, the small-scale quantities are very small and isotropic, and the grid sizes in the dissipation range are very small, it is not suitable for direct solving. The effects of small-scale quantitiesf″ are found by a small-scale SGS turbulence model expressed with the middle-scale quantities, the middle-scale deformation tensor and the large-scale stress tensor, which provides an appropriate dissipation effect.

3 Average and Filtering Operations and Calculation of Spatial Correlation of Box Filtering

In this section, we clarified the concepts of average and filtering operations and the correlation operation related to the box filter used in the LMS method.

3.1 Average and Filtering Operation

The following are the definitions of RANS and LES, in which the key concepts are the averaging operations (RANS) and filtering operations (LES).

RANS: by using turbulence averaging operations (including the time average, spatial average, ensemble average, etc.), the flow variables are decomposed into mean and fluctuating quantities;

LES: by using turbulence filtering operations (including the box filter, the Fourier filter, the Gaussian filter, etc.), the flow variables are decomposed into large-scale quantities and SGS-scale quantities.

3.1.1 The Filtering Method

(3)

3.1.2 The Box Filter

The filtering function of the box filter for the grid scale Δxiis

(4)

As is shown in fig. 2, the box filter is the volume average on the grid centered aroundx.In RANS, the grid space averaging is equivalent to the box filtering. Therefore, only the RANS and LES in DES use grid space averaging, then, the DES is determined to be conceptually correct. Since generally, the averaging (RANS) and the filter (LES) used in the DES method are not compatible with each other, therefore the DES method is conceptually wrong, even though sometimes good results of turbulence numerical simulation can be obtained.

3.2 Variable Correlation, Spatiotemporal Correlation and Calculation o f S patial Correlation of the Box Filtering

3.2.1 Variable Correlation

Correlation function: the average or filter of the self-multiplication of the same or different fluctuating or SGS-scale quantities is generally not equal to zero, and their values are related to the degree of correlation between these 2 fluctuating or SGS-scale quantities.

(5)

Correlation coefficient: using the correlation coefficientRto measure the degree of correlation betweena′ andb′ yields:

(6)

IfR=±1, then they are completely correlated. It can be seen that each fluctuating or SGS-scale quantity is completely related to itself.

3.2.2 Spatiotemporal Correlation and Calculation of the Spatial Correlation of the Box Filtering

Since we didn’t use time-averaged functions in this study, only spatial correlations were studied.

In spatial correlations, for a grid with the distance equal to 0, its spatial correlation coefficient is equal to 1; for an infinite distance, its spatial correlation coefficient is equal to 0.

Therefore, the spatial correlation coefficient of the box filtering is equal to 1 for this grid and is equal to 0 for other grids. Thus, the spatial correlation of the box filtering in the LMS method can be clearly calculated.

3.3 Correlation Functions With RANS and SGS Models

The above discussion shows that it is important to calculate the spatial correlations in coupling to solve LES+SGS equations; therefore, 2 questions arise:

① How can we represent the effects of the correlation functions in the RANS and SGS models?

② Furthermore, are the RANS/SGS models independent of the averaging (RANS) or filtering (LES) operations used in turbulence numerical simulations?

4 Errors in the Theoretical Basis of Turbulence Modeling and Multiscale Turbulence Models

4.1 Basic Consensus and Abbreviation Conventions

To establish the bases for the following discussion, 2 basic statements were first given:

Consensus1 Under a coarse grid, it is impossible to obtain turbulence through numerical simulation of the Navier-Stokes equation.

Consensus2 Only with the DNS grid can complete turbulence be obtained through numerical simulation of the Navier-Stokes equation.

Second, the following abbreviation conventions were used in the discussion.

For the turbulence study, let the Navier-Stokes equation beA=0.

4.2 The Theoretical Basis of the Classical Turbulence Modeling and the Logic Problem

With the LES as an example in the discussion, the results are the same as those of the RANS.

If the LES and SGS equations are coupled solving in the LES grid, i.e.,

(7)

Then, since from consensus 1, one know that turbulence cannot be calculated by the Navier-Stokes equation in the LES grid; therefore, the coupled solution of the LES+SGS equations in the LES grid or the single-scale SGS model approximating the SGS equation has a logic problem.

That is, in the coupled solution of LES+SGS equations, the closer the result is to SGS=0, the less turbulent the solution will be, i.e., there is a contradiction between the purpose and the result, which means there is a logical error; or in the modeling, SGS and not be 0, then, the so-called turbulent results come from unphysical errors of modeling and/or numerical algorithms, which is absurd.

4.3 The Correct Theoretical Basis of Turbulence Modeling and Multiscale Turbulence Models

The basis of correct turbulence modeling theory is equation+grids.

To obtain complete turbulence, the DNS grid shall be used with the Navier-Stokes equation,

(8)

i.e., a multiscale turbulence model shall be used in LES to obtain correct turbulent results.

Notably, since the SGS equation is different from the Navier-Stokes equation used in DNS, the solution of the SGS equation, i.e., the so-called SGS-scale flow field, is conceptually different from the small-scale flow structures obtained by DNS.

However, the computation required to solve the SGS equation on the SGS-scale grid is enormous, even exceeding that of DNS. Therefore, we shall develop a new method (see section 6).

Finally, this type of “modeling” method also appears in other disciplines, so such logic errors widely exist.

5 The Essence and Key of the Closure Problem of Turbulence and the Numerical Method of Solution

5.1 The Essence and Key of the Closure Problem of Turbulence

The closure problem of turbulence is a long-standing unsolved problem in the theoretical bases of turbulence modeling. It is very important to understand the essence and key of the closure problem of turbulence. The closure problem of turbulence can be stated as follows: in the construction of the equation of the SGS-scale correlation terms, there will be more higher-order SGS-scale correlation terms produced in each order of the equation of SGS-scale correlation terms.

First, the closure problem of turbulence is produced in the study of numerical simulation and modeling of turbulence; therefore, the essence of it is not a theoretical problem but a numerical problem.

Second, the key to the closure problem of turbulence is the requirement of the simultaneity of the SGS-scale and the SGS-scale correlation terms, which is similar to the following basic philosophy problem: did the chicken or the egg come at the same time?

Since the Reynolds stress equation of the RANS or LES comes from the fluctuation equation or the SGS equation, it is not necessary to study the Reynolds stress equation but only to use a numerical method to couple the RANS+fluctuation equations or LES+SGS equations to overcome the closure problem of turbulence numerically.

5.2 The Numerical Method for Overcoming the Closure Problem of Turbulence

The method of alternating coupling solutions of the LES and SGS equations is adopted, and the SGS-scale terms obtained at the last moment are used to calculate the SGS-scale correlation terms so that the SGS-scale and SGS-scale correlation terms are not simultaneous. Therefore, the closure problem of turbulence can be overcome with a numerical method.

In fact, in 2000 and 2009, we successfully applied the alternating coupling solution method of the LES equation and the POD low-dimensional dynamical system equation in the numerical simulation of incompressible turbulence[7-8].

6 The LMS Method for Numerical Simulation of Compressible Turbulence

After overcoming the problems in section 2 to section 5, one can now develop the LMS method for the numerical simulation of compressible turbulence.

In the LMS method, the most important innovation is the application of a spatiotemporal multiscale optimal low-dimensional dynamical system of the middle-scale equation to ensure the accuracy of the middle-scale turbulence modeling.

6.1 Predictability of Low-Dimensional Dynamical Systems and Spatiotemporal Intrinsic Bases

In a previous paper[9]on the spatiotemporal optimal low-dimensional dynamical system, there are important findings, such as those shown in fig. 3. In general, low-dimensional dynamical systems with a spatial bases, such as cases of the firtst eight legends in fig. 3 are not predictive, i.e., the solution errors increase with time, and the spatiotemporal optimal low-dimensional dynamical system with a spatiotemporal intrinsic bases, such as the case of last legend in fig. 3, is predictable, i.e., the solution errors can be neglected.

Fig. 3 Predictability of low-dimensional dynamical systems(N=30, Re=2 000)

The key point is the spatiotemporal intrinsic baseξk(x,t), which characterizes the spatiotemporal characteristics of the system. The approximated optimal solution space can be spun with the spatiotemporal intrinsic bases that advance with time and form the spatiotemporal optimal low-dimensional dynamical system with the lowestN, which will be used as the spatiotemporal optimal low-dimensional dynamical system of the middle-scale equation.

(9)

6.2 The LMS Method for the Numerical Simulation of Compressible Turbulence

6.2.1 The Dimensional Compressible Turbulence Large-Scale Equation

The state equation is

p=ρRgT,

(10)

whereRgis the universal gas constant (Rg=287.0).The dimensional compressible Navier-Stokes equations are

(11)

whereEis the total energy,

(12)

where the specific heat ratio isγ=1.4 andMais the Mach number.

Since there are drawbacks with the Favre filter, it was not used in the LMS method. The box filter was applied dimensional compressible Navier-Stokes equations (11), to obtain the dimensional compressible turbulence large-scale equations:

(13)

whererj,τijandqjare middle-scale correlation terms of the LMS method,

(14)

(15)

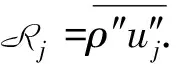
(16)

Qjis the small-scale SGS heat flux term:

Qj=νtCpPrT.

(17)

6.2.2 Equations for the Middle-Scale Dynamical System of Compressible Turbulence

Navier-Stokes equation - large-scale equation=middle-scale equation:

(18)

Function spaces Bu′N, Bρ′Nand BT′Nwere defined, where the research problem is located, to satisfy the conditions as follows:

(19)

u′i=akξki+u′Ri≈akξki,ρ′=bkζk+ρ′R≈bkζk,T′=ckηk+T′R≈ckηk,

(20)

where truncation dimensionNwas omitted.

With spatiotemporal optimal basesξri,ζr,ηr, the spectral expansion equations of dimensional compressible turbulence middle-scale equations (18) were Galerkin formally projected onto unknown bases ofξri,ζr,ηrrespectively, to obtain the equations of the middle-scale dynamic system of compressible turbulence:

(21)

where the coefficients are as follows:

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

6.2.3 The Optimal Functional of Middle-Scale Dynamical SystemJ

The optimal functional for approximating the initial conditions of a dimensional compressible turbulence middle-scale dynamical systemJcan be found below.

With middle-scale optimal bases for approximating the initial conditions of large-scale fieldsξki,ζk,ηk, the following optimal functional can be obtained:

(30)

6.2.4 The Solution Procedure of the LMS Method

At the initial moment, the concept of the turbulence intensity[10-11]was adopted:

(31)

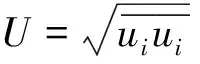
bk(0)=(ρ(0),ζk),ak(0)=(ui(0),ξki),ck(0)=(T(0),ηk).

(32)

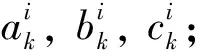
(a) Equations (20) were used to obtain the new solutions of the middle-scale flow field and the correlation functions (14), and small-scale SGS terms equation (15),(16) and (17).

With the middle-scale flow field variables and the correlation functions on the overlapped large- and middle-scale grids and the small-scale SGS terms equation (15),(16) and (17), the terms on the right-hand side of equation (13) were obtained, the new solutions of the large-scale flow field can be obtained by substituting these into large-scale equations (13), and the new solutions of the large-scale flow field were applied to middle-scale dynamical system equations (21).

Equations (30) were used together with the new values of the large-scale flow field interpolated into the middle-scale grid to obtain the new spatiotemporal optimal basesξki,ζk,ηk.

Goto (a) or the LMS simulation is completed.

In this way, the approximate solutions of the turbulence flow field (=large-scale mean field+middle-scale flow field) can also be obtained.

6.3 Numerical Simulation of the Re-Shock Richtmyer-Meshkov Instability Proble m W ith the LMS Method

6.3.1 Problem Description

The initial state of the re-shock RM instability problem is shown in fig. 4.

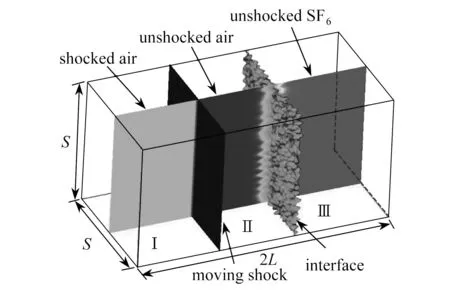
Fig. 4 Schematic diagram of the re-shock RMI initial state in a rectangular cavity

The re-shock RM instability of light/heavy fluid interfaces with multimodal initial disturbances under plane shock acceleration in the shock tube was studied.

D={x|0≤y,z≤S, 0≤x≤2L},

(33)

whereS=0.01 andL=0.014.The numbers of equal spacing grids are flow direction grids×spanwise grids×normal grids=147×61×61=546 987. The time step is 0.000 000 1 s. The shock wave initially located atx=0.01 moves in thexdirection, and the shock Mach number isMaS=1.5.The initial interface is located atx=L, and the initial interface function is

φ(x)=x-L-η(y,z)=0.

(34)

The multimodal perturbation form provided by Tritschler et al. was adopted[12]

(35)

where the main amplitude isa0=4×10-5m, the secondary amplitudes of different modes arean,m=sin(nm)/2, the wavenumbers arekn=2πn/Landkm=2πm/L, and the phase shifts areφn=tan(n) andχn=tan(m).Although equation (35) is similar to the form of random perturbation, it has a definite expression and can be repeatedly constructed in different examples.

The light/heavy fluids on both sides of the interface are composed of air/SF6components, and their molar masses areM1=28.964 g·mol-1andM2=146.057 g·mol-1, respectively. The initial pressure and temperature were set top0=23 000 Pa andT0=298 K, respectively. Then, the density was obtained from the equation of state (10):

(36)

i.e.,

(37)

(38)

The atwood number is

(39)

6.3.2 Initial and Boundary Conditions

1) The initial condition

In summary, it can be seen that in the study of RM instability, the fluid inside the shock tube at the initial moment is divided into 3 regions by the shock wave and interface: light fluid behind the wave (zone Ⅰ), light fluid before the wave (zone Ⅱ), and heavy fluid before the wave (zone Ⅲ). The light fluid after the shock wave needs to be determined on the shock wave, before and after, under the Rankine Hugoniot condition[13], and the specific heat ratio isγ1=1.4.The specific expression of the density is as follows:

(40)

The pressure can be expressed as:

(41)

Finally, the velocity can be represented as:

(42)

The temperature was also determined by equation of state (10) as

(43)

Therefore, the initial conditions for the RM instability problems can be summarized as follows:

(44)

(45)

(46)

(47)

where H is the Heaviside function

(48)

The error function were used to perform the following smoothing operations:

(49)

2) The boundary condition

The RM instability satisfies the periodic boundary conditions in theyandzdirections, and the boundaries in thexdirection are non-slip solid walls.

6.3.3 Numerical Results of the Re-Shock Richtmyer-Meshkov Instability

The parameters used in the following numerical results of the re-shock Richtmyer-Meshkov instability are the dimensions of the spatiotemporal multiscale optimal low-dimensional dynamical system of middle-scale equationN=3, Reynolds numberRe=3 608 549, Mach numberMa=0.6, Prandtl numberPr=0.72 and simulation timet=0～0.002 4 s. In following figures, the upper, middle and lower figures show the iso-surface of the middle-scale fields, the large-scale mean fields, and the approximate solutions of turbulence, respectively.

(a) t=0.000 1 (b) t=0.000 2 (c) t=0.000 3 (d) t=0.000 4 (e) t=0.000 5

From figs. (5) to (9), it can be seen that the RM instability interface is repeatedly rubbed by the re-shock wave to produce a large number of smaller flow structures close to the middle part in the middle-scale and large-scale flow fields, and to obtain another kind of very interesting approximate solution of turbulence other than that of DNS for the first time.

(a) t=0.000 1 (b) t=0.000 2 (c) t=0.000 3 (d) t=0.000 4 (e) t=0.000 5

Because the purpose of this paper is to point out that there are a few big problems in the theoretical bases of turbulence modeling, and then setup a new and multi-scale numerical simulation method for compressible turbulence (LMS), therefore there is no need to conduct a careful physical analysis of the results.

Since the LMS method is a new independent numerical simulation method for turbulence based on the first principles and without any artificial assumptions, its theoretical basis is consistent; therefore, it is not necessary to verify its correctness through quantitative comparison with DNS coarse-grained results.

It must be noted that it is wrong to directly compare the numerical results of the RANS, LES, DES or LMS with those of the DNS. The correct method is to first coarse-grain the DNS numerical results on the RANS, LES, DES or LMS grids and then compare their results quantitatively.

(a) t=0.000 1 (b) t=0.000 2 (c) t=0.000 3 (d) t=0.000 4 (e) t=0.000 5

7 Conclusions

According to Professor ZHOU Peiyuan’s idea[2]in which “the turbulence should be studied by analyzing and solving the fluctuating velocity field”, we reviewed the theoretical bases of turbulence modeling before setting up the LMS method and examined the following aspects.

Based on the physical characteristics of turbulence, a new concept of large-, middle- and small-scale decompositions of turbulence was proposed. The relationship between the correlation function and the filtering (averaging) function was analyzed, and the algorithm for the correlation function clarified. A long-standing logical error in the theory of turbulence models was pointed out, and the correct theoretical bases of the numerical simulation of turbulence and the concept of a multiscale turbulence model were given. The philosophical essence was indicated, and an iterative multiscale method was successfully employed to overcome the closure problem of turbulence. The errors in the quantitative comparison of turbulence numerical simulation results were studied, and a coarse-grained quantitative comparison method was provided.

Then, the LMS method was systematically established, and the turbulent middle-scale flow field and the spatiotemporally accurate solution of turbulence were obtained with the LES grid, which deepens the understanding of the complexity of turbulence. The multiscale characteristics of turbulence are naturally included in the middle- and small-scale modeling, there is no logic error in the LMS method, and the approximate solution of turbulencefcan be obtained. Due to the use of the first principles in the LMS method, the LMS method is suitable for the numerical simulation of various complex turbulent flows, and fewer grid points can be used in the LMS method to obtain a more accurate solution of turbulence. With the box filtering and the space grid average, and in the sense of a large-scale grid, the essence of the LMS method is a turbulence numerical simulation method integrating the RANS, LES, DES and DNS.

Finally, it is necessary to indicate that the LMS method can also serve as an auxiliary tool for turbulence model research to examine whether the turbulence model corresponding to each term in the SGS-scale (fluctuations) equation is correct.