基于三维随机集料的钢渣沥青混合料微波加热和冷却过程温度模拟

陈雪琴, 万保才, 王宇豪, 董 侨, 姚 辉

(1.南京理工大学土木工程系, 南京 210094; 2.安徽淮南平圩发电有限责任公司, 淮南 232089;3.东南大学交通学院, 南京 211189; 4.北京工业大学城市建设学部, 北京 100124)

沥青是一种典型的自修复材料[1]。在休息期内,沥青中部分微裂纹能够自修复。微裂纹愈合效率与荷载循环次数、孔隙率、沥青含量、温度等因素有关。其中,温度是影响沥青微裂纹自愈能力的主要因素[2]。研究人员发现,从分子动力学的角度来说,沥青自愈合机理是沥青分子从一个裂纹面向另一个裂纹面的扩散、润湿。因此,温度的升高可以加速裂纹表面沥青分子的润湿和扩散速率,显著缩短自愈合时间并提高自愈合速率[3]。

微波加热具有加热速度快、加热深度深、温度分布均匀等特点[4]。因此,微波加热具有应用于沥青混凝土路面养护和除冰领域的良好潜力[5]。Norambuena-Contreral等[6]制备了4种掺不同含量的钢丝绒纤维沥青混合料半圆弯曲试件,以愈合前后强度比为愈合指标,分别研究微波加热和感应加热对沥青混合料自愈合的影响,结果表明微波加热可以更有效地治愈沥青路面的裂缝。张振华等[7]将钢渣粉等工业废弃物加入普通混凝土中以增强其微波吸收性能,试验结果表明在微波作用下混凝土表面的升温速率随钢渣粉掺量的增加而增加,因而冰层脱落时间明显缩短,微波加热有利于路面除冰。钢渣作为一种炼钢副产品,具有防滑性和耐磨性好、强度高、耐久性好等特性[8],利用钢渣集料替代天然集料可以改善沥青混合料的性能,降低天然碎石集料成本,减少钢渣堆积对土地资源占用,提高钢渣利用率。钢渣主要由CaO、MgO、Al2O3、SiO2和 Fe2O3等组成[9],具有良好的介电损耗和磁损耗,且以介电损耗为主[10]。因此将钢渣加入沥青混合料中,能提高沥青混合料整体的微波吸收能力。

为研究微波加热过程中温度分布,可以采用室内加热试验。已有研究表明,微波加热时间过长可能导致局部过热现象[11]。由于钢渣集料占混合料的大部分体积,钢渣沥青混合料在微波加热下呈现出优良的升温特性,经过120 s的微波加热,其整体平均温度由19.7 ℃提高到了70.9 ℃,整个马歇尔试件中钢渣均能受到均匀的微波加热,因此表现出了更加均匀的温度场分布现象[12],钢渣沥青混合料局部过热不明显[11]。沥青混合料温度不宜超过100 ℃,否则会造成试件变形严重、膨胀松散和沥青老化[13-15]。Liu等[16]将沥青混合料加热至100 ℃,从加热后与未加热的试件中取出沥青,采用傅里叶变换红外光谱仪(Fourier transform infrared spectrometer,FTIR)分析表明加热后的沥青未老化。此外,Garcia等[17]采用凝胶渗透色谱(gel permeation chromatography,GPC)测量未加热和加热后的沥青(加热至110 ℃)分子量,结果表明加热前后沥青分子量未发生变化,不会造成沥青老化。二者结果最主要的原因是短时间的加热不会引起沥青额外的老化。

微波加热时沥青混凝土试件的温度分布不均匀,研究中通常用红外热成像仪获得试件表面温度分布,用温度传感器获得试件内部温度分布。Wei等[18]发现微波加热时,钢渣有利于提高乳化沥青修补材料温度分布的均匀性,乳化沥青修补材料的内部平均温度高于表面平均温度。向阳开等[19]分别研究了微波加热下沥青混合料上表面和下表面的加热速率差,结果表明随着深度的变化,上下加热速率差异变小。说明温度分布差异性不仅存在于试件的内部和外部,在试件的表面也同样存在。

微波加热是一个多物理场耦合现象,其中涉及电磁加热和固体传热。首先,施加在导电材料上的任何电场都会产生涡流,而施加在导电材料上的时变磁场也会诱导电流流动。此外,时变电场会使材料内的偶极分子来回振荡,产生分子摩擦,从而产生热量。为了模拟沥青混合料的微波加热过程,可以利用相关有限元软件,如CST、COMSOL[20]等。Benedetto等[21]在CST软件中建立微波加热模型,根据室内试验确定混合料的参数、微波参数仿真参数,结果表明室内试验和仿真结果吻合度较高。王升[22]使用COMSOL软件建立了微波加热时路面冰层的仿真模型,分析了除冰模型在不同加热时长下的温度场分布以及结合层特征点处的温度变化。Wei等[23]使用COMSOL Multiphysics建立多场模型来模拟单骨料混凝土试件的微波加热过程,研究微波加热功率、频率和持续时间对砂浆-骨料界面温度和应力梯度的影响。

由于均质模型无法很好地揭示沥青砂浆和集料之间的温度差异性,因此需要建立非均质沥青混合料三维细观微波加热模型。已有研究多数仅局限于微波加热过程,但冷却过程通常远比加热过程长,且自愈合现象在冷却过程仍然会持续发生,因此需要进一步研究冷却过程沥青混合料温度变化规律。本文利用COMSOL与MATLAB联合仿真,基于蒙特卡洛原理随机生成三维集料,建立了透水沥青混合料试件的三维细观模型,采用钢渣集料部分替换玄武岩粗集料(4.75～9.50 mm、9.50～13.20 mm),构建普通玄武岩集料试件(PAC-B)、普通钢渣粗集料试件(PAC-US)以及改性钢渣粗集料试件(PAC-MS)3种沥青混合料试件,对其连续加热、冷却过程进行模拟,研究沥青混合料不同材料之间的传热机理。

1 试验材料

1.1 沥青

透水沥青混合料的孔隙率较大、粗集料含量较多[24],为了防止在微波加热过程中出现沥青混合料试件出现松散和剥落,采用高黏度改性沥青以增强对于集料颗粒的裹覆。高黏度沥青性能指标和技术要求如表1所示。

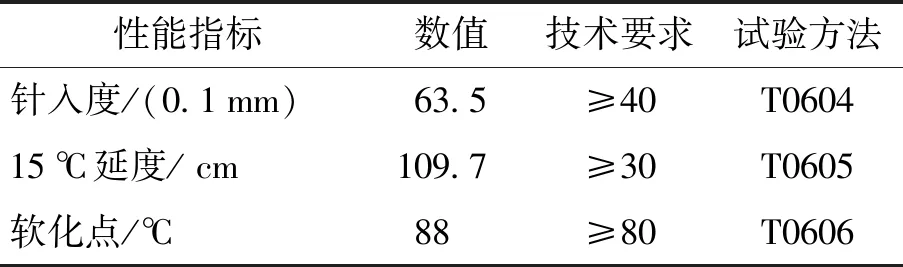
表1 高黏度改性沥青技术指标

1.2 集料

透水钢渣沥青混合料的集料包括玄武岩集料和钢渣集料。其中粗集料质量分数较多(约占80%),粗集料由于相互嵌挤形成骨架-空隙结构,其作用就是充当混合料的矿质骨架。玄武岩具有抗压性强、耐磨损、与沥青具有较好的黏附性等特点,常常用作沥青混合料的集料。钢渣作为炼钢后剩余的工业废料,其力学性能也较能满足道路工程的使用,相比于天然形成的矿物集料更易获得。钢渣和玄武岩的试验指标如表2所示。设计级配如表3所示。

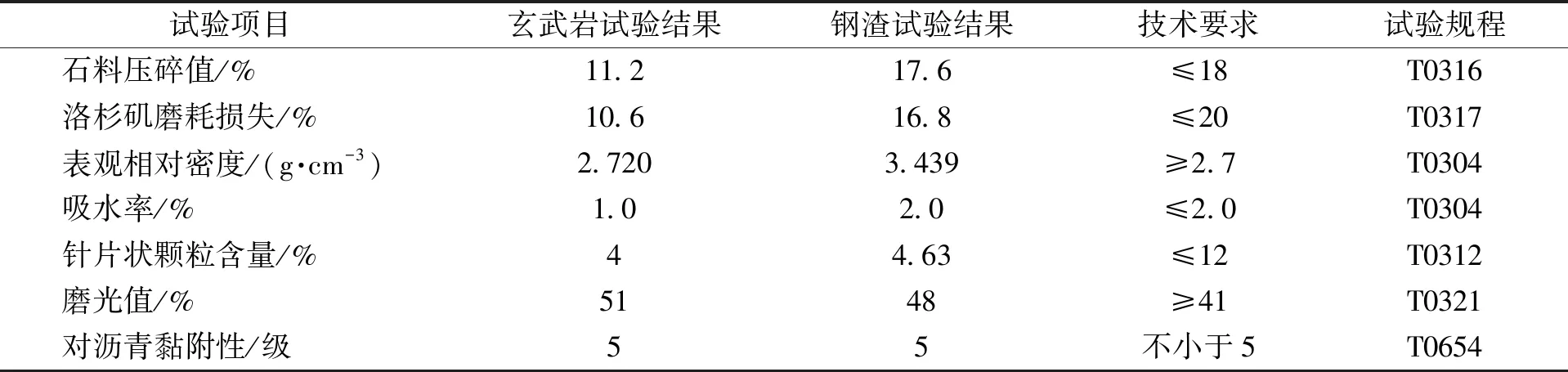
表2 集料试验指标

表3 PAC-13透水沥青混合料设计级配

1.3 钢渣改性试验原理

为了进一步增强透水沥青混合料微波吸收能力,可对钢渣集料进行改性处理。钢渣改性方法主要采用化学共沉淀法[25],共沉淀法具有产品纯度高、反应温度低、颗粒均匀等优点[26]。化学共沉淀法可以在钢渣集料表面生成高磁损耗的Fe3O4颗粒,从而增强其吸波性能,其原理如下:

(1)

使用波导法测量试件的电磁参数,结果表明改性钢渣混合料的电磁损耗大于普通钢渣混合料和普通玄武岩混合料,说明改性钢渣混合料的吸波性能大于后两者。

基于文献[27],本文采用普通钢渣、改性钢渣替换玄武岩粗集料,且替换率为50%。分别成型普通玄武岩集料试件(PAC-B)、普通钢渣粗集料试件(PAC-US)以及改性钢渣粗集料试件(PAC-MS)以研究其温度分布规律。

2 模型构建

2.1 三维随机集料生成算法

在COMSOL软件中,可以借助其与MATLAB的接口COMSOL with MATLAB编写脚本文件,从而实现三维随机集料的创建[28]。

蒙特卡洛方法是一类随机方法的统称,其思想核心是通过随机模拟出来的大量样本集去近似研究实际问题对象。根据随机分布理论将骨料随机投放到基体中,可以建立和实际混凝土相近的细观模型[29]。而沥青混合料试件在实际成型的过程中,集料充分搅拌,因此可以假设集料在试件中是随机分布的,根据级配曲线,基于蒙特卡洛方法随机生成三维集料。

本本将粗集料简化为三维球体,沥青混合料试件简化为半圆柱体。由于细集料和矿粉的颗粒数量巨大,为节约计算成本,本文没有采用全级配的随机集料,而是将细集料、填料、沥青组成的沥青砂浆视为整体均质模型,仅随机生成粒径大于2.36 mm的集料颗粒。根据设计级配(见表3)可以得到 2.36～4.75 mm、4.75～9.50 mm、9.50～13.20 mm共3档粒径集料的质量比。根据集料的质量比,计算了半圆柱沥青混合料试件每一档集料颗粒的质量,根据粗集料密度即可近似得到每一档集料的体积。当每一档集料的体积满足要求时,则自动开始生成下一档集料的生成循环,直到粗集料全部生成完毕。各档粗集料的质量分数、体积分数、体积以及生成的集料个数如表4所示。根据表4的结果,在MATLAB中按照COMSOL提供的参数化语言根据

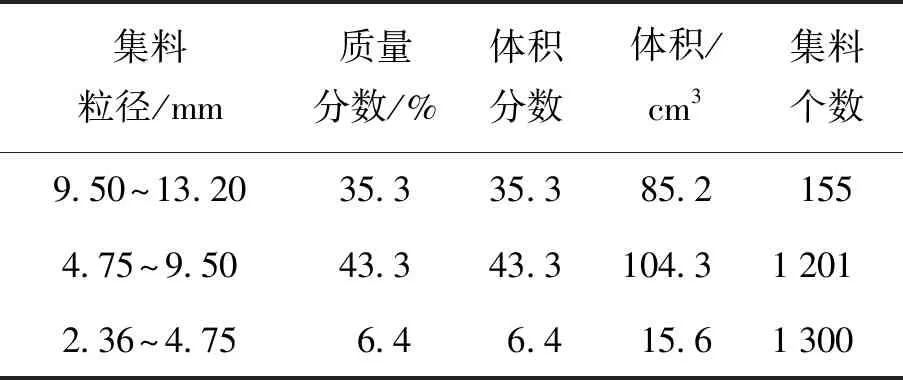
表4 粗集料质量分数与体积

x0=rscosφ, 0≤φ≤π

(2)

y0=rssinφ, 0≤φ≤π

(3)

0≤z0≤hs

(4)

(5)

x0-(1+γ)r0≥0

(6)

y0-(1+γ)r0≥0

(7)

z0-(1+γ)r0≤hs

(8)

(9)

编写生成随机集料的程序。式中:(x0,y0,z0)表示随机生成集料球心位置坐标;r0为半径;rs表示半圆柱体半径;hs表示半圆柱体半径高度。

值得注意的是,在COMSOL中划分网格时,如果三维区较薄会使得划分网格的质量较低,从而影响仿真结果的准确性。为了防止生成的随机几何模型中存在较薄区域,外边界条件和互不相交条件的判别式中还应控制集料之间、集料与边界之间的最小距离,可以使用放大因子γ控制,考虑到沥青膜的厚度以及集料间距,γ取0.02。在生成粗集料的过程中,随着集料投放空间的不断缩小,投放效率不断降低,新生成的集料所用的时间增加,而放大因子可以使粒径较小的集料实现充分填充。最终生成的非均质试件模型如图1所示。

图1 非均质试件模型

2.2 微波加热原理

室内加热的微波炉产生的是一种高频率的电磁波,频率为2.45 GHz,即磁场方向1 s改变24.5亿次,对于时变的电磁场可以使用麦克斯韦电磁方程组的复数形式,表达式为

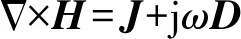
(10)

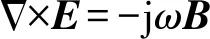
(11)

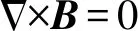
(12)

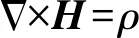
(13)

微波进入沥青混合料内部会将微波能转化为热能,从而产生热量。当沥青混合料内部存在温差时,热量会从高温处传导至低温处。微波加热时,温度T是关于空间位置和时间的函数,即T=T(x,y,z,t)。固体的热传导方程为

(14)

式中:ρ为固体材料的密度;Cp为定压热容;k为导热系数;Qd为热流密度。

2.3 自然冷却原理

对流换热一般有自然对流和强迫对流2种方式。自然对流是在没有外部风力推动时,由于温度场不均匀造成流体密度分布不均匀,流体产生浮动力所引起的换热。显然,沥青混合料与空气相接触的界面上会发生自然对流换热。根据牛顿冷却定律,当物体表面与周围存在温度差时,单位时间从单位面积散失的热量与温度差成正比,比例系数称为对流换热系数,即

Δt=|tw-tf|

(15)

q=hΔt

(16)

(17)

式中:Δt为温度差;q为热流密度;h为物质的对流换热系数;Φ为传热功率;A为传热面积。

2.4 COMSOL模拟微波加热过程

简化的数值模型包含微波炉内腔、波导、沥青混合料试件以及具有较好耐热性能的方形陶瓷底板。微波炉内腔为340 mm×343 mm×193 mm的长方体,微波炉内壁表面(包括微波炉门)简化为具有不锈钢物理参数的零厚度表面。波导简化为50 mm×78 mm×25 mm的长方体。陶瓷底板为270 mm×270 mm×6 mm的长方体,厚度为6 mm。在加热和冷却过程中,试件在微波炉中的散热可视为外部自然对流,即试件的外表面通过自然对流耗散热量,这一损耗的特征可以使用对流传热系数h来表征。COMSOL中的“传热模块”提供传热系数函数,可以在“对流热通量”选项中进行设置。微波加热模型,如图2所示,耦合了“电磁波”和“固体传热”2个物理场,可以模拟微波加热过程中的电磁场和温度场。冷却过程不存在电磁场,只有表面散热和内部传热。

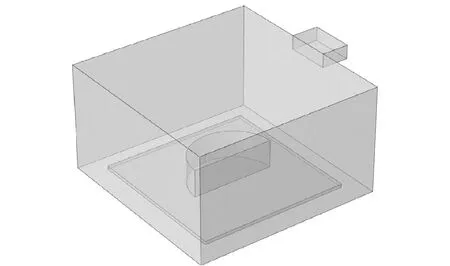
图2 微波加热模型示意

2.5 材料参数设置

透水沥青混合料试件孔隙率约20%,为了模拟试件孔隙率,可以将试件设定为多孔介质,其中设定孔隙的比例与试件的空隙率近似相等。多孔介质的固体传热方程为

(18)

式中:ρs和Cp,s分别为沥青砂浆(不包含空隙)的密度与定压热容,ρs取1 450 kg/m3,Cp,s取1 680 W/(m·K);ρf和Cp,f分别为空气(空隙中空气)的密度与定压热容,2个参数均是温度的函数;keff是有效导热系数,其值取决于多孔介质中固体和流体的导热系数,本文按默认值取体积平均计算导热系数,即

keff=(1-θ)ρsCp,s+θρfCp,f

(19)

式中:θ为多孔介质孔隙占试件的体积比,本式中取0.2。

对于钢渣集料试件,由于只有4.75～9.50 mm、9.50～13.20 mm这2种粒径使用普通钢渣或改性钢渣替换,而其他部分的材料没有变化,因此PAC-US、PAC-MS这2种试件仅仅在这2种粒径范围内的集料属性上有所区别。试件模型的材料属性如表5所示。

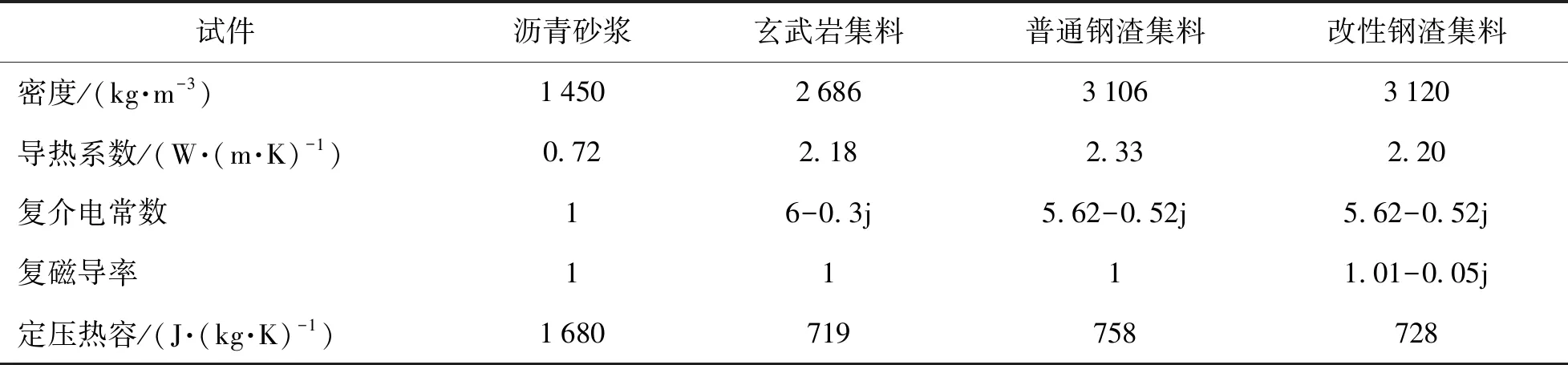
表5 沥青混合料不同材料属性

2.6 网格划分

非均质模型可以根据物理场划分自适应网格。将模型设置为联合体,在不同材料区域的边界处生成过渡性的面网格,即边界两边的网格共享相同的节点和面,而非各自独立。因此,尽管试件内部不同区域材料的参数不同,但是在内部边界仍然可以保持通量与场的连续性。COMSOL中自动生成的试件模型网格与集料网格如图3所示。

3 非均质模型连续加热及冷却过程仿真

3.1 加热过程温度

在COMSOL中,表面温度云图显示的是试件或材料表面的温度分布,体积温度云图则显示的是试件或材料整个三维实体的温度分布。因此,根据后处理结果可得普通玄武岩集料试件(PAC-B)普通钢渣粗集料试件(PAC-US)与改性钢渣粗集料试件(PAC-MS)在微波加热120 s后的内部集料的表面温度,如图4～6所示。

图4 PAC-B连续加热120 s温度分布

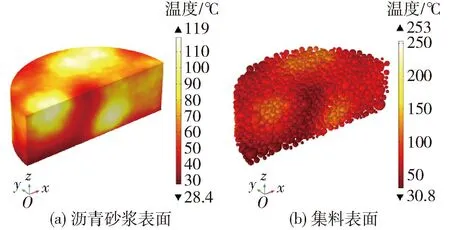
图5 PAC-US连续加热120 s温度分布

图6 PAC-MS连续加热120 s温度分布

可以看出,连续加热120 s后,PAC-B、PAC-US、PAC-MS的集料表面最高温度分别是 235、253、235 ℃,而沥青砂浆表面最高温度则分别是124、119、136 ℃。集料表面的温度分布区域和沥青砂浆表面的温度分布区域一致,且集料的表面最高温度远大于沥青砂浆的表面最高温度,集料的表面最低温度也大于沥青砂浆的表面最低温度,说明微波加热过程中集料向沥青砂浆传热,从而引起沥青砂浆的升温。仿真结果在细观尺度上说明了集料与沥青砂浆二者吸波能力的差异性。根据生成三维随机集料的原理可知,粗集料为3种粒径的球体颗粒的集合,沥青砂浆则是在半圆柱体内集料之外区域的集合。集料为沥青砂浆所包裹,且沥青砂浆中包含孔隙,孔隙的存在会使得导热系数降低,从而降低温度的传导效率。此外,同一种试件的粗集料也显示出不均匀的温度分布,说明集料粒径也可能影响集料的温度分布。

从沥青砂浆的表面温度分布可以看出,上表面和前表面存在多个高温区域。从宏观角度看,PAC-US与PAC-MS的沥青砂浆表面温度分布基本一致,但PAC-MS的最高温度高于PAC-US。由于2种试件的沥青砂浆的材料属性基本相同,说明经过改性的钢渣粗集料的传热效果优于普通钢渣粗集料。此外,3种试件的靠近底部的温度较低,说明试件与底盘之间也存在少量的热量耗散。

3.2 集料升温速率

分别提取2.36～4.75 mm、4.75～9.50 mm、9.50～13.20 mm集料的体积温度,进行线性拟合可以得到不同试件的集料体积温度随时间的变化图。如图7所示,可见每种粒径集料的体积平均温度也随着时间呈线性变化。在加热120 s后,PAC-B由粗到细3种粒径集料的体积平均温度分别为84.3、89.8、81.3 ℃,升温速率分别为0.493、0.532、0.470 ℃/s;PAC-US由粗到细3种粒径集料的体积平均温度分别为96.5、101.8、92.2 ℃,升温速率分别为0.594、0.631、0.564 ℃/s;PAC-MS由粗到细3种粒径集料的体积平均温度分别为106.5、112.8、101.7 ℃,升温速率分别为0.678、0.721、0.644 ℃/s。对于同一种试件,随着粒径的增加,体积平均温度先升高后降低,且与该粒径集料的材料性质无关。4.75～9.50 mm集料的升温速率高于2.36～4.75 mm集料、9.50～13.20 mm集料。由升温速率可知,相同粒径的体积平均温度由高到低依次为改性钢渣集料、普通钢渣集料、玄武岩集料,说明改性钢渣集料与普通钢渣集料的吸波能力均强于玄武岩集料,2种钢渣集料都可以提升微波加热的效率。

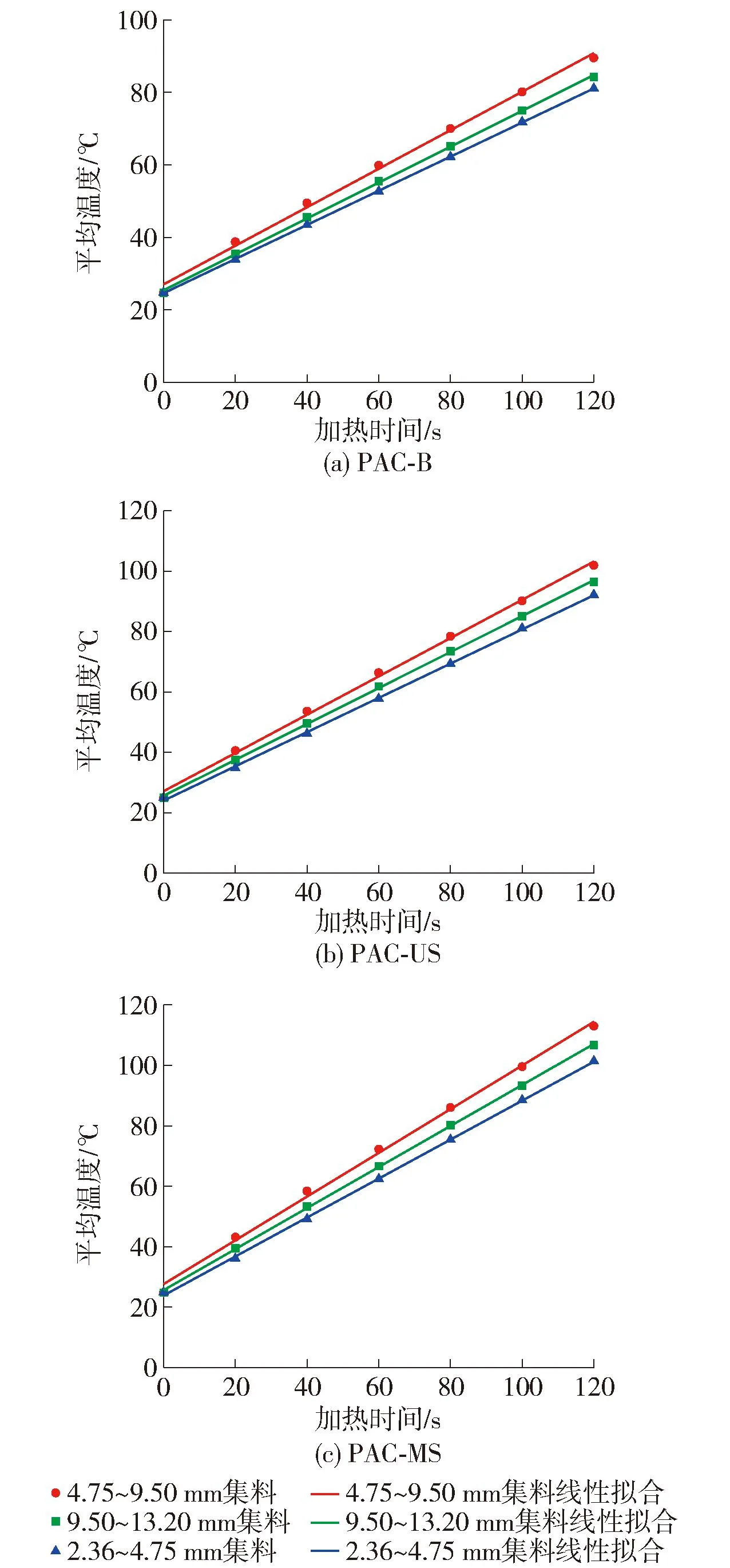
图7 不同试件的集料体积温度变化

3.3 冷却过程温度

图8～10分别给出PAC-B、PAC-US、PAC-MS冷却10、20、30、40 min后集料表面与沥青砂浆表面的温度分布。

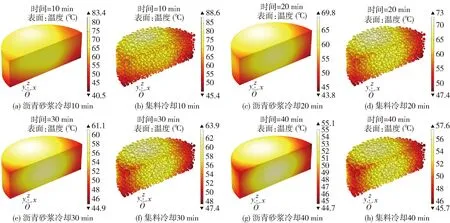
图8 PAC-B冷却过程温度变化

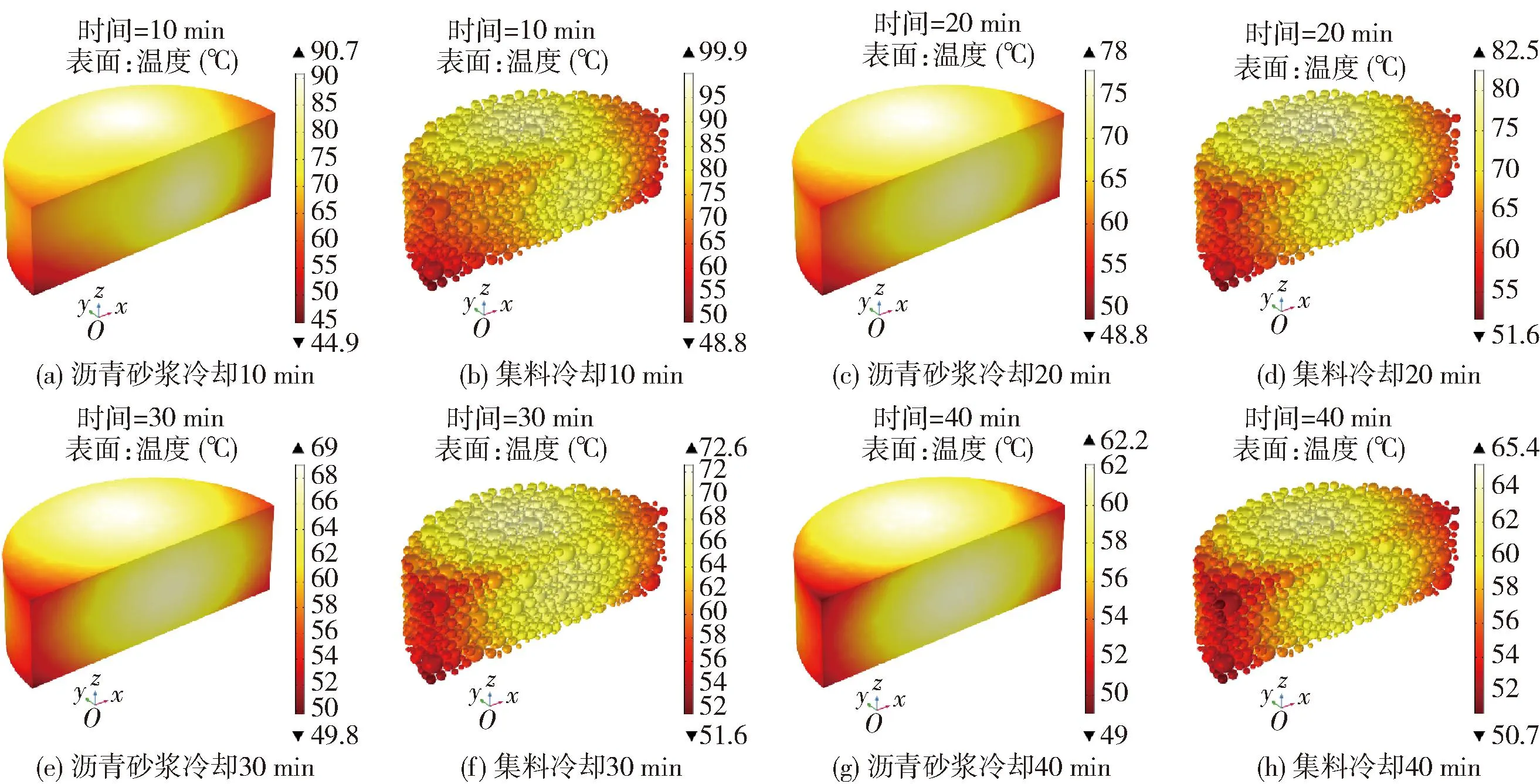
图9 PAC-US冷却过程温度变化

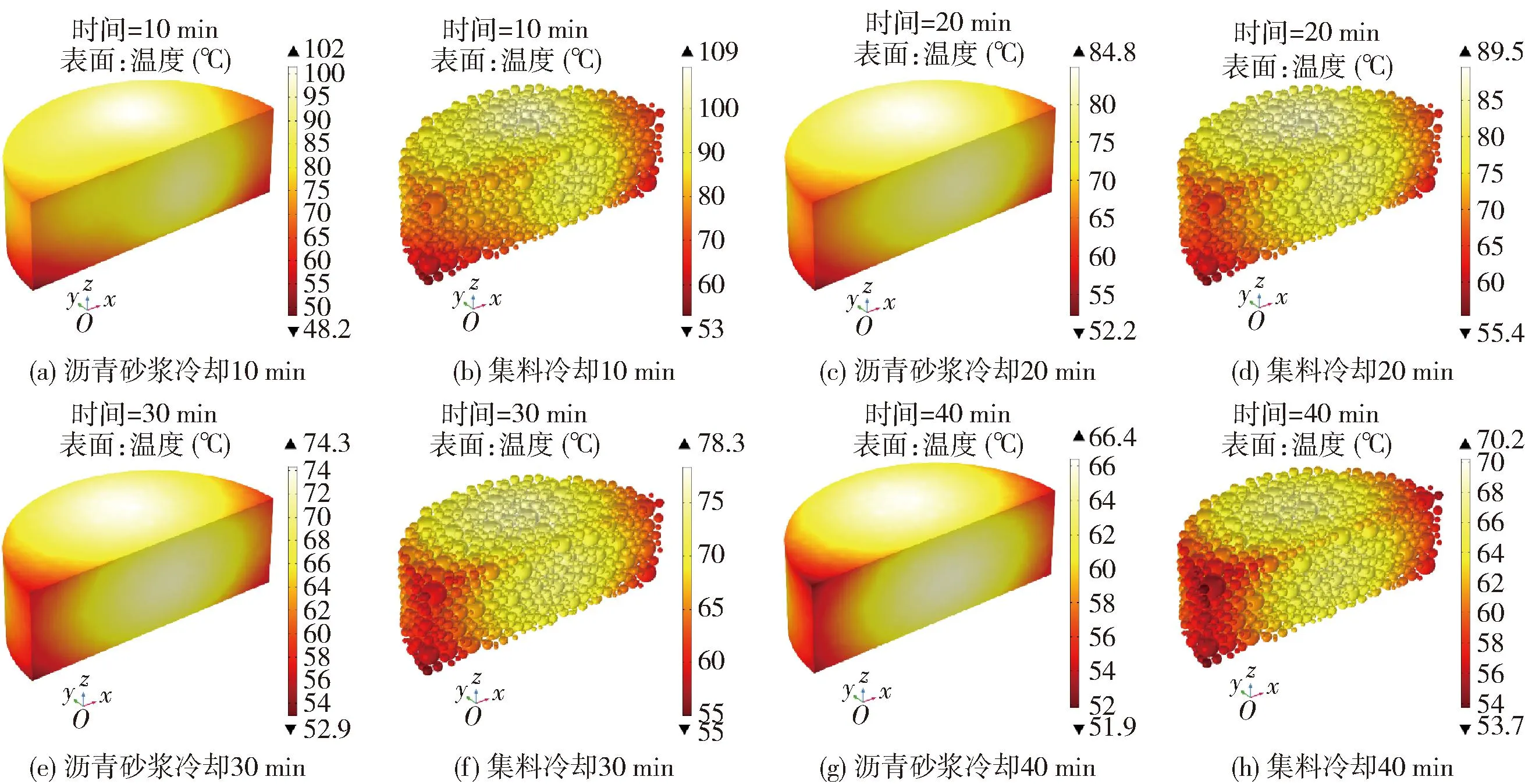
图10 PAC-MS冷却过程温度变化

与加热过程类似,冷却过程中集料和沥青砂浆的温度分布区域也基本一致,说明在冷却过程中,沥青砂浆和集料之间也存在热量传导,且集料的表面温度始终高于沥青砂浆的表面温度。

在集料冷却的过程中,最低温度先上升后下降,最高温度则不断下降,说明粗集料内部也存在热传导现象。在微波加热过程中,吸波能力较好的集料温度较高,吸波能力较差的集料温度则较低。在冷却过程中,由于微波加热的停止、电磁场消失,在试件内部仅存在传热场。由于温度差的存在,热量由温度较高的集料向温度较低的集料传导,集料之间的温差减小。然而随着冷却时长的不断增加,热能将不断耗散,集料的最低温度将在上升之后下降。沥青砂浆冷却过程的规律与集料相似,即最高温度不断下降,最低温度先上升后下降。

冷却过程中3种试件的粗集料最高温度由大到小依次为PAC-MS、PAC-US、PAC-B。由此可见,在加热过程中,虽然PAC-US的集料最高温度高于PAC-MS的集料最高温度,但在后续冷却时却低于PAC-MS,说明改性钢渣集料与普通钢渣集料在传热性能上也存在差异。

4 非均质模型结果与试验结果对比

为验证非均质模型模拟微波加热和冷却的合理性,将室内试验结果和非均质仿真结果进行对比。PAC-US试件如图11(a)所示,在微波炉连续加热120 s的温度分布如图11(b)所示。图11(b)中,Sp1点、Sp3点、Sp4点测的是集料温度,温度值分别为107.1、113.8、91.9 ℃。Sp2点、Sp5点、Sp6点测的是沥青砂浆温度,温度值分别为81.7、88.5、86.1 ℃,可见集料表面温度高于沥青砂浆表面温度。

图11 PAC-US试件连续加热120 s温度分布

加热结束后立即打开微波炉门,将试件置于自然状态下冷却。为了使试件不发生剥离和散落,需要充分冷却。设置总冷却时间为40 min,图12(a)为PAC-US试件冷却20 min的温度成像结果,图12(b)为 PAC-US试件冷却40 min的温度成像结果。图12中Sp1点测的是沥青砂浆的温度,Sp2点、Sp3点测的是集料温度。冷却20 min时,Sp1点、Sp2点、Sp3点的温度分别为69.3、56.6、66.2 ℃;冷却 40 min时,Sp1点、Sp2点、Sp3点的温度分别为53.4、47.2、50.4 ℃。

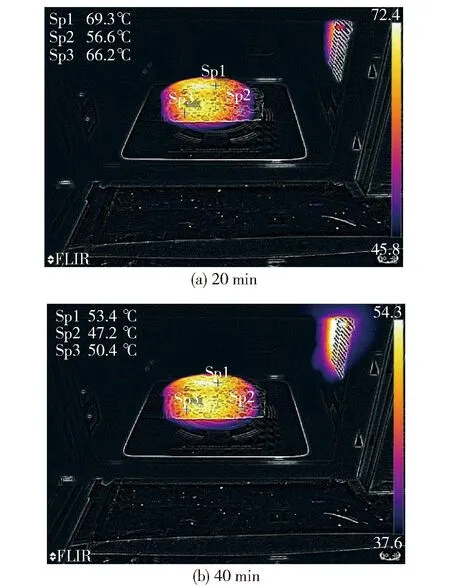
图12 PAC-US自然冷却过程温度分布

采用非均质模型模拟PAC-US连续加热,得到加热120 s后沥青砂浆表面和集料表面温度分布(见图5),可以看出集料表面温度高于沥青砂浆表面温度。PAC-US试件连续加热后在不同试件高度处的温度变化曲线如图13所示,可以看出,室内试验和数值仿真结果的温度分布区域基本一致。

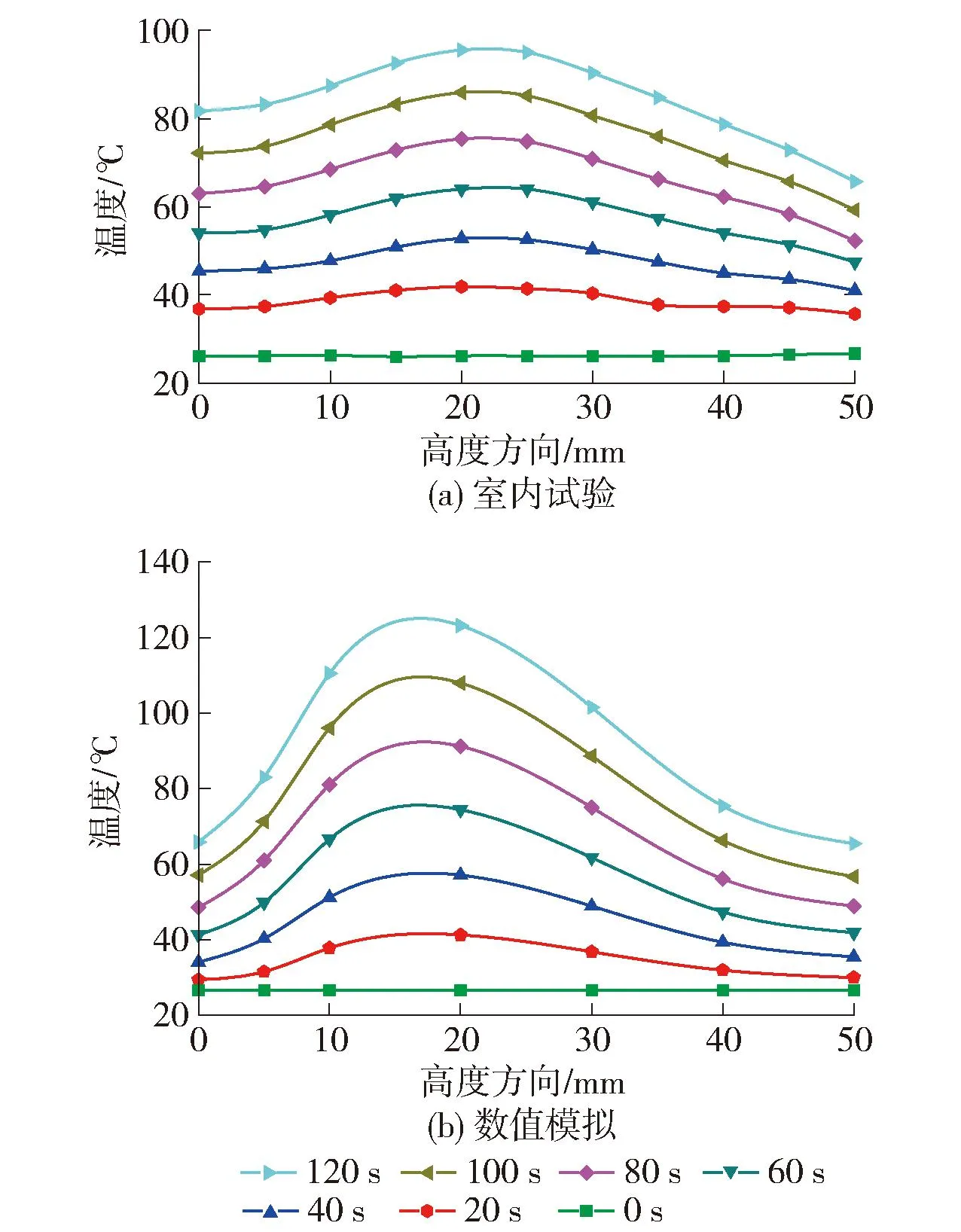
图13 PAC-US连续加热后不同试件高度处的温度曲线

采用非均质模型模拟PAC-US冷却过程,得到冷却20、40 min后沥青砂浆表面和集料表面温度分布,分别如图9(c)(d)、图9(g)(h)所示。可以看出数值模拟的结果与室内试验结果相同,二者温度分布区域基本一致,说明采用本文的非均质模型模拟微波加热和自然冷却过程均是可行的。PAC-B、PAC-MS试件加热和冷却过程的室内试验和数值模拟的对比结果与PAC-US试件类似,此处不再赘述。

5 结论与展望

为研究钢渣透水沥青混合试件在微波加热和冷却过程的温度变化规律,本文根据蒙特卡洛方法随机生成符合级配的粗集料,建立了非均质三维仿真模型,分别定义沥青砂浆、玄武岩粗集料、钢渣粗集料的材料参数,模拟微波加热及冷却过程。从细观尺度分析透水沥青混合料的温度场变化,揭示沥青砂浆、粗集料之间的导热规律。通过对比PAC-B、PAC-US、PAC-MS这3种试件的温度场变化,可以得出如下结论:

1) 无论是加热过程还是冷却过程,沥青砂浆的表面温度分布区域与集料表面温度分布区域均一致,且集料表面的最高温度要大于沥青砂浆的表面最高温度,说明集料吸波能力强于沥青砂浆,由于温度差的存在,集料可以向沥青砂浆传导热量。集料在冷却过程中的最高温度不断降低,而最低温度则先升后降。

2) 对于同一种试件,集料高温区域较为集中,且同时包含2.36～4.75 mm、4.75～9.50 mm、9.50～13.20 mm这3种不同粒径的集料,说明同种试件里不同集料的性质不影响其集料的温度分布。集料体积平均温度的升温曲线则表明,集料体积平均温度不会随着粒径的增加而升高,而是先升高后降低。粒径4.75～9.50 mm范围内的集料体积平均温度最高。

3) 加热过程中PAC-US的温度都高于PAC-B。在冷却过程中,2种钢渣集料试件的温度也高于PAC-B。

4) 以PAC-US连续加热和冷却为例,将非均质模型结果与室内试验结果对比,结果吻合度良好,表明用非均质模型模拟微波加热与冷却过程温度变化具有可行性。

对于实际路面的微波加热过程,需结合现场试验确定微波加热影响范围,据此确定加热路面尺寸,基于本文提出的方法建立路面的三维模型。根据微波加热设备确定其尺寸、功率、波导尺寸等,从而实现实际路面的微波加热过程模拟。