一种改进的非协作MSK 信号参数联合估计算法

郭 辉，费曰振，谷加臣，闫博文，李卓宇

（中国人民解放军63889 部队，河南 孟州 454750）

0 引言

最小频移键控（MSK）是一种以改变波载频率来传输信息的调制技术，即特殊的连续相位的频移键控。MSK 调制方式具有较高的功率利用率和频谱利用率［1］，广泛应用于军事通信领域，如被应用于美国国家航天局的高级通信技术卫星系统和美军的Link16数据链等通信系统中［2］。调制参数的复杂性及较高的频谱利用率，给电子对抗侦察分析及情报获取带来困难。

MSK 信号参数估计主要包括载频、符号周期和调制指数参数估计［3］，目前基于信号循环平稳性［4］的载频、符号周期和调制指数的联合估计算法［5-6］等较为成熟。但其算法的抗噪声性能不强，算法较复杂，运算量较大。针对这些局限，本文提出一种改进的联合估计算法，采取功率谱法来估计载频，可以有效地抑制噪声的影响，提高参数估计的精度；同时改变算法搜索方式，降低搜索次数，从而降低运算量。改进的联合估计算法可以在低信噪比条件下快速对载频、符号周期和调制指数进行参数估计。

1 MSK 信号模型

MSK 信号为成形脉冲为矩形的连续相位调制（CPM）信号，CPM 信号的表达式通常为：

式中，符号周期为Ts，信号的能量为E，通常情况下假设（2E/Ts）1/2=1，fs为载波频率，ϕ(t)表达式为：

一般取调制阶数M=2l，l=1，2，…；表达式中，hk为调制指数，ak为调制的信息序列，q(t)为调制信号的相位响应脉冲。

q(t)一般表示为：

式中，g(t)为频率成形脉冲，LREC（矩形脉冲）的表达式为：

当M=2，h=0.5，L=1 时，采用矩形脉冲，对应常见的MSK 调制［7］。MSK 调制作为CPM 调制中的典型调制方式，在实际应用中十分广泛。矩形成形脉冲幅度不变，其对应的相位响应脉冲均匀变化。

矩形调制脉冲形状如图1 所示。

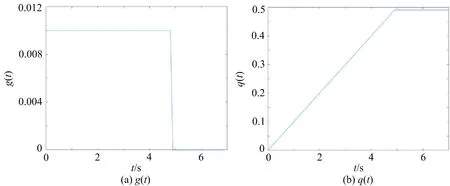
图1 矩形脉冲

其相位变化为：

因此相位状态为：

受矩形脉冲的形状限制，MSK 调制的相位改变会出现曲线折断的情况。由矩形脉冲的相位变化图可得，每个码元相位变化 π/2，图2 为信号的相位改变网格图。

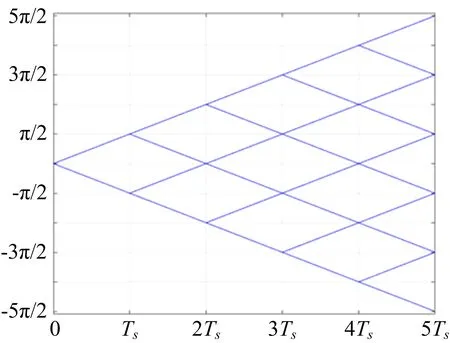
图2 MSK 调制相位改变网格

2 改进的参数联合估计算法

针对联合估计算法抗噪声性能不足、运算量大等局限，提出一种改进的联合估计算法。由于联合估计算法对剩余频偏有一定的要求，越小越好，因此载频粗估计算法较为重要。因此在原有联合估计算法的基础上，采取burg 现代谱算法，对载频进行粗估计；同时采取递进式搜索方式，在保证精度的同时，大大降低运算量。

2.1 算法原理

1） burg 现代谱载频估计算法

原载频估计方法为瞬时频率估计，误差较大，较为敏感，受噪声影响大。因此可以用功率谱法来估计载频，可以有效地抑制噪声的影响，提高参数估计的精度。burg 现代谱算法具体步骤如下：

根据前向和后向误差均方差之和最小来求取km，m阶的预测公式如下：

可得km的公式如下所示：

针对平稳随机过程，可将式（10）转换为：

Levinson 关系式如下：

而AR 模型的第m+1 个参数G为：

预测误差功率的递推关系式，如下所示：

完成以上递推关系需要知道误差功率的初始值，如下：

经过以上步骤即可得出信号的功率谱密度：

搜索信号功率谱密度峰值对信号载频进行粗估计，从而降低载频粗估计的误差。

2） 联合估计

下面考虑剩余载频fe、符号率Ts和调制指数h的联合估计问题。

为了后续分析方便，定义：

2 个区间：Ig⊂(0，2g0) 和Iα⊂(-3/(2Ts)+g0fe，3/(2Ts)+g0fe)，则由CPM 信号s(t)的循环平稳性易知，对于(g，α)∈Ig×Iᾶ，当且仅当g=g0，α=±1/(2Ts)+g0fe时：

则可以利用CPM 信号的循环平稳性对采样后的信号r[k]建立代价函数：

因此，定义搜索区间：

则fe、Ts和h的估计就可以通过对如下的代价函数进行三维搜索：

找出其最大值对应的g0、α0和β0：

则通过这三个值可以得到估计值：

3） 递进式搜索

原联合估计算法为达到较高的参数估计精度，需要使用较小的搜索间隔，每次搜索需要对所有的数据进行相关运算，所以算法的运算量比较大。因此为满足参数快速估计的需要，对代价函数的搜索进行改进，采取递进式搜索，降低运算量。

假设需要达到的精度为ε，则可以在整个搜索区间内进行较大间隔的搜索，确定包含峰值的一个较小的搜索区间，之后减小搜索间隔，满足精度的要求。具体步骤如下所示：

首先根据代价函数，对搜索区间进行粗搜索，粗搜索间隔为：

经过粗搜索后，假设代价函数最大值位置为fmax1，则缩小后的的搜索区间为：

以fmax1为中心，向前扩展一个粗搜索间隔εc，向后扩展一个粗搜索间隔εc，得到细搜索区间。之后在该区间内以要求的精度ε为搜索间隔进行搜索。

利用此方法可大大降低算法的运算量，可以达到信号参数快速估计。假设整个区间长度为d，相比原算法降低的运算量比例为：

上面只进行了2 次搜索，根据以上原理可以将搜索次数扩展为n次，将大大降低算法的运算量，同时满足精度的要求，达到参数的快速估计。

2.2 算法估计流程

图3 为上述联合估计算法的流程图。

图3 联合估计算法框图

首先通过burg 现代谱算法对信号进行载波粗估计，之后对信号进行消除载频处理。根据已知的信号情况，对搜索的参数区间范围进行限定和缩小。然后在搜索范围内，通过递进式搜索方式搜索代价函数的最大值，并提取出来，根据搜索的结果和联合估计的算法来估计信号剩余频偏和码元速率。

搜索代价函数的极大值，首先确定g的值，之后根据代价函数最大值的位置求得估计的参数，具体流程如下：

1）求JN(g，α，β)=|ξN(g，α)|2+|ξN(g，β)|2关于g的最大值max {JN(g，α，β)}；

2） 求 |ξN(g，α)|2中 关 于α的 最 大 值max {|ξN(g，α)|2}；

3） 求 |ξN(g，β)|2中 关 于β的 最 大 值max {|ξN(g，β)|2}。

完成以上步骤后，记录下对应的α、β、g的值，利用这些值根据式子计算出待估计参数的值ĥ、T̂s、f̂c。

通过上述联合估计算法的描述，该算法可以有效地一次性地估计出信号的载频、码元速率和调制指数。

3 算法仿真及性能分析

3.1 算法仿真

接下来对仿真信号进行参数估计，来验证算法的可行性。下面主要将代价函数的三维搜索转换为2 个阶段的3 次简单搜索。

仿真参数：不考虑噪声的影响，采样率fs=1 MHz，调制指数h=0.5，载频fc=100 kHz，每个码元的采样个数为25，码元速率为40 kHz。首先针对调制指数进行代价函数搜索，调制指数的代价函数图如图4 所示。

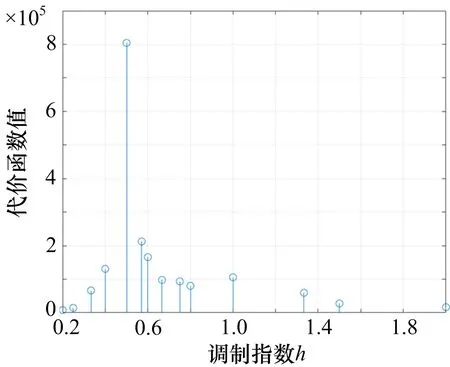
图4 不同调制指数的代价函数图

调制指数的取值为：

由于一些常用的调制指数不一定是有理数，针对调制指数的取值不采用均匀取值法。因此为降低调制指数搜索的运算量和提高调制指数估计的准确度，主要考虑常见的调制指数，搜索其代价函数。由图4可得，当调制指数为0.5 时，代价函数的值最大，与信号原始调制参数相符。

之后选取代价函数最大时的调制指数，然后根据其余2 个参数的范围进行搜索，调制指数的代价函数图如图5 所示。

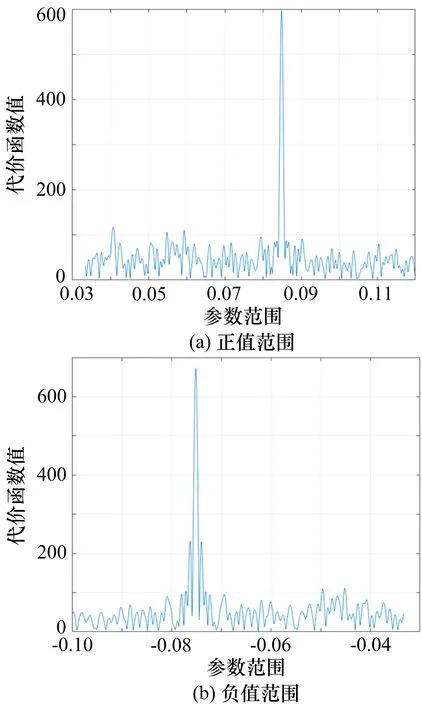
图5 代价函数随参数变化图

由图5 可得，代价函数在正值和负值范围内分别有一个最大值点，通过搜索得到峰值的参数信息，得出α、β的值，通过式（22）计算出信号载频为100 kHz 和码元速率为40 kHz，通过以上仿真过程，改进的联合估计算法可以有效估计载频、码元速率和调制指数。

3.2 性能分析

1） 载频估计算性能分析

接下来探究不同信噪比下burg 现代谱算法和瞬时频率估计算法对于载频估计的误差。仿真参数为：SNR 为-10～20 dB，码元个数300 个，采样率fs=1 MHz，调制指数h=0.5，载频fc=100 kHz，每个码元的采样个数为25，码元速率为40 kHz。通过仿真实验，由图6 可得，burg 现代谱算法可以很好地对载频进行估计，当信噪比小于9 dB 时，burg 现代谱估计的误差远小于瞬时频率估计的误差，同时当信噪比逐渐减小时，burg 现代谱算法估计的误差基本不变，展现出较强的抗噪声性能，且满足联合估计算法对于粗估计误差的要求。

图6 2 种载频估计算法误差随信噪比变化图

2） 改进后的算法整体性能分析

改变载频粗估计的算法，使用burg 频谱法减小参数估计的误差，同时采用粗搜索和细搜索方式，接下来做以下仿真实验：

仿真参数：SNR为-10～20 dB，码元个数300个，采样率fs=1 MHz，调制指数h=0.5，载频fc=100 kHz，每个码元的采样个数为25，码元速率为40 kHz。

如图7 所示，当信噪比较小时信号误差相比于粗估计采用瞬时频率法时显著减小。同时在载频估计基本准确的情况下，载频估计的抗噪声性能显著提高，对信噪比要求降低了8 dB。

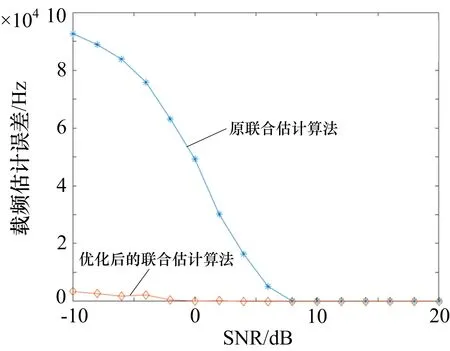
图7 载频估计误差随信噪比变化图

如图8 所示， 当信噪比较小时信号误差相比于粗估计采用瞬时频率法时显著减小。同时在码元速率估计基本准确的情况下，码元速率估计的抗噪声性能显著提高，对信噪比要求降低了8 dB。

图8 码元速率估计误差随信噪比变化图

在保证精确度的情况下采用递进式搜索，粗搜索采用原有精度的0.1 进行估计，细搜索采用原有的精度估计。图9 为仿真结果。

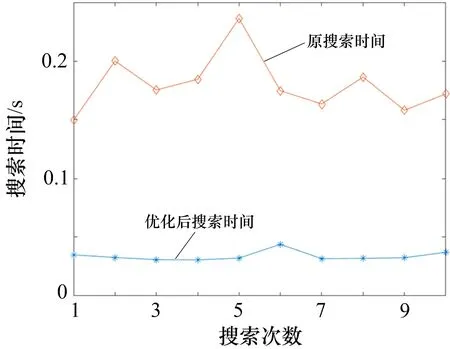
图9 2 种搜索方式的搜索时间

通过计算，原始搜索方式进行一次参数估计的平均时间约为0.18 s，改进后进行一次参数估计的平均时间约为0.033 8 s，整个运算时间节省了80%左右，可以显著看出参数估计的运算量显著减少，有利于参数的快速估计。

综上所述，改进后的联合估计算法在信噪比较小时，参数估计的误差显著降低，同时抗噪声性能显著提高。通过采用递进式搜索显著降低算法的运算量，达到快速估计的目的。

4 结束语

本文通过研究MSK 信号的符号周期、调制指数和载波频率等参数的估计算法，针对联合估计算法的局限性，提出一种改进的MSK 参数联合估计算法。该算法可以在低信噪比条件下快速进行参数估计，为通信侦察对抗和情报获取提供技术支撑，对电子对抗侦察具有重要意义。■