贝叶斯优化TQWT 参数在轴承故障诊断中的应用

张乐，彭先龙，朱华双

（西安科技大学 机械工程学院，西安 710054）

轴承是旋转机械的核心部件，研究早期故障信号特征，识别故障类型，采取合理的应对措施，对维护设备安全稳定运行十分重要。

可调品质因子小波变换（Tunable Q-factor wavelet transform，TQWT）是Selesnick 提出的一种参数可控可调节的过完备小波变换[1]，在机械故障诊断中得到广泛应用。其优点是通过调节品质因子Q、冗余度r和分解层数J这3 个关键参数，可以灵活地构造小波基函数，匹配求解旋转机械振动信号中存在的周期性冲击特征。为了合理地确定（Q、r、J）参数，孔运等[2]利用故障特征评价指标，以提升子带信号故障特征显著性为目标，遍历搜索参数组成空间，通过检测和整合不同参数组合条件下故障特征指标变化趋势，确定合理参数，构造自适应可调品质因子小波。由于三元参数存在庞大的候选组合，为提高网格搜索执行的效率，贺王鹏等[3]以（Q,r）为小波基函数自适应性调控主导参数，构建网格搜索空间。任学平等[4]在分析已有研究结果的基础上，通过调节（Q,J）参数组合获得信号最佳分解效果。合理优化搜索空间提高了可用参数的搜索效率。

应用优化算法在故障特征指标导引下实现参数自动寻优是目前研究的方向，已在变分模态分解关键参数自适应优化研究方面，取得了大量研究成果。例如：唐贵基等[5]采用粒子群算法以包络熵为优化目标，获得分解个数k和惩罚参数α最优解。刘嘉敏等[6]提出应用遗传算法对目标函数在解空间进行全局并行随机搜索，求取二元参数（k,α）最佳组合。王振亚等[7]以最小包络均熵为优化目标，用樽海鞘群算法实现变分模态分解的参数寻优。通过网格搜索和优化算法实现参数寻优，需要依靠评估函数分析某样本参数下，故障信号TQWT 分解获得子带的故障特征显著性。因评估函数无法用简单函数表示，所以样本参数评估代价大，在分析TQWT 三元参数时，遍历样本会耗费大量的计算资源。因此，寻找高效的优化算法是十分必要的。

贝叶斯优化是一种基于概率代理模型的序贯优化，可以有效地利用历史观测信息主动选择评估点，减少寻优迭代次数[8-10]，适用于求解存在观测噪音、多峰、非凸、黑箱及评估代价高等问题的优化目标，广泛用于机器学习和深度学习超参数优化[11-12]。本文针对网格搜索和算法优化实现TQWT 调参过程中目标函数评估代价高的问题，提出基于贝叶斯优化TQWT 参数的故障诊断算法，以平均香农熵和峭度联合建立故障特征评价指标，在故障特征指标导引下提取最显著故障特征子带信号，经TQWT 逆变换后由重构信号包络谱判别轴承故障类型。

1 可调品质因子小波变换（TQWT）

TQWT 采用单位离散傅里叶变换求得输入信号的频域表示，经由一系列高、低通滤波器，不断对低尺度滤波器的输出进行双通道迭代分解，获得多尺度小波系数序列，其低、高通滤波器频响函数H0（ω）和H1（ω）定义为：

式中：α为低通尺度变换系数；β为高通尺度变换系数；θ（ω）为函数过渡区间设计函数。

具有2 阶消失矩的德比契斯（Daubechies）频率响应函数可定义为

可以证明θ（ω） 在过渡频带上满足

则低、高通滤波器频响函数H0（ω）和H1（ω）在各自通带和过渡带上满足如下关系

且为了保证完美重构，α与β应满足

尺度内滤波器参数（α,β）可由TQWT 品质因子Q和冗余度r确定[2]，即

因此，TQWT 多尺度分解与重构由三元参数（Q，r，J）决定，其中J为分解层数。为了节约算力，同时避免过渡分解导致的频带信息冗余，分解层数J存在理论上限Jmax，计算公式为

式中：N为待分析信号长度；“”为向下取整运算符。

2 贝叶斯优化TQWT 参数

TQWT 算法匹配故障特征构造可调品质因子小波，可以看作一个优化问题，即

式中：x为一个三维决策向量，由TQWT 算法预设参数（Q,r,J）定义x的决策空间Ω；xbest是最优参数设计，f（·）为优化目标函数。如优化目标为最大化问题，可对目标函数取负号转化求解。

2.1 概率代理模型

贝叶斯优化通常采用高斯过程建立非参数模型。以目标函数f（x）评估TQWT 在某参数x下分解信号所得子带故障特征的显著性，会得到确定的计算值。为满足高斯过程条件，在目标函数f（x）计算中添加观察噪声得到观察值

式中ε为观察误差，ε～N（0,σ2）。

目标函数f（x）作为观察对象，其对应的观察值y为服从正态分布的随机变量，则“观察”某参数条件下 TQWT 子带故障特征成为具有一定成功概率的独立事件，满足高斯过程，可通过概率模型估计目标函数f（x），即

式中：GP为高斯分布；m（x） 为均值函数，m（x）=E[f（x）]；k（x,x'）为协方差函数,k（x,x'）=E{[f（x）-m（x）][f（x'）-m（x'）]}。

由高斯过程性质推导可得概率代理模型预测公式为

2.2 基于预期改进的采集函数

当决策空间进行了n次采样，目标函数最小值的改进量定义为

新观察位置x应满足目标函数f（x）改进量I（x）取最大值，即

在选择下一观察位置之前，新位置的目标函数值未知，可由历史观察数集y, 根据f（x）后验分布估计预期的提升量EIn（x）（Expected improvement，EI），则式（15）更新为

式中En[·]为函数f（x）在已给定的n次采样下所得后验分布的期望。

由式（12）可知f（x）后验分布服从均值为µ(x)和方差为σ2(x)的正态分布，求得期望[13]为

式中：Δn(x)为目标函数在点x的历史最优值与期望值之间的差值，Δn(x)=-µ(x) ； Φ(·)为标准正态分布的累积函数；φ(·)为标准正态分布的概率密度函数。使用1 阶或2 阶优化算法可以求解式（17）中满足式（16）预期改进量EIn（x）最大化的解，即新的“潜在”观察评估点。

2.3 优化目标函数

贝叶斯优化TQWT 参数需要有效的故障特征导引。峭度对信号振动变化十分敏感，能反映信号中蕴含的冲击特征，其值越大信号的冲击特征就越显著，广泛用于显著故障特征子带抽取[14-15]，定义为

香农熵可以用于故障特征评价，振动信号周期性越明显，熵值越低；噪声干扰越多，熵值越大[16]，但是TQWT 分解所得小波系数序列的长度不同，经典香农熵无法评估此类小波系数序列，可采用平均香农熵，即:

在参考已有综合特征指标建立方法的基础上，本文以平均香农熵与峭度之比定义熵-峭指标，评价信号的故障特征显著性，其定义为

式中：Ej和Kurtj分别为尺度j下子带信号对应的平均香农熵和峭度。由熵-峭指标EK定义可知，EK值越小，冲击特征越显著，据此建立的综合目标函数为

式中：x为TQWT 三元参数（Q,r,J）定义的决策向量；EK（x）j为参数x作用下尺度j子带信号熵-峭指标计算值。目标函数f（x）以多尺度子带熵-峭指标最小值评估当前参数组合x的性能。

贝叶斯优化TQWT 参数的流程如图1 所示。

图1 贝叶斯优化过程Fig.1 Bayesian optimization process

具体步骤如下：

步骤1 根据TQWT 算法三元参数（Q,r,J）取值范围初始化参数集X={x1,x2, ···,xn}，由式（10）和式（22）得到X对应的故障特征观测数据集y={y1,y2, ···,yn}。

步骤2 根据式（12）更新目标函数f（x）高斯代理模型。

步骤3 根据式（16）求解满足采集函数EIn（x）最大化的下一“潜在”观察目标位置xnew。

步骤4 由式（10）和式（22）计算新观察点xnew观察值ynew，加入历史观测数据集。若新点xnew目标函数值f（xnew）取得最小值，则更新当前最优位置xbest=xnew。

步骤5 重复执行步骤2 ～ 步骤4，循环迭代指定次数，输出最优位置xbest。

与粒子群优化、遗传算法等进化方法相比，贝叶斯优化算法可以显著提高优化求解效率，降低计算资源消耗。进化方法在迭代过程中需要更新种群内部全体或部分粒子（个体）。如文献[5]中粒子群优化通过迭代更新每个粒子的速度和位置搜索参数组合空间。文献[16] 中遗传算法采用单点交叉和变异，每代中有1/4 的个体被淘汰。粒子（个体）每次更新后都要重新计算对应的适应度值，而评估更新粒子（个体）的适应度值会耗费一定的计算资源，当种群规模扩大时会影响算法的分析性能。

贝叶斯优化算法更新采样点的策略与进化方法不同，在迭代过程中根据概率代理模型，将采集函数预期改进最优的位置作为下一观察点，提高了趋向目标函数极值更新参数的准确性，且每次迭代只需评估一个新位置的目标函数值，减少了算法耗费的计算资源。通过初始观察数据集建立的概率统计模型随迭代会不断更新，提高预测“潜在”观察位置的准确性， 使优化目标函数快速收敛稳定，可在更新少量样本的条件下求得可用的优化参数解。

3 仿真信号分析

为验证贝叶斯优化算法利用本文熵-峭指标优化TQWT 参数提取轴承故障特征的有效性，模拟构建一组含噪周期冲击信号。仿真信号由周期冲击信号、谐振干扰和背景噪声叠加构成，可以表示为

式中：I（t）为冲击振动信号；h（t）为系统谐振干扰；n（t）为工作背景噪音。

仿真信号及各组成成分如图2 所示，其采样频率为12 kHz，采样点数12 000 点。

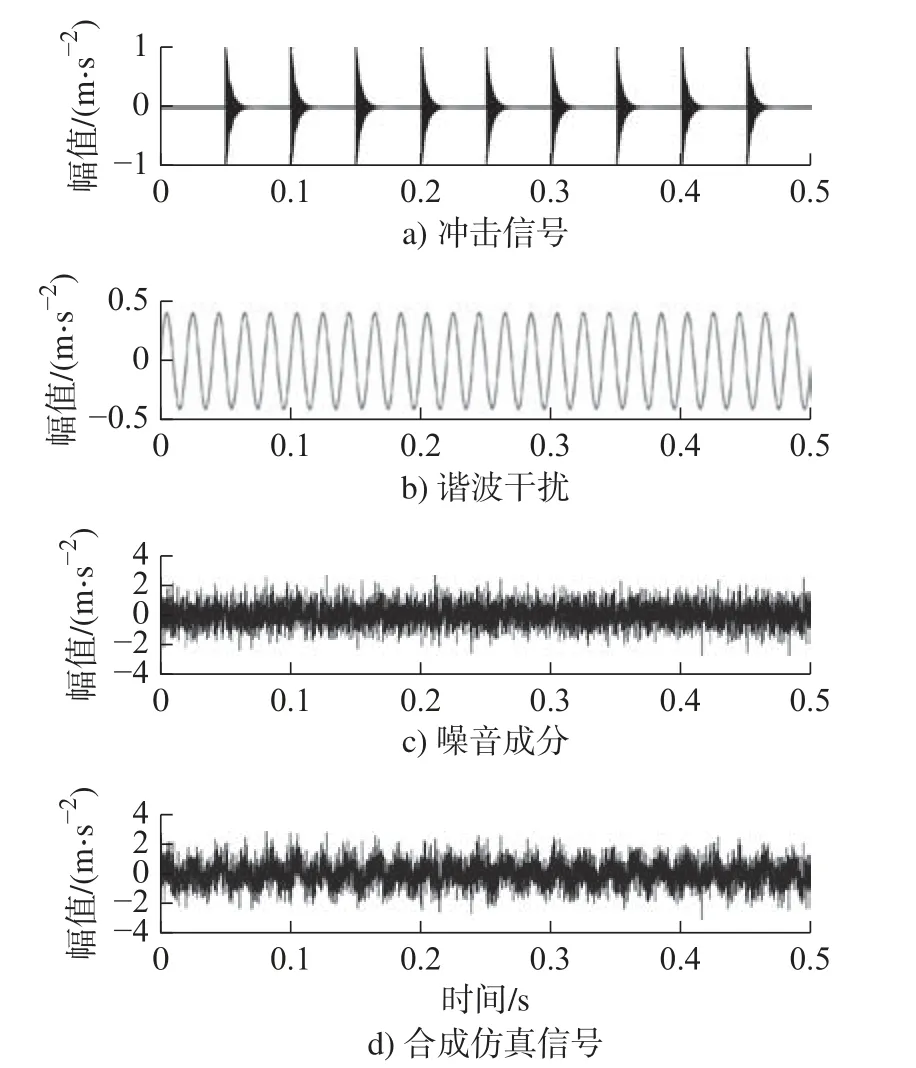
图2 仿真信号时域波形及组成成分Fig.2 Time domain waveform and components of simulated signals

各组成部分如下：

1）周期性冲击振动信号I（t），由单点冲击信号延时叠加构成，即

式中： ζ为阻尼系数，ζ=0.02 ； ω为系统共振频率，ω=2πfn，fn=2 000 Hz；A为振动的幅值，A=1.2；T为冲击周期，T=0.05 s。

2）谐波干扰信号h（t）频率为50 Hz，则

3）背景噪音n（t）选择服从均值μ为0，方差σ为0.6 的高斯白噪声。合成仿真信号噪比为-13 dB。从图2 中可以看出，合成仿真信号受到谐振和噪声的严重污染，已无法直接观察振动信号的变化规律。原信号所含周期性冲击特征在图3 包络谱中无法有效识别。应用贝叶斯优化算法优化TQWT参数，设置品质因子和冗余度的初始值QL和rL均为2，上限QU和冗余度rU分别为8 和6。分解层数的初始值JL为5，对应上限JU根据最大分解层数公式（8）确定，由QL和rL计算得到JU为17。后续实验采用相同设置，如需要增大分解层数上限，需要匹配增大品质因子Q和冗余度r的下限值。

图3 仿真信号Hilbert 包络谱Fig.3 Hilbert envelope spectrum of simulated signal

根据图1 所示的贝叶斯优化算法执行100 次迭代计算，目标函数值变化过程如图4 所示，在40 次迭代运算后趋于稳定，得到TQWT 参数组合为（Q= 7,r= 2,J= 13）。利用文献[2]TQWT 滤波算法分解仿真信号，以本文熵-峭指标评估TQWT 分解获得子带信号故障特征的显著性，结果如图5 中熵-峭指标计算值变化曲线所示，确定的最显著故障特征子带编号j=8（最小值）。

图4 目标函数变化过程Fig.4 Objective function variation processes

图5 最显著特征子带选择结果Fig.5 The most significant feature subband selection results

选择最显著故障特征子带进行单支重构，得到的故障特征信号波形如图6 所示，图7 为其包络谱。比较图6 中故障特征信号与原始冲击信号，可以明显观察到周期为0.05 s 的冲击特征。图7 包络谱中可以清晰辨认冲击故障特征频率1 倍频（实际19.7 Hz）及高倍频成分。图7 中：“f”为曲线对应的理论故障特征频率，“1f”为1 倍频，“2f”为2 倍频，其余及后续图示采用相同标记。因此，通过贝叶斯优化算法合理确定TQWT 参数，在熵-峭指标导引下，选择最显著特征子带信号重构后进行包络谱分析，可以成功识别噪声混叠状态下的周期性冲击特征。

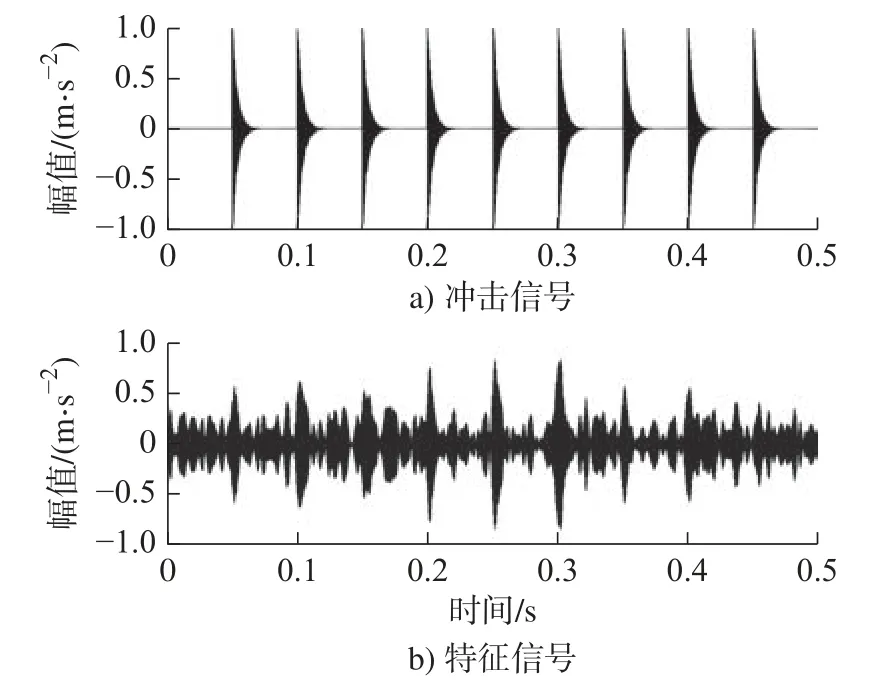
图6 提取故障特征时域波形与原冲击特征对比Fig.6 Comparison of extracted fault characteristic time domain waveform with original impact characteristics

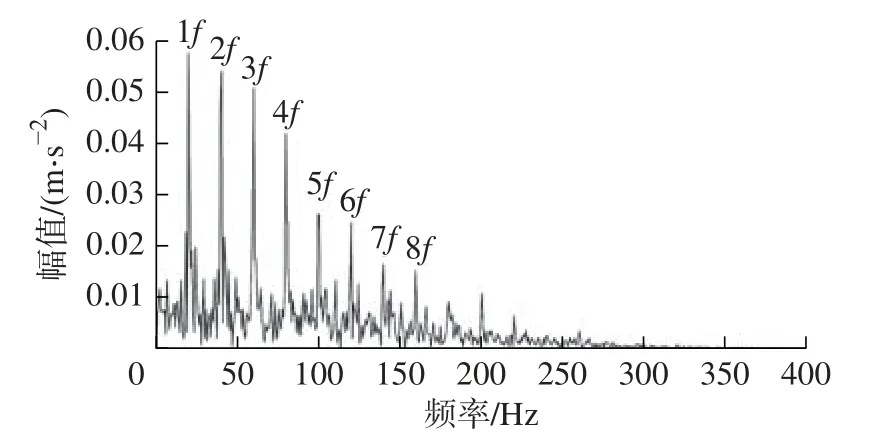
图7 提取故障特征Hilbert 包络谱（f=20 Hz）Fig.7 Extracting Hilbert envelope spectrum of fault characteristics (f=20 Hz)

4 实测故障信号分析

4.1 轴承故障信号分析

为验证本方法分析实测机械故障振动信号的有效性，采用美国凯斯西储大学（CWRU）滚子轴承故障检测数据进行验证。轴承型号6 205-2RS JEM SKF 深沟球轴承，电火花加工模拟单点故障直径为0.177 8 mm，深度0.279 4 mm，电机转速1 791 r/min（转频fr=30 Hz），采样频率fs=12 000 Hz，数据文件编号IR007_0（内圈故障），其故障信号时域波形如图8 所示。

图8 轴承故障信号时域波形Fig.8 Time domain waveform of bearing fault signal轴承内圈和外圈故障特征频率[17]计算公式为：

式中：Z为滚珠个数；d为滚珠直径；D为轴承滚道节径；α为轴承接触角，深沟球轴承为0°；fin和fout分别为轴承内圈和外圈故障特征频率；fr为轴承内外圈相对转频。查阅轴承结构参数，根据式（26）可以得到对应内圈故障特征频率fin=162.2 Hz。

从图8 原始振动信号时域波形可以看出信号波形变化复杂，含有大量的噪声干扰。采用本文贝叶斯优化算法，经过图9 所示的100 次迭代计算求得TQWT 参数组合为（Q=6,r=4,J=15）。

图9 目标函数变化过程Fig.9 Objective function variation process of inner ring fault signals

利用熵-峭指标评估TQWT 分解获得子带信号故障特征的显著性，结果如图10 所示。确定最显著故障特征子带编号j=4，由TQWT 逆变换进行单支重构获得降噪特征信号及其包络谱，如图11 所示。

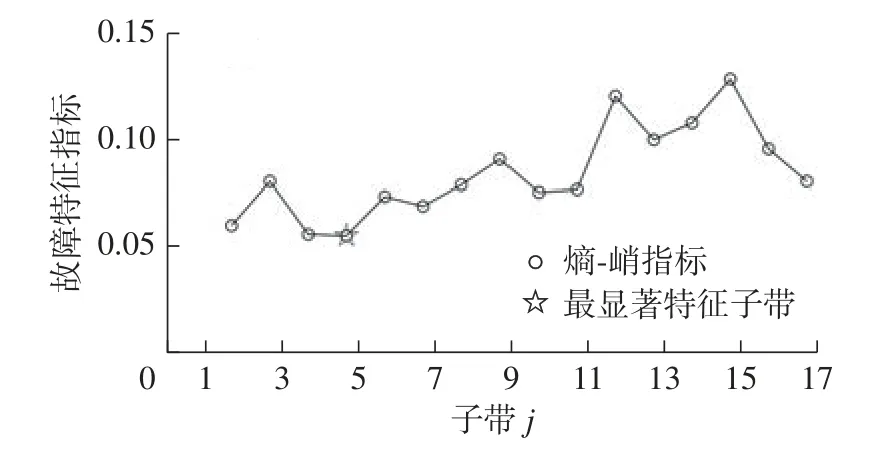
图10 最显著特征子带选择结果Fig.10 The most significant feature subband selection results of inner ring fault signals

图11 故障特征提取结果Fig.11 Fault feature extraction results of inner ring fault signals

将图8 原始故障信号和图11a）提取故障特征信号时域波形相比较，可知算法降噪效果良好，提取特征信号的周期性冲击特征显著。分析图11b）特征信号包络谱可以准确获得故障特征频率1 倍频（实际161.9 Hz）及其2 倍频和3 倍频，还可以观察转频fr（实际30.0 Hz）。试验结果与理论分析结果一致，揭示了原故障信号中包含的周期性冲击特征，据此可准确识别轴承故障类型。

4.2 全寿命信号早期故障分析

为验证贝叶斯优化TQWT 滤波算法与熵-峭指标提取早期轴承故障所含微弱冲击特征的能力，对NSF I/UCR智能维护系统中心（IMS）滚动轴承实验数据进行了分析研究。IMS 轴承数据共记录了3 组滚动轴承全寿命振动加速度信号，选择第2 组1 号轴承实验数据（外圈故障），位置如图12 所示。轴承型号ZA-2115，采样频率fs= 20 000 Hz，采样间隔10 min，持续时间164 h，共采集数据文件984 个，每个文件长度为20 480 个采样点，电机转速2 000 r/min（转频fr= 33 Hz）。查阅轴承结构参数，根据式（27）得到此轴承外圈故障特征频率fout= 235.3 Hz。

振动信号均方根值的变化趋势可以反映轴承的工作状态。图13 为1 号轴承在全寿命工作过程中均方根值的变化。从图中可以看出，轴承在5 000 min之前运行稳定，到5 200 min 后均方根值开始逐渐增大，约至7 000 min 时发生突变，标志轴承状态发生改变，7 000 ～ 9 000 min 时段均方根值波动上升，运行9 000 min 后均方根值开始大幅增加，在9 800 min时取得最大值，轴承寿命达到极限。试验选择分析3 600 min 时刻振动数据，此时故障仍处于潜伏发展阶段，故障信号包络谱分析无法直接有效提取振动数据中可能存在的故障特征[5]。

图13 1 号轴承振动信号均方根值变化趋势Fig.13 Root mean square (RMS) value variation trend of vibration signals of bearing 1

为了准确提取早期故障中存在微弱振动信号，采用本文贝叶斯优化算法，执行500 次迭代运算，确定的TQWT 参数组合为（Q=3,r=6,J=11），如图14所示。

图14 目标函数变化过程Fig.14 Objective function variation process of outer ring fault signals

利用熵-峭指标评估TQWT 分解子带信号故障特征的显著性，结果如图15 所示，确定最显著故障特征子带编号j=1，通过单支重构获得的故障特征信号及其包络谱如图16 所示。由图16a） 可以发现提取故障特征信号时域波形的冲击特征变化具有较强的规律性，在图16b）包络谱中可以准确获得其故障特征频率主频峰值点（实际231.0 Hz）。理论分析与实验分析结果一致，但是倍频特性与其他频率成分混杂，无法清晰辨识，所得的主频峰值点可作为早期故障预判的支撑数据。

图15 最显著特征子带选择结果Fig.15 The most significant feature subband selection results of outer ring fault signals

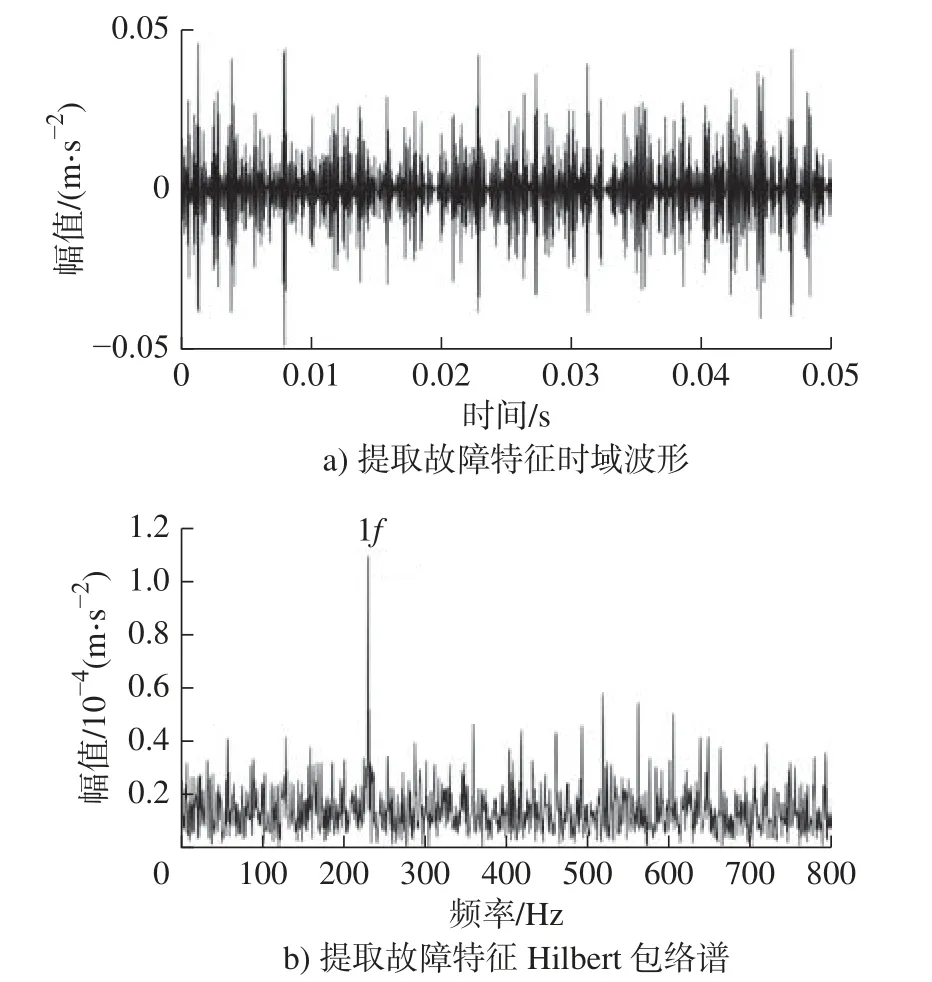
图16 故障特征提取结果（f = 235 Hz）Fig.16 Fault feature extraction results of outer ring (f = 235 Hz)

应用本文贝叶斯优化算法，分别以平均香农熵和峭度建立优化目标函数，分析相同时刻（3 600 min）轴承振动数据，执行500 次迭代求取合理设置参数，在独立特征指标导引下分析早期故障特征，如图17a）和图18a）所示。

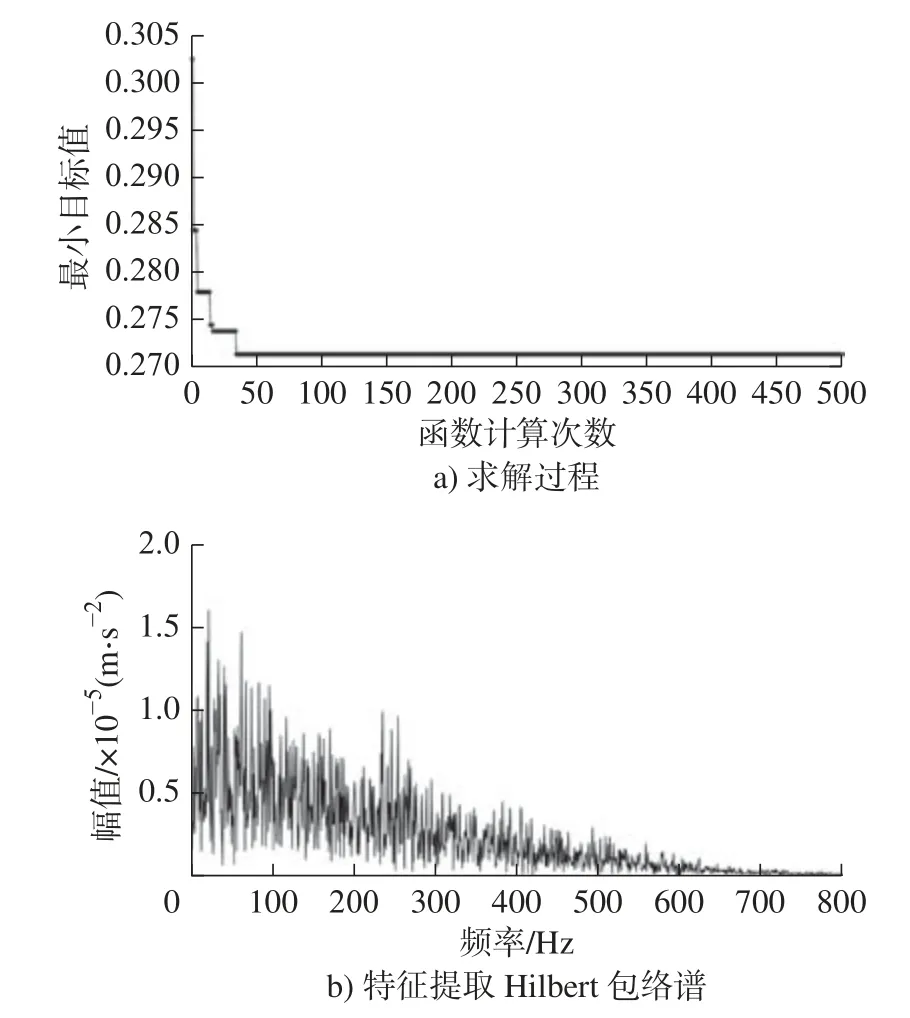
图17 以平均香农熵为目标函数提取故障特征Fig.17 Utilizing average Shannon entropy as objective function for fault feature extraction

图18 以峭度为目标函数提取故障特征Fig.18 Extracting fault features with kurtosis as objective function

以平均香农熵作为优化目标得到的TQWT 参数组合为（Q=7,r=6,J=12），其对应最显著特征子带编号j= 11。当以峭度作为优化目标时，因子带信号故障特征对应峭度最大值，在算法求解时需要取负号建立目标函数，得到的TQWT 参数组合为（Q=8,r=6,J=16），其对应最显著特征子带编号j= 13。分别选择两种目标函数对应的最显著特征子带进行单支重构，获得对应故障特征信号的包络谱如图17b）和图18b）所示，从包络谱图中无法定位轴承故障特征频率及其他相关频率信息。因此，基于平均香农熵和峭度分别建立目标函数，无法有效提取轴承早期故障特征，熵-峭指标对早期轴承故障特征的适应性优于独立特征评价指标。

5 结论

贝叶斯优化算法近些年在多领域研究中得到广泛应用，本文将贝叶斯优化算法与可调品质因子小波变换（TQWT）相结合，提出一种基于贝叶斯优化TQWT 参数的故障诊断算法，得到以下结论：

1）贝叶斯优化算法通过概率代理模型和采集函数提高了样本迭代更新的效率，在更新少量样本的条件下目标函数值快速收敛稳定，降低了算法执行过程中样本总体的评估代价。

2）本文以平均香农熵与峭度之比定义熵-峭指标，评估信号故障特征显著性，在小波变换域上可准确识别最显著故障特征子带。实测信号分析表明熵-峭指标对早期故障特征的适应性优于独立评价指标。

3）综合仿真实验与实测轴承振动信号分析结果表明，利用贝叶斯优化TQWT 参数，采用熵-峭指标引导最显著故障特征子带选择，可以提取轴承早期故障中存在的微弱故障特征，为故障诊断和早期预警提供有价值的支撑数据。