循环冲击激励下某发动机附件传动系统的振动特性研究

严红，刘正强，蒋沁辰，任鸿飞

（1.中国航发南方工业有限公司，湖南 株洲 412002；2.空装驻株洲地区军事代表室，湖南 株洲 412002；3.西北工业大学 机电学院，西安 710072）

航空发动机附件传动系统作为飞行器的重要组成部分之一，为避免飞行过程中因发动机产生的振动导致重大事故的发生，因此要求发动机内部的附件传动系统具有高稳定性及可靠性。

作为齿轮耦合复杂转子系统的附件传动系统[1]，各转子之间因齿轮副的啮合作用发生弯曲、扭转和摆动振动的相互耦合，故需针对具体附件传动系统建立相应的弯扭轴摆耦合动力学模型，根据求解得到的系统动态特性对附件传动系统进行改进。研究表明：齿轮的耦合作用会对整个转子系统的振动特性产生重大影响。郜雪鹏等[1]和丁仁亮等[2]基于轴单元法对附件传动系统进行固有模态分析，发现系统会派生出新的弯扭耦合模态。卢艳辉等[3]基于有限元素法对某型航发附件传动系统齿轮副进行振动特性分析，为分析其他类型系统提供参考。孙小庆等[4]基于ADAMS 软件对某型垂直升船机传动系统进行动力学仿真，获得弯曲应力载荷分布曲线，并预测齿轮疲劳寿命。欧阳旭靖等[5]提出了一种确定复杂传动系统危险齿轮的方法，为系统故障诊断提供参考。江平等[6]通过研究高速下齿轮辐板的动应力测试技术，发现实际工况下齿轮副主要以1、3 阶振型进行振动，基于此对辐板进行改进，降低辐板动应力。姜景明等[7]运用图论知识、路径规划算法和广探法等，提出了一种针对平行轴传动系统方案设计的智能化方法。吕胜[8]基于MASTA 软件分析某型附件传动系统动力学特性，并与实验对比验证了MASTA 软件在进行传动系统动力学分析方面的可行性。陈卓[9-10]以一典型发动机附件传动系统为例建立动力学模型，研究了冲击响应下的动力学行为。Kahraman[11]和Kubur 等[12]对多啮合斜齿轮系的动力学行为进行了研究，确定出不同载荷条件下的齿轮啮合相位，预测固有振型的同时，对螺旋角和加载条件对固有振型的影响进行阐述，最终得到由于静传动误差激励而产生的强迫响应。

在某涡桨发动机中，整个附件传动系统依靠一对弧齿锥齿轮传动与发动机高压转子系统相联，形成一个多转子-齿轮-轴承耦合复杂系统，在该系统中，由于各转子轴线位置、齿轮类型和轴承数量等都不相同，因此其动力学分析十分复杂。为了解决该涡桨发动机中附件传动系统动力学建模困难的问题，本文基于子结构总体耦合矩阵法，将同轴多转子耦合系统和斜交弧齿锥齿轮耦合多转子子系统的动力学模型加以综合和扩展，建立了中央传动锥齿轮副、第一级传动锥齿轮副和第二级传动圆柱齿轮副所组成的附件传动系统弯-扭-轴耦合动力学模型（方程），使用变阶次Adams-Bashforth-MoutlonPECE算法对动力学方程进行求解，获得不同循环冲击载荷谱下系统的动态响应，研究了该发动机附件传动系统的动力学行为。

1 某发动机附件传动系统动力学模型及方程

某发动机附件传动系统的运动简图如图1 所示。由图1 可知：动力由涡轮转子引出，通过花键传递给中央主动弧齿锥齿轮1，中央从动弧齿锥齿轮2与第二级主动弧齿锥齿轮3 共轴，第二级从动弧齿锥齿轮4 与第三级的主动斜齿圆柱齿轮5 共轴，第三级的从动斜齿圆柱齿轮6 与起动发电机相联。该附件传动系统共有3 对齿轮副和4 根转轴。根据下斜附件传动系统的结构，将编号为1 ～6 的各运动构件等效为具有质量和转动惯量的节点，各个节点通过具有刚度和阻尼的弹簧进行连接[13]；将相邻两节点之间的传动轴段单元视为无质量,但是具有弯曲、扭转和轴向刚度的弹簧和阻尼器；各级齿轮副的啮合关系等效为沿啮合线方向的弹簧和阻尼;根据以上处理原则建立下斜附件传动系统的弯扭轴耦合动力学模型如图2 所示。

图1 某航空发动机附件传动系统的运动简图Fig.1 Motion of an aero-engine accessory transmission system

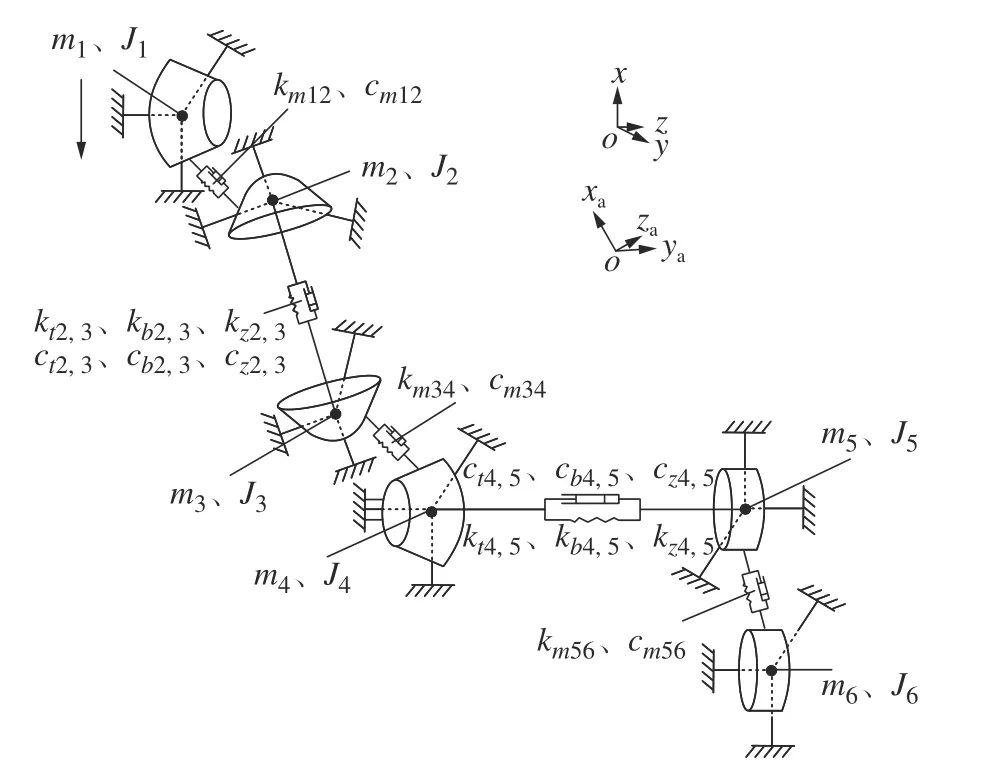
图2 某航空发动机附件传动系统的动力学模型Fig.2 Dynamic model of an aero-engine accessory transmission system

首先建立一个整体坐标系，该坐标系原点位于斜传中主动锥齿轮的锥顶，轴与斜传中主动锥齿轮中心轴线重合，轴与斜传中被动锥齿轮中心轴线重合，由于锥齿轮副轴交角并非，因此建立辅助坐标系，其中轴与斜传中被动锥齿轮中心轴线重合，轴沿啮合点切向方向，轴沿啮合点径向方向。由于本文侧重于锥齿轮传动，且由于弧齿锥齿轮的啮合特性，除了具有绕中心轴的扭矩，其径向和轴向的载荷也较大，因此附件传动系统中的弧齿锥齿轮都具有4 个自由度，即绕中心轴线转动的转动自由度（单位：rad），以及沿坐标轴方向的平移自由度（单位：m）；同理，对于斜齿轮运动构件来说，其和弧齿锥齿轮类似；这样整个改进后的附件传动系统动力学模型共具有24 个自由度。

考虑到系统包含两对非正交弧齿锥齿轮，使用相对位移法消除刚体位移无法实现，故采用输出端软弹簧固定法消除刚体位移[14]。如图3 所示，在齿轮1 上添加一个作用于扭转方向的刚度为kt1=1×102Nm/rad的弹簧，弹簧连接基座和齿轮1。

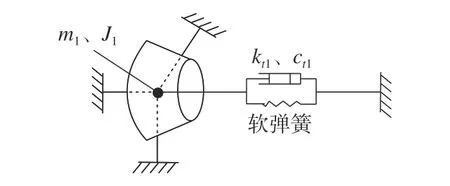
图3 软弹簧法消除刚体位移Fig.3 Soft spring method to eliminate rigid body displacement

1.1 系统动力学方程

1）中央主动锥齿轮1

2）中央从动锥齿轮2

3）第二级主动锥齿轮3

4）第二级从动锥齿轮4

5）第三级主动圆柱齿轮5

6）第三级从动圆柱齿轮6

分别建立各耦合子单元的动力学模型，推导其动力学方程，并得到各类耦合子单元的质量矩阵、刚度矩阵以及阻尼矩阵，然后对各个矩阵进行组装即可得到附件传动系统的总体质量矩阵、刚度矩阵和阻尼矩阵，即表现形式为

式中：[M] 、 [C] 、[K]分别为系统动力学方程的质量、阻尼、刚度矩阵；{X} 、{T}分别为位移和扭矩向量。

1.2 齿轮副耦合方程

规定主、从动轮各坐标方向的位移投影至啮合线方向，规定沿法向啮合力正方向的投影为负[15]。

1）中央传动锥齿轮副

法向动态啮合力为

啮合力分力为：

沿啮合点法向相对位移为

2）第二级传动锥齿轮副

法向动态啮合力为

啮合力分力为：

沿啮合点法向相对位移为

3）第三级传动圆柱齿轮副

法向动态啮合力为

啮合力分力为：

沿啮合点法向相对位移为

2 系统激励描述

2.1 时变啮合刚度[15]

为获得较为精确的啮合刚度，并考虑到弧齿锥齿轮啮合过程中啮合点的位置不断变化，不同啮合位置处的弹性变形量较难准确获得，故根据轮齿承载接触分析（LTCA）计算齿轮副扭转啮合刚度Kθ为

式中：Mn为主动轮扭矩； θ为主动轮弹性扭转角。

齿轮副啮合刚度K与扭转啮合刚度Kθ存在如下关系

式中r为啮合点处半径。

基于LTCA 求得一个啮合周期内各啮合点的扭转啮合刚度及啮合点半径，进一步根据式计算得啮合刚度离散值，通过傅里叶级数拟合得到齿轮副时变啮合刚度为

式中：km为平均啮合刚度；Aki为刚度第i阶谐波幅值； φki为初相位。

2.2 循环冲击载荷谱

某发动机的附件传动系统的负载为循环冲击载荷谱，图4 给出了两种典型的循环冲击载荷谱，其数学描述为

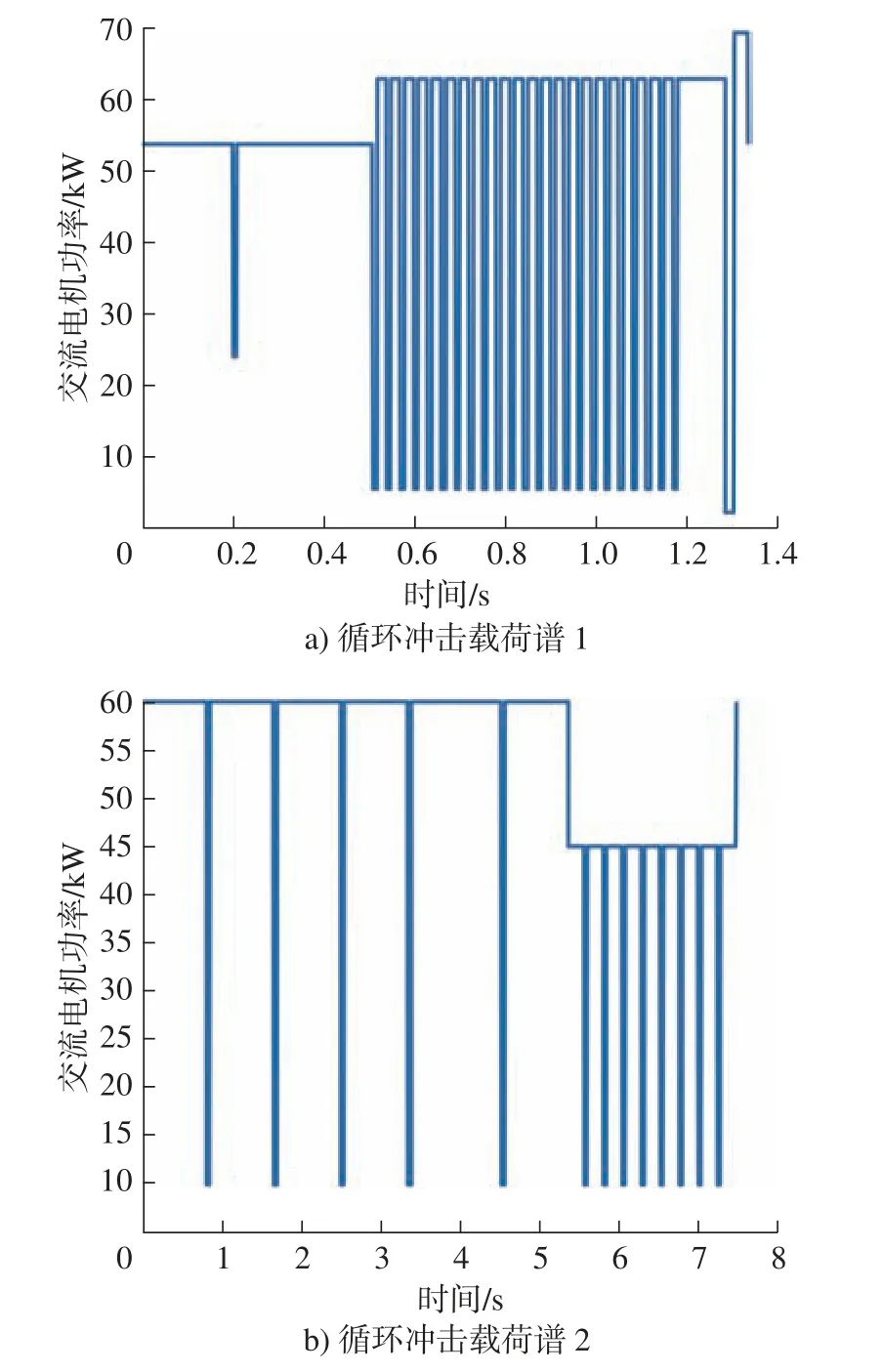
图4 循环冲击载荷谱Fig.4 Cyclic impact load spectrum

循环冲击载荷谱作为外部激励引入动力学方程（7），即可求得冲击响应。

3 数值结果及其分析

3.1 齿轮与轴段参数

该附件传动系统中各齿轮的基本几何参数如表1 所示，具体系统参数如表2 所示。

表1 齿轮的基本几何参数Tab.1 Basic geometric parameters of gears

表2 系统参数Tab.2 System parameters

3.2 循环冲击载荷谱1 下振动特性

基于变阶次Adams-Bashforth-MoutlonPECE 算法求解附件传动系统动力学方程，求得系统稳态下动力学响应曲线。图5～图7 为循环冲击载荷谱1下某发动机附件传动系统各级齿轮副的法向相对位移时间历程图和动载系数时间历程图。循环冲击载荷谱1 下各级齿轮副的动载系数均值和法向振动加速度均方根如表3 所示。

表3 循环冲击载荷谱1 下结果汇总Tab.3 Summary of results under cyclic impact load spectrum 1

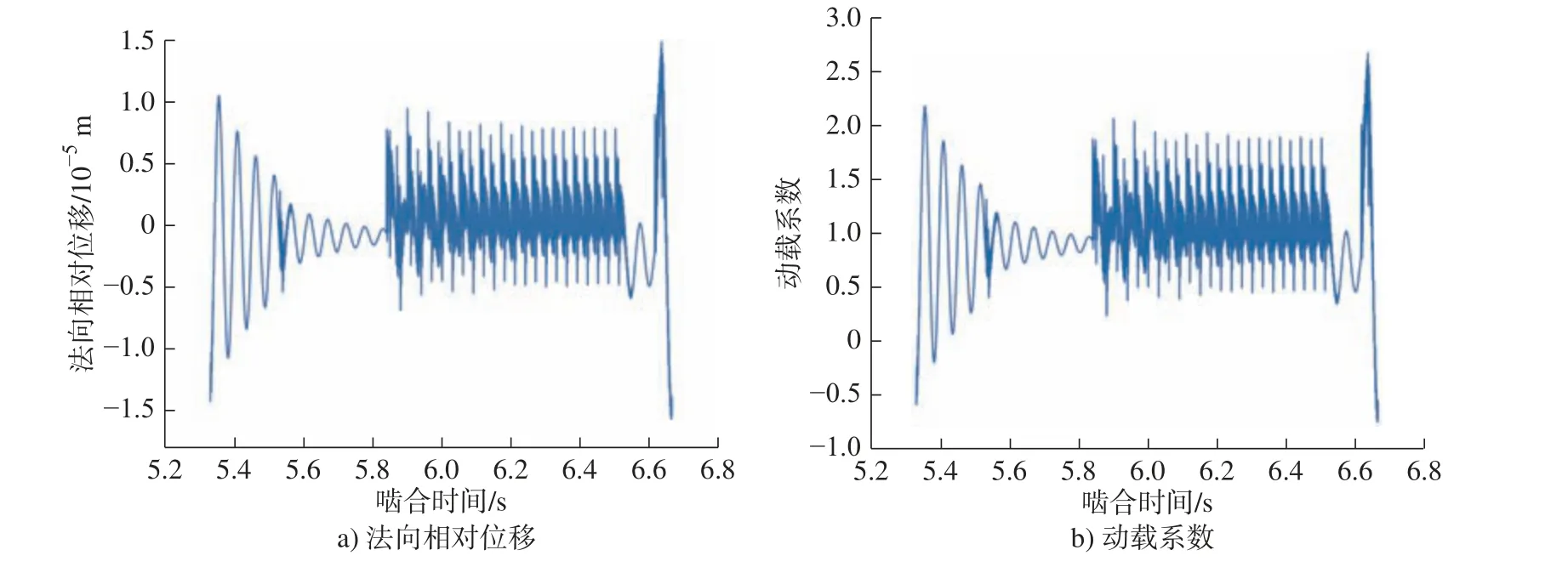
图5 载荷谱1 下中央传动锥齿轮副振动特性Fig.5 Vibration characteristics of central transmission bevel gear pair under load spectrum 1

图6 载荷谱1 下第二级传动锥齿轮副振动特性Fig.6 Vibration characteristics of the second-stage transmission bevel gear pair under load spectrum 1

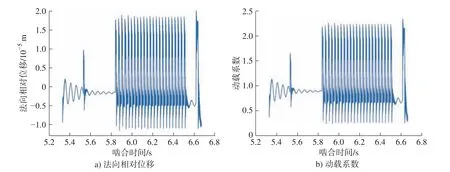
图7 载荷谱1 下第三级传动圆柱齿轮副振动特性Fig.7 Vibration characteristics of the third-stage transmission cylindrical gear pair under load spectrum 1

由图5 ～ 图7 可知：该附件传动系统各级齿轮副为周期振动，且一个负载周期中同时包含有多个啮合周期。

由表3 可知：法向相对位移最大值为0.210×10-5m，最大动载系数均值为1.000，最大法向振动加速度均方根为140.364 m/s2，三者均发生在斜传下斜齿轮副上。出现该现象的主要原因是第三级齿轮副传递的扭矩较大，且斜齿轮副的运转平稳性和承载能力不及弧齿锥齿轮副，因此产生较大的振动与冲击。

3.3 循环冲击载荷谱2 下振动特性

图8 ～ 图10 为循环冲击载荷谱2 下某发动机附件传动系统各级齿轮副的法向相对位移时间历程图和动载系数时间历程图。

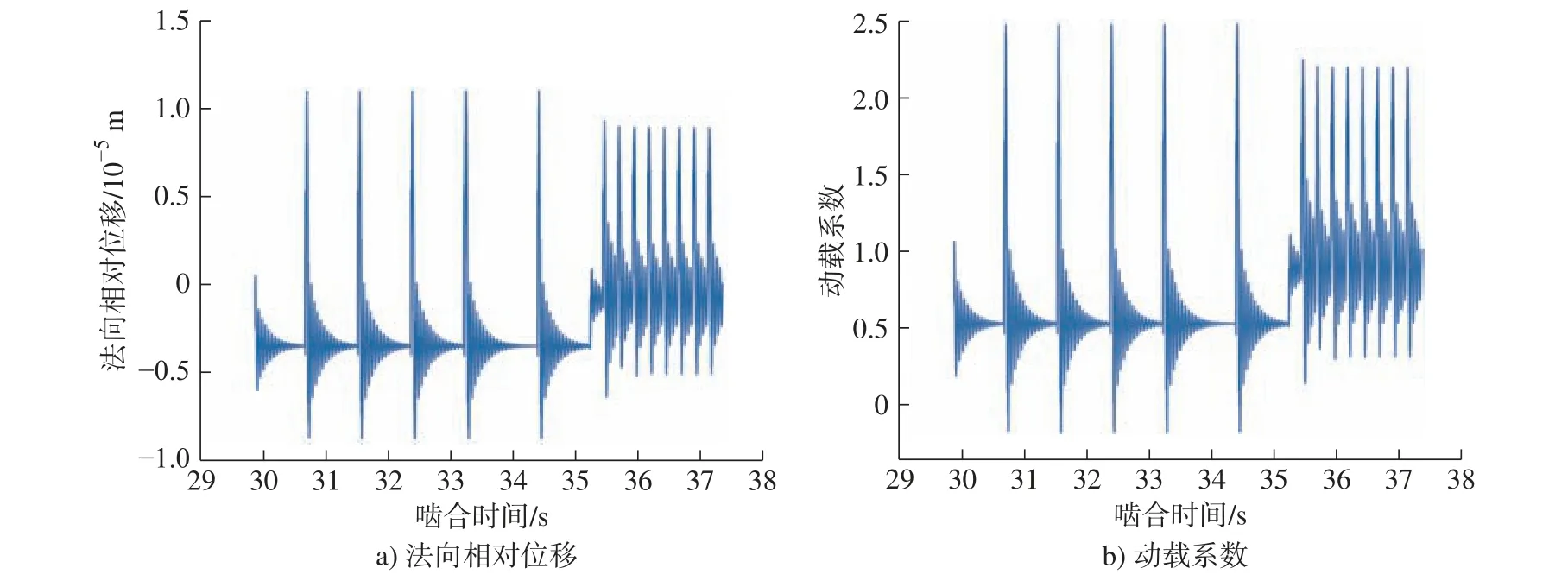
图8 载荷谱2 下中央传动锥齿轮副振动特性Fig.8 Vibration characteristics of central transmission bevel gear pair under load spectrum 2

图9 载荷谱2 下第二级传动锥齿轮副振动特性Fig.9 Vibration characteristics of the second-stage transmission bevel gear pair under load spectrum 2

图10 载荷谱2 下第三级传动圆柱齿轮副振动特性Fig.10 Vibration characteristics of the third-stage transmission cylindrical gear pair under load spectrum 2

循环冲击载荷谱2 下各级齿轮副的动载系数均值和法向振动加速度均方根如表4 所示。与循环冲击载荷谱1 情况类似，法向相对位移最大值、最大动载系数及最大法向振动加速度均方根均发生在斜传下斜齿轮副上，具体数值分别为0.139×10-5m、0.705 和27.887 m/s2。产生该现象的具体原因如前所述，符合预期结果。

表4 循环冲击载荷谱2 下结果汇总Tab.4 Summary of results under cyclic impact load spectrum 2

4 结论

1）循环冲击载荷谱1 的极差为66.97 kW，下斜附件传动系统中各级齿轮副最大动载系数为2.66；循环冲击载荷谱2 的极差为50 kW，最大动载系数为2.48。与国军标中针对发动机在突变转矩作用下启动时的冲击系数3.33 相近。

2）该下斜附件传动系统由于第三级齿轮副传递扭矩较大，同时斜齿轮副相较于弧齿锥齿轮副运转平稳性差，故两种交变载荷下各级齿轮副的最大法向相对位移、最大动载系数均值及最大法向振动加速度均方根均发生在斜传下斜齿轮副上。

3）各级齿轮副沿法线方向的振动均为周期振动，且一个负载周期中同时包含有多个啮合周期。