一类平面解析系统强退化奇点的可积性
梅世明 黄土森

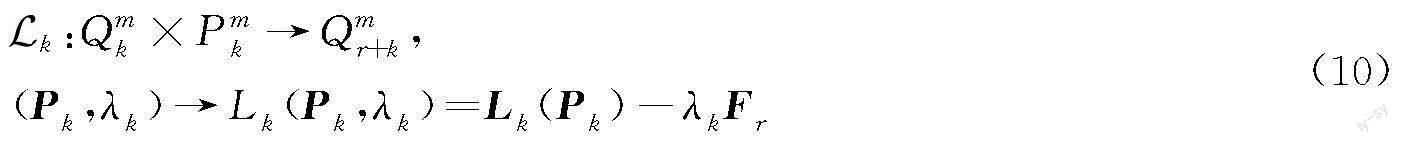
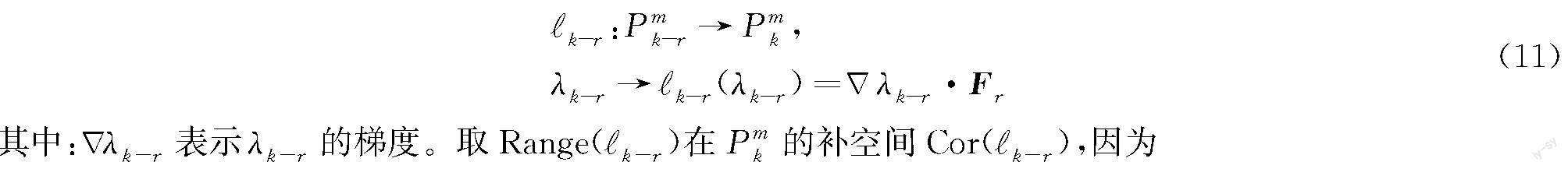
摘 要: 利用正规型理论研究一类平面解析系统强退化奇点的可积性问题。首先证明,任意一个可微系统,在可微同胚的变量变换以及时间尺度变换下,可积性保持不变。其次,对于二次齐次的微分系统,可以通过仿射变换及时间尺度变换化为4种标准形;针对其中的一种标准形,结合正规型理论,利用主系统是哈密尔顿的,且所对应的哈密尔顿函数的分解式是单因式的形式微分系统可积的充要条件,给出了相应的非线性系统可积的条件。该结果为研究平面系统的相图和局部定性结构提供了理论依据。
关键词: 平面解析系统;强退化奇点;可积性;正规型;时间尺度变换
中图分类号: O175.14
文献标志码: A
文章编号: 1673-3851 (2024) 03-0255-10
The integrability of strongly degenerate singularity for a class of planar analytical systems
Abstract: The integrability problems of strong degenerate singularities for a type of planar analytical systems are studied by means of the normal form theory. Firstly, it is proved that the integrability of any differentiable system remains unchanged under the variable transformation of the differentiable homeomorphism and time scale transformation. Secondly, the quadratic homogeneous differential system can be transformed into four canonical forms by affine transformation and time scale transformation. Finally, as for one of the canonical forms, the conditions of the integrability for the corresponding nonlinear analytical systems are given by using the normal form theory together with the necessary and sufficient conditions that the main system is Hamiltonian system and that the factorization of the corresponding Hamiltonian function only has simple factors. The results provide a theoretical basis for studying the phase diagram and local qualitative structure of planar systems.
Key words: planar analytical systems; strongly degenerate singularity; integrability; normal form; time scale transformation
0 引 言
非线性微分方程出现在应用科学的众多分支中。在平面系统的背景下,一个基本问题是单值性问题,它涉及是否可以在系统奇点的一个邻域中定义Poincar第一返回映射。如果可以定义Poincar第一返回映射,那么这样的奇点称为单值奇点[1]。对于平面解析系统而言,其单值奇点要么是一个中心,要么是一个焦点[2]。对于任一给定的系统,一旦建立了单值性,则解决Poincar的中心-焦点区分问题(通常称为中心问题或稳定性问题)的后续工作是寻找决定单值奇点是中心还是焦点的条件。
首次积分是定义在R2上的某个非空开子集上的非常数函数,它沿平面系统的解曲线(轨迹)是恒定的。对于平面系统,与中心问题密切相关的是(局部)可积性问题,即确定平面系统在单值奇点的某邻域中是否存在首次积分。如果首次积分存在,则称该平面系统是可积系统。因为首次积分的存在完全决定了一个系统的相图,所以可积性问题也是微分方程定性理论中一个非常重要的问题。平面系统的可积性类型,根据其首次积分所属的函数类不同,可以分为多项式可积、有理可积、代数可积、Ck-可积(k是自然数)、形式可积以及解析可积等。
有关确定给定平面系统是否可积的问题,与Hilbert第十六问题[3]密切相关,目前仍然是一个尚未完全解决的经典问题。如果解析平面系统的某个非退化奇点是中心,那么系统在该奇点的线性部分等价于(-y,x)T。根据Poincar定理,解析平面系统的某个非退化奇点是中心的充要条件是存在解析首次积分[2]。但当系统的奇点是退化奇点时,即系统在该奇点的线性化矩阵是幂零矩阵(相应的奇点称为幂零奇点)或零矩阵(相应的奇点称为强退化奇点或线性零奇点),虽然某些冪零中心或强退化中心有解析的首次积分,然而与非退化情形不同,此时由系统的解析可积性不能确定中心是否为幂零中心或强退化中心[3]。
变量变换是研究平面系统可积性的重要方法之一,其目的是将平面系统化为更简单的形式。对于变换后的系统,更容易确定它是否存在首次积分。正规型理论的基本思想是对平面系统进行变量变换,使用一系列近恒等变量变换及时间尺度变换(有时需要使用无穷多次[4-5]),消去系统中“不重要的项”以简化系统。通常研究简化后系统的可积性更容易些,但是只有当变换后系统的可积性与原系统的可积性一致时,才可以得到原系统的可积性,甚至求得原系统的一个首次积分。因此,变量变换的选择非常重要,在对一个系统进行变量变换时,首先就要证明所作的变量变换不会改变原系统的可积性,否则就没有任何意义。拟齐次正规型理论[4-7]是本世纪初建立起来的一个重要研究工具,它是经典正规型(即齐次正规型)理论的推广,已应用于强退化奇点的单值性与可积性等局部定性性质研究[3]。
本文主要研究一类最低次是二次齐次的平面解析系统的可积性判别条件。首先证明了在可微同胚的变量变换以及时间尺度变换下,任意一个可微系统的可积性保持不变。其次,通过仿射变换及时间尺度变换,将二次齐次的微分系统变换为4种标准形;并针对其中一种标准形,通过计算其正规型给出该类系统的解析可积条件。本文的结果有助于研究这类系统的相图和局部定性结构。
1 预备知识
考虑平面微分系统
其中:P,Q是在原点取值为零并且没有公因式的形式或解析函数,原点是系统(1)的一个孤立奇点。记X=(x,y)T,且F=(P,Q)T表示与系统(1)相关的向量场,则系统(1)用向量记号可以写成
若系统(2)存在形式(解析)首次积分,则称它是形式(解析)可积的。设H(x,y)是在原点某邻域中的一个C1函数,显然,H(x,y)是系统(2)的一个C1首次积分当且仅当它在该邻域中满足方程ΔH·FHxP+HyQ≡0;该方程称为系统(1)或系统(2)的可积性方程。
为了介绍拟齐次正规型理论,令m=(t1,t2)是任意给定的非负、无公因子且不全为零的整数对子;设t1≤t2,记|m|=t1+t2表示m的模。设f是一个两变量的标量函数,如果存在整数k,对任意的非负实数ε,满足
则称f是一个m型k次拟齐次函数。显然,若m=(1,1),则f是一个k次齐次函数。
与齐次正规型理论类似,拟齐次正规形理论的关键思想,也是通过选择合适的坐标变换,把系统(3)化为尽可能简单的表达式。对于系统(3),若使用近恒等变换
X=Y+Pk(Y)(4)
其中:Pk∈Qmk,k≥1,则系统(3)变成
其中:I为单位矩阵,Gi(Y)(i=r,r+1,…,r+k,…)称为第i次拟齐次项,容易证明式(5)中,第r次到第r+k-1次拟齐次项都是不变的,即
Gr(Y)=Fr(Y),…,Gr+k-1(Y)=Fr+k-1(Y),
而第r+k次拟齐次项为Gr+k(Y)=Fr+k(Y)-Lr+k(Pk)(Y),其中Lr+k是同调算子:
Lk:Qmk→Qmr+k,
Pk→Lk(Pk)=Pk,Fr=DPk·Fr-DFr·Pk(6)
其中:Pk,Fr=DPk·Fr-DFr·Pk是两个向量场Pk和Fr的李括号,用Range(Lk)表示算子Lk的值域。
显然,式(6)中的算子Lk仅依赖于系统(3)的最低次拟齐次项Fr。为了简化r+k次拟齐次项Fr+k,只需要选择合适的Pk,在Fr+k中消去属于Lk的值域部分。特别地,若Fr+k∈Range(Lk),则可选择合适的Pk,使得Gr+k=0。若Fr+kRange(Lk),由线性代数知识可知,因为Range(Lk)是Qmr+k的一个子空间,所以可选取Range(Lk)在Qmr+k中的一个补空间,记为Cor(Lk),使得
Qmr+k=Range(Lk)Cor(Lk),
于是可以把Fr+k分解成一个直和,消除分解式中属于Range(Lk)的那一部分,就得到了尽可能简单的Gr+k,Gr+k∈Cor(Lk)。
称
为系统(3)的r+k阶截断拟齐次正规型,系统(5)为系统(3)的r+k次拟齐次正规型。
对于平面系统(3),从k=1开始对其作一系列近恒等变换(4),求得r+k次拟齐次正规型(5),然后把变量Y换回到原变量X,就可以得到所要求的拟齐次正规型。但由于Range(Lk)在Qmr+k中的补空间一般是不唯一的,因此所求得的系统(5)也是不唯一的,且有时需要作很多次的近恒等变换(4),最终的近恒等变换是前面所有这样的近恒等变换的复合,所以对于一个具体的微分系统,要求出其拟齐次正规型及相应的近恒等变换十分困难,一般需借助Lie三角形算法[6]实现。另外,由于所作的近恒等变换仅针对系统变量X而没有作时间尺度变换,这样的拟齐次正规型也称为共轭等价正规型。
為了得到系统(3)更为简单的形式,往往先对系统(3)作如下与状态变量有关的时间尺度变换:
其中:λk(X)∈Pmk,k≥1,则系统(3)变为
现在对系统(8)作近恒等变换(4),得到r+k次拟齐次正规型
其中:Hr(Y)=Fr(Y),…,Hr+k-1(Y)=Fr+k-1(Y),而
Hr+k(Y)=Fr+k(Y)-Lr+k(Pk)(Y)-λkFr(Y),
把由此得到的正规型称为系统(3)的拓扑(或轨道)等价拟齐次正规型。
引进同调算子
如同共轭等价正规型情形,这里Hr+k∈Cor(Lk),k≥1。为了简化计算,再引入李导数算子
Range(Lk)=Range(Lk)+Cor(Pk-r)Fr[8],
由文献[8]定理2.2得:当k>t1t2-|m|时,Pmk≠{0},结合引理2知,命题1中的函数H是一个多项式。特别地,如果m=(1,1),对所有的k≥0,Pmk≠{0},于是有下面的推论。
下面介绍文献[8]中有关系统(3)可积性方面的一个重要结论,即命题2。
命题2[8] 设系统(3)中的最低次项Fr(X)为哈密尔顿向量场,并且假设hi+|m|仅有单因式,则系统(3)是形式可积系统当且仅当它的拟齐次正规型是一个零散度系统。
值得注意的是,推论1虽然是针对拟齐次情形,但对于齐次情形也适用,它已经被用来解决一些特殊类型强退化奇点的单值性与可积性等局部定性问题[3,8,11-18]。另外,推论1中的前提条件是最低次项Fr(X)为哈密尔顿向量场且其相应的哈密尔顿函数hi+|m|仅有单因式,否则结果未必成立。近年来,有学者研究,当最低次项Fr(X)为非哈密尔顿向量场或保守部分hi+|m|有重因式时,这种一般系统的单值性或可积性问题[18-22]。
2 主要结论
先给出一个平面微分系统与它的共轭等价系统或轨道等价系统首次积分之间的关系,即定理1和定理2。
定理1 对于平面系统(1),设u=φ(x,y),v=ψ(x,y)是一个可微同胚,系统(1)变为
若F(x,y)是系统(1)的一个首次积分,则F[φ-1(u,v),ψ-1(u,v)]是系统(16)的一个首次积分。
证明 显然系统(16)等号右边的函数为:
U(u,v)=φx[φ-1(u,v),ψ-1(u,v)]P[φ-1(u,v),ψ-1(u,v)]+
φy[φ-1(u,v),ψ-1(u,v)]Q[φ-1(u,v),ψ-1(u,v)],
V(u,v)=ψx[φ-1(u,v),ψ-1(u,v)]P[φ-1(u,v),ψ-1(u,v)]+
ψy[φ-1(u,v),ψ-1(u,v)]Q[φ-1(u,v),ψ-1(u,v)]。
因为F(x,y)是系统(1)的一个首次积分,所以成立恒等式
Fx(x,y)P(x,y)+Fy(x,y)Q(x,y)≡0。
于是
Gu(u,v)U(u,v)+Gv(u,v)V(u,v)=[Fxφ-1u+Fyψ-1u][φxP+φyQ]+[Fxφ-1v+Fyψ-1v][ψxP+ψyQ]=
1J(FxP+FyQ)J=FxP+FyQ≡0,
所以G(u,v):=F[φ-1(u,v),ψ-1(u,v)]是系统(16)的首次积分。
证毕。
若F(x,y)是系统(1)的一个首次积分,则F(x,y)也是系统(17)的一个首次积分。
定理1与定理2表明:平面微分系统(1)与它的共轭等价正规型或轨道等价正规型具有相同的可积性。
Chavarriga等[23]系统地研究了原点是非退化孤立奇点的微分系统
的可积性问题,其中ad-bc≠0;Algaba等[11]研究了一类幂零系统
的可积性,其中m=(1,2n+1);Algaba等[12]研究了形式为
的解析可积性;Algaba等[13]研究了形式为
的解析可积性;Algaba等[3]利用Algaba等[12-13]中的有关结果继续研究了形式为
与
的原点为单值甚至是中心的条件。注意到这些比较具体的系统的最低次项都是守恒的,并且相应的哈密尔顿函数的因式都是单因式,另外,上述文献中的研究与强退化奇点的单值性有关。
考虑下面的平面微分系统
其中:Xk(x,y)与Yk(x,y)是k次齐次多项式,k≥3。显然,原点是系统(18)的强退化奇点。由于这类系统的原点不可能是单值的,因此关于其可积性问题的研究没有引起重视。本文将对最低次是二次齐次的平面微分系统的可积性做比较系统的研究以便获得这类系统的相图。
本文首先给出系统(18)的主系统,即下面的二次齐次多项式微分系统的标准形。
命题3[24] 二次齐次多项式微分系统
经过仿射变换以及时间尺度变换后可得到如下4种标准形:
其中:p1和p2是两个任意常数。
由定理1与定理2可知,本文研究系统(18)的主系统为上述4种标准形之一就可以了。本文仅研究主系统为(19)所对应的系统。
对于微分系统
定理3 系统(24)形式轨道等价于
其中:a(i),b(i),c(i),d(i)∈R,i=0,1,…。
证明 因为F1=F1+t1F1+t2=-2xy-x2+y2,所以由命题1,只需计算Cor(j),j=1,2,3。因为
Pm1=span{x,y};
Pm2=span{x2,xy,y2};
Pm3=span{x3,x2y,xy2,y3};
Pm4=span{x4,x3y,x2y2,xy3,y4}。
如果取μ1∈Pm1,即μ1=α1x+α2y,其中α1,α2∈R,則
如果取μ2∈Pm2,即μ2=α1x2+α2xy+α3y2,其中α1,α2,α3∈R,则
如果取μ3∈Pm3,即μ3=α1x3+α2x2y+α3xy2+α4y3,其中α1,α2,α3,α4∈R,则
于是,由命题1和引理2知,系统(24)的轨道正规型为系统(25)。
证毕。
引理3 对于系统(2),设F∈CωUR2,R2,U是原点的一个邻域。则系统(2)是解析可积的(即Cω-可积的)的充分必要条件是它是形式可积的(即C∞-可积的)。
根据推论1与定理3及引理3,可以得到下面的结果:
定理4 对于系统(24),设右边级数是收敛的,则系统(24)是Cω-可积的充分必要条件是它轨道等价于
3 结 语
本文证明,任意一个平面微分系统,在可微同胚变换以及在原点非零的连续时间尺度变换下,可积性保持不变。特别地,任何一个平面微分系统与它的共轭等价正规型和轨道等价正规型具有相同的可积性。本文引用了最低次是二次齐次系统的标准形(类似于二阶方阵的Jordan标准形)的结果,即命题3,针对其中的一种标准形,在该二次齐次向量场是哈密尔顿的且相应的哈密尔顿函数在复多项式环中的分解式都是单项式的前提下,利用拟齐次正规型理论研究了对应拟齐次系统可积的充要条件。对于最低次是其他3种标准形的系统,可以采用类似的方法进行研究。
由于最低次是二次齐次的平面系统的原点不是单值的,所以很少有学者研究这类系统的可积性问题。但鉴于一个平面系统的首次积分可以决定其相图,进而确定其局部定性结构,在这个意义上,研究最低次是二次齐次的平面系统的可积性,并由此得到所有最低次是二次齐次平面系统的定性分类非常重要。
参考文献:
[1]Arnold V I, IlYashenko Y S. Ordinary differential equations[M]. Berlin: Springer-Verlag, 1988: 54-56.
[2]張芷芬, 丁同仁, 黄文灶, 等. 微分方程定性理论[M]. 北京: 科学出版社, 1985.
[3]Algaba A, García C, Gin J. Analytic integrability of some examples of degenerate planar vector fields[J]. Acta Applicandae Mathematicae, 2016, 141(1): 1-15.
[4]Algaba A, Freire E, Gamero E, et al. Quasi-homogeneous normal forms[J]. Journal of Computational and Applied Mathematics, 2003, 150(1): 193-216.
[5]Algaba A, Freire E, Gamero E, et al. Quasi-homogeneous normal forms for null linear part[J]. Dynamics of Continuous, Discrete and Impulsive Systems Series A: Mathematical Analysis, 2003, 10(1/2/3): 247-261.
[6]Algaba A, Freire E, Gamero E, et al. An algorithm for computing quasi-homogeneous formal normal forms under equivalence[J]. Acta Applicandae Mathematicae, 2004, 80(3): 335-359.
[7]García B, Llibre J, Lombardero A, et al. An algorithm for providing the normal forms of spatial quasi-homogeneous polynomial differential systems[J]. Journal of Symbolic Computation, 2019, 95: 1-25.
[8]Algaba A, Gamero E, García C. The integrability problem for a class of planar systems[J]. Nonlinearity,2009, 22(2): 395-420.
[9]Algaba A, García C, Gin J. Analytic integrability for some degenerate planar vector fields[J]. Journal of Differential Equations, 2014, 257(2): 549-565.
[10]张晶, 黄土森. 一类退化非线性微分方程的正规形计算[J]. 浙江理工大学学报(自然科学版), 2017, 37(6): 866-873.
[11]Algaba A, García C, Reyes M. Characterization of a monodromic singular point of a planar vector field[J]. Nonlinear Analysis: Theory, Methods & Applications, 2011, 74(16): 5402-5414.
[12]Algaba A, García C, Reyes M. Nilpotent systems admitting an algebraic inverse integrating factor over C((x, y))[J]. Qualitative Theory of Dynamical Systems, 2011, 10(2): 303-316.
[13]Algaba A, García C, Reyes M. Existence of an inverse integrating factor, center problem and integrability of a class of nilpotent systems[J]. Chaos, Solitons & Fractals, 2012, 45(6): 869-878.
[14]Algaba A, García C, Gin J, et al. Analytic integrability for some degenerate planar systems[J]. Communications on Pure & Applied Analysis,2013, 12(6): 2797-2809.
[15]Gin J, Llibre J. A method for characterizing nilpotent centers[J]. Journal of Mathematical Analysis and Applications, 2014, 413(1): 537-545.
[16]Valls C, Llibre J. Analytic integrability of a class of planar polynomial differential systems[J]. Discrete and Continuous Dynamical Systems: Series B, 2015, 20(8): 2657-2661.
[17]Algaba A, Gamero E, García C. The center problem. A view from the normal form theory[J]. Journal of Mathematical Analysis and Applications, 2016, 434(1): 680-697.
[18]Algaba A, Checa I, García C, et al. Analytic integrability inside a family of degenerate centers[J]. Nonlinear Analysis: Real World Applications, 2016, 31: 288-307.
[19]Algaba A, García C, Reyes M. Invariant curves and analytic integrability of a planar vector field[J]. Journal of Differential Equations, 2019, 266(2/3):1357-1376.
[20]Algaba A, García C, Gin J. Analytic integrability around a nilpotent singularity[J]. Journal of Differential Equations, 2019, 267(1): 443-467.
[21]Algaba A, García C, Reyes M. Algebraic integrability of nilpotent planar vector fields[J]. Chaos, Solitons & Fractals, 2021, 145: 110765.
[22]Jaume L, Yuzhou T. Generalized Analytic Integrability of a Class of Polynomial Difffferential Systems in C2. [J]. Acta Applicandae Mathematicae, 2021, 173: 1-17.
[23]Chavarriga J, Giacomini H, Gin J, et al. On the integrability of two-dimensional flows[J]. Journal of Differential Equations, 1999, 157(1): 163-182.
[24]García B, Llibre J, Prez del Río J S. Planar quasi-homogeneous polynomial differential systems and their integrability[J]. Journal of Differential Equations, 2013, 255(10): 3185-3204.

