基于Matlab的女裤参数化制版方法
段欣瑜 吴巧英
摘 要: 为进一步提高服装CAD 制版效率,满足个性化服装制版的快速响应要求,以女裤为研究对象,基于Matlab软件开发平台,设置关键参数和调节参数2种参数变量,通过参数驱动数学模型数据计算及纸样绘制程序,生成多款式且结构合理的女裤纸样,并将贝塞尔曲线拟合方法应用于参数化制版中,最后对提出的参数化制版方法进行验证。结果表明:运行参数化制版程序,可实现女裤纸样的款式变化、参数调节功能;从约束条件出发对裤装曲线进行拟合,裤装曲线能自动更新,满足新生成女裤结构合理性的要求。经参数化制版验证,本文提出的参数化制版方法可以满足女裤个性化自动化的服装制版要求。
关键词: Matlab;贝塞尔曲线;参数化制版;女裤纸样
中图分类号: TS941.2
文献标志码: A
文章编号: 1673-3851 (2024) 03-0220-09
Parameterized plate making method for women′s pants based on Matlab
Abstract: To further improve the efficiency of clothing CAD plate making and meet the fast response requirements of personalized clothing plate making, women′s pants were taken as the research object. Based on the Matlab software development platform, two parameter variables, key parameters and adjustment parameters, were set. Through parameter-driven mathematical model data calculation and paper sample drawing program, multiple styles and structurally reasonable women′s pants paper samples were generated. The Bessel curve fitting method was applied to parameterized plate making. Finally, the proposed parameterized plate making method was verified. The results show that running a parameterized plate making program can achieve the functions of changing the style and adjusting parameters of women′s pants patterns. Fit based on constraint conditions, the pants curve could be automatically updated to meet the rationality requirements of the newly generated women′s pants structure. It is verified through parameterized plate making that the parameterized plate making method proposed in this article can meet the requirements of personalized and automated clothing plate making for women′s pants.
Key words: Matlab; Bezier curves; parameterized plate making; women′s pants pattern
0 引 言
在供給侧结构性改革背景下,服装产业定制化转型已成为行业共识。传统的服装大规模生产模式难以满足消费者时尚化、多样化以及个性化的需求,大规模定制和个性化定制已经被视为最有前景的服装生产方式之一[1-2]。服装CAD制版是计算机辅助设计在服装生产技术应用中最重要的技术之一,如美国格柏系统、法国力克系统及国内的富怡、日升等服装CAD技术的广泛使用,提高了制版效率,但在实际生产中尚未能满足服装个性化定制的快速制版需求[3]。目前流行的三维服装建模技术极大地推动了数字化发展进程,但二维纸样的反复修正造成了设计流程与周期延长的问题[4],因此迫切需要研发能在三维服装建模技术应用前端进行衔接的纸样自动生成技术,缩短服装的开发周期。目前对服装纸样自动生成技术的研究主要集中在二维平面纸样参数化及三维服装模型展平两方面[5]。从实际应用角度考虑,衔接数字化进程、满足个性化服装制版快速响应要求的最有效方法就是开发参数化服装制版的 CAD 技术[6]。服装纸样参数化的研究从早期利用服装专用 CAD 制图软件实现服装纸样的自动设计[7-9],到使用其他通用的数字图像处理软件如Matlab、AutoCAD进行参数化绘图等,其研究的重点在于提高自动生成纸样的质量与生成效率[10-11]。上述研究为本文参数化制版方法提供了有益参考,然而仍有一些困难需要克服:a)现有研究侧重于服装规格和局部造型的变化,尚缺乏兼顾款式变化及结构合理性要求的参数化设计研究;b)曲线拟合方法在服装参数化制版中应用的准确性难以保证;c)缺乏试衣验证实验,仅进行参数化制版的应用测试,忽略了生成纸样结构合理性的验证。
与AutoCAD相比,Matlab开发难度相对较小、成本较低,且具有强大的图像处理功能、便捷实现参数化输入与可视化图形输出的功能[12]。因此,本文以女裤为研究对象,基于Matlab研究服装参数化制版,以期实现较为完善的个性化自动化服装制版流程。针对上文提到的目前研究中遇到的一些困难,本文将从以下几个角度探究解决方法:增加参数设置,以常规的服装规格、款式变化相关的参数设置为基础,增加局部的调节参数设置,使生成的女裤纸样能同时兼顾款式变化及结构合理性的要求;从曲线约束的角度出发绘制女裤结构曲线,确保参数化制版生成曲线的准确性;补充试衣测试与应用测试,验证提出的参数化制版方法的可行性。
1 参数化制图原理
参数化制图是一种基于所输入的参数来约束和描述几何图形结构尺寸的作图方法,该方法可以根据所输入的不同参数序列值驱动程序中的算式约束快速获得新的目标几何图形[13]。本文将参数化制图的方法应用在女裤纸样设计中,通过设置参数变量等一系列制版流程,来实现女裤纸样自动生成的目的并进行验证。
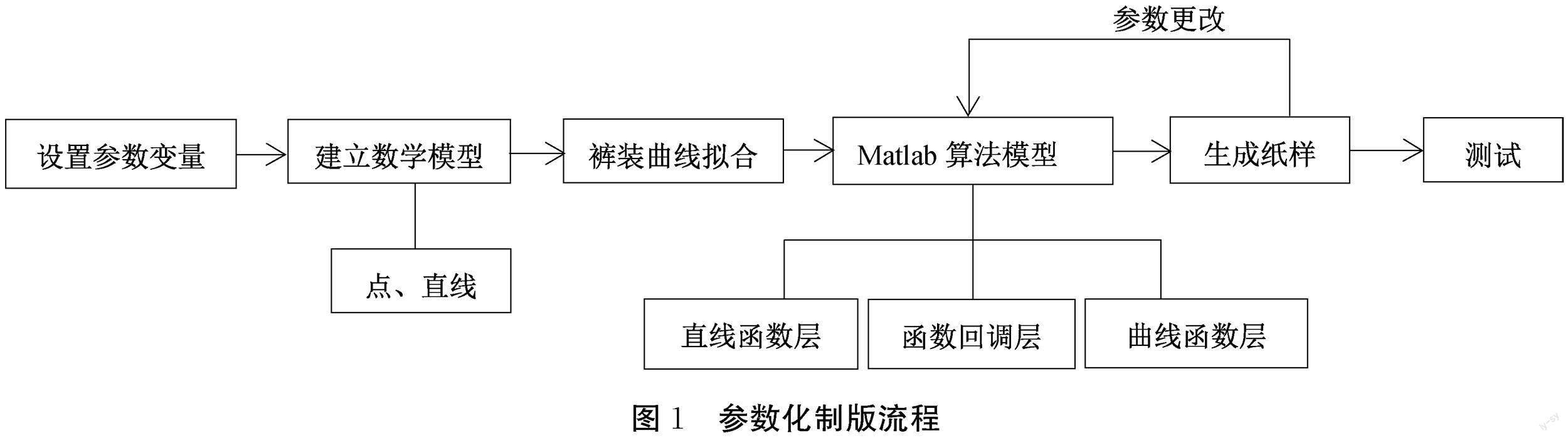
1.1 参数化制版流程
本文设计的参数化制版流程如图1所示。首先,根据女裤制版所需的结构参数设置参数变量,建立参数化制版的数学模型,即可确定点的坐标与直线轮廓。其次,研究裤装曲线拟合方法,并结合Matlab软件对直曲线的绘制过程进行算法描述,即可构建女裤参数化的算法模型,该模型包含直线函数层、曲线函数层、函数回调层,用于生成完整纸样,且当纸样参数需要更改时,女裤参数算法模型可以驱动程序重新生成新的纸样。最后,对生成纸样进行实际着装与虚拟试衣测试,以验证该参数化制版方法是否可行。
1.2 结构参数分析
本文将女裤制版所需结构参数分为两类。一类是关键参数,依据人体尺寸及女裤造型设计需要设置,主要包括人体腰围w0、上裆长d0、膝长e0、裤臀围h、裤膝围k、裤口围b、裤长c、裤腰线下落量w1和裤膝线提升量k1,基于以上关键参数,可以获得女裤的基础纸样;另一类是调节参数,主要依据服装内部的结构关系,该参数取值大小受女裤宽松度的影响,包括前后片落裆量调节值(a1、a4)、横裆宽调节值(a2、a5)、后中斜率调节值(a3)及后挺缝线偏移量(a6),通过以上调节参数的更改,可以进一步提高女裤结构的合理性。
2 基于Matlab制版
2.1 计算数学模型
女裤制图方法参考《女装结构设计与产品开发》[14],以160/68A中间体为例,绘制女裤纸样。以女裤前片纸样为例,将臀围线与裤中线交点(P0)设为原点,建立直角坐标系,根据各部位结构尺寸的计算公式计算得到各关键点坐标,将样版设计中尺寸与结构的关系转化成了平面直角坐标系内点与线的关系,从而确定了女裤的数学模型。女裤前片结构设计关键点标注如图2所示,各部位结构尺寸的表达式及标注如表1所示。
女裤前片的落裆量与横裆宽尺寸主要受女裤臀围松量的影响[15],运动机能良好的条件下臀围松量变化范围为0~12.0cm[16]。按照臀围松量大小将女裤分为合体型(0~4.0 cm)、基本型(4.0~8.0 cm)和宽松型(8.0~12.0 cm),并设置前片落裆量调节值a1、前片横裆宽调节值a2,对应3种类型女裤的初始值分别为:a1为0、0.5 cm和1.0 cm;a2为-0.7、-0.4 cm和0 。考虑到女裤结构的复杂性,针对特殊体型的服装纸样,裆部的调节参数还可以自行输入进行调节。综上,根据表1女裤前片各部位结构尺寸的计算公式,可以推得图2中各关键点坐标,结果见表2。
2.2 裤装曲线拟合
女裤前片的曲线分别有腰线、裤侧缝线、上裆缝线和裆弯线,这些曲线可以根据其约束特点分为切线约束曲线和必经點约束曲线2类,本文采用贝塞尔曲线拟合方法对这2种情况的曲线进行精确绘制。
2.2.1 切线约束曲线
贝塞尔曲线是参数曲线的一种,因其具有良好的造型拟合能力,在服装 CAD 制图软件和计算机图形处理软件中应用广泛。服装中部分曲线要求其在端点处切线斜率一定,而贝塞尔曲线具有始末端点与对应特征多边形的首尾两条线段相切的性质[17],因此通过调节邻端点处控制点的位置(如B1、B2)可以满足服装曲线在端点处切线斜率一定的要求(见图3)。
在女裤前片纸样中,局部腰线S0P4与侧缝线上段P4P6夹角为90°,且其在S0、P6点处分别相切于水平、竖直线,如图4(a)所示;侧缝线下段P6P10在两端点处分别相切于两条竖直线,如图4 (b)所示。由于这些曲线都符合在端点处受切线约束的特点,分别以S0、A1、P4和P4、A2、P6为控制点绘制两条二次贝塞尔曲线,即完成腰围曲线与侧缝线上段曲线的绘制;在P6、P10所在竖直线上找到中间控制点P6、P10绘制一条三次贝塞尔曲线,即完成侧缝线下段曲线的绘制,其中P6P6与P10P10的长度经调试取8.0 cm时曲线效果较优。同理,以P7、P9、P9为控制点绘制下裆缝线P7P9。
2.2.2 必经点约束曲线
服装中一些曲线除了要保证线条平滑圆顺、切矢量方向一定、还要满足过关键点的要求,如前裆弯曲线(见图5),该曲线过必经点Pb,且在P5点处与P3P5的延长线切线1相切,在P7点处与切线2相切(切线2与P7P9的垂线的夹角为ɑ,该角度与后片下裆缝线与竖直线夹角相同)。根据贝塞尔曲线特性,设置两个邻端点处控制点分别位于切线1和切线2上,则以此绘制三次贝塞尔曲线可满足切线斜率要求,此外,要使曲线经过Pb点,还需要添加其他约束条件。顾一帆等[18]通过解方程组法计算控制点坐标来解决贝塞尔曲线过必经点的问题,计算较复杂且没有考虑到服装曲线端点相切的特点。本文从曲线特点出发对服装曲线进行分类,从几何角度探究服装曲线拟合的一般方法:过n个点绘制圆顺曲线,则依次过必经点绘制切线,分别以相邻两必经点及其切线交点为控制点绘制二次贝塞尔曲线,则以n-1段二次贝塞尔曲线拟合而成的曲线满足曲线圆顺、过必经点要求。
以裆弯弧线绘制为例:n=3,已知该曲线在两端点处的切线,过Pb点再画一条切线,分别与切线1、切线2交于B、C两点,B、C两点可沿P5Pd、P7Pd滑动,其斜率介于切线1、切线2之间(见图6),具体值由制图者凭经验决定。经试验可得BC斜率取值近似1时曲线形态较好,故将BC斜率取为1,再分别以P5、B、Pb和Pb、C、P7为控制点绘制两段贝塞尔曲线,则所绘制裆弯弧线满足要求。
2.3 Matlab实现
2.3.1 程序编写
Matlab是一款具有强大计算能力的数学软件,能便捷地实现参数化输入和可视化的图形输出[19],本文基于2.1节建立的结构数学模型及2.2节总结的女裤制版方法,将其转化成程序语言,利用 Matlab的R2018b 版本中plot函数进行坐标点的连接,对于曲线部分的绘制,则需要对曲线的表达式进行求解,保存散点并依次连接曲线点。
如三次贝塞尔曲线拟合裤侧缝线下段P6P10,主要代码如下:
for t=0:0.01:1;
P_t_1=(1-t) * P6+ t * P6;
P_t_2=(1-t) * P6+ t *P14;
P_t_3=(1-t) * P14+ t *P14;
P_t_4=(1-t) * P_t_1 + t * P_t_2;
P_t_5=(1-t) * P_t_2 + t * P_t_3;
P_t_6=(1-t) * P_t_4 + t * P_t_5;
PP=[PP;P_t_6];
plot(PP(:,1),PP(:,2),′-r′);
end
又如分段贝塞尔曲线拟合裆弯弧线P5P7,联立线性关系式求解中间控制点B、C的坐标,其中k35、k7d、kBC分别为切线1、切线2、BC三条切线的斜率,其主要代码如下:
syms x y;
[x,y]=solve(kBC*x+pb(2)-kBC*pb(1)-
y==0,k35*x-p5(1)*k35+p5(2)-y==0 );
B=[x,y];
syms x y;
[x,y]=solve(kBC*x+pb(2)-kBC*pb(1)-
y==0, k7d*x-p7(1)*k7d+p7(2)-y==0);
C=[x,y];
逐步完善绘图代码,将该程序命名为 Pants Sample。运行程序时,计算机根据输入参数计算点坐标,并在坐标系中绘制出女裤纸样轮廓。
2.3.2 纸样自动生成
在Matlab的命令窗口中输入guide命令并运行,设置女裤自动生成的用户界面,如图7所示。该界面有两个窗口,在“参数设计”窗口输入绘制女裤所需的关键尺寸,点击“图形预览”即可自动生成对应的女裤纸样,在“参数调节”窗口还可以修改调节参数的数值对已生成纸样进行局部调节。接下来,以臀围94.0 cm(放松量4.0 cm)直筒裤为例,输入w0=“68.0”、d0=“25.5”、e0=“54.0”、h=“94.0”、k=“44.0”、b=“40.0”、c=“96.5”、w1=“0”、k1=“0”,其余参数为默认值,点击“图形预览”,生成女裤前后片纸样效果见图7。此外,为使生成女裤纸样对接实际生产及在虚拟试衣系统中应用,在用户界面设置格式转化功能,可将Matlab绘制女裤纸样自动保存为DXF格式。
3 参数化制版方法验证
3.1 参数化制版试衣测试
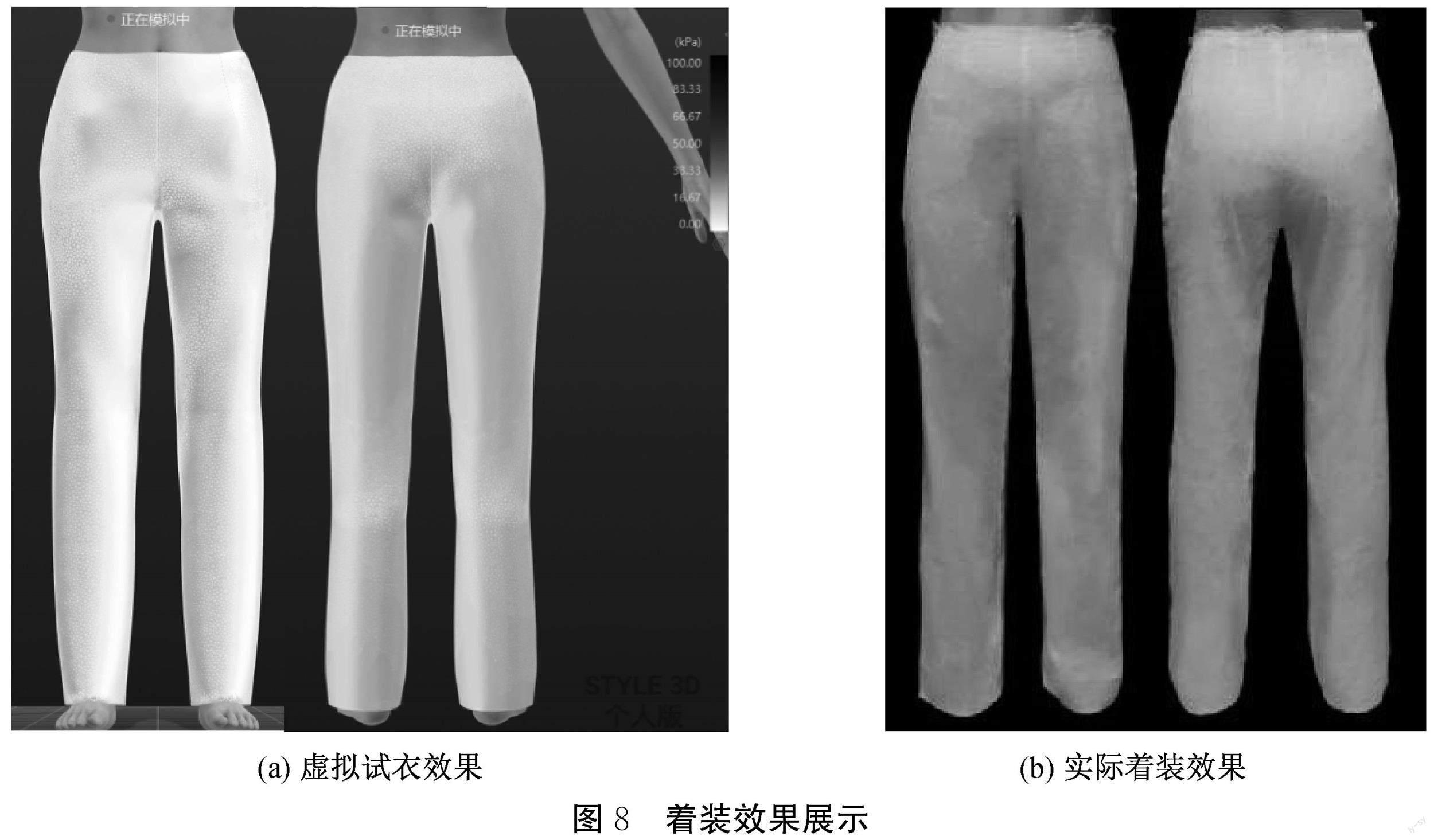
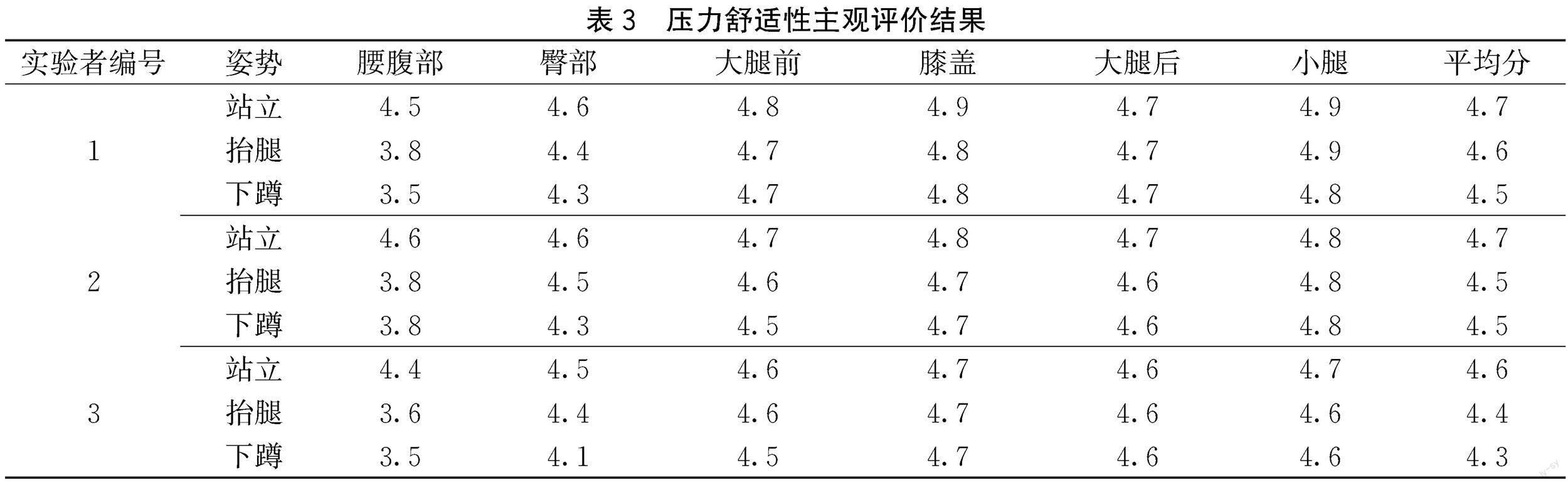
将2.3.2中自动生成DXF格式的女裤纸样导入Style3D虚拟试衣软件中,按照160/68A中间体女性的人体尺寸设置模特的身高、腰围和臀围等尺寸,利用虚拟缝合工具对女裤进行基础人体模型的虚拟试穿,观察其在虚拟试衣系统中正面、背面的着装效果(见图8(a)),虚拟试衣压力图整体呈现浅色,表明该女裤在Style3D拟试衣状态下的着装舒适性较高[20]。实际着装效果验证,输出1∶1纸样制作该实验女裤的白坯样衣,再将白坯样衣实际穿着在160/68A的人体模特上,着装效果如图8(b)所示。根据着装效果可见,实际着装与虚拟试衣状态下,该纸样的穿着状态均良好。再选取3位接近中间体尺寸特征的女性进行着装压力舒适性主观评价,评价分为5个级别(1为非常不舒适;2为不舒适;3为一般;4为舒适;5为非常舒适),受试者分别取站立、抬腿和下蹲3种姿势,对穿着实验女裤时腰腹部、臀部、大腿前、膝盖、大腿后和小腿6个部位进行压力舒适性评价。从评价结果表3可见,三种姿势下各部位舒适性评价平均分在4.3~4.7分,其中抬腿、下蹲姿势时,腰腹部松量主要依赖人体腰围的可塑性,舒适性评价分值相较于站立姿势略低,但整体介于3.5~3.8分,整体着装舒适性较好。因此认为该实验女裤参数设置合理且具备较好的合体性与美观性。
再选用3款不同造型的经典女裤纸样,关键参数设置如表4所示,调节参数设为默认值,虚拟试衣压力示意图如图9所示,3款女裤纸样着装后压力图整体呈现浅色,均处于低压力值区间。
综上,本文提出的参数化制版方法生成女裤纸样的结构合理性较高。
3.2 参数化制版应用测试
对基于Matlab的参数化制版在应用中的纸样款式变换、参数调节功能及曲线拟合方法的合理性进行测试。
测试一。以国标160/68A女性的臀围94.0 cm(放松量4.0 cm)女直筒裤为基础纸样(图10中实线),保持腰围尺寸及与人体规格尺寸相关的上裆长、膝长的数值不变,在其余6个关键参数中每次取其中一个参数进行调整,从而快速生成不同款式变化的女裤纸样。用于款式变化的参数化调整纸样对比图如图10所示,参数化调整数据如表5所示。从纸样生成效果来看,女裤纸样的臀围、膝圍、脚口围、裤长、腰围线位置、膝围线位置均可以根据不同的参数设置进行调整。
测试二。只调整女裤的臀围松量,调节参数默认取值自动调整优化纸样结构,从而快速生成不同臀围放松量的女裤纸样。以放松量以2.0、6.0 cm和10.0 cm为例,臀围松量变化的参数化调整对比图如图11所示。由图12可见,随着臀围松量增大,女裤前后片的横裆宽、横裆深都逐渐增大,后中心线L的斜率绝对值逐渐增大,后挺缝线向后移动,达到纸样设计要求。
测试三。检测裤装曲线拟合方法合理性。以裆弯曲线为例,其他参数不变,只改变臀围松量或膝围尺寸,快速生成女裤纸样,参数化调整后裆弯曲线对比图如图12所示。图12表明:臀围松量增大时,裆部曲线起伏量逐渐增大且始终相接圆顺,膝围k减小,前片裆部曲线起伏量随之增大以保证前后片始终互补,因此本文的曲线拟合方法能实现曲线的自动更新以满足新的纸样要求。
综上,参数设计与参数调节相结合并细化曲线拟合方法,绘制出的女裤纸样既能满足造型变化功能又能满足纸样结构合理性要求。
4 结 论
本文结合Matlab设置参数,建立参数化制版的数学模型,确定点的坐标与直线轮廓,并将贝塞尔曲线拟合方法应用于服装参数化制版的曲线轮廓绘制,最终通过GUI界面将自动生成纸样进行格式转化,与虚拟试衣软件对接。经参数化制版的试衣测试与应用测试发现,本文提出的参数化制版方法自动生成的女裤纸样具有以下特点:
a)任意参数均可调整。除了与人体规格、造型设计相关的关键参数外,本文还设置了调节参数,可以对局部如前中线斜率、横裆宽及落裆量进行调节,因此自动生成的纸样造型多样且服装结构得到了进一步优化。
b)从约束条件考虑设置曲线拟合方法,能实现曲线的自动更新且精准度较高,如裆弯曲线既能保持前后片裆部的圆顺效果,又能保证大小裆的夹角始终互补。
c)按照本文提出的参数化制版方法可快速生成不同造型的女裤纸样,经虚拟试衣压力测试其舒适性良好,提高了制版效率,可用于裤装个性化制版。
参考文献:
[1]王璐璐, 王军, 伞文,等. 数字化服装设计的发展与技术创新研究[J]. 山东纺织科技, 2016, 57(5):35-38.
[2]Jin P, Fan J T, Zheng R, et al. Design and research of automatic garment-pattern-generation system based on parameterized design[J]. Sustainability, 2023, 15(2): 1268.
[3]竺梅芳. 智能化服装CAD制版技术发展研究[J]. 浙江纺织服装职业技术学院学报, 2016, 15(2):38-40.
[4]宋莹, 相思曼, 孙雅致. 基于虚拟仿真技术的服装逆向流程优化设计[J]. 丝绸, 2022, 59(4):59-64.
[5]雷鸽, 李小辉. 数字化服装结构设计技术的研究进展[J]. 纺织学报, 2022, 43(4):203-209.
[6]Liu K X, Zhu C, Tao X Y, et al. Parametric design of garment pattern based on body dimensions[J]. International Journal of Industrial Ergonomics, 2019, 72:212-221.
[7]王燕珍. 男衬衫样板参数化智能生成研究[J]. 上海纺织科技, 2008, 36(7):8-11.
[8]叶勤文, 张皋鹏. 基于AutoCAD参数化的个性化服装纸样生成[J]. 纺织学报, 2019, 40(4):103-110.
[9]陈咪, 叶勤文, 张皋鹏. 斜裁裙参数化结构模型的构建[J]. 纺织学报, 2020, 41(7):135-140.
[10]王成佐, 朱江龙, 余俊雅,等. 基于AutoLISP的男西服样板自动化生成[J]. 毛纺科技, 2022, 50(3):98-105.
[11]张伶俐, 张皋鹏. 应用Matlab的服装纸样参数化平面制版[J]. 纺织学报, 2019, 40(1):130-135.
[12]凌雅丽, 朱凌轩, 邵晓煊, 等. 亚洲男士西服基本纸样自动生成系统的建立[J]. 纺织学报, 2020, 41(9):108-113.
[13]王宗荣, 张皋鹏. 新版文化女装衣身原型参数化制图数学模型[J]. 纺织学报, 2009, 30(3): 82-87.
[14]朱秀丽, 吴巧英. 女装结构设计与产品开发[M]. 北京:中国纺织出版社, 2011:282-328.
[15]謝勇, 吴秋英, 肖劲蓉, 等. 臀围松量对女裤裆部特征的影响分析与模型构建[J]. 丝绸, 2020, 57(11):41-45.
[16]刘东. 影响短裤裆位的因素及结构分析[J]. 东华大学学报(社会科学版), 2010, 10(1):74-76.
[17]代文猛, 年春波, 杨洋,等. N次Bezier曲线的多边形快速逼近算法[J]. 机械科学与技术, 2018, 37(12):1902-1907.
[18]顾一帆, 史有群. 服装CAD制版系统中曲线绘制自动化方法研究[J]. 计算机科学与应用, 2019, 9(1):9-18.
[19]史洁玉, 孔令军. MATLAB R2012a超级学习手册[M]. 北京:人民邮电出版社, 2013:72-138.
[20]朱蕾. 基于Style3D技术的女装翻驳领结构优化[J]. 毛纺科技, 2023, 51(1):70-75.

