基于新型滑模观测器的PMSM无传感器控制
罗晓东,周士贵,曹凤斌,柴方博,张可程
(1.曲阜师范大学 工学院,日照 276800; 2.日照东方电机有限公司,日照 276800)
0 引 言
永磁同步电机因具有效率高、功率密度高、可靠性高等特点而应用广泛,但其存在的机械传感器在提高可靠性的同时也加大了控制系统的成本,增大了系统的体积,使永磁同步电机在某些特定场合下应用困难,所以研究永磁同步电机无传感器控制是实用并且有价值的。在无传感器控制的众多方法中,滑模观测器法因其鲁棒性强和对电机参数不敏感等优点而被广泛观注,成为众多专家学者们争先恐后研究的对象。
文献[1]提出用定结构滑模控制器与扩展滑模扰动观测器相结合的方法,文献[2]提出的滑模增益自适应滑模观测器,两者都削弱了抖振,提高了转子位置的观测精度,但参数整定比较复杂。另外,文献[3-4]都在滑模观测器的切换函数上进行了改进,在一定程度上削弱了系统的高频抖振,但其收敛性能降低。文献[5]提出利用高阶滑模例如非奇异终端滑模面来削弱转速抖振、提高响应速度和稳态性能,但参数整定较为复杂。文献[6-7]将神经网络、模糊控制等智能控制算法和电机控制的经典算法相结合,来增强系统的鲁棒性和稳定性,缺点是其参数整定复杂,调试困难。
为了解决上述问题,本文提出了一种改进型的滑模观测器。首先,设计了一种新的趋近律,并将滑模增益Ksw和模糊控制相结合;其次,将传统的符号函数用饱和函数来代替,实现稳定平滑切换,并将传统的PI控制器用二阶滑模控制器来替代,实现平稳控制;最后,通过仿真验证了本文方案在稳态性能和抗干扰性能上都优于传统的滑模观测器。
1 扩展滑模观测器设计
1.1 表贴式永磁同步电机的数学模型
表贴式永磁同步电机在α、β坐标系下的数学模型:
(1)
式中:iα、iβ,uα、uβ,Rs分别代表α、β坐标系下的定子电流、定子电压以及定子电阻;Ls为相电感;ωe为实际电角速度;vα=-ωeψfsinθe,vβ=ωeψfcosθe;θe为转子电角度。
1.2 传统滑模观测器设计
构造滑模观测器如下:
(2)
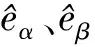
设计扩展反电动势的滑模控制律:
(3)
式中:k值需要满足滑模的存在性、稳定性等条件。到达滑模面之后会一直保持在滑模面上,到达滑模面时s(x)=0,此时的控制量可以看作是等效控制量。可以得到:
(4)

1.3 新型滑模观测器控制律设计
结合指数和幂次趋近律,初步趋近律设计:
(5)
式中:K表示滑模系数;s表示设计的滑模面;a是一个正常数且小于1;ε大于零。如果系统在滑模面附近,sign函数输出值只有-1和1两个值,切换不连续,会加剧控制量的不连续性,所以采用饱和函数sat代替sign函数,实现滑模状态平滑切换,以此来降低系统的抖振。
改进后的趋近律设计:
(6)
1.4 模糊滑模增益设计
模糊控制系统的输入变量为系统观测电流误差和观测电流误差的变化率,输出变量为滑模增益Ksw。输入变量的模糊语言为{NB(负大)、NM(负中)、NS(负小)、PS(正小)、PM(正中)、PB(正大)},输出变量的模糊语言为{PS(正小)、PM(正中)、PB(正大)},输入变量和输出变量的论域均为{-1,1},输出滑模增益Ksw的模糊控制规则设计如表1所示。
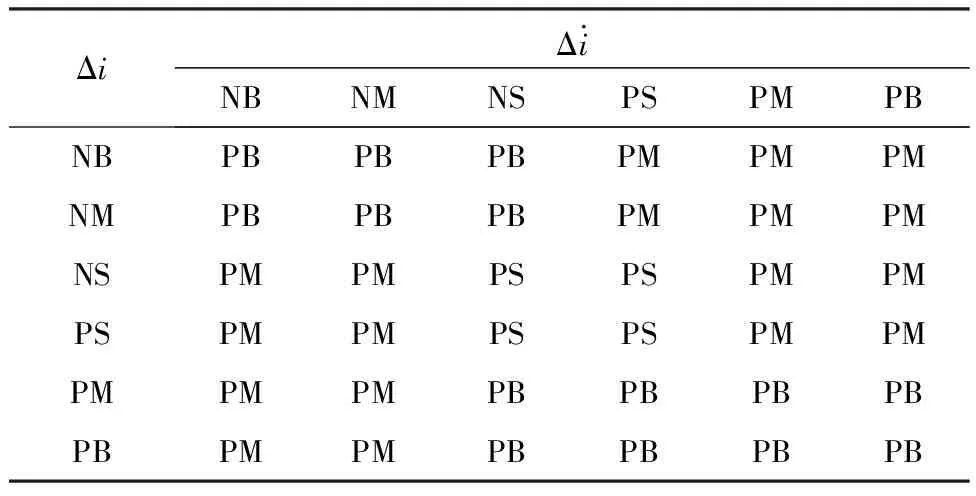
表1 模糊控制规则表
根据表1的模糊控制规则,可实现滑模增益Ksw的动态调整,起到削弱抖振的作用。用模糊自适应ρ(t)代替传统固定增益,新滑模趋近律如下:
(7)
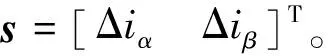
改进后的滑模控制律如下式:
(8)
可以看出,系统的稳定性由ρ(t)、ε决定,所以构造Lyapunov函数:
V=sTs/2
(9)
稳定性条件:
(10)
对V求导得:
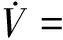
(11)
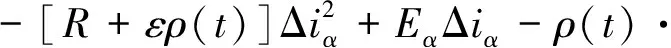
ρ(t)≥(Eα-RΔiα)/{[Δiαsat(Δiα)]a+εΔiα}
(12)
当Δiα<0时,满足式(13)才能实现式(12)。Y1的分析方法类似。
[Δiαsat(Δiα)]a+εΔiα<0
(13)
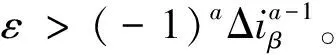
ρ(t)≥max{(Eα-RΔiα)/{[Δiαsat(Δiα)]a+εΔiα},
(Eβ-RΔiβ)/{[Δiβsat(Δiβ)]a+εΔiβ}}
2 二阶滑模控制器设计
2.1 二阶滑模控制器原理
为改善控制系统中d轴和q轴输出电压波形,降低系统的抖振,将传统PI控制器用二阶滑模控制器(S_T SMC)代替。下面介绍二阶滑模控制器设计原理。
首先定义一个非线性控制系统:
(14)
式中:x表示系统的状态变量;y表示控制系统的输出;u表示控制变量;a(t,x),b(t,x)都是连续的未知函数。系统收敛的条件是滑模面函数c(t,x)能够在有限的时间内趋于0。对滑模面函数进行二次求导得:
(15)
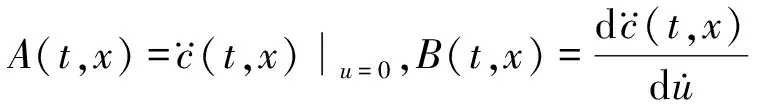
(16)
若满足式(16)条件,可得:
(17)
若系统能在很短的一段时间内满足c(t,x)的一阶和二阶导数都等于0,并且滑模面满足式(17)的形式,那么二阶滑模控制算法控制函数u可以定义如下:
(18)
式中:Kp,Ki都为正数且满足式(19)的约束条件:
(19)
若式(15)满足式(16),且式(18)满足式(19),那么认为二阶滑模控制系统能够在较短的时间内收敛。
综上所述,q轴二阶滑模控制器设计框图如图1所示,d轴同理。
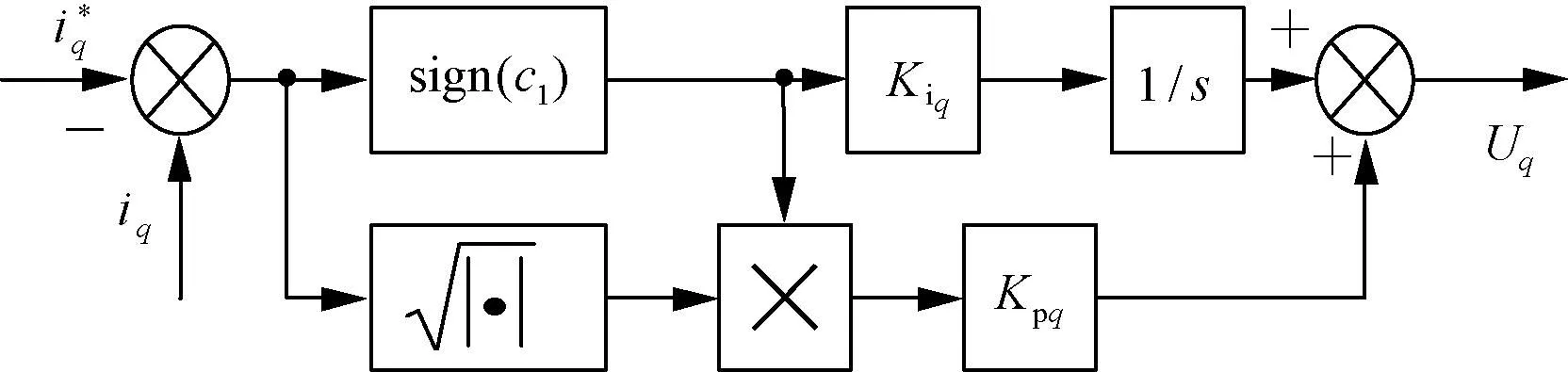
图1 q轴二阶滑模控制器设计框图
2.2 二阶滑模控制器参数设计
d、q坐标系下PMSM定子电压方程:
(20)
将式(20)改写为式(21):
(21)
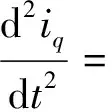
(22)
同理得:

(23)
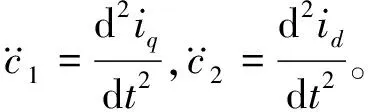
式(22)和式(23)中,Ld、Lq、R、ψf都是常数,Ud、Uq和ωe都是有界函数,式(22)和式(23)满足式(16)的条件。
q轴的二阶滑模控制器可以设计为下式:
(23)
式中:Kpq,Kiq两个参数要满足式(19)。d轴同理。
(24)
(25)
可得q轴和d轴二阶滑模控制器结构如图2所示。
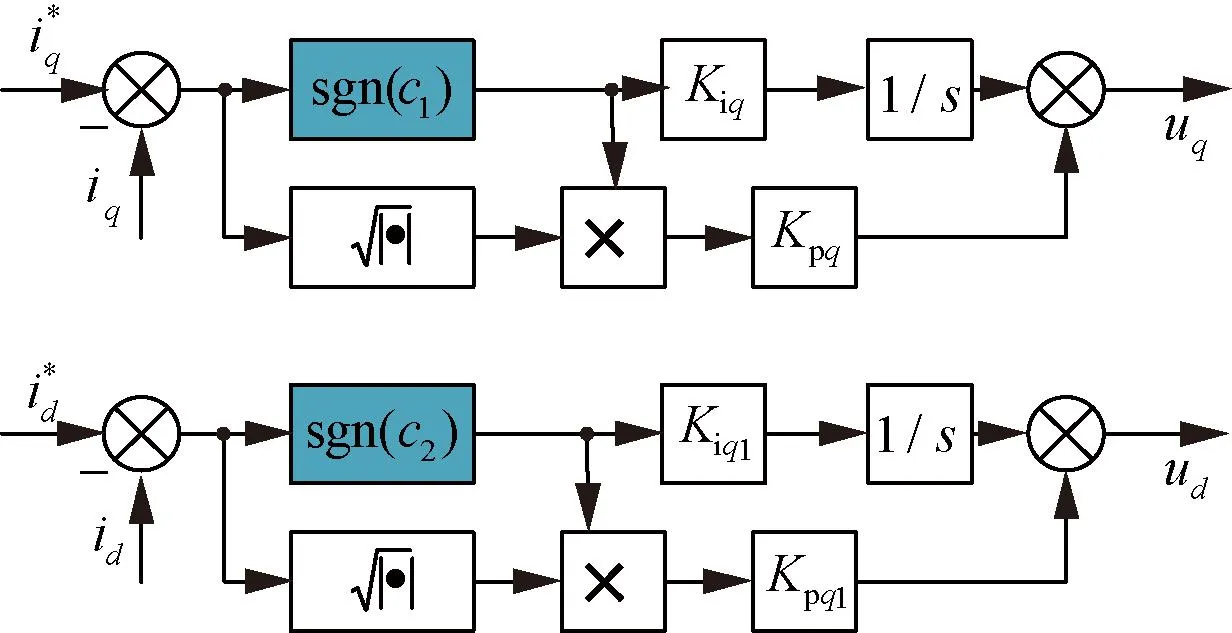
图2 优化后的q轴和d轴二阶滑模控制器设计框图
3 仿真验证
为验证本文方案的有效性,在MATLAB环境下对本系统进行仿真验证。其中逆变器的直流母线电压UDC为311 V,极对数为4,定子电感Ls=8.5×10-3mH,定子电阻Rs=3.875 Ω,永磁体磁通ψf=0.175 Wb,转动惯量J=0.001 kg·m2。控制过程的参数设置:转速环PI设置Kp=0.05,Ki=20,二阶滑模控制器参数设置Kiq=125,Kpq=500,滑模增益利用模糊控制,模糊规则在前文已经介绍。传统的SMO控制转速环PI设置Kp=2,Ki=1.5,电流环参数设置Ki=100,Kp=100,切换函数使用传统的符号函数,滑模增益Ksw=100。将本文算法与传统SMO-PLL进行仿真对比,图3为转速给定500 r/min时,本文方法和传统SMO的转速和转子位置对比。可以看出,无论是起动阶段还是稳定后,新型滑模相比传统滑模抖振更小,稳定后转速波动仅为±3 r/min,并且角度跟踪效果也更好,适用于动态误差要求不高、静态误差要求高的场合。图4表明,在突加一个大小为2 N·m的负载后,本文方案转速下降30 r/min,传统SMO转速下降了40 r/min,本文方案比传统方案转速跌落要少10 r/min左右。图4还比较了突加负载时的三相电流波形和转矩波形。可以看出,新型滑模无论是空载还是带载抖振都比传统滑模要小得多,再次证明了本文方案的控制效果比传统方案更好。
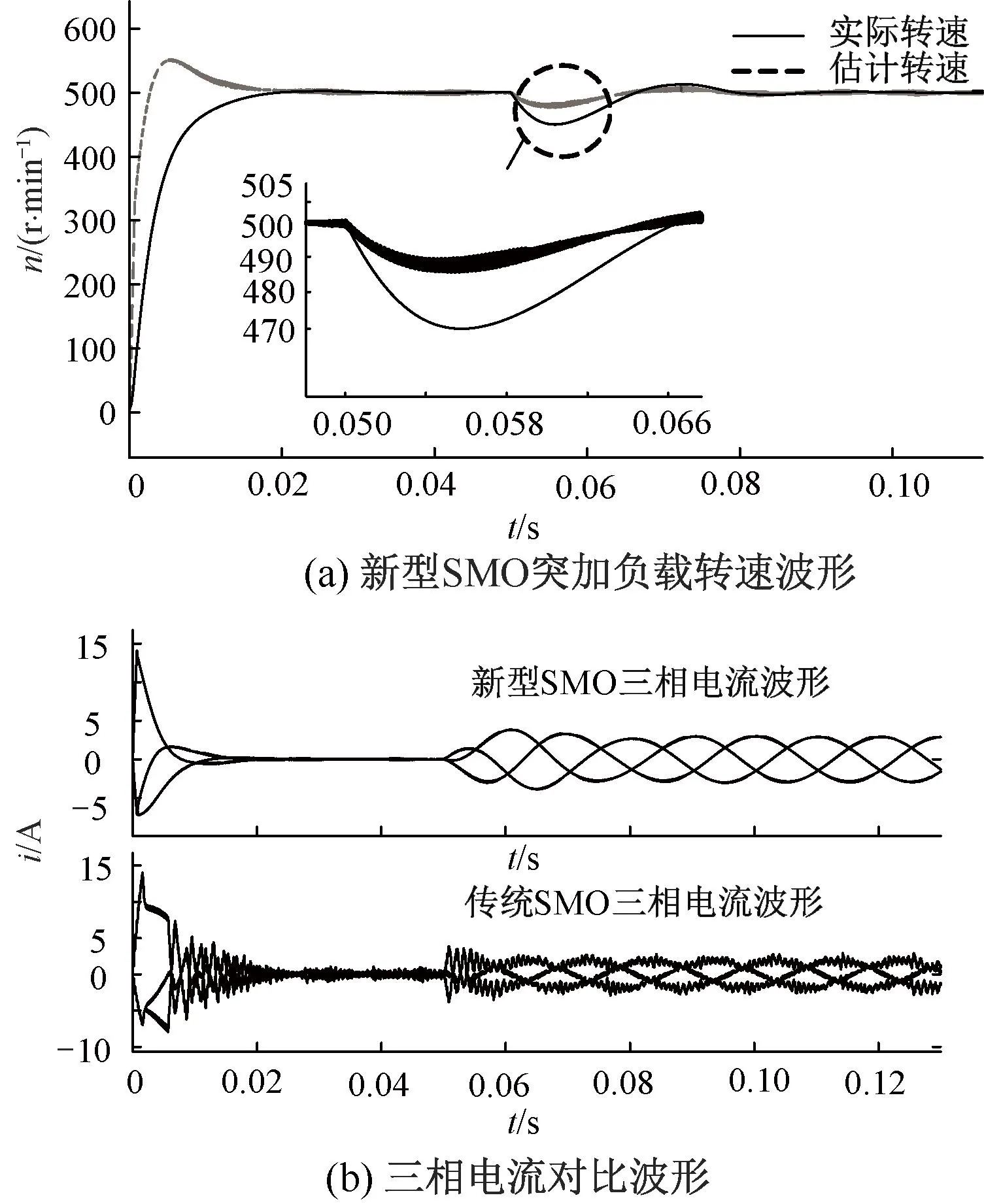
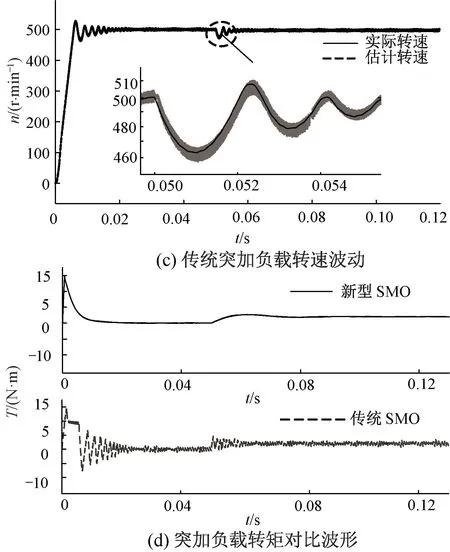
图4 突加负载时传统SMC和改进方法的转速和转矩、电流
4 结 语
本文提出了一种基于新型滑模观测器的永磁同步电机无传感器控制策略。设计了一种新的滑模控制律,利用饱和函数代替传统的符号函数削弱了抖振,并利用模糊控制动态改变滑模增益Ksw,同时在电流控制环中采用二阶滑模控制器代替传统的PI控制,能够更准确地估计转子位置,并且有效抑制系统高频抖振,提高了系统的静态稳定性。

