感应电机损耗最小化预测控制策略研究

贺鸿彬,何 龙,颜秉洋,汪凤翔

(1.福建农林大学 机电工程学院,福州 350100;2.中国科学院海西研究院泉州装备制造研究中心,泉州 362216;3.福州大学 先进制造学院,泉州 362251)

0 引 言

感应电机(以下简称IM)具有经济性高、易于维护、体积小巧和耐用性强等优点,以感应电机为动力装置的驱动系统是工业领域的主流方案[1]。IM消耗的电能约占工业用电总量的60%,其运行效率与其负载密切相关,轻载工况下运行效率较低,因此长期处于轻载状态下的IM具有较大的节能空间[2-4]。

损耗模型控制(LMC)是一种基于电机参数建立损耗模型的节能算法,通过对损耗模型求解,得到损耗最小时的磁链来提升效率[5-7]。传统LMC具有简单、快速和不需要额外硬件等优点,但其高度依赖电机参数,因此在外部干扰过大时电机系统的性能将大幅下降。文献[8]采用模型参考自适应算法(MRAS)对模型参数的集总进行观测,重构电机损耗模型,解决了LMC参数依赖的问题,但其缺少对电流侧的优化,因此系统的动态性能较差。文献[9]采用遗传算法提高了电机的动态性能,并提出一种基于集成损耗模型的最优效率控制,该方案综合考虑了电机与逆变电路的损耗,但其算法过于复杂,要求较高的硬件支撑,不具备通用性。文献[10]提出一种自适应LMC方案,并用模型预测控制(MPC)提高系统动态性能,但其损耗模型未考虑铁损及漏感参数的影响。

针对上述问题,本文提出一种MRAS与连续控制集模型预测控制(以下简称CCS-MPC)相结合的效率优化策略。基于CCS-MPC的电流环控制器有效解决了传统PI控制抗干扰能力差、动态响应慢的问题。同时CCS-MPC具有算法简单和控制精度高的优势,较为贴合效率优化需求。采用MRAS对损耗模型中的定子电阻进行在线辨识,消除了电机运行发热导致参数失配的问题。最后,仿真与实验结果验证了所提算法的可行性和有效性。

1 考虑铁损的LMC策略

1.1 考虑铁损的IM模型

三相IM是一个复杂的非线性系统,传统损耗模型忽略铁损以简化模型结构。然而,铁损在实际系统中是客观存在的,简化模型将会产生较大误差,因此本文以IM转子磁场定向为算法基础,建立基于两相旋转坐标系的铁损电机动态模型,如图1所示。考虑到三相IM的转子漏感对电机控制影响较小,可将其忽略。为了更清楚地显示铁损与功耗之间的关系,使用等效铁损电阻RFe替代铁心损耗。

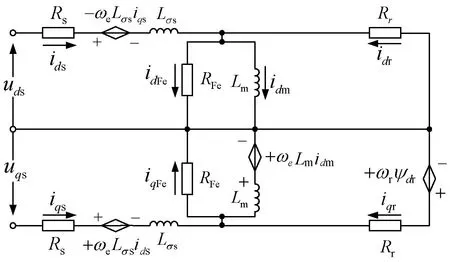
图1 转子磁场定向下的d-q轴动态铁损IM模型

图1中:id,qs,id,qr,idm,id,qFe分别为基于dq轴的定子电流、转子电流、互感电流和铁损电流;ud,qs,ωe,ωr,ψdr分别为输入电压、同步角速度、转子电角速度和转子磁链;Rs,Rr分别为定、转子电阻;Lm,Lσs分别为互感和定子漏感。

根据转子磁场定向特性,电机动态方程应满足以下条件:

(1)

结合上述条件,电机的电磁转矩方程如下:

(2)

结合图1,根据基尔霍夫电压、电流定律和上述条件,得到简化电机动态方程:

(3)

式中:TL表示负载转矩;p,J分别表示电机极对数和转动惯量;Rt表示电机转子电阻Rr和铁损等效电阻RFe的并联电阻。

1.2 基于LMC的效率优化

从图1能够得到以下关系式:

(4)

当电机处于稳态时,电流和磁链达到稳定,其变化率接近为零,因此式(4)中的微分项都为零,整理可得:

(5)

电机的损耗功率可以表示:

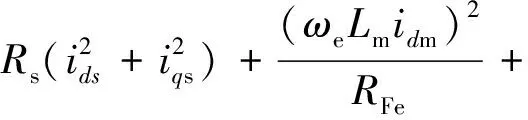
(6)

式中:ptotal,pcus,pcur,piron分别表示总损耗、定子铜损耗、转子铜损耗和铁损耗。

当电机达到稳态时,ωe和ωr保持稳定。此时,电机的总损耗将取决于ids,iqs和idm,又稳态时ids=idm,因此总损耗表达式可简化为:

(7)

其中,

(8)

电磁转矩的表达式可以简化如下:

(9)

损耗方程是一个典型的凹函数,必然存在一个ids使得总损耗最小。联立式(5)、式(7),求得总损耗关于ids的导数:

(10)

因此,损耗最小时的磁链值可以表示:

(11)

2 基于LMC-MPC的效率优化策略

2.1 电机定子电阻辨识

LMC算法高度依赖电机参数进行磁链计算,参数的变化将降低最优磁链的精度,为此,引入了MRAS对电机定子电阻进行实时观测,以提升LMC的参数鲁棒性,其结构如图2所示。

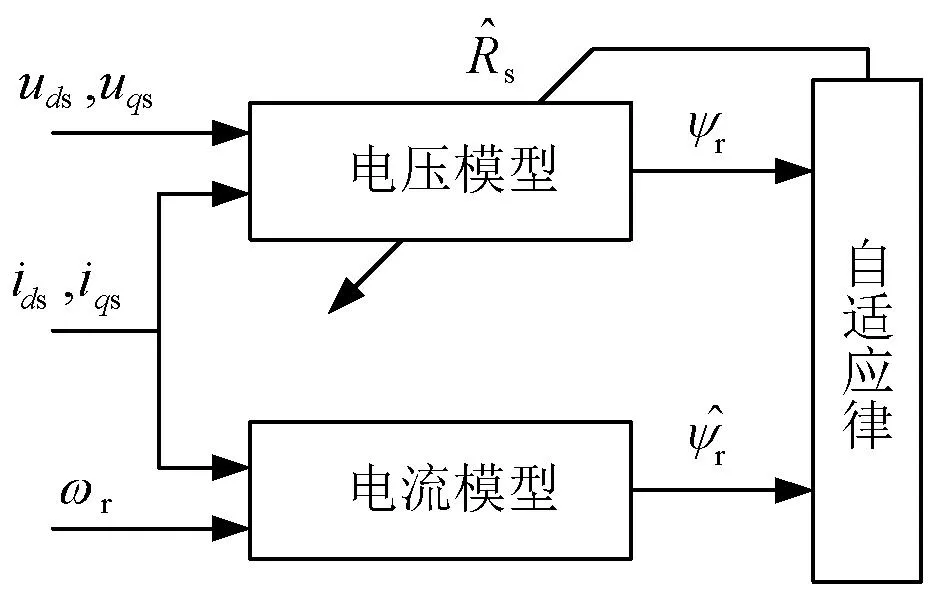
图2 MRAS算法框图

电压模型:

(12)

电流模型:

(13)

(14)

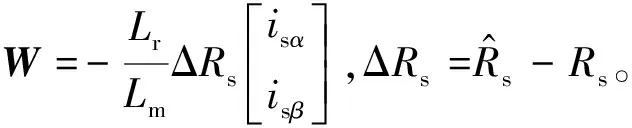
根据波波夫超稳定性理论,系统要达稳定须满足以下不等式:

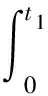
(15)

因此,可以得到下述自适应律:

(16)

为提高收敛性,引入了比例环节,最终定子电阻的辨识可以表示:

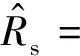
(17)

2.2 基于CCS-MPC的电流环控制器

效率优化算法的核心在于精确跟踪和控制转子磁链,因此控制器动态性能的优劣将直接影响效率优化算法的有效性。常规PI虽然能一定程度上满足控制需求,但由于鲁棒性差、控制参数复杂且难调,无法面对复杂工况。为此,设计基于CCS-MPC的电流控制器,CCS-MPC具有简单的工作原理、灵活的控制模式和强大的非线性约束适应性等优势,能够提供更高的稳态精度和更小的电流纹波,其算法结构如图3所示。

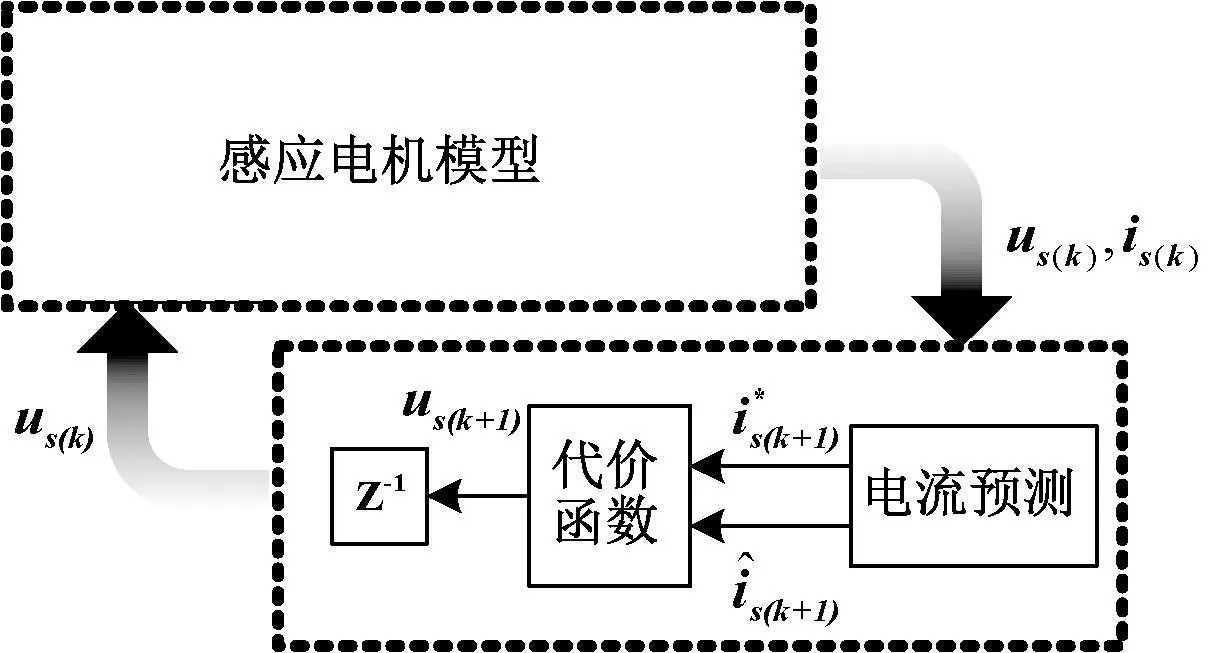
图3 CCS-MPC结构图

结合电机铁损模型,根据前向欧拉法,定子电流可以离散化为:

(18)

CCS-MPC的损失函数设计如下:

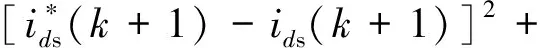
(19)

(20)

本文所提策略的控制框图如图4所示。其中外环为转速控制器和LMC算法;内环主为CCS-MPC。MRAS从电机获取反馈信号,辨识出定子电阻输入到LMC和CCS-MPC;LMC和转速控制器输出参考电流;CCS-MPC获取到反馈电流后,输出最优电压矢量;最后经过SVPWM和逆变电路转换为三相正弦电压。

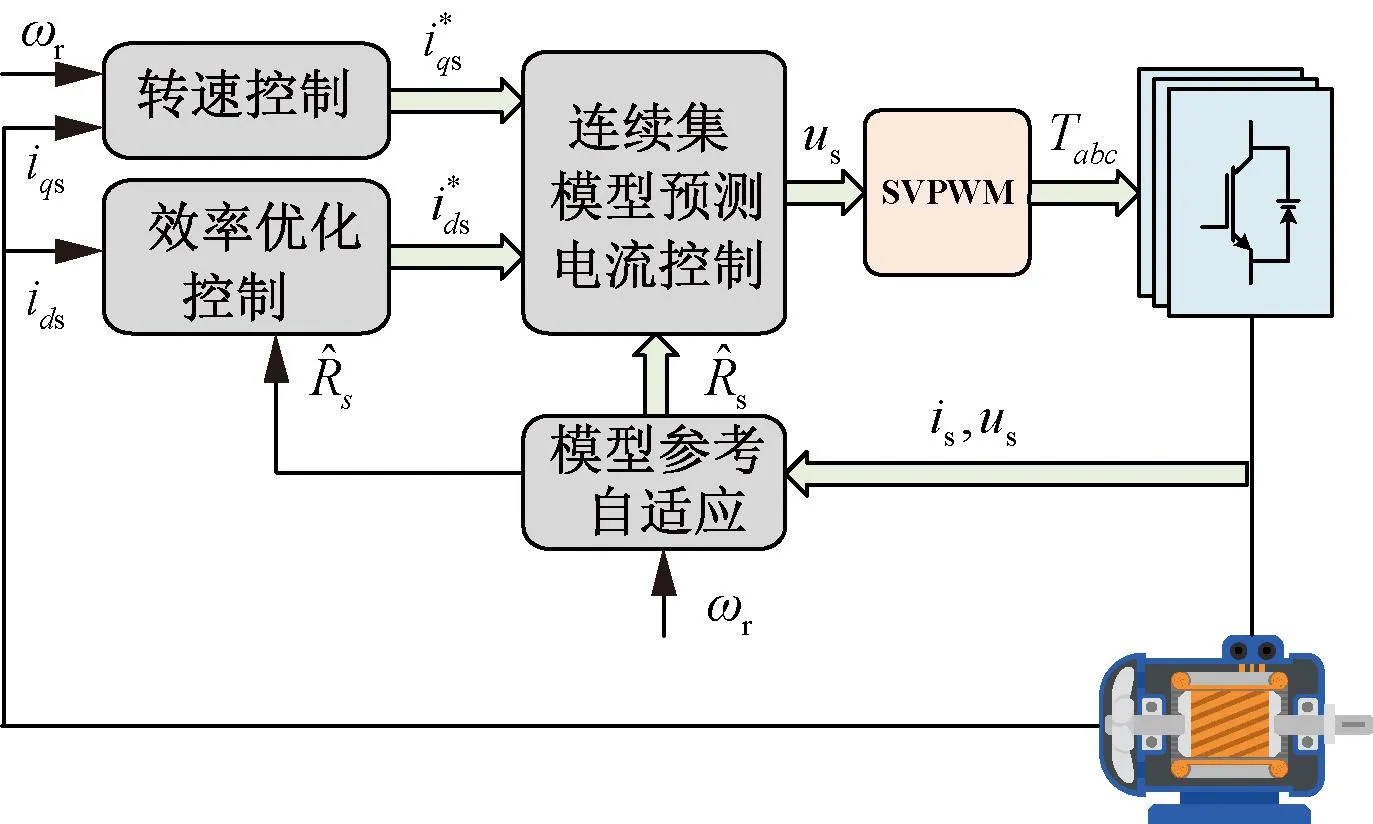
图4 LMC-CCSMPC结构图

3 仿真与实验

3.1 仿真结果

3.1.1 定子电阻辨识仿真

为验证所提算法对定子电阻辨识的有效性,搭建了基于铁损电机模型的参数辨识仿真,仿真结果如图5和图6所示。图5中:Rs-re,Rs-ob分别为实际电阻与辨识电阻。图6中:CM, VM分别表示电流模型与电压模型。

图5 Rs辨识结果

图5为电阻识别的结果,可以看出在电阻频繁变化时,控制算法仍能稳定跟踪,并且跟踪误差为±0.005 Ω。图6比较了参考磁通链和估计磁通链的轨迹,当系统稳定时,两者轨迹几乎重合。从仿真结果可知,所提算法能够有效辨识电机的实时电阻,具备提高LMC参数鲁棒性的功能。

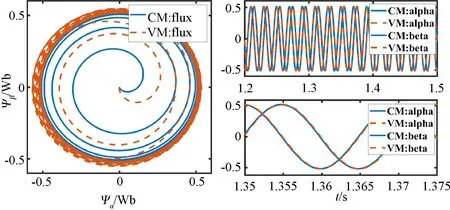
图6 参考磁链与观测磁链

3.1.2 基于LMC-MPC的效率优化仿真

在转速恒定的条件下,分别比较了LMC-MPC和LMC-PI两种算法的动态性能和效率优化效果。仿真条件为:在1 s时负载从2 N·m突变到4 N·m;2 s时再从4 N·m降回2 N·m;3.4 s时,加入效率优化算法。

从图7可知,负载为2 N·m时,LMC-MPC比LMC-PI效率提升16.7%,负载为4 N·m时,LMC-MPC比LMC-PI效率提升25.7%。

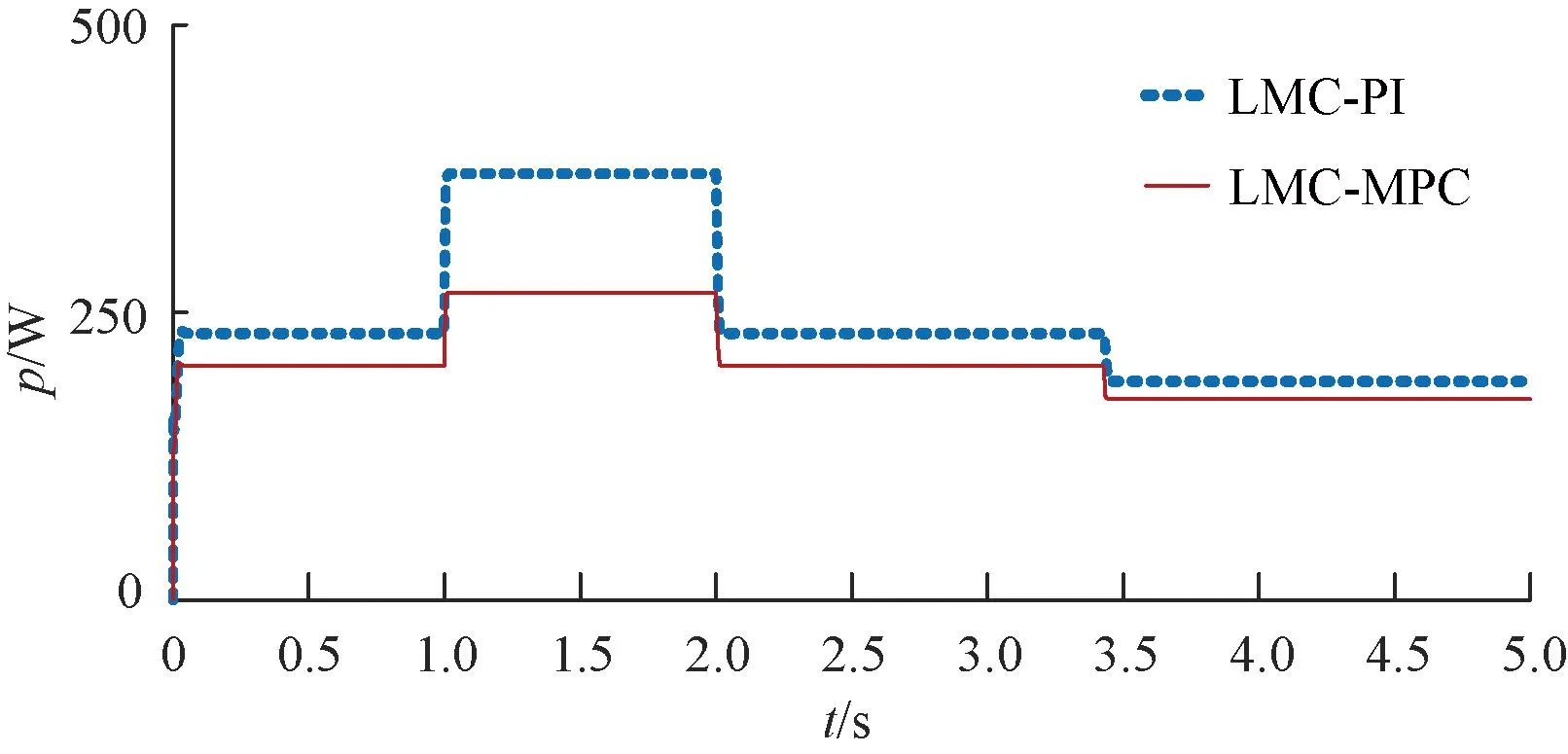
图7 损耗功率变化曲线

从图8可知,在负载突变时,LMC-MPC相较于LMC-PI具有更快的动态响应。因此,所提算法能够有效提高系统的动态性能和效率。

图8 转矩变化曲线

3.2 实验结果

为验证所提算法的有效性,搭建了三相IM效率优化对拖平台。该平台的采样频率和控制频率都为12.5 kHz,数字控制器采用FPGA&ARM芯片ZYNQ7000,实验电机的主要参数如表1所示。

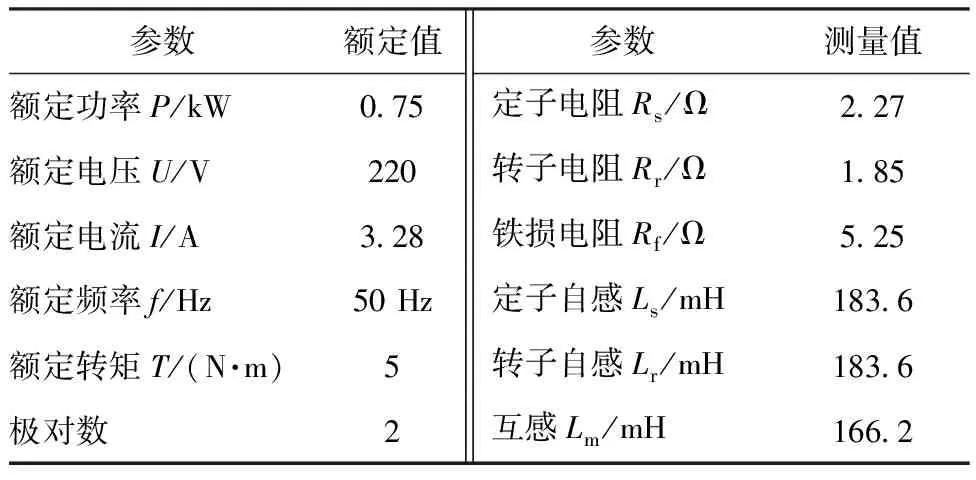
表1 感应电机平台参数

实验平台如图9所示,包含转矩转速分析仪、直流电源、功率分析仪、控制器、控制电机和对拖电机。其中对拖电机为三相永磁同步电机,采用某公司的CDHD变频器驱动。

图9 感应电机平台

3.2.1 正反转实验

为验证CCS-MPC算法在转速反转工况下的鲁棒性,就电机平台进行了实验,实验中转速从1 500 r/min突变到-1 500 r/min。实验结果如图10所示。

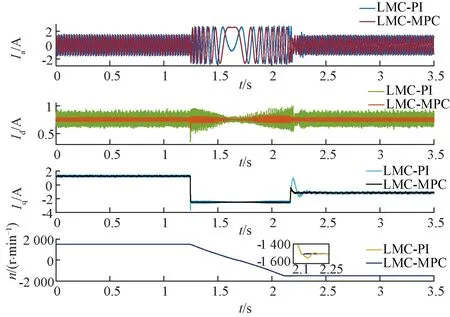
图10 反转实验图

图10中:Ia,Id,Iq,n分别是电机的A相电流、d,q轴电流和转速,电机转速在0.11 s处反转。

如图10,电机实测转速在1.25 s处开始反转,从电流及转速曲线可以得到,LMC-MPC相较于LMC-PI具有更快的动态响应,并且电流纹波更小、系统更稳定。

3.2.2 效率优化实验

为验证LMC-MPC算法的有效性,在不同转速下进行效率优化实验。实验带载1 N·m,转速分别为300 r/min和600 r/min,实验结果如图11、图12所示。

图11 转速600 r/min时效率优化

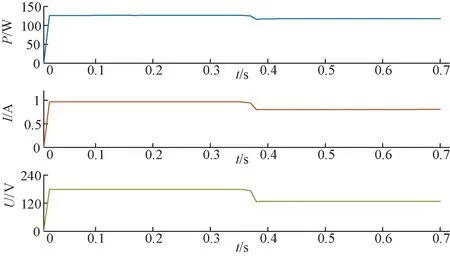
图12 转速300 r/min时效率优化

转速为600 r/min时,在时间为0.32 s处加入优化算法,电机功率从165.6 W降低到121.4 W,效率提高了约26.7%。转速为300 r/min时,在时间在0.37 s处加入优化算法,电机功率从132.5 W降低到103.1 W,效率提高了22.2%。实验结果表明,LMC-MPC有效地提升了电机的运行效率。

4 结 语

本文提出了一种LMC-MPC算法并应用于IM效率优化。该方案对传统效率优化控制进行了以下几项改进:

1)针对传统LMC不考虑铁损和漏感等问题,提出一种综合考虑各种损耗的LMC模型,实现了更好的节能效果。

2)LMC高度依赖模型参数,在面对复杂工况时,效率优化算法精度将严重下降,提出采用MRAS算法来辨识定子电阻,仿真结果表明,所提算法增强了LMC的参数鲁棒性。

3)针对传统PI动态性能差的问题,设计了一种基于CCS-MPC的电流控制器,实验结果表明所提算法能够提供更高的动态性能。