基于LSTM-UPF混合驱动方法的燃料电池寿命预测
曾其权,罗马吉,杨印龙,黄庆泽
(1中广核研究院有限公司,广东 深圳 518000;2武汉理工大学汽车工程学院,湖北 武汉 430070)
质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)作为一种新型的能源转换装置,具有对环境友好、启动速度快、工作温度范围广、能量转换效率高等优点,在未来有望大规模应用于交通运输行业和固定式发电装置中[1]。现阶段限制质子交换膜燃料电池商业化应用的因素有很多,包括氢气的获取成本偏高、储氢技术有待突破、加氢站基础设施偏少以及燃料电池的寿命需更长。其中燃料电池的寿命是制约其广泛运用的一个重要因素,美国能源部要求到2030 年,燃料电池的寿命需要达到25000 h[2],当电压降达到初始电压的10%即视为燃料电池老化失效。此寿命标准一方面提出了对燃料电池自身结构、材料及工况的要求,另一方面也是对燃料电池的运行与维护提出了要求[3]。
寿命预测是燃料电池预测与健康管理(prognostic healthy management,PHM)技术的重要组成部分[4]。准确预测剩余使用寿命(remaining useful life,RUL)有助于判断燃料电池的健康状态,可对其运行和维护提供指导性意见[5],保证燃料电池健康稳定地运行。对燃料电池RUL 预测已开展较多研究工作,如Liu等人[6]采用局部加权散点图平滑法对电压数据点进行平滑处理后,用长短时记忆神经网络(long short-term memory recurrent neural networks,LSTM RNN)算法进行稳态工况燃料电池寿命预测,发现该预测方法精度达到99.23%。Li 等人[7]为了克服数据有限条件下寿命预测精度较低的问题,提出了一种多输入单输出的双向长短时记忆神经网络,提高了有限数据下的预测性能,但训练时间和预测时间增加较多。Zhang 等人[8]采用离散小波变换(discrete wavelet transform,DWT)将燃料电池的电压时间序列转化为具有不同特征的子波形,然后利用高斯过程回归对这些子波形分别构建单独的预测模型,最后将预测结果进行叠加,发现预测结果具有较好的预测精度和鲁棒性。Sun等人[9]通过集成残差卷积技术、LSTM 单元和多头自注意力机制而提出一种新的燃料电池衰退预测模型,发现该方法的RUL 预测精度较高,而且预测时间不超过5 s。Jouin等[10]最早采用基于粒子滤波(particle filter,PF)的模型驱动方法来预测燃料电池RUL,预测时考虑了电池性能衰退状态的连续概率分布,但是此方法的预测误差较高。因为无迹粒子滤波(unscented particle filter,UPF)可以解决PF算法中存在的粒子退化现象,文献[11]通过建立二阶高斯退化模型完成基于UPF 算法的燃料电池RUL 预测,实现了很高的预测精度。Wang 等人[12]利用半经验模型的预测结果对数据驱动模型的输入进行修正来建立混合预测模型,有效改善了数据驱动模型在长期退化过程中预测结果的振荡性,该预测模型具有良好的误差分布和局部性能动态特性。Tian等人[13]提出了一种基于电压恢复模型和多核相关向量机结合贝叶斯优化的混合预测方法。贝叶斯优化可以对多核向量机训练模型的超参数进行优化,结合电压恢复模型实现对RUL 快速准确地预测,该方法的预测精度为95.35%且其泛化能力良好。
长短时记忆神经网络LSTM是单纯基于数据驱动的预测方法,其相较于普通循环神经网络解决了梯度消失的问题,且能够学习到时序数据中的模式和特征,这使得其在处理时间序列预测方面具有优势,但是直接使用LSTM来估计燃料电池RUL精度不佳,且不能提供良好的置信区间证明其可信度。随着数据驱动方法预测时间长度的增加,长期老化趋势预测的不确定性与误差将逐渐增加,会出现初始预测值漂移的问题,需要修正长期预测结果的初始值[14]。由于基于模型驱动的UPF算法对于非线性系统的拟合较好,且能够提供预测结果的概率密度分布[15],但是直接使用UPF算法对时间序列进行预测效果不佳。因此本工作结合LSTM和UPF算法的优点,提出了一种长短时记忆神经网络结合无迹粒子滤波(LSTM-UPF)的混合驱动预测方法对燃料电池RUL 进行预测,并使用法国FCLAB 实验室的稳态工况和准动态工况实验数据验证了此方法的可靠性以及对于不同工况的适应性。
1 实验数据
基于混合驱动方法进行寿命预测主要是为了结合基于数据驱动方法和基于模型驱动方法的优点,其中基于数据驱动方法的预测模型需要用到原始数据进行模型的训练。法国FCLAB 燃料电池实验室[16]在如图1 所示的测试实验平台上采用两个同一厂商生产的相同型号的燃料电池小电堆分别进行稳态和准动态老化实验研究。在老化实验中,实验平台在连续的实验时间中不间断监测氢气流量、空气流量、冷却液温度、冷却液流量等物理参量,同时确定这些物理参量可以保证燃料电池正常稳定运行,具体的运行参数如表1所示。

表1 FCLAB实验控制参量范围Table 1 Range of FCLAB experimental parameters controlled

图1 FCLAB实验平台[16]Fig.1 FCLAB Experimental platform[16]
稳态和准动态工况下进行实验的数据集分别命名为FC1和FC2。FC1是电堆在0.7 A/cm2的恒流工况下监测得到的数据,FC2是在工况为0.7 A/cm2的电流密度上增加了一个高频振动电流(频率5 kHz、幅值为±0.07 A/cm2)得到的实验数据。为了与燃料电池工作时电流密度剧烈变化的动态工况相区别,本工作将FC2的工况称为准动态工况。FC1和FC2的实验数据时间长度分别为1154 h 和1020 h,实验过程中以1 s 为时间间隔采集电压、电流、功率等24 种监测数据,但是这样测得的数据过多,质量较差,所以需要对原始数据以合适的时间步长为采样间隔进行重采样(一般选择1 h),并删除不良数据,以进一步提升数据质量。处理后的实验数据有利于加快计算的速度,也更有利于研究燃料电池的衰退过程。处理前后FC1 和FC2 的电堆电压随时间变化的数据如图2(a)和2(b)所示。
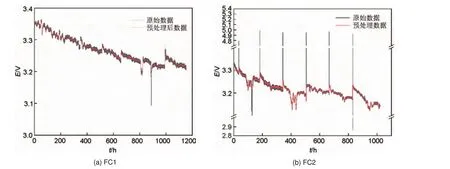
图2 处理前后FC1和FC2的电堆电压随时间变化数据Fig.2 FC1 and FC2 data before and after processing
2 相关算法原理
2.1 长短时记忆神经网络
LSTM 神经网络作为循环神经网络(recurrent neural network,RNN)的一种特殊形式,对RNN的隐藏层进行了改动,很好地缓解了RNN 数据之间的长期依赖问题,使其在处理长时间序列数据中具有更大的优势。LSTM由输入层、隐藏层和输出层构成,它在隐藏层创新性地引入了细胞概念和“门”结构,利用这个巧妙的结构,LSTM 可以选择性地记忆和遗忘一部分之前的相关信息。理论上讲,在较长的时间序列处理中,LSTM可以将处理信息一直传递,克服了只有短时“记忆”的缺陷,即使是很久远时间外的相关信息也可以传递到较后的时间中来。近年来,LSTM神经网络在语音文本辨识、寿命预测、故障诊断等众多领域被广泛应用,并取得了许多突破。
LSTM神经元包含三种门控单元和一些计算节点,“门”结构在计算过程中实现信息的添加与移除,LSTM 神经网络神经元结构图如图3 所示[17]。其中xt、ht为t时刻的神经元输入与输出,ct为神经元(储存单元)的状态,σ为激活函数。在t时刻,xt、ht-1一同输入神经元,遗忘门对两者进行计算,确定来自上一个时刻的细胞信息哪些需要遗忘。遗忘门计算如公式(1)所示[6]:
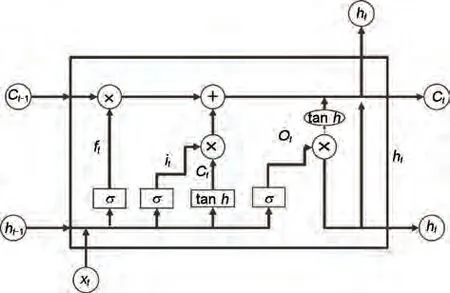
图3 LSTM神经网络神经元结构图Fig.3 LSTM Neural network neuron structure diagram
式中,Wf为遗忘门的权重矩阵,bf为遗忘门偏置向量。
输入门确定细胞状态中的哪些信息需要保留,分两步完成:首先确定需要更新的信息,然后创建新的这一时刻的状态。输入门计算公式如下:
式中,Wi为输入门权重向量,bi为输入门偏置向量,tanh为激活函数。
对式(2)与式(3)的结果进行线性处理可以得到这一时刻神经元的状态,如公式(4)所示:
最后,输出门确定神经元最终输出的信息,输出结果计算如下:
式中,WO为输出门权重向量,bO为输出门偏置向量。
2.2 无迹粒子滤波算法
粒子滤波是一种常用的近似贝叶斯滤波算法,它利用一群粒子集来表示结果的概率分布,采用的粒子数越多,算法估计结果越精确。传统的粒子滤波算法包括初始化粒子集、重要性采样、计算粒子权重、归一化权重、重采样等五个步骤。传统的粒子滤波算法有一个比较普遍的问题,即小部分粒子权重很大,而大部分粒子的权重已经小到可以忽略不计的程度。随着迭代次数的增加,大部分的计算资源就会浪费在计算那些微不足道的粒子上,这不仅导致计算成本的浪费,更有可能影响最后的估计精度。而无迹粒子滤波可以利用无迹变换优化建议密度函数,利用最新的观测信息来计算粒子的均值和方差,并用均值和方差来更新粒子。
在大多数情况下,PEMFC 的老化趋势都可以被认为是线性的,燃料电池的非线性只在其寿命结束的很少的一部分时间有所表现。因此,线性模型可以反映PEMFC性能衰退的基本趋势。同时在无迹粒子滤波(UPF)中可以采线性模型作为质子交换膜燃料电池的老化模型,相较于非线性模型这样可以减少计算成本并提高模型的可靠性。所采用的状态更新方程与观测方程如式(7)~(8):
式中,β是老化模型参数,vk为观测噪声,δk为噪声偏差范围。
2.3 离散小波变换
小波变换方法由短时傅里叶变换的思想衍生而来,它可以在不同尺度上对信号进行分解,将时间序列分解成多个子序列,解决了在频率多变条件下窗口大小不可变的问题。而相较于连续小波变换,离散小波变换(DWT)对时间序列的处理效果更好。在寿命预测研究中,DWT 将燃料电池时间序列分解为多个子序列,然后对多个子序列分别进行处理和预测可以有效提高预测结果的精度与鲁棒性[18]。
理论上,时间序列可以分解为无限个子序列,而考虑到计算的速度与成本,需要选择尽可能少的分解层数。j层分解后的低频率(整体趋势)系数a、高频率(细节)系数d和原始信号x的关系如式(9):
3 PEMFC混合驱动预测方法及结果
3.1 预测模型的构建
提出的LSTM-UPF 混合驱动预测方法流程如图4所示,主要包括两个部分。第一部分是基于长短时神经网络结构的长期老化趋势预测。在这一过程中,利用离散小波变换和漂移修正法对初始预测值的漂移现象进行修正。第二部分,针对模型驱动方法状态预测效果不佳的缺点,基于滤波算法的模型驱动方法不再对未来状态进行预测,而是直接利用第一部分得到的长期老化趋势对燃料电池的RUL进行估计。考虑到传统PF 算法的局限性,引入UPF 算法实现更精确的RUL 估计结果与高质量的预测置信区间。
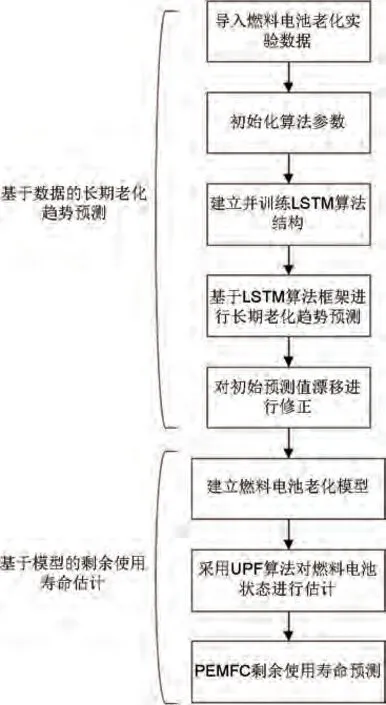
图4 寿命预测混合驱动方法流程图Fig.4 Flow chart of life prediction hybrid method
对于LSTM神经网络,较小的训练集和长期的时域预测会引起初始预测值漂移的问题。所以可以采用Zhang等[14]提到的漂移修正法对预测得到的电压进行修正,未来老化趋势预测的修正方法如式(10)~(11):
式中,N为预测集长度,Y为长期预测得到的电压序列,y为离散小波滤波之后的短期预测电压序列,Δ为修正因子,Ŷ为修正后的电压序列。经过漂移修正方法的应用,长期时域预测得到的燃料电池老化趋势可以用于估计PEMFC 的剩余使用寿命。
基于模型驱动的方法采用基于UPF 算法的模型来进行寿命预测,但是该模型驱动方法对长期预测精度效果较差。所以在该混合驱动方法中,UPF算法直接对基于数据驱动获得的未来老化趋势进行状态估计,不再利用模型状态函数进行电堆状态预测,由此避免模型方法预测精确度较差的缺点,发挥其自身优势。
3.2 模型参数设置
LSTM算法的主要配置如下:隐藏层的神经元数目设置为20,批大小设置为50,最大迭代次数为20,激活函数选择ReLU,损失函数选择平均绝对误差,优化器选择Adam,为了防止神经网络过拟合,Dropout设置为0.3。而对于基于模型驱动的UPF算法主要的参数设置粒子数N为100,假设状态初始值x0服从以电压初始值为中心的均匀分布。通过线性模型拟合电压初始值,可以得到公式(7)中β的初始分布范围为[0.001,0.005],观测噪声标准差范围为[0.00001,0.0001]。
3.3 预测结果分析
为了体现LSTM-UPF 混合驱动方法预测燃料电池寿命的效果,与文献[19]中分别采用基于模型的PF方法和UPF方法预测结果进行了对比。
针对稳态工况数据集FC1,电堆寿命终止可以设定为电压损失达到初始电压的3.5%,即电堆失效阈值为3.229 V,燃料电池的设定寿命为792 h。训练集采用0~550 h 的燃料电池实验数据,剩余使用寿命为242 h。FC1 的长期寿命预测结果如图5 所示,从图5 中可以看出,混合驱动方法的预测结果更加贴合真实电压,而PF 算法的预测结果偏离真实电压过多,UPF算法预测的电池电压老化趋势为线性老化,不符合电池实际老化,且预测精度不如混合驱动方法。混合驱动方法的RUL 预测结果为252 h,传统的PF 和UPF 方法的预测结果为136 h 和221 h,三种预测方法的RUL 预测误差分别为4.1%,8.7%和43.8%。混合方法预测的寿命终止点电压更接近真实寿命终止点电压,预测效果更好。
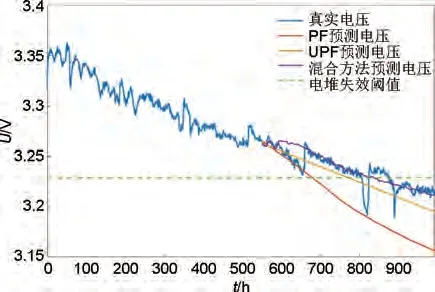
图5 数据FC1燃料电池电压预测曲线Fig.5 Fuel cell voltage prediction curve for data FC1
在同样条件下,采用混合驱动方法进行100次预测,得到的RUL频数分布直方图如图6所示,大部分预测结果位于246~247 h 和256~257 h,平均剩余使用寿命为252 h。由RUL频数分布直方图可得到寿命预测的置信区间宽度为11 h。
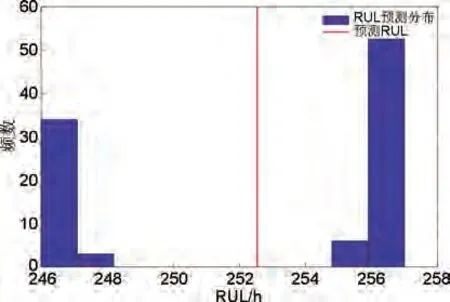
图6 数据FC1混合驱动方法RUL频数分布图Fig.6 RUL frequency distribution for hybrid method with data FC1
通过相关的算法评价指标(预测寿命终点、预测寿命误差、置信区间宽度、RUL 预测误差)来比较PF 算法、UPF 算法、混合驱动算法三种预测方法对FC1 的寿命预测效果,对比结果如表2 所示。可以看到,混合驱动算法的预测效果明显优于传统PF 算法,预测精度也比UPF 算法有所提升。与PF、UPF 预测结果相比,混合驱动算法的RUL 预测寿命误差降低了96 h、11 h。对比不同算法提供的置信区间,混合驱动算法计算最优建议密度分布函数将置信区间大大缩短,保证了燃料电池RUL预测结果的可靠性。

表2 稳态工况数据FC1不同预测方法的结果对比Table 2 Comparison of prediction results with different methods for steady-state operating data FC1
对于准动态工况数据集FC2,设置电堆寿命终止点为电压损失达到初始电压的5%,即电堆失效阈值为3.165 V,燃料电池的设定寿命为773 h。训练集选用0~510 h 的燃料电池实验数据,剩余使用寿命为263 h。数据集FC2的长期未来老化趋势预测结果如图7所示,对于FC2,三种预测方法的预测结果较FC1 有所改善,混合驱动方法、PF 方法和UPF 方法对于RUL 的预测结果分别为254 h、292 h 和228 h,RUL 的相对预测误差分别为4.1%、8.7%和43.8%。由此发现PF方法的预测结果偏差过大,UPF 和混合驱动方法的误差预测较小。混合驱动方法RUL频数分布图如图8所示,使用混合驱动方法得到的100个预测结果,大部分预测结果位于249~254 h 和264~266 h,平均剩余使用寿命为254 h。
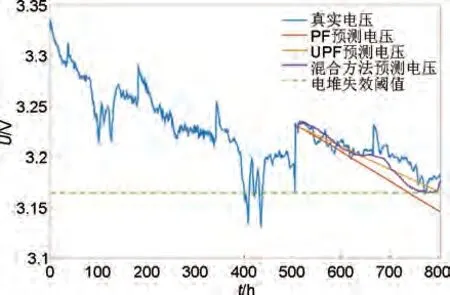
图7 数据FC2燃料电池电压预测曲线Fig.7 Fuel cell voltage prediction curve for data FC2
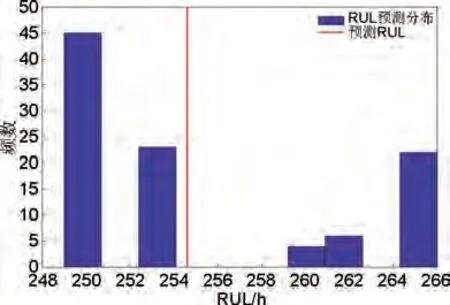
图8 数据FC2混合驱动方法RUL频数分布图Fig.8 RUL frequency distribution with hybrid method for data FC2
同样通过上述提出的评价指标对不同的预测方法进行预测效果评价,对比结果如表3所示。通过比较发现对于准动态工况,基于混合驱动方法的寿命预测的RUL 预测误差更小,预测误差分别降低26 h和20 h。对比不同预测算法的置信区间,发现在准动态工况下,混合驱动方法的寿命预测结果置信区间较小,可靠性较高。

表3 准动态工况数据FC2不同预测方法的结果对比Table 3 Comparison of prediction results with different methods for quasi-dynamic operating data FC2
Zhang 等[14]采 用LSTM 或者改进LSTM 的方法进行寿命预测,这些方法仅用于短期的寿命预测。本工作所使用的混合预测方法可用于燃料电池的长期预测,应用场景更广泛。Benaggoune 等[20]采用变步长LSTM方法进行燃料电池长期寿命预测,但是其并未结合模型驱动的方法,这使得其遇到准稳态工况时预测精度较差。因此,与单纯基于模型和数据驱动的方法相比,融合方法提高了长期退化预测的精度和工况适应性。
4 结 论
针对质子交换膜燃料电池寿命预测的问题,本工作采用一种长短时记忆神经网络结合无迹粒子滤波的混合驱动方法来进行燃料电池的寿命预测。采用离散小波变换技术对实验数据处理和漂移修正法对LSTM 神经网络的预测结果进行修正,得到PEMFC 的长期未来老化趋势。然后利用无迹粒子滤波方法直接对数据驱动获得的未来老化趋势进行状态估计,进一步提升了燃料电池剩余使用寿命的预测精度。本工作将此算法应用于稳态与准动态工况下老化的燃料电池寿命预测中,对于这两种工况下老化的燃料电池,使用混合驱动方法对其RUL预测相对预测误差为4.1%和3.4%,置信区间宽度分别为11 h和16 h,表明混合预测方法的预测误差及可信度较好,工况适应性良好。
由于本工作所使用的工况仅限于稳态与准动态工况,并未根据相关的循环标准设计动态工况进行老化实验。所以并未对动态工况下老化的电池进行寿命预测。后续应根据动态工况下的老化实验数据研究该混合驱动方法的普适性。

