基于射线追踪方法的电离层点对点传播问题研究

李佳文 李慧敏 郭立新 江晓丽

（西安电子科技大学, 西安 710071）

0 引 言

短波通信借助了电离层对短波的折射和反射，是唯一不受网络枢纽和有源中继制约的远程通信手段。可以使用射线追踪技术来研究短波通信的传播轨迹，主要有解析射线追踪和数值射线追踪[1-2]。解析射线追踪虽然计算速度快，但要求忽略地磁场的影响，而数值射线追踪可解决该问题。20世纪70年代Jones等人[3]开发了三维数值射线追踪程序，其一直被广泛使用。柳文等人[4]运用三维数值射线追踪求解了分段准抛物(quasi parabolic segments, QPS)电离层模型中的射线轨迹，并解决了工程应用中的传播问题。孙方等人[5]利用基于费尔马原理的射线微分方程，采用直线几何近似和变步长技术相结合的快速算法实现了电离层短波射线追踪。侯维君等人[6]选用国际参考电离层(International Reference Ionosphere, IRI)模型以及国际地磁参考场，实现了电离层短波的三维数值射线追踪。在使用射线追踪技术研究短波传播问题时，如何真实地表征电离层电子密度也是研究的重点之一。一般要根据不同的应用需求来选取电离层模型。

1968年，Croft等人[7]提出了准抛物(quasi para bolic, QP)电离层模型，此模型在不考虑地球磁场的影响下，可以找到球对称电离层的射线路径的解析解，但事实上从电离图和非相干散射雷达等导出或测量出的电子浓度剖面发现实际电离层并不是简单的QP形状。随后，Dyson 和 Bennett 提出QPS电离层模型[8]，其是QP模型的一种改进模型，比QP模型能更为精确地描述电离层情况，且可以通过解析方法来求解电离层参数。因此，近年来被广泛应用于工程实践中。但是，QPS电离层模型也只适用于描述相对简单的电离层条件，对精度要求较高的应用是不合适的。IRI模型是由国际无线电科学联盟(International Union of Radio Science，URSI) 和空间研究委员会 (Committee for Space Research, COSPAR)联合工作组开发并一直改进和更新的一种经验模型[9]，其是根据大量的地面观测资料和多年累积的电离层研究成果建立起来的，是目前国际上应用最广的电离层经验模型。该模型提供从地面60～2 000 km高度的电子密度、电子温度、离子密度、离子成分等电离层参数的月平均值，可以较好地反映电离层的平均状态，但其计算复杂度较高。随着计算机技术的发展，目前IRI模型在短波通信中被大量应用，以提高短波通信的可靠性。综上，电离层模型本身的精度会对射线路径造成较大的误差，从而对短波通信中精度要求较高的应用有重大的影响。而电离层模型的高精度要求会导致模型的复杂度提高，影响其应用计算的效率。如何选择合适的电离层模型满足不同情况下的应用需求是本文研究的重点。

众所周知，短波通信和电离层斜向探测本质上都属于点对点传播问题，即固定收发站之间的传播问题。固定收发站的高频短波传播需要使用射线追踪自导引技术确定发射机的发射仰角方位角，使射线可以准确投射到接收机位置[10-12]。Nickisch[13]采用单纯形法进行三维点对点射线追踪。曾中超等人[14]以IRI模型2007版以及国际参考地磁模型第11版为背景进行了点对点传播仿真，实现了低角射线、高角射线以及不同层反射的射线的搜索，并与实测数据进行对比。基于变分方程，曾中超等人[15]对牛顿自导引算法进行改进，提高了自导引计算的收敛速度。由于点对点传播模型的算法基础是射线追踪，因此点对点传播模型的准确性和稳健性也受电离层模型的影响。

本文将研究两种不同电离层模型-QPS电离层模型和IRI模型下的点对点传播问题。首先，用QPS模型来拟合IRI模型下的电子密度，然后运用龙格-库塔算法数值求解Haselgrove方程[16]，最后利用牛顿自导引算法实现点对点传播，并比较两种模型下点对点传播算法的稳健性和精确性。

1 电离层模型

1.1 QPS模型

QPS电离层模型的电子密度剖面表达式为[8]

以上为QPS模型，其可以构建出E、F1、F2层的电子密度剖面。一般情况下E层的底层高度在距离地面90 km左右，所以本文使用QPS模型模拟的是距离地面90～400 km高度的电子密度分布。

1.2 IRI模型

IRI模型[17]将电离层的电子密度分为六个子区域，包括顶部、F2层部、F1层、中间区域、E层和D区域。

1.3 QPS拟合IRI模型给定的电子密度

为了研究QPS和IRI两种模型对点对点传播模型的影响，本文在90～400 km高度处使用QPS模型对IRI模型给定的电子密度进行拟合，使其最大峰值处的电子密度基本一致。选取作为背景电子密度的IRI模型，其输入经纬度为(134.774 036°E，26.144 105°N)，高度范围为90～400 km。得到不同时间下QPS模型的拟合结果如图1所示。

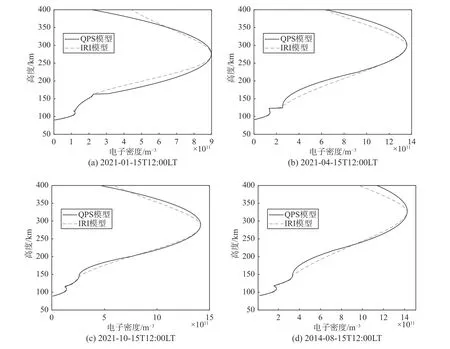
图1 不同时间下QPS模型拟合IRI模型电子密度的结果Fig.1 Results of QPS model fitting IRI model electron density at different times

本文考虑了不同年份以及不同季节的电离层电子密度，选取的时刻均为正午12:00时分。由图1可以看出冬季电离层的电子密度要明显小于其他季节，这主要是由于冬季太阳辐射强度较弱导致电离层的电离程度弱于其他季节。

不同时期QPS模型拟合IRI模型的误差如表1所示，其均方根误差均小于8×1010m-3，平均绝对百分比误差均小于15%，拟合结果较为准确。且由图1可以看出，所选取的四个时间下，在90～150 km的高度处，也即电离层E层所在高度处，QPS模型拟合IRI模型电子密度剖面的效果均较好，但在更高的高度也即F层拟合效果不如E层。本文选取的短波频段的反射高度主要在E层，所以可用IRI给定的及QPS拟合的电子剖面图分别进行点对点射线追踪，并比较其结果以及误差。

表1 四个时间下的拟合结果误差对比Tab.1 Error comparison of fitting results under the four times

2 点对点射线追踪

2.1 方法原理

点对点传播模型的基础是射线追踪算法，而射线追踪算法主要是求解Haselgrove方程。在球坐标系下，以电波传播群路径P′为参数的Haselgrove方程为

式中：r、θ、φ为射线路径上的点在球坐标系下的坐标；kr、kθ、kφ为波矢量在球坐标系下的三个分量；c为光速。式(2)中前6个方程用于计算在球坐标系下射线路径上点的坐标以及在此点的波矢量。最后一个方程为时变介质中电磁波的频率漂移，由于电离层的时变性造成的频率漂移量很小，所以在射线追踪过程中每一步不需要调整频率。

Haselgrove方程引入的哈密顿算符H与波矢量、相折射指数n的关系为

在考虑地磁和碰撞的情况下，折射指数为[18]

对于高频电磁波，碰撞系数Z一般非常小，可以忽略，忽略碰撞系数后折射指数可以表示为

若既不考虑地磁场的影响，又不考虑碰撞的影响，寻常波的折射指数可以进一步简化为

上述Haselgrove方程组可以利用龙格-库塔算法进行数值求解。群路径每变化一个步长就可以得到射线路径点的位置坐标以及波矢量，最终即可得到完整的射线轨迹[19-21]。

为了实现精确的固定收发站的射线传播，需要自导引技术，即通过对射线的发射仰角、方位角进行搜索，使得射线能被固定接收站接收。本文采用牛顿算法来实现自导引，其需要求得以下非线性方程组：

式中：θr和φr分别为接收点的球坐标；α和β分别为发射点电波发射的方位角和仰角，可以采用牛顿法来进行求解，表达式为

通过以上算法，进行牛顿算法的一次次迭代即可实现三维射线点对点传播，找到精确到达接收站射线的初始仰角和方位角。

2.2 两种电离层模型下的点对点传播结果对比

点对点传播的仿真参数设置如下：时间为2021-01-15T12:00，发射站经纬度为(134.774 0°E，26.144 1°N)，接收站经纬度为(123.264 2°E，24.574 6°N)，收发站之间的地面距离为1 169.215 9 km。本文主要讨论O波在两种不同电离层模型下，不同射线工作频率下点对点传播模型的误差精度和稳定性随迭代步长的变化。

表2给出了入射波的频率为9.79 MHz、射线追踪迭代步长分别为10-4km和10-3km时，点对点传播模型在两种不同电离层模型下的初始设置。其中，QPS模型在不同迭代步长情况下的初始仰角设置都有2个，这是由于固定链路的短波传播存在多径效应。

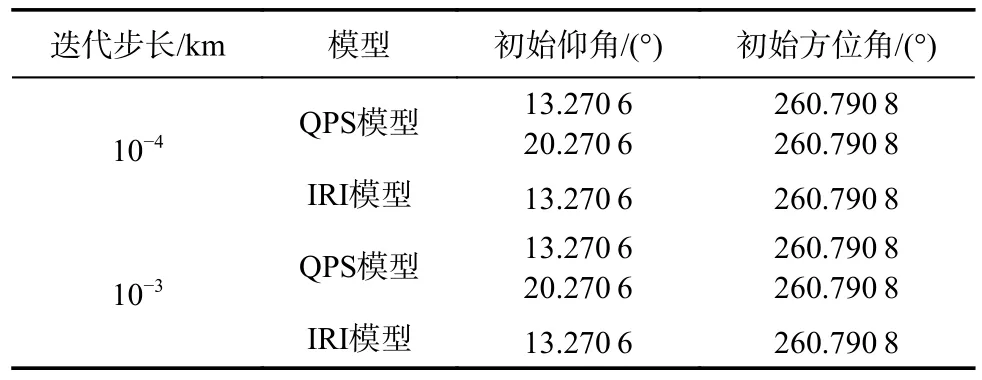
表2 2021-01-15T12:00LT点对点初始条件(f=9.79 MHz)Tab.2 Point-to-point initial conditions at 2021-01-15T12:00LT (f=9.79 MHz)

图2给出了入射波频率为9.79 MHz、射线追踪迭代步长分别为10-4km和10-3km时，两种不同模型下点对点传播模型的地面距离误差随迭代次数的变化。此时的初始仰角都设置为13.270 6°，方位角都设置为230.790 8°。从图2(a)可以看出，在射线追踪的迭代步长为10-4km下，相同迭代次数时QPS模型的地面距离误差远大于IRI模型的，且经过7次迭代后IRI模型下的地面距离误差几乎接近于0，而QPS模型下的地面距离误差在第6次迭代以后趋于平稳，其地面距离误差为10-4～10-3km。说明在迭代步长为10-4km 时，IRI模型下点对点传播模型的精度要高于QPS模型。从图2(b)可以看出，在射线迭代步长为10-3km下，相同迭代次数时QPS模型的地面距离误差大都大于IRI模型的，IRI模型的地面距离误差在第5次迭代之后趋于稳定，约为10-3km，大于迭代步长为10-4km稳定时的误差。而QPS模型的地面距离误差在第8次迭代时很小，但并不稳定，随着迭代次数的增加，在第10次迭代后趋于稳定，误差集中在10-2km左右。由此可知，迭代步长越小时，两模型下的点对点传播模型精度越好，且达到稳定误差时的迭代次数越小，但程序的运行速度越慢。

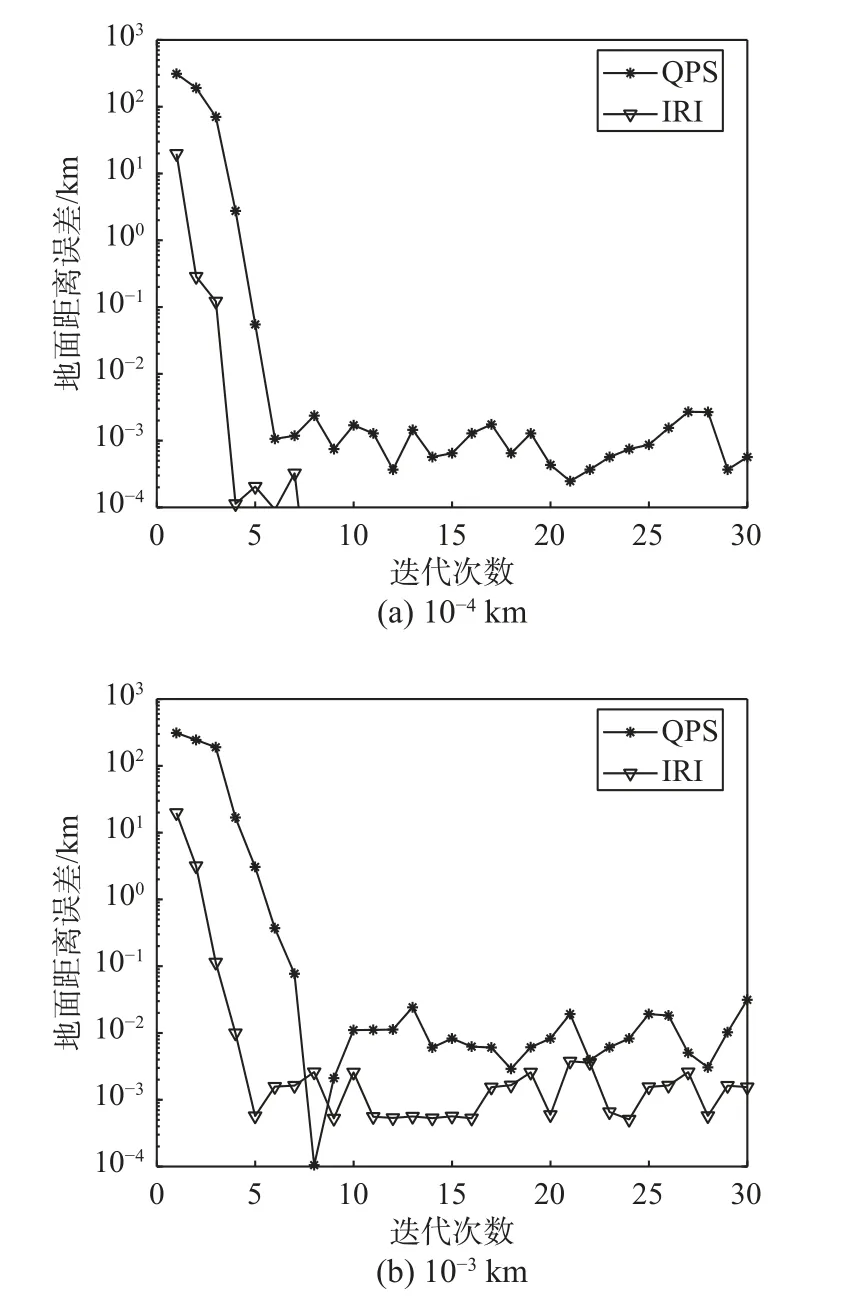
图2 2021-01-15T12:00LT f=9.79 MHz时不同迭代步长两模型下点对点射线追踪地面距离误差随迭代次数的变化Fig.2 Point-to-point ray tracing ground distance error varies with the number of iterations under the two models at 2021-01-15T12:00LT (f=9.79 MHz)

如表2所示，QPS模型下点对点传播模型有2条射线路径。图3给出了QPS模型下不同迭代步长的射线二维传播路径图，可以明显看到这条固定链路在QPS模型下会有两条传播路径。在迭代步长为10-4km时，一条路径的仰角为7.055 5°，方位角为263.919 2°，反射高度为94.945 8 km，在E层底部；另一条路径的仰角为18.280 3°，方位角为263.913 1°，反射高度为144.934 7 km。在迭代步长为10-3km时，一条路径的仰角为7.055 6°，方位角为263.919 2°，反射高度为94.945 8 km，在E层底部；另一条路径的仰角为18.280 2°，方位角为263.913 1°，反射高度为144.934 9 km。我们可以发现相同电离层模型情况下，不同迭代步长主要影响点对点传播模型中的发射仰角和反射高度，但是都相差不大，仰角差值约为0.000 1°，反射高度差值约为0.000 1 km，在工程应用中一般可以忽略。

图3 2021-01-15T12:00LT f=9.79 MHz时不同迭代步长QPS模型下的点对点射线追踪多径Fig.3 Point-to-point ray tracing multipath under the QPS model at 2021-01-15T12:00LT (f=9.79 MHz)

当射线工作频率为14.23 MHz时，点对点传播模型的初始仰角、方位角设置和频率为9.79 MHz时一样，见表3。此时，QPS模型不存在多径效应。当迭代步长分别为10-4km和10-3km时两种不同模型下点对点射线追踪地面距离误差随迭代次数变化如图4所示。由图4(a)可以看出：在最初的几次迭代过程中QPS模型下与IRI模型下的地面距离误差相差不大；随着迭代次数的增加，经过8次迭代以后，IRI模型的地面距离误差稳定在6×10-6km，QPS模型稳定在10-5～10-4km。当迭代步长为10-4km时IRI模型下的点对点传播模型的精度和稳定度都高于QPS模型。由图4(b)可知，IRI模型下经过5次迭代后其地面距离误差趋近于5×10-4km，较为稳定，而QPS模型经过7次迭代后地面距离误差在10-4～10-2km波动，波动较为明显，进一步验证了IRI模型下的点对点传播模型的精度和稳定度都高于QPS模型。另外，明显看出，迭代步长越小时，IRI模型下的地面距离误差越大。

表3 2021-01-15T12:00LT点对点初始条件(f=14.23 MHz)Tab.3 Point-to-point initial conditions at 2021-01-15T 12:00LT (f=14.23 MHz)

图4 2021-01-15T12:00LT f=14.23 MHz时不同迭代步长两模型下点对点射线追踪地面距离误差随迭代次数的变化Fig.4 The ground distance error of point-to-point ray tracing with the number of iterations under the two models at 2021-01-15T12:00LT(f=14.23 MHz)

不同射线工作频率、不同迭代步长、不同电离层模型情况下的点对点传播模型的射线追踪结果如表4所示。由表4可知，相同条件下QPS模型的点对点射线追踪平均迭代一次程序运行所需时间要小于IRI模型，并且当迭代步长从10-4km增加到10-3km时IRI模型平均一次迭代所需时间减少到原来的1/10左右，而QPS模型平均每次迭代所需时间减少到原来的1/36左右。即不仅QPS模型下点对点射线追踪运行速度要远大于IRI模型，且增大迭代步长时QPS模型下点对点射线追踪的运行速度会有比IRI模型更大程度的提高。但在精度方面，QPS模型远不如IRI模型下点对点射线追踪的精度高，尤其是在10-4km的迭代步长情况下二者的精度差距很大。

当射线的工作频率为9.79 MHz时，QPS模型和IRI模型下射线反射高度都在E层，且在QPS模型下有多径效应，IRI模型下没有多径效应。而当射线的工作频率为14.23 MHz时，IRI模型下射线的反射高度处在电离层的F层。此外，当射线的工作频率为14.23 MHz时两模型下每次迭代平均运行时间都要大于9.79 MHz，可能是因为入射频率越高，射线的反射高度更高，需要计算的路径也越长，导致了运行时间的增加。

为了进一步研究两种模型下点对点射线追踪结果随迭代步长的变化，比较了2021-01-15T12:00LT两种不同电离层模型下，初始仰角和方位角一致时，工作频率为9.79 MHz的点对点传播模型程序的运行时间以及地面距离误差随迭代步长的变化，结果如图5所示。

图5 2021-01-15T12:00LT f=9.79 MHz两模型下点对点射线追踪运行时间和地面距离误差随迭代步长变化Fig.5 The running time and ground distance error of pointto-point ray tracing varies with the iteration step size under the two models at 2021-01-15T12:00LT( f=9.79 MHz)

由图5(a)可知：当迭代步长较小时，IRI模型的点对点射线追踪程序运行时间远大于QPS模型；随着迭代步长的增大，IRI模型与QPS模型程序运行时间相差逐渐减小，且逐渐趋于平稳。表明当迭代步长增大到一定值时，再增大迭代步长对程序的加速作用并不明显。

由图5(b)可知：在迭代步长较小时QPS模型下的点对点射线追踪地面距离误差与IRI模型差别不大；随着迭代步长的增大二者地面距离误差之间的差别逐渐增大，且QPS模型下点对点射线追踪的地面距离误差值总是大于相同迭代步长情况下IRI模型，表明IRI模型下与QPS模型下的点对点传播模型相比具有更高的精度。当迭代步长进一步提高时二者的地面距离误差值又差别不大，此时两模型下的点对点射线追踪结果的误差都很大，并且随着迭代步长的进一步提高，开始出现点对点射线追踪无法收敛的情况，说明不能无限制地提高迭代步长来加速程序。

综上所述，根据工程需求，在迭代步长较小时可以选择QPS模型进行点对点射线追踪提高程序运行速度；当迭代步长较大时可以选择IRI模型进行点对点射线追踪提高计算精度，但迭代步长不能过大，否则射线无法准确到达接收站。

2.3 时延验证

为了验证射线追踪算法的准确性，可以将射线追踪仿真群时延和实测群时延进行对比，但是一般情况下实测群时延数据不容易获得。为了实现验证的目的，可用另一种方法替代实测群时延[22]。本文使用虚拟群时延tvirt代替实测时延，如图6中所示，其可用tvirt=ACB/c求得，其中ACB为直线AC和CB的长度之和。图中，β为射线的发射仰角，RT为地球半径，

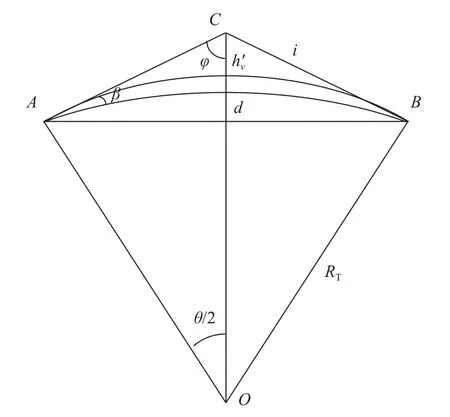
图6 射线追踪轨迹和虚拟轨迹示意图Fig.6 Schematic of ray tracing trajectory and virtual trajectory

选取2021-01-15T12:00LT的电子密度，射线追踪迭代步长为10-4km，QPS模型以及IRI模型下虚拟时延和射线追踪群时延随射线频率的变化结果如图7所示[23]。

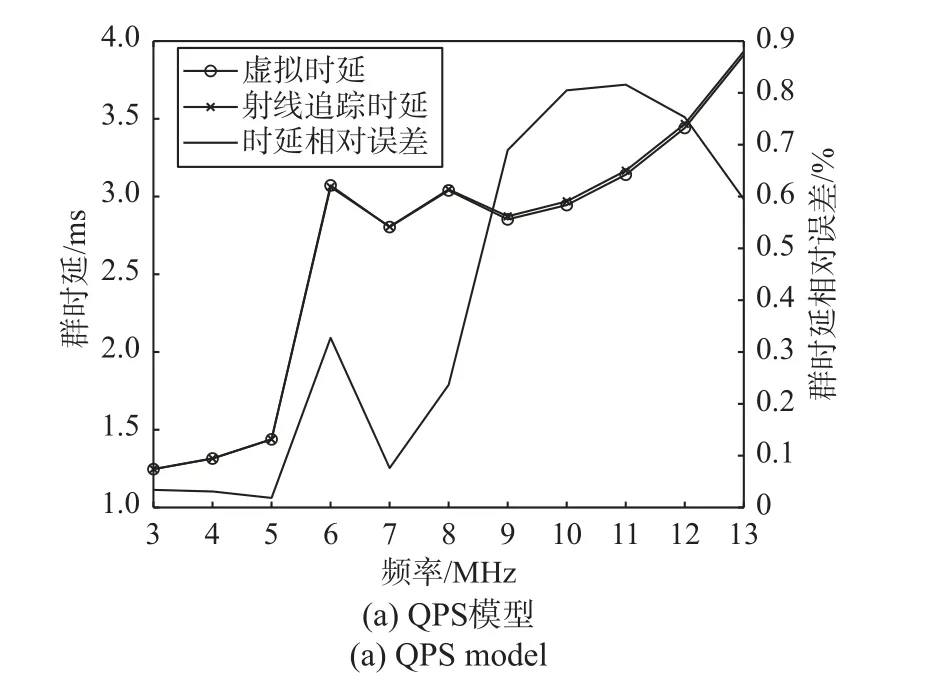
图7 两模型下虚拟时延与射线追踪时延对比Fig.7 Comparison of simulation delay and ray tracing delay under two ionospheric models

由图7可知两电离层模型下的群时延相对误差均小于1%，验证了两电离层模型下射线追踪算法的准确性。

3 结 论

针对点对点模型算法的稳健性和精确性问题，本文讨论了不同电离层模型(QPS和IRI模型)下的点对点传播问题。结果发现，在两个模型下均可实现固定链路的追踪，且在QPS模型下出现了多径效应。由此，可知电离层模型对点对点传播的路径有很大影响。另外，我们发现， IRI模型下的点对点射线追踪更容易达到稳定。在迭代步长较小时，QPS模型速度更快，而在迭代步长较大时，IRI模型下的射线追踪精度更高。通过虚拟群时延验证，进一步确认了射线追踪模型的准确性。

本文只考虑了均匀电离层情况下的点对点射线追踪问题，后续须对非均匀电离层情况下的点对点射线追踪问题进行研究。

致谢：本研究工作得到西安电子科技大学高性能计算校级公共平台的支持。