基于混合蒙特卡洛/多项式混沌展开方法的多参数随机等离子体不确定性分析

刘江凡 刘晓妹 李铮 焦子涵 徐聪 席晓莉

（1.西安理工大学, 西安 710100；2.中国运载火箭技术研究室空间物理重点实验室, 北京 100076）

0 引 言

由于电磁模型的复杂性不断增加，需要对直接影响输出响应量的不确定性进行量化和分析。对于此类分析，多项式混沌展开(polynomial chaos expansion, PCE)方法已经展示出了相当大的潜力，有望替代耗时的蒙特卡洛(Monte Carlo, MC)方法。PCE方法的有效性已经在各种数值仿真中得到了验证，在这些仿真试验中，具有少量随机变量输入的随机输出响应量可以通过少量多项式展开项充分逼近[1-4]。然而，随着随机变量维数的增加，在相同的多项式总阶数D下，展开项的数量迅速增加。例如，D=1,2,3时，有2个随机输入变量的PCE模拟，分别需要3，6，10个多项式展开项。相比之下，对于相同的总阶数D，具有10个随机变量的模拟需要11，66和286个展开项。随着随机变量数量的快速增长，多项式展开项的数量迅速增加，会显著降低PCE方法的效率。目前已有的比较成熟的减少PCE项以及所需样本个数的方法主要有稀疏多项式混沌法[5-8]和稀疏节点法[9-11]。

为克服多参数PCE模拟所产生的巨大计算成本，我们采用一种混合MC/PCE方法[12-14]，该方法是一种使用已知近似随机函数的特殊方法。由于传统的MC方法通过简单地增加迭代次数或者降低随机变量的标准差σ来提高计算结果估计的精度，σ越小，计算结果的精度越高，但是计算成本过高。因此，在本文中，使用非侵入式多项式混沌(nonintrusive polynomial chaos，NIPC)方法得到相对应的近似随机函数，并与少量MC方法联合仿真，从而达到多次MC模拟结果的精度。同时基于回归法的PCE方法不使用越来越高的多项式阶数来提高精度，避免了大量的多项式展开项数，从而达到缓解“维数灾难”问题的目的。该混合方法不需要MC的大量样本，同时提高了低阶多项式混沌方法的计算精度，降低了计算复杂度，节约了时间和成本。

在本文中，将混合MC/PCE方法应用于一维电磁波传播问题中，即平面波入射非均匀分层等离子体平板，每一层的等离子体电子密度相互独立且服从高斯分布；并利用该模型来验证所提出的混合MC/PCE算法的准确性和计算效率。

1 PCE方法

1.1 多项式混沌基础

多项式混沌法起源于Wiener各项同性混沌理论中的随机变量谱展开[15]。近年来，PCE方法被广泛应用于不确定性分析问题中。多项式混沌方法是一种基于不确定性谱表示的随机方法。谱表示不确定性的一个重要方面是可以将随机函数分成确定成分和随机成分。例如，对于随机媒质电磁散射问题中的任何随机函数(即α∗)，如雷达散射截面、透射系数等，混沌多项式理论下输出响应可表示为p阶截断的混沌多项式模型[14]：

式中：αi(x)为待求的混沌多项式展开系数；ψi(ξ)为由随机变量的分布函数ξ确定的正交多项式基函数的第i项展开项。假设α∗是确定性自变量向量x和n个独立随机变量的向量ξ=[ξ1,···,ξi,···,ξn]的函数，ξ的分布函数类型由文献[16]给出。

本文随机变量被定义为高斯分布，则对应的多项式是厄米特(Hermite)多项式，展开项数P与Hermite多项式最高阶d的关系为

式中，n为随机变量的数量。可以看出，只有1个随机变量时，展开项数P和多项式最高阶d是相等的，即P=d。表1给出了只有1个随机变量且多项式最高阶d=4的PCE基函数。而有两个及两个以上数量的随机变量时，展开项数P会成倍增加。例如，如果有3个随机变量，多项式最高阶d={1,2,3}时，展开项数为{4,10,20}。表2为总阶数d=2和3个随机参数的PCE基函数。

表1 总阶数d=4和1个随机参数的PCE基函数Tab.1 PCE basis function with total order d=4 and one random parameter

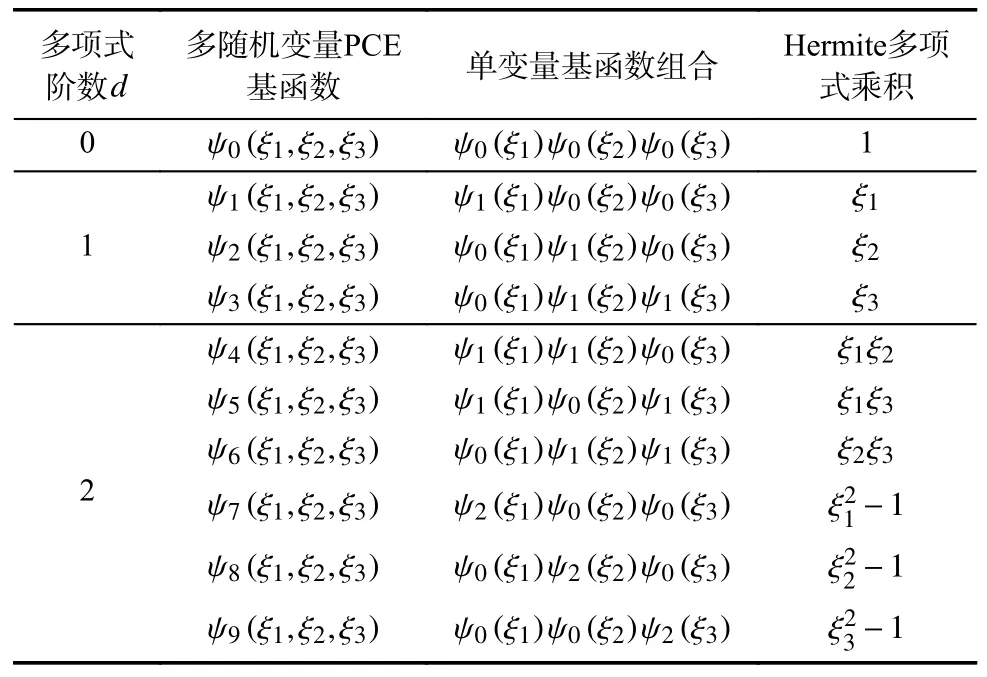
表2 总阶数d=2和3个随机参数的PCE基函数Tab.2 PCE basis function with total order d=2 and three random parameters

1.2 NIPC方法

混沌多项式系数求取是采用多项式展开方法进行不确定性分析的关键，决定着α∗的精度。通常，可通过侵入式法(intrusive method)和非侵入式法(nonintrusive method)两种方法来确定PCE系数[17]。计算PCE系数的过程中，侵入式方法需要对原始模型进行改进和调整，而非侵入式方法则不需要改变原始模型，因此NIPC方法广受关注。为了提高计算效率，本文采用点配置NIPC方法。

点配置NIPC方法首先用方程中的PCE替换随机响应或随机函数，然后在随机空间中选择一组ξ=[ξ1,···,ξn]的样本，最后建立一个有N个方程组成的线性方程组。可通过试验或者数值模拟获取对应的α∗(x,ξ)，由式(1)可得式(3)所示的方程组，再通过最小二乘法求解系数αi。

求出混沌多项式系数αi，就可以直接计算出输出响应的随机概率特性。基于NIPC展开各项系数，即可计算随机函数α∗的统计特性，可得：

随机函数的均值：

标准差：

出于计算量的考虑，目前仍局限于选取其中部分样本进行回归，通常选取概率空间出现频率较大的样本点。由于样本点数目少，可以全部用来估算混沌多项式系数，同时保证不确定性的精度。但是，由于回归法中涉及矩阵求逆等运算，针对高维问题可能较为繁琐耗时。所以要将回归法应用于高维问题，需要预先筛选多项式。

2 混合MC/PCE方法

在许多工业问题中经常遇到多参数不确定性分析的情况，一种MC与PCE的混合算法被应用于多参数不确定性分析。

2.1 基于PCE的混合方法理论

对于随机变量X，其具有精确均值E[X]、精确标准差std[X]、精确方差var[X]、概率密度函数P[ξ]，经过N次迭代，且N足够大，则MC均值可被定义为

将随机变量X的低阶PCE近似为随机函数G(ξ)：

将µ[X-λG]定义为

我们可以通过设置λ的值使得var[X-λG]最小，即：

对应的最小值为

协方差cov(X,G)定义为

混合MC/PCE方法有效地将均值估计量µ[X]转化为两个积分，一个用低阶NIPC求解，另一个用MC模拟求解，具有比传统MC算法更快的收敛速度。方差估计量σ2[X]用相同的方法得到：

2.2 混合MC/PCE方法模型

混合MC/PCE方法模型构建出直接描述多参数不确定性和输出响应不确定性之间的函数关系。该模型的输入由两部分组成：一是由电磁仿真算法模拟为MC提供大量样本点从而获得的均值和标准差；二是由电磁仿真算法模拟为NIPC模型提供输出响应量，从而获得多项式混沌系数进而重构混沌多项式展开表达式并得到NIPC多项式的均值和标准差。具体构建流程如图1所示。

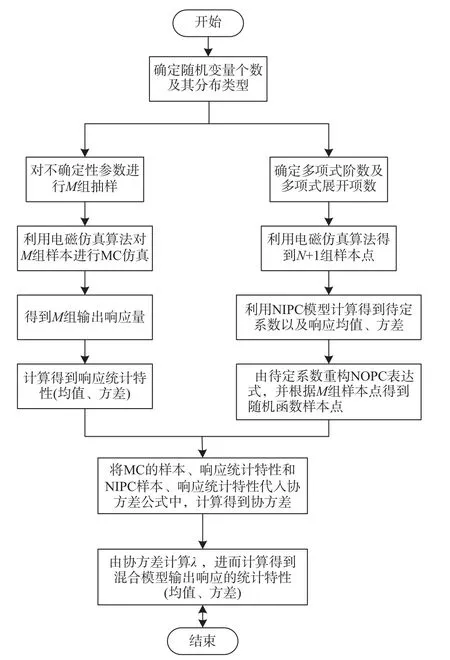
图1 混合MC/PCE方法模型构建流程Fig.1 Hybrid MC/PCE method of model building process

具体实施步骤如下：

1) 确定算例中不确定性参数的分布类型，本次算例中假设随机参数均服从高斯分布，故MC方法的抽样方式采取随机抽样，PCE方法的多项式基函数选择Hermite多项式。

2) 根据算例中不确定性参数的个数N，采用随机抽样方法对各个参数进行M组抽样，本次抽样设置样本点500组。

3) 采用电磁仿真算法对抽样的样本点进行MC仿真试验，得到MC样本以及MC的均值和标准差。

4) 根据算例中不确定性参数的个数N，确定多项式阶数为d=1以及多项式展开项数N+1，对各个参数进行N+1次随机抽样，即输入参数的N+1组样本{ξ(1),ξ(2),···,ξ(N+1)}，并利用电磁仿真算法得到输出响应量α∗的N+1组样本{α∗(1),α∗(2),···,α∗(N+1)}。

5) 对第4步得到的N+1组样本采用NIPC方法对算例进行模拟，利用最小二乘法回归分析构建NIPC模型并计算得到一组PCE系数，由此系数得到NIPC的均值和标准差。

6) 根据NIPC得到的多项式展开系数重构PCE表达式，并将第2步得到的随机抽样的500组样本点带入重构的表达式中得到随机函数G(ξ)样本。

7) 将第3步得到的MC的样本和均值以及第6步得到的NIPC的样本和均值带入式(13)得到协方差cov(X,G)。

8) 根据第7步得到的协方差计算λ。

9) 将MC仿真结果，NIPC样本以及λ的值带入式(9)可以得到µ[X-λG]。

10)利用式(8)可以得到输出响应量的均值。

11)利用式(14)得到输出响应量的标准差，这样就得到了混合MC/PCE模型的统计特性。

所构建的混合MC/PCE方法模型代表的是不确定参数与输出响应均值和标准差之间的函数关系，通过给定不确定性参数均值和标准差，便可通过已构建的混合模型快速计算出输出响应的均值和标准差。

3 仿真结果

算例1平面波斜入射在非均匀等离子体平板上，平面波频率为30 GHz，电磁波入射等离子体平板的入射角度为θ0=30°。仿真模型如图2所示。等离子体区域被平均划分为3层，非均匀各向同性等离子体厚度为d1=d2=d3=50 mm，每层等离子体板的电子密度相互独立且呈高斯分布。本算例采用HMM算法[22]来计算等离子体对平面波的透射系数。每层等离子体均值分别为µ[ne1]=1×1018m-3，µ[ne2]=1×1018m-3，µ[ne3]=1×1018m-3，标准差分别为σ[ne1]=0.05×µ[ne1]， σ[ne2]=0.05×µ[ne2]，σ[ne3]=0.05×µ[ne3]，碰撞频率均为v=1 GHz。

图2 平面波入射3层非均匀等离子体平板仿真模型Fig.2 The simulation model for plane wave propagation in non-uniformly 3-layered plasma

图3给出了电磁波斜入射3层非均匀等离子体平板的透射系数统计特性。可以看到，本文混合MC/PCE方法计算的结果精度和10 000次MC方法可以很好地匹配，尤其是均值计算结果。算例采用一阶NIPC方法和500次MC进行了联合，同时分别将一阶NIPC方法、两阶NIPC方法和500次MC的计算结果与本文方法进行了比较。从图3(b)可以明显看到，混合方法相比于一阶NIPC方法和500次MC有更高的精度，与10 000次MC方法相比，计算量明显减少。两阶NIPC方法比一阶NIPC方法精度更高，这是因为NIPC方法可以通过增加多项式阶数来提高计算精度，但是高阶NIPC方法需要更多的展开项数，增加了算法的复杂度和计算成本。

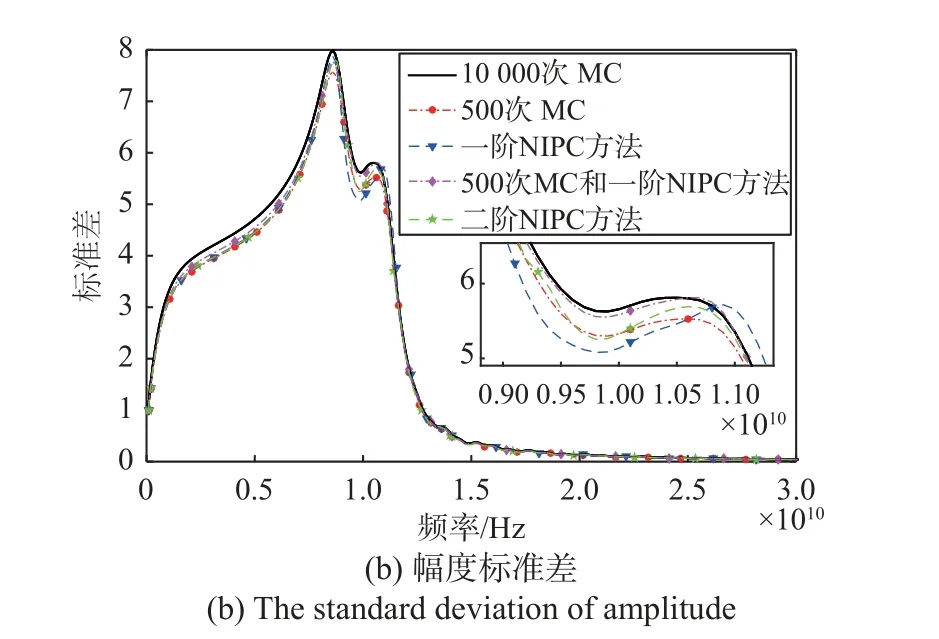
图3 透射系数幅度的均值和标准差（算例1）Fig.3 The mean and standard deviation of transmission coefficient amplitude (sample 1)

算例2平面波斜入射在非均匀等离子体板上，仿真模型如图4所示。模拟区域被划分为10层，非均匀各向同性等离子体厚度均为d=6 mm，每层等离子体板的电子密度独立且呈高斯分布。10层等离子电子密度值如表3所示。标准差均为均值的十分之一，碰撞频率为v=5 GHz。

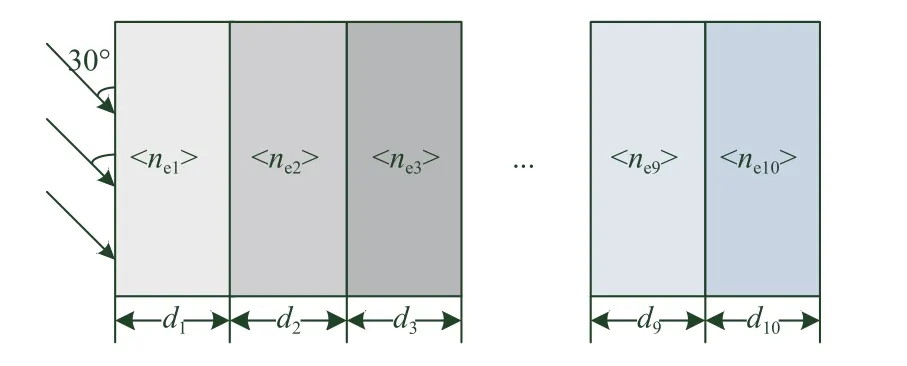
图4 平面波入射10层非均匀等离子体平板仿真模型Fig.4 The simulation model for plane wave propagation in non-uniformly 10-layered plasma

表3 等离子体的电子密度值Tab.3 The electron density value of the plasma

图5分别给出了电磁波通过10层随机等离子体平板透射系数的幅度和相位的统计特性。算例采用一阶NIPC方法和500次MC进行了联合，同时分别将一阶NIPC方法，500次和10 000次MC的计算结果与本文混合MC/NIPC方法进行了比较。可以看出，4种方法得到的透射系数幅度和相位的均值结果较一致；而对于透射系数幅度和相位的标准差来说，相比于一阶NIPC方法和500次的MC，本文中混合MC/PCE方法具有明显的优势，计算结果与10 000次MC方法的结果更加匹配。

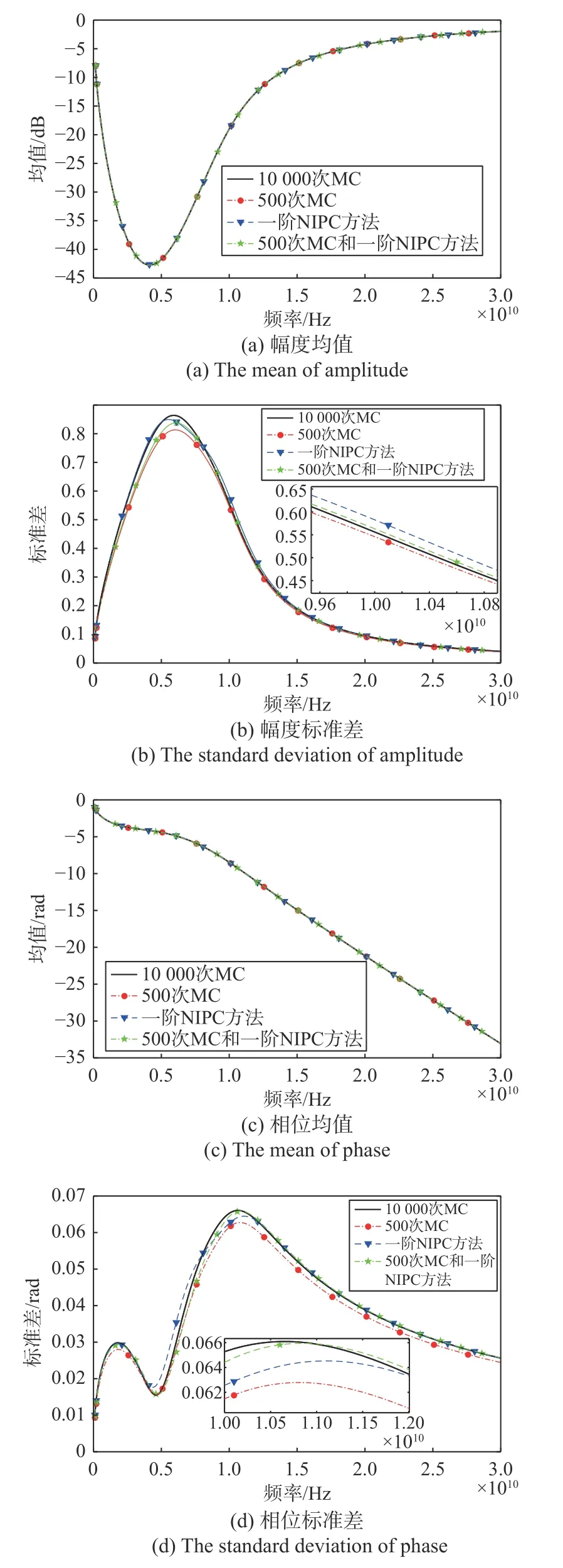
图5 透射系数幅度和相位的均值和标准差（算例2）Fig.5 The mean and standard deviation of the transmission coefficient amplitude and phase (sample 2)

表4给出了该算例中NIPC，MC以及混合方法的模拟次数。可以看出：一阶NIPC方法仿真次数最少只有11次，这是因为只需要计算11个多项式展开系数；500次的MC仿真相对于10 000次MC精度较差；本文所采用的混合方法具有跟10 000次MC方法相比拟的计算结果，但是仿真次数只需要500次，避免了大量的运算。

表4 不同算法仿真次数的比较Tab.4 Comparison of the number of simulations for different algorithms

4 结 论

本文采用一种混合MC/PCE方法，进行了多参数随机等离子体不确定性分析。采用该混合方法进行分层等离子体板多参数电磁散射特性不确定性分析，并将计算结果与MC结果作对比，验证了该算法的正确性，避免了随机变量增多时展开项数随之增多的问题，同时也避免了回归法在高维问题时由于矩阵求逆运算使得多参数不确定性分析出现繁琐耗时的问题。对于本文提出的混合MC/PCE方法，后续还可以将其应用于更复杂的随机等离子体电磁散射特性研究中，如等离子鞘套电磁散射特性。