高速运动等离子体包覆目标的电磁散射特性研究

郭先敏 邓浩川 满良 李海燕 陈伟 杨利霞 薄勇*

（1.计算智能与信号处理教育部重点实验室 安徽大学, 合肥 230601；2.中国航天科工集团有限公司第二研究院, 北京 100854；3.电磁散射重点实验室, 北京 100854）

0 引 言

随着航空航天技术的不断发展和军事科技的快速提升，科学技术中面临的实际电磁问题越来越复杂化。目前，针对临近空间高超声速飞行器的战略需求正在变得十分迫切。临近空间高超声速飞行器具有飞行速度快、巡航时间长和全球快速到达等优点，在军事和民用方面都具有极高的经济价值。当高速飞行器在临近空间执行高机动巡航任务时，会与周围大气产生剧烈摩擦，将飞行器的巨大动能转化为热能，触发飞行器周围空气的电离，从而在飞行器表面形成大量自由运动的带电粒子和中性分子，即等离子体鞘套[1-2]。形成的等离子体鞘套将严重干扰飞行器与雷达之间的无线通信，给高速运动目标的电磁传输、散射和成像等特性带来不可逆转的影响。因此，开展等离子体鞘套包覆下的高速运动目标电磁散射特性理论和实验研究，在航空航天、深空探测，以及雷达技术等领域具有十分重要的意义。

在实际应用中，获取高速目标周围激发的真实流场环境需要耗费巨大的资源和成本，导致高速目标的电磁问题研究变得更加艰难。随着计算机技术的不断提升，电磁数值算法在实际应用中起着越来越重要的作用。其中，时域有限差分 (finite-difference time-domain, FDTD) 方法[3-5]能够处理各种复杂环境下的电磁问题，可以保证很好的精度和有效性，能够有效结合其他方法并应用于更加复杂的电磁计算场景。

近几年，针对高速目标电磁散射特性研究的数值方法在国内外得到了快速的发展。目前，高速运动目标电磁特性的相对论数值模拟方法主要包括两种：基于相对论的移动边界法[6-7]和洛伦兹FDTD(Lorentz-FDTD) 方法[8-12]。Lorentz-FDTD方法自提出以来就得到了广泛关注和快速发展。文献[8-10]利用Lorentz-FDTD方法分析了高速运动目标的回波及电磁散射特性，研究结果表明目标的运动速度会对入射电磁波产生调制，运动目标散射场的频率和幅度与物体速度直接相关。文献[11]通过与散射场多普勒频率解析解的对比验证了三维Lorentz-FDTD方法的有效性。此外，Lorentz-FDTD方法还被应用于具有微动特征的高速运动雷达目标的电磁特性计算[12]以及高速目标的一维距离成像当中[13]。

综上可知，基于Lorentz-FDTD方法的高速目标的电磁特性计算和等离子体与电磁波之间的相互作用研究都在逐步深入，但大部分研究工作主要集中于高速运动普通介质目标的电磁散射问题。然而，基于相对论速度下的包覆等离子体鞘套的高速运动目标的电磁散射特性研究仍然十分缺乏。由于等离子体具有强烈的色散特性，其介电常数与电磁波频率有关，因此必须考虑相对论条件下等离子体介电常数随目标速度的变化。当三维高速运动复杂目标表面包覆等离子体鞘套时，受相对论效应的影响和等离子体的非线性作用，其电磁散射特性必然呈现出更加复杂的变化规律[14-16]。

本文利用相对论原理和Lorentz变换建立了高速运动色散介质的电磁散射模型。基于移位算子(shift operator, SO)-FDTD方法，推导了电磁波在运动色散介质中的电磁迭代方程。在现有研究工作的基础上[17-19]，以高速运动Sears-Haack形状目标为研究对象，并选取高速目标周围流场环境的典型等离子体参数开展仿真实验研究[20-21]，分析了运动等离子体在不同电磁波工作频段时的吸收和散射特性，为研究高速运动等离子体目标的电磁散射机制提供了理论和实验基础。

1 理论推导

基于Lorentz-FDTD方法计算高速运动等离子体包覆目标的电磁特性主要分为以下4个步骤。1) 结合Lorentz变换和FDTD方法建立运动色散介质目标的电磁散射模型；2) 将入射平面电磁波变换到与高速运动目标物保持相对静止的运动坐标系当中；3)在运动坐标系中采用传统FDTD方法求解运动等离子体包覆目标的动态电磁问题；4) 利用逆Lorentz变换将运动坐标系中求得的电磁散射场解的结果进一步转换回与地面(或接收雷达)保持相对静止的实验室坐标系当中。Lorentz-FDTD方法计算运动等离子体目标电磁特性的算法流程如图1所示。

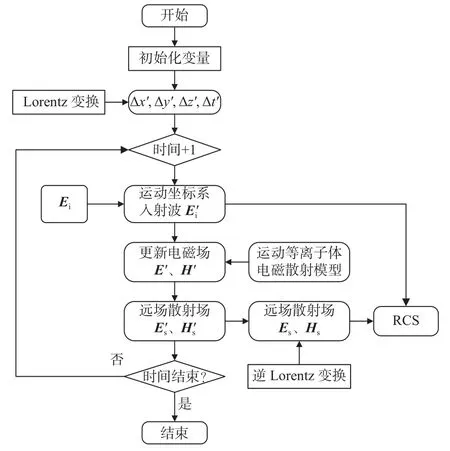
图1 计算运动色散介质电磁特性的Lorentz-FDTD算法流程Fig.1 Flowchart of Lorentz-FDTD algorithm for the calculation of motion EM characteristic

1.1 运动色散介质电磁散射模型

首先，根据相对论原理对运动等离子体目标的电磁参数进行建模。考虑到等离子体的强色散特性，其相对介电常数会随电磁波的频率发生变化。当采用Lorentz-FDTD方法对运动等离子体目标进行建模时，在实验室坐标系下对运动等离子体的电磁建模可以转化为在运动坐标系中对静止等离子体目标进行电磁建模。等离子体的相对介电系数在两个坐标系中具有相同的表达形式，但是值发生了改变。以磁化冷等离子体为例，在运动坐标系中等离子体的相对介电系数εr可以由Drude模型来描述[14,22]：

式中：ωp为等离子体谐振频率；ven为等离子体碰撞频率；ω′为运动坐标系下的电磁波工作角频率。

本文基于SO-FDTD方法求解运动等离子体目标的电磁散射问题，因此等离子体的相对介电常数可以采用有理分数的形式来表示：

式中：ε0为真空中的介电常数；pn和qn分别为等离子体的介电常数的分子和分母系数。

电场的时域本构关系可以表示为[23]

这里，我们定义一个相对论速度变换因子

式中：ki为入射电磁波的单位波矢量；c为真空中的光速。

然后建立实验室坐标系与运动坐标系之间的频域变换关系式：

根据时域和频域之间的转换算子jω′=∂/∂t′，jω=∂/∂t，等离子体的相对介电常数有理分数的频域形式(2)可以进一步在时域表示为

接着将介电常数的时域形式(5)代入电场的时域本构关系(3)中并进行差分离散，可以得到电场的离散时域本构关系为

最后，根据公式(6)，可以得到电场在运动色散介质中的迭代方程为

1.2 引入运动坐标系的入射电磁波

1.2.1 时间和空间的网格转换

假设目标以速度v进行匀速运动，运动坐标系以相同的速度v和高速运动目标保持相对静止，实验室坐标系与地面(雷达)保持相对静止。根据相对论原理，实验室坐标系和运动坐标系之间的空间和时间网格遵循Lorentz变换：

1.2.2 运动坐标系的入射电磁波

在Lorentz-FDTD方法中，由于实验室坐标系与运动坐标系之间存在相对运动，需要根据相对论原理将入射电磁波转换到运动坐标系中进行求解计算。根据电磁波的相位不变原理(式(9))[11]，运动坐标系中电磁波频率ω′i、振幅以及入射平面电磁波波矢量k′i的变换关系如式 (10)~(13)所示。

式中：ωi，E0分别为实验室坐标系中入射电磁波的角频率和振幅；ki0为入射电磁波的波数；为入射电磁波波矢的单位向量；ψ为入射电磁波电场极化方向与速度v之间的夹角；θi为与+z轴的夹角；φi为在xOy平面内的投影与+x轴的夹角。

1.3 运动坐标系的远场散射场

由于运动坐标系与高速运动目标保持相对静止，在运动坐标系中可以采用传统FDTD方法对动态目标的电磁散射问题进行求解计算。目标在运动坐标系中的远场散射电磁场可以由近场数据进行外推得到。首先根据等效原理在FDTD散射场区域内设置一个封闭的虚拟边界作为外推边界，并计算出虚拟边界上的切向电流和切向磁流，然后根据惠更斯原理将该面上的等效电磁流进行外推。运动坐标系中三维远区场公式可以表示为：

式中：η为自由空间中的波阻抗；w′(t)和u′(t)可以通过对公式(16)和(17)进行逆傅里叶变换得到。

式中：r′为r′幅值；r′为观察点的位置矢量；为r′的单位矢量；s为沿r′方向的散射电磁场。

1.4 电磁场的Lorentz变换

由于麦克斯韦方程组满足协变性原理，其旋度方程(18)和(19)在所有惯性系中都具有相同的表示形式：

但是由于实验室坐标系和运动坐标系之间存在着相对运动，电磁场值在两个惯性系中发生了变化，并且两个坐标系中电磁场之间的关系遵循Lorentz变换公式，两个坐标系之间散射电磁场的逆Lorentz变换方程[11]可写为：

在SO-FDTD方法中，电场和磁场作为直角分量形式在时域进行迭代。通过近-远场外推可以得到运动坐标系下的远场散射场E′θ和Eφ′，对其进行空间坐标转换，得到远场散射场在直角坐标系下的各个分量的表示实验室坐标系中远场散射电磁场分量Ex,Ey,Ez通过对运动坐标系中的E′x,Ey′,Ez′进行逆洛伦兹变换得到：

根据式(22)，电磁场的各分量为

将时域入射电磁场Ei(t)进行傅里叶变换，得到其频域值Ei(f)，则三维雷达散射截面（radar cross section, RCS）为

2 算法验证

在仿真中，Lorentz-FDTD时空网格设置为：Δx′=Δy′=Δz′=0.025 m，Δt′=Δx′/2c。金属球半径为1 m，并以速度v=0.01c沿着+y方向运动。入射电磁波选择脉宽τ=40Δt′，时间延迟t0=0.8τ的高斯脉冲平面波源。电磁波入射方向为θi=90°，φi=90°。散射角度为θs=90°，φs=180°。图2给出了采用Lorentz-FDTD方法计算的高速运动金属球的后向RCS与Mie理论解析结果的对比。可以看出：当物体速度v=0时，在电磁波工作频率为0~350 MHz内，Lorentz-FDTD方法计算的金属球的后向RCS结果与Mie理论的解析结果能够很好地符合，两种方法计算得到的RCS之间的最大误差小于2 dB，证明了Lorentz-FDTD方法的有效性。

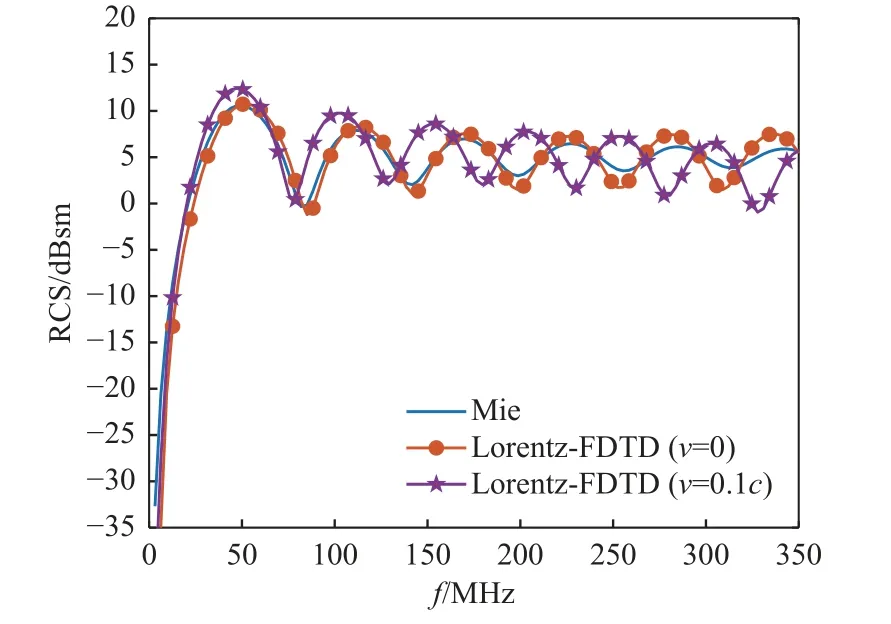
图2 Lorentz-FDTD方法和Mie理论计算的运动金属球的后向RCS对比Fig.2 Comparison of the RCS of a moving metal sphere calculated by Mie theory and the Lorentz-FDTD method

3 计算结果

本文基于Lorentz-FDTD方法研究包覆等离子体鞘套的高速运动Sears-Haack形状目标的电磁散射特性。Sears-Haack形状目标的数学建模方法在文献[24]给出，在xOy平面内的二维投影及尺寸参数见图3。在仿真实验中，三维Lorentz-FDTD中的时间和空间网格设置为：Δx′=Δy′=Δz′=0.002 4 m，Δt′=Δx′/2c。入射平面电磁波采用调制高斯脉冲，调制频率f0=6 GHz，带宽B=4 GHz，脉宽τ=1.7/B，t0=τ。电磁波的入射方向为θi=π/2，φi=π/2；极化角度α=π/2；接收角为θs=π/2，φs=3π/2。调制高斯脉冲信号的数学表达形式为

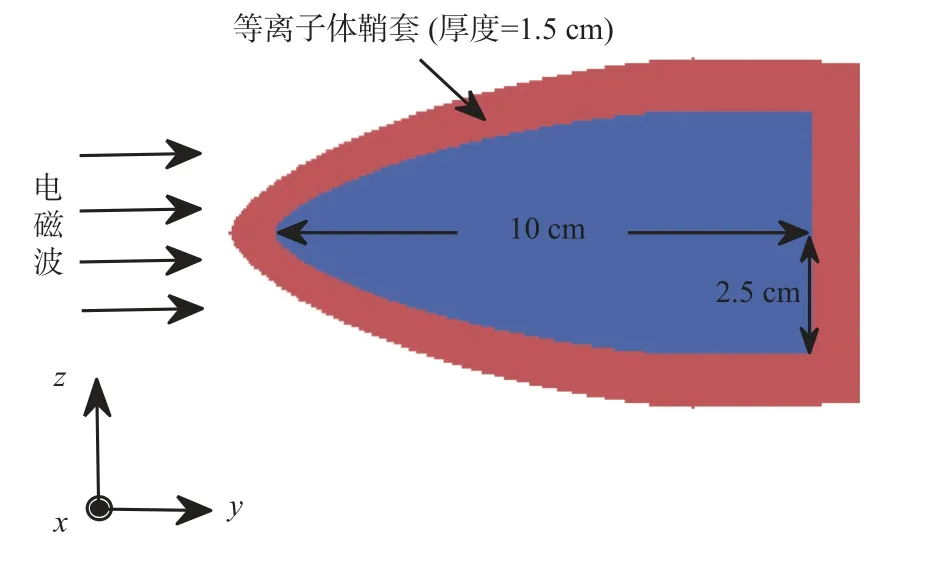
图3 Sear-Haack形状目标模型Fig.3 Model of the Sear-Haack shape target

3.1 高速运动Sears-Haack金属目标电磁散射特性研究

本节分析Sears-Haack形状高速运动金属目标的电磁散射特性，分别在时域和频域分析目标在不同运动速度下的远场散射特性。图4给出了不同物体运动速度大小以及不同运动方向时目标的后向RCS随电磁波频率的变化。可以看出，当目标的运动速度与电磁波的入射方向平行时(沿±y方向)，受相对论效应的影响，运动目标的后向RCS随物体速度大小的变化最为明显。当目标以远离入射电磁波源的速度运动时(沿+y方向)，后向RCS会朝低频端发生频偏(即红移)，在f=6.5 GHz处，目标速度为0.05c和0.1c时，RCS朝低频分别产生约0.3 和0.6 GHz的频偏。当目标靠近入射电磁波源运动时(沿-y方向)，后向RCS朝高频端产生一段频偏(即蓝移)，在f=6.5 GHz处，目标速度为0.05c和0.1c时，RCS朝高频产生约0.3 和0.6 GHz的蓝移。然而当目标以v=0.05c和v=0.1c沿着+x或+z方向运动时，目标后向RCS随电磁波频率的变化与目标静止(v=0) 时完全一致，这是由于背向散射场的多普勒效应仅取决于物体在沿着电磁波入射方向上的速度大小，当物体运动方向垂直于电磁波入射方向时，速度大小的变化不会引起电磁波频率的蓝移或红移。

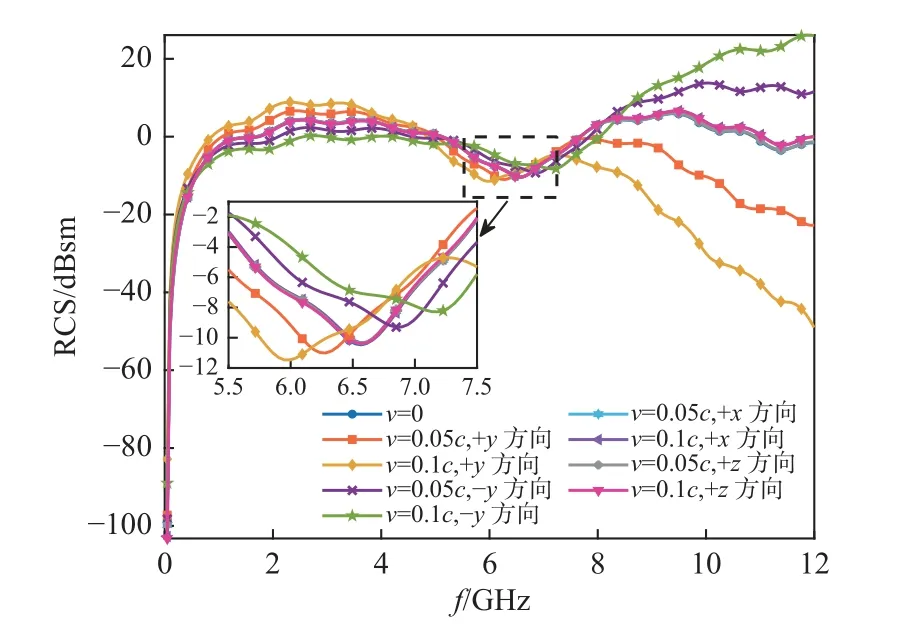
图4 不同运动速度下目标的后向RCSFig.4 Backscattering RCS at different velocities of highspeed moving target

运动目标后向散射场产生的频偏大小与物体速度、电磁波入射方向以及电磁波工作频率密切相关。因此，本节采用频率为f0=1 GHz和6 GHz的时谐场源信号对目标进行探测。当目标以速度15和25 马赫运动时，采用Lorentz-FDTD方法计算的运动目标背向散射场的归一化频谱结果如图5所示。可以看出，当目标以速度v为15和25 马赫远离入射电磁波源运动时，电磁波频率发生红移。当f0=1 GHz时，目标速度v为15和25 马赫产生的多普勒频移分别为34 kHz 和57 kHz；当f0=6 GHz时，目标在速度v=15和25 马赫所产生的多普勒频移分别为0.2 MHz 和0.34 MHz。

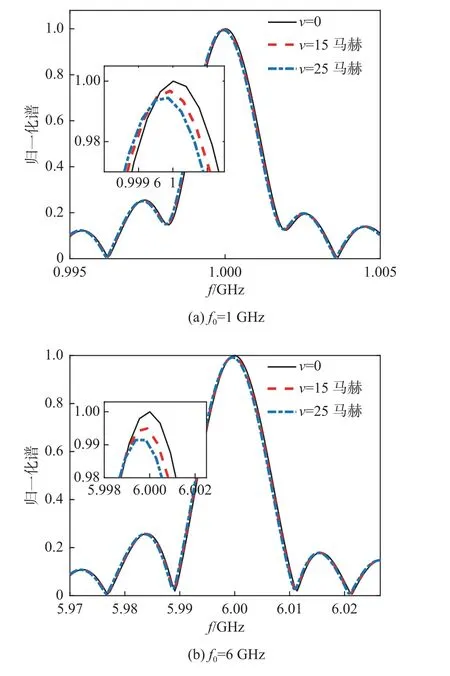
图5 不同调制频率和速度下的高速目标背向散射回波频谱Fig.5 Backscattering echo spectrum of a high-speed target at different velocities and different modulated frequencies

图6为Sears-Haack高速运动目标的时域回波特性。图6(a)为入射电磁场的时域波形，图6(b)~(f)为当目标沿不同方向运动时接收到的高速运动目标后向散射时域回波。对比图6(b)和6(c)可以看出，当目标远离入射电磁波源运动时，后向散射回波信号在时间上产生延迟，散射信号波形在时域上有所展宽，并且幅值略有减小；对比图6(b)和6(d)可以看出，当目标靠近入射电磁波源运动时，后向散射场回波幅值会增大，散射回波信号波形在时间轴上被压缩，并且雷达将提前接收到来自运动目标的回波信号；对比图6(b)、(e)和(f)可以看出，当目标垂直于电磁波入射方向运动时，目标的后向时域回波与目标静止时接收到的回波信号较为接近，再次证明了当物体运动速度与入射电磁波方向垂直时，速度的变化对目标散射场的影响十分微弱。

图6 不同运动方向下目标后向散射场的时域波形Fig.6 Time-domain waveforms of backscattering field of high-speed target for different motion directions

图7(a)和(b)给出了当运动目标速度分别为0.05c和0.1c时，不同物体运动方向φv后向散射场在调制频率f=f0处产生的多普勒频移[13]。可以看出，当物体运动速度与电磁波入射方向平行时，即θv=90°和φv=270°时，后向散射场产生的多普勒频移(红移和蓝移)最大；而当运动方向与电磁波入射方向垂直时，即θv=0°和φv=180°时，在两个运动速度下的散射场的多普勒频移均为零。

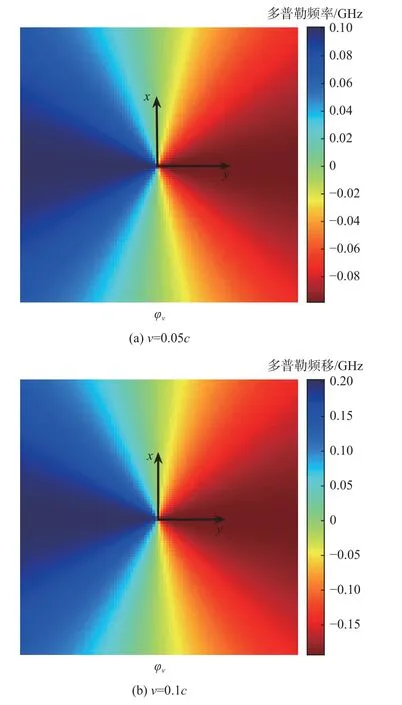
图7 不同运动方向下后向散射场的多普勒频移Fig.7 Doppler shift of the backscattering field at different directions of motion

3.2 包覆等离子体鞘套的高速运动目标电磁散射特性分析

针对高速运动目标表面包覆均匀分布等离子体鞘套的情况，本节进一步研究等离子体电子密度ne、碰撞频率ven、涂敷厚度d对高速运动Sears-Haack目标电磁散射特性的影响。由文献[6]可知，当高超声速飞行器以15马赫的速度在30 km处高速飞行时，等离子体的平均电子密度变化范围为3×1012~9×1018m-3，碰撞频率为8×107~4.5×1010Hz。在仿真实验中，Lorentz-FDTD的时空网格设置为Δx′=Δy′=Δz′=0.001 6 m，Δt′= Δx′/2c。入射信号源采用高斯调制脉冲，其中心频率f0=6 GHz，带宽B=4 GHz。电磁波入射角度为θi=π/2，φi=π/2。目标以速度v=0.05c沿着θv=π/2，φv=3π/2方向运动。等离子体的相关电磁特征参数在表1中给出。

表1 等离子体鞘套参数设置Tab.1 Parameters of plasma sheath

图8为当目标以v=0.05c朝着入射电磁波源运动时，目标后向RCS随等离子体电子密度的变化。可以看出，在不同的电磁波工作频率下，等离子体鞘套对运动目标后向RCS的影响不同。当电磁波工作频率较低(f<2 GHz)时，等离子体鞘套对电磁波的反射会增强，由于受到物体形状以及等离子体介电常数的影响，在低频段内，由于电磁波一部分沿着目标表面进行传播，对目标远场散射场造成影响，导致远场散射RCS随电磁密度的升高而增大。当电磁波工作频率f为2~8 GHz时，随着电子密度从3×1016m-3增加到2×1018m-3， RCS呈现先减小后增大的变化趋势；当ne=5×1017m-3时，目标的后向RCS衰减最大，与无等离子体情况时相比RCS平均降低约20 dB；而当ne=2×1018m-3时，RCS平均降低约11 dB。这主要是由于当电子密度ne=5×1017m-3时，等离子体频率与电磁波中心频率最为接近，因此加强了等离子体对电磁波的共振吸收，造成入射电磁波能量的衰减，从而导致运动目标的后向RCS在电子密度ne=5×1017m-3时衰减最大。当电磁波工作频率f为8~12 GHz时，与无等离子体情况相比，ne=1×1018m-3时后向RCS平均降低约23.7 dB，ne=2×1018m-3时RCS平均降低约17.3 dB。而当电子密度小于8×1016m-3时，等离子体对RCS衰减较小。这是由于较低的电子密度对高频段电磁波的吸收较小，而较大的电子密度会增强等离子体对电磁波的反射。因此随着电子密度的升高，RCS呈现先降低后增大的变化趋势。

图8 不同电子密度下高速运动目标的后向RCS (v=0.05c)Fig.8 Backscattering RCS of high-speed moving target with different plasma electron densities (v=0.05c)

图9为目标以v=0.05c朝入射电磁波源运动时，目标的后向RCS随碰撞频率ven的变化。可以看出，等离子体碰撞频率对目标后向RCS的影响与电子密度的取值相关，当ne=1×1017m-3，电磁波工作频率f<2 GHz时，RCS随碰撞频率的增大而减小。由图8可知，f<2 GHz时，电子密度的增加会导致目标后向RCS的增大，当电子密度一定时，随着碰撞频率的增大，等离子体对表面电磁波能量的消耗增加，削弱表面电磁波对目标远场散射场的影响，因此目标的后向RCS随着碰撞频率的增大而逐渐降低。f为2~6GHz时，碰撞频率从2 GHz增加到40 GHz时，RCS呈现出先减小后增加的趋势。这是由于当电磁波工作频率接近等离子体频率时，等离子体对电磁波的吸收效应会随着碰撞频率的增加而增加。而当碰撞频率增大到一定程度 (ven=20 GHz) 时，后向RCS不再随碰撞频率的增大而减小。这是由于当碰撞频率远大于电磁波工作频率时，电磁波能量来不及被等离子体中的电子吸收又再次发生碰撞，导致等离子体对电磁波的吸收效应减弱，因此后向RCS在ven>20 GHz时反而增加。

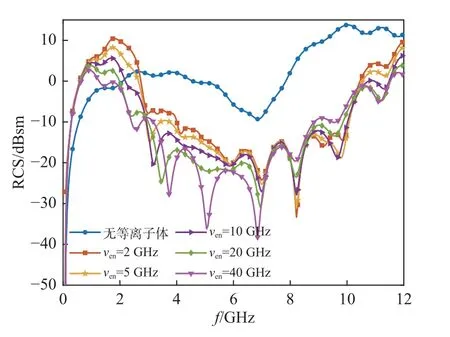
图9 不同碰撞频率下高速运动目标的后向RCS (v=0.05c)Fig.9 Backscattering RCS of high-speed moving target with different plasma collision frequencies (v=0.05c)

图10为当目标以v=0.05c朝着入射电磁波源运动时，目标的后向RCS在不同等离子体鞘层厚度时的变化。可以看出，覆盖等离子体可以在一定程度上降低运动目标的后向RCS。当电磁波工作频率f为0~2 GHz时，运动目标后向RCS随等离子体鞘套厚度的增加而增大，这是由于等离子体鞘套厚度的增加增大了运动目标的特征尺寸，因此后向RCS在低频段内会略微增大。当电磁波工作频率f为2~8 GHz时，运动目标后向RCS会随等离子体厚度的增加而减小。这是由于随着厚度的增加，等离子体对电磁波吸收的作用距离增加，在电磁波工作频率远大于等离子体频率情况下，当等离子体涂敷厚度增大到一定程度时(如d=2.0 cm)，运动目标的后向RCS不再随着厚度的增加而减小。

图10 不同等离子体厚度下高速运动目标的后向RCS(v=0.05c)Fig.10 Backscattering RCS of high-speed moving target at different thicknesses of plasma sheath (v=0.05c)

3.3 涂敷等离子体目标与运动金属目标对比

为了对比包覆等离子体鞘套的高速运动目标与普通运动金属目标的电磁散射特性，本节采用Lorentz-FDTD方法计算不同运动速度时的目标后向RCS，并分析电磁波在运动等离子体中的反射特性。仿真实验中入射电磁波和网格设置均与3.2节相同，ven=20 GHz，d=1.5 cm，目标沿着电磁波入射方向运动时有v>0(θv=π/2，φv=π/2)，目标与电磁波入射方向相反时有v<0(θv=π/2，φv=3π/2)。

图11为当ne=1×1017m-3、5×1017m-3和2×1018m-3时，电磁波通过不同运动速度等离子体时的反射系数[25]随电磁波频率的变化。可以看出，等离子体对电磁波的反射随电子密度的增加而增大。当等离子体处于不同的速度时，由于相对论效应的影响，等离子体对电磁波的反射系数会发生不同程度的偏移。当目标远离电磁波运动时 (v>0)，反射系数会朝低频发生偏移。从图11还可以看出，反射系数随着速度的增大略有减小。当目标靠近电磁波运动时(v<0)，反射系数会朝高频移动，并且随着速度的增大反射系数略微增大。

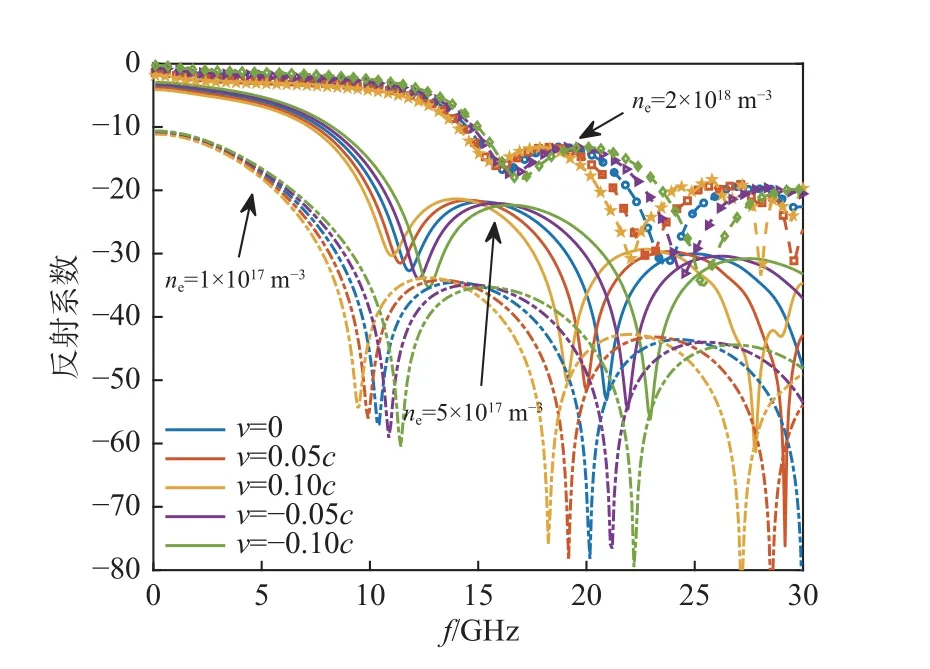
图11 不同电子密度下电磁波透过不同速度等离子体的反射系数Fig.11 Reflection coefficients of EM waves through plasma with different velocities for different electron densities

图12为当目标以速度v=0、0.05c、0.1c沿θv=π/2,φv=3π/2方向运动时，涂敷不同电子密度等离子体与无等离子体涂敷时的高速运动目标后向RCS对比。可以看出，在不同等离子体电子密度下，运动目标的后向RCS在不同电磁波频段的衰减不同，这是由于电子密度的变化会改变等离子体频率，导致等离子体对电磁波的共振吸收范围发生变化。当ne=1×1017m-3时等离子体对低电磁波频段的吸收效应较大，而当ne= 2×1018m-3时等离子体对高频电磁波吸收效应增强，因此在ne=1×1017m-3时后向RCS在低频段显著降低，ne=2×1018m-3时后向RCS在高频波段衰减较大。当运动目标表面无等离子体涂敷时，随着物体运动速度的增大，后向RCS曲线会朝高频端产生偏移，并且在高电磁波频段处RCS明显增加。这是由于目标靠近入射电场波源的运动引起电场波频率蓝移，削弱了等离子体对电磁波的吸收效应，因此在高频段RCS会随速度的增大而增加。

图12 不同电子密度和速度下涂敷等离子体与无涂敷等离子体时高速运动目标的后向RCS对比Fig.12 Backscattering RCS at different velocities for different electron densities with or without coated with plasma

图13为ne= 5×1017m-3时不同速度下的Sears-Haack目标与金属目标后向RCS对比。可以看出，f>2 GHz时运动目标的后向RCS显著降低。这是由于当ne=5×1017m-3时，等离子体频率与入射电磁波调制频率接近，加强了等离子体对电磁波共振吸收效应，导致入射电磁波能量的最大衰减。

图13 不同速度下Sears-Haack目标与金属目标的后向RCS对比Fig.13 Backscattering RCS comparison for Sears-Haack target and metal target at different velocities

4 结 论

本文基于相对论原理对高速运动色散介质目标的电磁特征参数进行了物理建模，基于三维运动等离子体的电磁散射模型，利用Lorentz-FDTD方法推导了运动色散介质的电磁场迭代方程式。并采用该方法研究了包覆等离子体鞘套下高速目标与电磁波之间的相互作用，通过选取等离子体流场的典型特征参数，分析相关电磁特征参数的变化对目标远场特性的影响，得到以下结论：

1) 运动等离子体的介电常数不仅与电子密度、碰撞频率和电磁波频率密切相关，同时还取决于物体的运动速度。

2) 运动目标的远场散射特性与目标形状、物体速度及等离子体特性参数有关。

3) 运动等离子体对电磁波的吸收和散射机制变化较为复杂。当目标靠近电磁波源运动时，由于多普勒效应使电磁波频率发生蓝移；当电子密度一定时，随着目标速度的增大等离子体对低频段电磁波的吸收加强，而对高频段电磁波的散射能力加强。

本文的研究结果能为包覆等离子体鞘套的高速运动目标的电磁散射特性研究提供理论和实验基础。考虑到在许多实际环境中，等离子体鞘套在空间上总是呈现多种非均匀分布状态并会受到各种时变规律的调制，因此，下一步考虑将Lorentz-FDTD方法应用于分析时空非均匀分布的运动等离子体鞘套与电磁波之间的相互作用研究中。