一种采用B样条插值的改进能量算子在电梯电机轴承故障诊断中的应用

孙 敏，魏 禹，马吉祥，周 璇

(1.西安交通工程学院 机械与电气工程学院，西安 710300；2.西安邮电大学 自动化学院，西安 710121)

0 引言

电梯系统在公共交通和商业设施中扮演着至关重要的角色。其中，电机是维持电梯运行不可或缺的核心组成部分。电梯电机通过将电能转换为机械能来驱动电梯的运行。当启动时，电机带动轿厢旋转，并借助钢缆提升货物或乘客。当到达指定楼层时，停止电机转动使得电梯停止运行。此外，电梯电机还通过控制系统来控制电梯的速度和方向，确保电梯稳定运行。电梯电机需要定期检查和维护，以确保其正常运行及附件的稳健性。若出现故障或失灵，将影响电梯系统的正常运转，不仅危及使用者安全，也会给操作、维修和维护带来无谓困扰。因此，对于保养和维护电梯电机来说，其重要性不言而喻[1-2]。

轴承作为电梯电机的重要传动件起到了重要的传递作用，但由于其工作环境较为恶劣导致容易损坏，因此对轴承的早期故障检测非常重要。主轴传动轴承的好坏对于主要的回转精度、刚度、热特性和动态性都有着较大的影响[3-4]。此外，轴承有助于通过减少运动部件之间的摩擦来降低机械能量损失和需求进行维护。摩擦是由两个物体之间的物理接触引起的，在电机中，许多运动部件相互摩擦导致发热。这种热量会使轴承和其他部件升温，可能导致电机或其他部件损坏。为了减少摩擦，电机必须使用轴承。轴承帮助通过在运动部件之间减少因摩擦产生的多余热量和能量损失来延长电机的使用寿命。因此，对于电梯电机中轴承的状态监测与故障诊断是保证电梯系统正常运转的重要环节。当轴承内圈或外圈出现缺陷时，当滚珠通过该缺陷时，就会产生表示轴承故障特征的周期性脉冲。当能量被内部阻尼耗尽后，这些脉冲就会以近似于指数包络线的方式衰减。这种信号被认为是调制信号，其中调制信号的基频(包络)就是轴承的故障特征[5-6]。因此，振幅解调产生的包络信号传达了更多的故障信息，这是原始信号的傅立叶频谱分析无法获得的。可以说，解调技术是为这些调制信号量身定制的处理方法。

近年来，一种流行的解调方法，非线性能量算子技术得到了广泛应用。该种解调方法可以从原始信号中捕获调幅-调频信号。在这些非线性能量算子工具中，最具代表性的是Kaiser[7]设计的Teager能量算子(TEO，teager energy operator)。该算法是一种非线性微分算子，能够有效地估计任意调制信号的时变包络。此外，与其他常用解调分析工具相比，如高频共振解调方法(HFR，high frequency resonance)和希尔伯特变换解调方法(HT，hilbert transform)，它具有以下特点[8-9]：1) 由于TEO可以提供一个小的时间窗，使其成为调制信号局部分析的理想工具，同时具有优越的定位特性；2) TEO只对3个相邻的信号样本进行操作，实现非常简单，占用计算机资源少，计算量少；3) 它是一种无参数方法，从而减轻了参数选择和重新校准的步骤。基于这些优点，TEO已广泛应用于机械故障诊断。文献[6]针对强背景噪声下滚动轴承振动信号故障特征信息难以提取的问题，提出了结合固有时间尺度分解形态滤波和TEO相结合的轴承故障特征提取方法。文献[10]针对轴承故障信号中微弱周期性冲击的特征提取问题，提出参数优化集合经验模式分解与TEO结合的轴承故障诊断方法。文献[11]针对轴承故障信号中伴有轴转频率和噪声等问题，提出了基于信号共振稀疏分解与TEO结合的轴承故障诊断方法。文献[12]针对轴承故障的特征提取和识别问题，提出了一种基于小波各子带Teager能量熵和模糊c均值的故障诊断方法。文献[13]提出了一种利用TEO对定子电流进行频谱分析的解调新方法。文献[14]提出将轴承振动信号转换到Teager能量域，并采用统计和基于能量的度量对其进行特征化，从而起到故障特征提取的作用。

然而，TEO方法容易受到噪声的影响，尤其是在背景噪声比较强烈的情况下，TEO一般是无法直接从这种噪声干扰信号中提取有用的故障信息的。电梯运行环境嘈杂，其动力主要由曳引机提供。因此，在电梯运行过程中必然会产生噪声，尤其是机械动作所致。当曳引机产生动力后，它通过蜗杆传动减速箱和齿轮传递曳引机所产生的力。在传输过程中，齿轮之间的相互作用可能导致噪音问题的出现。因此从电梯电机故障轴承中提取的振动信号中可能包含了强烈的背景噪声。将TEO直接应用于电梯电机故障信号是无法提取故障特征频率。因此，需要对原始信号进行前处理处理后，才能有效提取轴承故障特征，一般的处理思路是将TEO与不同的滤波方法进行结合，先使用前滤波方法对原始故障信号进行处理，然后将TEO作用于滤波后的信号，这就降低TEO对噪声的敏感度，从而提取出了轴承故障特征频率。虽然这种联合的方法有效，但是这种联合的方法有一个明显的不足，就是增加了故障特征提取的步骤，这样不仅加大了应用的复杂性，同时也加重了算法运行负荷，造成运行耗时过长的问题，这就导致这种方法在实际使用中的局限性。为了克服这个不足，本文采用了一种新颖的基于B样条插值的能量解调方法[15]。在这个方法中，首先采用B样条理论设计样条插值多项式，这种插值多项式一定程度上起到了时变滤波器的作用。但这和之前的所说的联合方法中真正的滤波器不同，因为它的原理更加简单，同时它是嵌入TEO之中，没有繁琐的滤波步骤，从而使用该方法更加直接，也降低了计算复杂度。该种融合B样条插值的TEO能量解调方法可以增强其本身的鲁棒性，从而更好地应对强背景噪声的影响。将该方法应用于真实电机轴承故障信号中取得很好的效果，验证了该方法的实用性。

1 基于B样条插值的Teager能量算子

很多文献对于B样条插值的构建都进行了相关研究，本文中采用文献[16-17]中的方法进行构建。B样条插值技术是以较低的速率对信号进行重采样，并采用抗混叠滤波器实现最小误差的信号逼近。该方法不仅是一种数据压缩方法，而且是一种噪声抑制策略。用满足特定连续性约束的分段多项式来表示这些函数。假设给定一个初始信号x(n)，该信号在B样条空间可以表示为：

(1)

式中，βn(t)表示n阶B样条函数；c(i)为B样条的系数；m代表节点之间的步长。从式(1)中可以看到，最终的近似输出是由阶数n、结点步长m和系数c控制的，这意味着B样条近似是这些系数给定的情况下，确定使最小二乘误差准则最小化。最小二乘误差准则定义为：

(2)

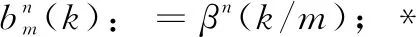
c(i)的解可以用下式表示：

(3)

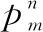
接下来，讨论如何构建B样条插值的节点。如上所述，B样条插值函数是分段多项式。期望的信号是由这些多项式片段连接在一起形成的，这些连接点称为节点。因此，节点是B样条插值重要组成部分。对于一组多成分信号，可以使用下面的信号模型进行表示，

(4)

式中，am(t)>0为幅值；φm(t)代表相位。

通过式(4)，可以得到瞬时幅值和瞬时频率：

(5)

(6)

由于一个多成分信号都可以由两个信号的组合来进行表示，即：

z(t)=A(t)ejφ(t)=a1(t)ejφ1(t)+a2(t)ejφ2(t)

(7)

因此式(5)和(6)变为：

(8)

φ′(t)=

(9)

令cos[φ1(tmin)-φ2(tmin)]=-1，显然这时A(t)为局部最小值。将其代入(8)和(9)得到：

|a1(tmin)-a2(tmin)|=A(tmin)

(10)

(11)

又因为A(tmin)为局部最小值，所以A′(tmin)=0。因此可得：

(12)

同理，当在tmax时，A(tmax)为局部最大值，令cos[φ1(tmax)-φ2(tmax)]=1，则得到：

(13)

a1(tmax)+a2(tmax)=A(tmax)

(14)

(15)

通过解式(8)到(12)，可得到a1(tmin)，a2(tmin)，φ1(tmin)和φ2(tmin)。同样地，通过式(13)到(15)，可得到a1(tmax)，a2(tmax)，φ1(tmax)和φ2(tmax)。则a1(t)可通过一组内插点{a1(tmin)，a1(tmax)}得出。a2(t)，φ1(t)和φ2(t)也可以通过同样的方式得出。通过得出的a1(t)，a2(t)，φ1(t)和φ2(t)则有：

(16)

式中，η1(t)和η2(t)由一组内部插值点φ′({tmin})A2({tmin})和φ′({tmax})A2({tmax})得出。

则节点可通过下式得出：

(17)

通过以上B样条理论构建的B样条插值，可以对采样离散信号进行插值操作并得到一组插值信号如下，

(18)

显然，sv(t)是原始离散信号x[n]在连续时间域上的扩展。基于B样条插值的能量解调算法的基本思想就是将连续时间域的信号sv(t)应用到TEO方法的表达式中，即：

(19)

其中：

至此，整个方法可称为基于B样条插值的能量解调方法。

2 模拟信号仿真

为了验证本文所提出的基于B样条插值的TEO方法的实用性，此部分采用一个故障轴承模型用以模型轴承故障信号，该轴承故障模型如下所示[18]：

(20)

式中，Am代表冲击振幅；ξ代表阻尼系数；ωn代表系统共振频率；T代表故障周期；τi为第i次冲击相对于T的微小波动；u(t)是单位阶跃函数；n(t)代表模拟的高斯白噪声。信号采样点数为20 000，采样频率为20 kHz。故障特征频率为FCF=100 Hz。

为了更好地体现所提方法的实用性和优越性，加入强背景噪声，使轴承故障信号的信号比SNR=-10 dB。本文所提方法应用于该模拟信号的过程：首先将基于B样条插值的TEO应用于模拟信号从而得到时域包络信号，然后利用傅里叶变换将时域包络信号从时域转换为频域，得到包络信号的能量谱图从而在得到故障特征频率。

图1为加入强背景噪声的模拟轴承故障信号时域图。从图中可以看到，轴承故障脉冲序列已经被强烈的背景噪声淹没，无法分辨。首先使用前文提到的经典解调方法，即Teager能量解调方法(TEO)和希尔伯特变换解调方法(HT)，对该轴承模拟故障信号进行变换，其变换后信号的包络谱如图2(a)和(b)所示。从TEO和HT的包络谱中可以发现，常用的经典解调方法TEO和HT都未能从强噪声污染的信号中分离出故障特征频率。正如前文中所述，这是由于HT和TEO对噪声较为敏感，尤其是强背景噪声的工况下。

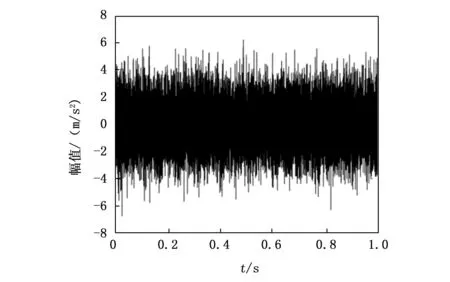
图1 模拟轴承故障信号

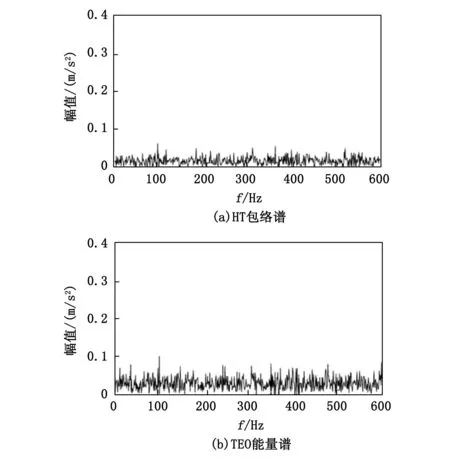
图2 HT和TEO方法提取结果

现使用本文提出的基于B样条插值的TEO方法对其进行故障特征频率的提取，提取结果如图3所示。从图中可以清楚地看到，本文所提方法可以较好地提取出模拟轴承故障特征频率100 Hz和它的2倍频、3倍频和4倍频。这是因为B样条插值可以起到一个时变滤波的作用，经过B样条插值后的信号可以降低对TEO的影响，从而更好地提取故障特征。

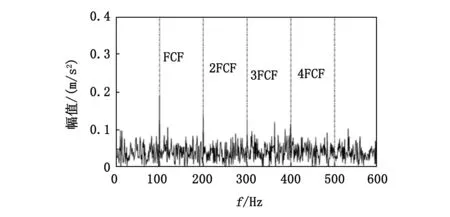
图3 基于B样条TEO得到的能量谱

通过该模拟信号验证，可以看到经典的TEO和HT解调方法虽然有很多优点，如运算速度快和无参数设置等，但是它们对噪声尤其是强背景噪声十分敏感。因此，将其应用在原始的轴承故障信号中很可能无法直接提取出故障特征频率。而通过B样条插值改进的TEO可以很好地提取出故障特征频率。

为了更加全面地体现B样条的时变滤波作用，在不同信噪比条件(-10 dB到10 dB)下进行对比分析。图4为不同的信噪比条件下的输出信噪比的变化曲线图。从图中可以看到，通过所提方法处理后的输出信号的SNR值都要比原始信号的SNR值要高，说明所提出的B样条插值起到很好的滤波效果。

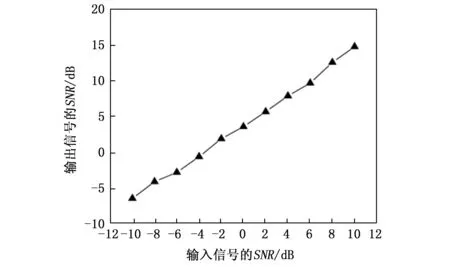
图4 不同信噪比条件下的输出信号的SNR

3 轴承故障特征提取实验

为了进一步验证所提方法的工程实用性，本小节将采用一组真实轴承故障数据来进行验证。本次故障类型分为轴承的内圈故障和外圈故障。并且为了体现所提方法的优越性，在内外圈故障诊断当中还加入了模态分解方法和最小最优熵反褶积的方法进行对比。

本次真实案例所采用的电机轴承故障数据由科廷大学机械工程系提供。该实验数据来自于SpectrQuest机械故障模拟器测试平台。该SpectrQuest实验平台主要由6个模块组成：电动机、转速表、变速控制器、联轴器、正常轴承和故障轴承，如图5所示。

图5 实验平台

该电机故障仿真系统由一台1 hp电机驱动。转速由变速控制器控制，转速范围从0到6 000转/分。轴承座内安装两个MB ER-16 K滚动轴承。左侧安装正常滚动轴承，右侧安装故障滚动轴承进行实验。采用一个联轴器来抑制电机产生的高频振动。振动信号以51 200个/s进行采样。旋转轴以旋转频率29 Hz (1 740 RPM)的速度旋转。表格1为故障轴承的几何尺寸。

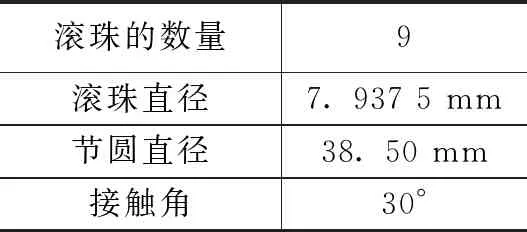
表1 故障轴承的几何尺寸

根据故障轴承的几何信息，计算得到轴承的外圈故障特征频率(BPFO，ball pass frequency outer)为103.59 Hz，内圈故障特征频率(BPFI，ball pass frequency inner)为157.41 Hz。

3.1 内圈故障特征频率提取

首先，进行轴承内圈故障特征频率的提取。图6(a)和(b)为轴承内圈故障信号的时域图和相对应的TEO能量谱。从图6(a)的时域信号中可以看到，微弱的内圈故障脉冲序列已经被噪声掩盖而无法辨认。同时从图6(b)中的能量谱中发现，由于强噪声的存在，TEO无法从该故障信号中提取出内圈故障特征频率及其倍频。

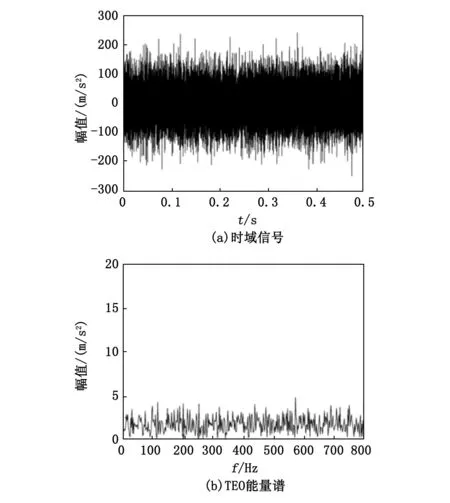
图6 内圈故障信号及其TEO能量谱

现使用本文所提的基于B样条插值的TEO能量解调方法对该信号进行处理，得到的相对应的能量谱如图7所示。从能量谱中可以看到，本文所采用的基于B样条插值的TEO可以从强背景噪声污染的内圈故障信号中提取出内圈故障特征频率157. 41 Hz及其它的前3个倍频，验证了该方法的工程实用性。

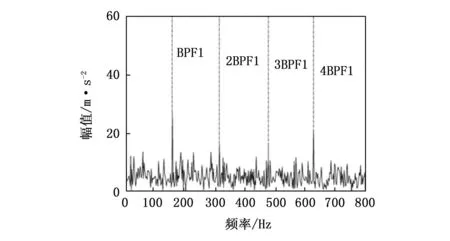
图7 所提方法的能量谱

为了体现该方法的优越性，采用故障诊断中常用的基于模态分解的方法进行对比。这里采用文献[20]中集成经验模态分解(EEMD，ensemble empiricalmode decomposition)和TEO的联合方法。该联合方法的原理是首先使用EEMD方法将轴承故障信号分解成一些列本征模函数(IMF，intrinsic mode function)，在分解的过程中同时达到了过滤噪声的目的，然后选择合适的IMF，最后利用TEO对该IMF进行处理，得到相对应的能量谱，从而达到故障特征提取的目的。

图8为EEMD分解出的IMF，可以看到该EEMD把该原始内圈故障信号分解出了IMF。因此，必须从这5个IMF中挑选出蕴含故障信息最多的一个IMF。这里采用最常用的峭度(Kurtosis)指标来选出合适的IMF从而进行下一步分析。从图8中可以看到，IMF3的峭度值为4.122 1，为5个分解出的IMF的峭度值最大，因此选择IMF3进行进一步分析。最后使用TEO对IMF3进行转换，最终得到的TEO能量谱如图9所示。从能量谱中可以看出，虽然该种EEMD+TEO的联合方法可以提取出故障特征频率，但相比于图6结果，它的故障频率的幅值较低，较难分辨，并且从能量谱中也无法分辨出故障特征频率的倍频。

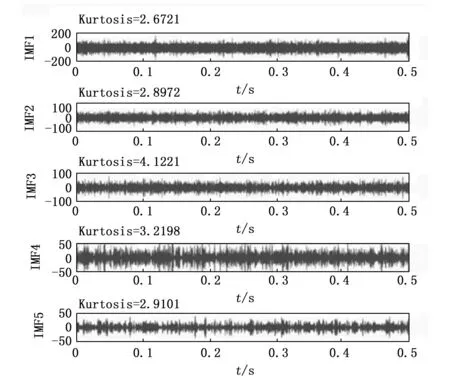
图8 分解的IMFs

图9 IMF3的TEO能量谱

此外，这种联合提取故障特征频率的方法的步骤也较为繁杂，首先使用EEMD分解原始故障信号；然后需选择合适的IMF；最后对合适的IMF进行故障特征提取。而本文所采用的方法更加的简单与直接，因此实用性更强。

3.2 外圈故障特征频率提取

现进行轴承外圈故障特征频率的提取。图10为外圈故障特征信号时域图波形。从图中可以看到，同内圈故障信号一样，外圈故障脉冲序列由于强噪声影响已经无法进行分辨。直接采用TEO或者HT方法进行故障解调是不可行的。

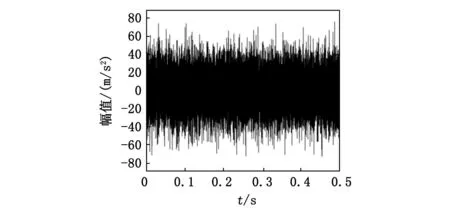
图10 外圈故障信号

现使用本文所采用的基于B样条插值的TEO方法对该外圈故障信号进行故障特征频率的提取，最终提取结果如图11所示。从能量谱可以发现，同内圈故障诊断一样，该方法仍然可以从强背景噪声中提取出外圈故障特征频率及其它的前4个倍频。

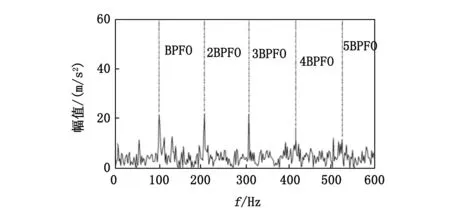
图11 能量谱

类似地，在外圈故障特征提取中，采用文献[21]中一种先进的基于反卷积的方法，即多点最优最小熵反卷积(MOMEDA，multipoint optimal minimum entropy deconvolution adjusted)和TEO方法的与该方法进行比较。MOMEDA方法与EEMD方法相比，MOMEDA既能去除噪声，又能突出故障循环脉冲。此外，基于MOMEDA的故障检测方法不需要选择敏感的IMF，提供了更好的便捷性。但需注意的是，MOMEDA方法中必须事先设置过滤器长度L，这是一个重要的参数。本次对比实验中参数设置为L=2 500。

图12为MOMEDA滤波后的外圈故障波形图。从波形可以看到，与EEMD分解后的IMF不同，MOMEDA不仅去除了大量的背景噪声，还突出了故障脉冲序列。

然后使用TEO对滤波后的信号进行转换。其转换信号的能量谱如图13所示。通过该图可以看到，经过滤波后，TEO也可以很好地从滤波信号中提取出外圈故障特征频率及其倍频。显然基于MOMEDA的方法要明显强于基于EEMD的方法，最主要的原因就是前面所述的MOMEDA可以很好地突出故障脉冲序列。这种方法的提取效果几乎与本文所采用方法的提取效果相似。但值得一提的是，该种MOMEDA方法相对于本文所提方法，虽然它的提取效果相似，但正如前所述，MOMEDA在使用前必须设置滤波器长度，滤波器长度的选择在很大程度上影响着MOMEDA的滤波性能，但是一般滤波器的长度选择都是盲目的或者需要人工经验进行选择。其次，滤波器长度L也会产生严重的边缘效应，导致滤波后的信号比原始信号短L个采样点。该种边缘效应如图14所示。减少故障信号的长度可能会导致故障相关内容的丢失，特别是在滤波器长度L较大的情况下[21]。因此，与基于B样条插值的TEO方法相比，基于MOMEDA的方法为实际中的应用带来一些不便。

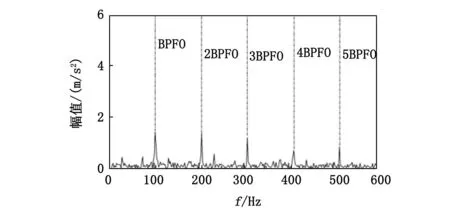
图13 滤波后信号的能量谱

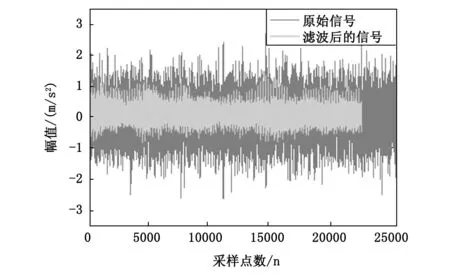
图14 原始信号和滤波信号的比较

通过对真实案例实验的结果可以发现，经典的Teager能量算子能够在存在轻微噪声的情况下检测出故障特征频率，但在恶劣的背景环境下，如存在较大噪声或故障初期，则无法提取出故障特征频率。相反，所采用的基于B样条插值的TEO在各种工况下都表现良好。虽然基于模态分解和反卷积的方法已被用于解决轴承弱故障特征的检测问题。然而，这些技术经常结合在一起，这可能导致一个复杂的过程和高计算复杂性。相比之下，该种方法显示了更直接的故障特征检测过程，这一优点使其更易于在实践中应用。

4 结论语

本文采用了一种新的能量解调算法，称为基于B样条插值的能量算子方法，用于提取电梯电机滚动轴承的故障相关特征。该种方法将信号逼近技术与经典的Teager能量算子技术相结合，大大提高了鲁棒性。该方法的显著优点是理论简单，计算效率高，应用方便和对强噪声具有较强的鲁棒性。最后，将基于模态分解和反卷积的两种常用故障检测方法与本文提出的方法进行比较。可以看到，基于B样条插值的TEO方法不管是在提取效果上还是便捷性上都明显强于EEMD和TEO结合的方法。与基于MOMEDA和TEO结合的方法相比时，不可否认这两种方法都具有较好的故障特征识别性能。然而，就便利性和实用性而言，基于B样条插值的TEO提供了更好的选择。此外，MOMEDA也会导致数据的丢失。因此，基于B样条插值的TEO方法为电梯电机轴承故障诊断提供了一种新的思路。