基于IMFAC的无人艇抗干扰航向自适应控制

包 涛，王 琦，周则兴，陈 卓

(1.中国船舶科学研究中心，江苏 无锡 214082；2.深海技术科学太湖实验室，江苏 无锡 214082)

0 引言

无人水面艇(USV，unmanned surface vessel)，也被称为无人艇，是一种能够在江河湖海等水域上进行自主航行的，可遂行预定的自主作业任务的水上平台[1-2]。目前，无人艇在海洋勘探、水下探测、海洋监测、区域巡逻、科学调查等领域发挥了越来越重要的作用。无人艇机动性高、自主性好、环境适应性强，在军事以及民用领域均有十分强大的应用潜力，因此近年来已成为全球智能海洋装备研发领域的研究焦点之一[3-4]，而其中航向控制的自适应和智能化则是无人艇实现其自主航行控制的关键。

无人艇在水域执行作业任务时，风、流、浪等水面环境经常对艇体产生扰动，同时其操纵运动模型又具有比较复杂的非线性特征，导致无人艇的艏摇等运动加剧，致使无人艇的任务载荷难以发挥作业能力，严重的甚至可能导致任务失败，因此对无人艇航向的控制方法提出了比较高的要求。目前针对无人艇航向控制算法，学术界按照是否具有被控对象信息分为基于模型的控制技术和无模型控制技术。典型的基于模型的控制技术包括：滑膜控制[6]、鲁棒控制[7]、最优控制[8]、反步控制[9]等，基于模型的控制技术其特征在于：航向控制率的构建过程中需要无人艇模型参数的参与，如反步控制方法，其是由无人艇运动数学模型反向推导设计得到航向控制率，当被控系统的模型可以被精确地数学化时，基于模型的控制方法可以达到良好的控制效果，如经典的倒立摆问题等，但是实际工程中被控系统经常具有复杂的非线性特征，同时存在大量的环境干扰，对于这些特征和干扰，常规方法难以建立准确的模型，不准确的数学模型将导致基于模型的控制方法效果下降甚至失效。常见的无模型控制技术主要包括：PID控制[10]、迭代学习控制[11]、无模型自适应控制[12]以及各种新兴的智能控制方法[13-14]。PID控制是早期流行的控制技术，其不需要被控系统的模型参数，可以仅通过系统输入输出数据的比例、微分和积分操作，实现对被控系统的镇定控制，但其控制效果较为粗略，在系统变动较大时需要重新调整控制参数；另一种无模型控制技术同样不关注被控系统模型，仅使用系统输入/输出(I/O)数据，控制率的构建中不包括被控系统的任何参数，同时该方法因为包含对系统实时在线估计，因此在被控系统的模型参数不准确、较复杂或时常变动的情况下也具有较为优秀的控制效果。

20世纪末，北京交通大学的侯忠生开发了一种被称为无模型自适应控制(MFAC，model free adaptive control)的方法[15]，方法中提出了一种区别于其他同类方法的动态线性化方法，同时提出了伪偏导数的新定义，方法在被控系统的每个动态工作点处都建立一个与之等价的动态线性化数据模型，然后基于此等价的虚拟数据模型再设计相应的控制器并进行了理论分析，从而实现非线性系统的自适应控制。MFAC方法具有以下优势：仅依赖被控系统实时量测的数据；不需要任何外在的测试信号或训练过程；方法简单、计算负担小、易于实现且鲁棒性强。

MFAC方法中的动态线性化方法有3种具体形式，分别为紧格式动态线性化(CFDL，compat form dynamic linearization)、偏格式动态线性化(PFDL，partial form dynamic linearization)和全格式动态线性化(FFDL，full form dynamic linearization)，3种方法的计算量依次上升，对被控系统的控制效果也依次上升。考虑到控制系统的实时性要求，以及本文试验对象有限的硬件条件，本文使用了偏格式动态线性化方法作为无模型自适应控制器的动态线性化方法，文章首先设计了虚拟输出量以改进算法性能，同时利用改进细菌觅食算法对IMFAC算法的参数初始值进行预整定，最后在模拟的环境干扰下进行了半物理仿真试验，同时建立了传统控制方法，并与本文的IMFAC控制方法进行了效果对比，从而对算法的有效性进行了验证。

1 考虑干扰的无人艇航向操纵运动模型

本文设计的无人艇改进无模型自适应航向控制器在实船应用中无需获取无人艇本身的模型参数信息，但是在控制器的半物理仿真测试以及最后的结果分析阶段仍需要一种能近似反映无人艇状态以及算法性能的验证模型。因此下面介绍所使用的航向响应模型和干扰模型。

在船舶航向控制中，本文使用的是野本谦作教授提出的一阶非线性响应模型[16]：

(1)

式中，r为首摇角速率；δ为舵角；T为追随性时间常数；K为舵角增益；α为Norbbin系数，其具体数值可以由螺旋实验确定；d为干扰；ψ为航向角。

为了在半物理仿真试验中模拟无人艇在航行中受到的环境扰动，需要对式(1)的干扰项d做进一步分析。无人艇所受的环境扰动一般可以分成两大类，一类是海风、海流对无人艇的扰动，另一类是海浪对无人艇的扰动。海风、海流对船舶的扰动通常在短时间内是一个恒定值，因此为了在合理范围内简化无人艇的干扰模型，使用定常值加随机白噪声的方式模拟无人艇收到的海风和流的干扰。对于海浪的干扰，根据文献[17]的描述，可以利用式(2)建立起海浪对无人艇舵角的扰动关系，从而将海浪扰动加入无人艇航向操纵运动模型中。

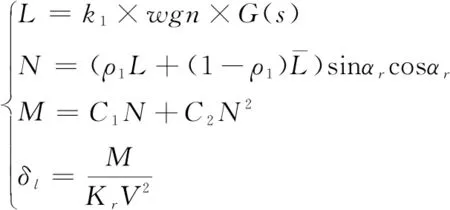
(2)

式中，L为海浪波高；k1为有色噪声比例系数；wgn为高斯白噪声；G(s)为有色噪声到波高的传递函数；N为无人艇首摇扰动力矩；αr为无人艇航向与海浪方向的夹角；C1、C2、ρ1为试验确定的系数；Kr为比例系数，与船的尺寸、吨位等有关；V为无人艇速(m/s)，δl为等效的干扰舵角。

2 无人艇抗干扰航向自适应控制器设计

2.1 PFDL-MFAC算法的改进

无模型自适应控制(MFAC)器的构建核心在于对被控非线性系统的动态线性化改写上，文献[15]中列举了针对多种被控系统的动态线性化方法，并且给出了严格的数学证明。

考虑到无人艇所受环境干扰较为复杂，且船舶动作具有一定的滞后性，以及未来可能应用的实船有限的硬件条件，本文基于偏格式动态线性化的无模型自适应(PFDL-MFAC)方法，将当前时刻的一个固定长度滑动时间窗口内的所有输入变化量的影响都考虑进来，并针对无人艇航向控制，设计了虚拟输出项以满足无模型自适应控制假设条件，建立基于偏格式动态线性化方法的无模型自适应航向控制器。

对于一般的单输入单输出非线性离散系统：

y(k+1)=f(y(k)，…，y(k-ny)，u(k)，

…，u(k-nu))

(3)

式中，u(k)∈R，y(k)∈R是系统在k时刻的输出和输入；ny，nu是未知的正整数。

当系统满足假设1及2时如下。

假设1：f(…)关于第(ny+2)个变量到第(ny+L+1)个变量分别存在连续偏导数；

假设2：系统(3)满足Lipschitz条件，即对任意k1≠k2，k1，k2≥0和UL(k1)≠UL(k2)有：

(4)

其中：y(ki+1)=f(y(ki)，…，y(ki-ny)，u(ki)，…，u(ki-nu))，i=1，2；b>0是一个常数；UL(k)=[u(k)，…，u(k-L+1)]T，L为输入线性化长度常数。

系统(3)可表示为：

(5)

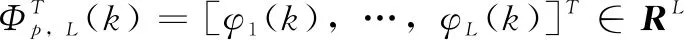
可以注意到，系统(1)的输出ψ并不能满足假设2，即当控制量递增时，受控系统的输出应当是不减的假设，因此设计系统虚拟输出项[18]：

y(k)=ψ(k)+KZr(k)

(6)

式中，KZ是设定的常数。

此时，当KZ的值合适的话，随着输入的控制量的增加，KZr(k)也会随之增加，以抵消ψ(k)下降对总输出的影响，保证被控系统符合假设2。

结合设计的系统虚拟输出项，被控系统的控制方案可设计为：

u(k)=u(k-1)+

(7)

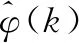
(8)

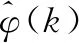
2.2 改进细菌觅食算法

在偏格式线性化的无模型自适应算法中，需要人工预先设定的参数有步长因子ρ1、ρ2、ρ3、η，权重因子λ、μ，输入线性化长度常数L共7个，其中L的大小决定了算法的复杂度，一般不超过5，其余6个参数值的选取范围较为宽大，人工选取较为费时且难以保证最优，本文使用改进的细菌觅食算法对改进无模型自适应算法的参数初值进行全局寻优，以加快改进无模型自适应算法的收敛速度，提高算法鲁棒性。

细菌觅食算法(BFO，bacterial foraging optimistic)是一种较为新颖的群体智能优化算法，算法参考了一种细菌的觅食行为中的智能特征，创造出了该生物集群算法[18]。BFO算法对控制参数的选择适应性高、算法自身具有较强抗干扰性，同时结构较为清晰简洁，并且可以实现并行处理。

图1是细菌觅食算法的基本操作流程图，算法在工作时主要通过模拟细菌的下面几种行为操作，依次是趋向性操作、聚集性操作、复制性操作和迁徙性操作。趋向性操作使“细菌”向优势位置移动；聚集性操作使“细菌”集中于多个局部最优位置；复制性操作保证优势位置的“细菌”数量增加，提高搜索效率；最后的迁徙性操作则保证了“细菌”不会陷入局部最优值。算法在进行计算时，需要优化的目标信息使用模拟细菌的位置信息表示，而目标是否符合优化需求则利用算法设置的适应度函数值的大小来测试。

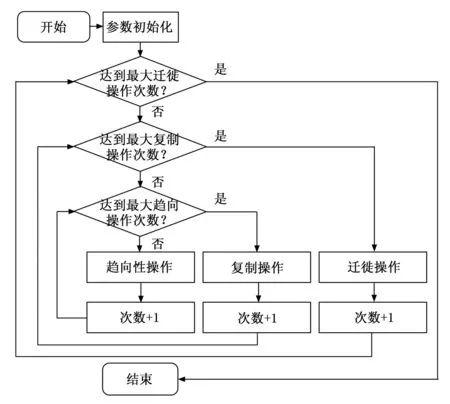
图1 细菌觅食算法基本步骤

趋向性操作的改进：

算法中的虚拟细菌在趋向操作中将会模拟真实细菌觅食时的旋转和游动的运动，具体利用数学公式描述为式(9)。

(9)

式中，θi(j，k，l)表示第i个细菌在第j次趋向操作，第k次复制操作，和第l次驱散操作时细菌所在的位置；C(i)为细菌的游动步长；Δ(i)为细菌在搜索空间内的任意方向上的一个随机向量。

图2阐述了本文对趋向操作中的游动步骤的改进后计算流程。在游动运动步骤中，原始算法中的细菌在游动后进行适应度值的判断，当适应度值的结果优于上一位置的结果时细菌将继续游动，否则细菌停止游动操作。原始算法的游动步骤会使因游动而产生适应度值下降的细菌保留低适应度值的位置，这使算法的模拟细菌在每次趋向操作后都产生了大量适应度值劣于之前的细菌个体，大大降低算法的收敛速度。为了解决这种操作漏洞，本文对游动步骤进行了改造，借助文献[20]提出的细菌智能探针，研究人员站在观察者视角，对所有进行游动步骤的细菌预计算未来位置的适应度值，当计算结果的值对比当前位置更具有优势时，细菌将保留当前游动操作指令，并向目标位置游动，反之细菌将不前进。这种改进可以保证每一个模拟细菌前进的方向都是越来越优势的位置，不会出现逆向优化的情况，同时迁徙性操作也保证了算法不会陷入局部最优值。经过测试，该方法在不改变算法计算量的前提下，大大提高了算法的收敛速度。

(10)

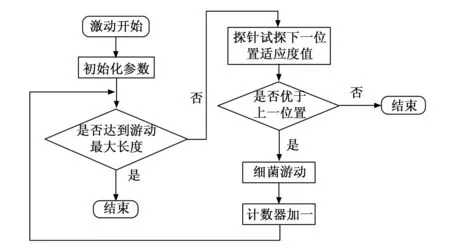
图2 改进的游动操作流程

2.3 无人艇抗干扰航向自适应控制器

结合改进细菌觅食算法和改进无模型自适应算法，本文提出了一种抗干扰的无人艇航向自适应控制器，控制器的整体结构如图3所示。

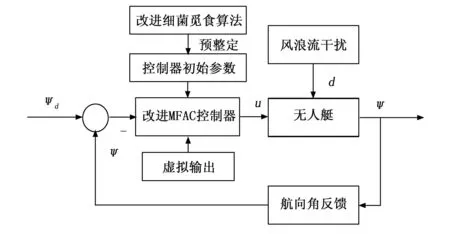
图3 无人艇抗干扰航向自适应控制器

整个无人艇抗干扰航向自适应控制器按照以下流程运行：首先，自适应控制器将接收无人艇自主导航系统提供的期望航向角与当前无人艇的实时航向角，将这些数据作为改进无模型自适应控制器(IMFAC)的数据输入，无模型自适应控制器的7个初始控制参数由改进细菌觅食算法利用与被实验船相同类型的已知船的仿真模型在虚拟仿真系统中全局寻优得到(在整个控制过程中，初始参数的寻优仅仅需要运行一次，后续控制参数将由IMFAC算法自行自适应调整，预寻优的目的是为了加快算法的收敛速度，降低人工调参工作量)，同时设计虚拟输出项以满足IMFAC控制器的假设条件2，IMFAC控制器利用控制率式(10)输出控制量即无人艇的舵角控制量，无人艇收到舵角控制指令后动作舵角执行机构，最终无人艇在风浪流干扰的环境下产生姿态和运动的变化，通过导航系统的实时测量航向角后再反馈回控制器的输入端，从而反复迭代，完成无人艇的航向控制。

控制器的完整控制方案如式(10)：

其中，λ>0，μ>0，η∈(0，2]，ρi∈(0，1]，i=1，2，…，L，ε为一个足够小的正数。

算法初始参数值利用改进细菌觅食算法得到，算法的适应度函数为：

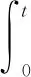
ω4ts+ω5ψover

(12)

式中，e(t)为系统偏差；Δψ(t)=ψ(t)-ψ(t-1)；ψ(t)为航向输出；ts为调整时间；ψover为绝对超调量；ω1-5为权值；Δu(t)为舵角控制量变化量。

式(12)中各项权值的大小可以影响被优化系统的各方面属性，通过调整ω1-5的大小能够使细菌觅食算法对系统调整速度、超调量、舵角调整速度等系统属性针对性优化，权值越大，代表对该项优化目标越关心，权值越小，代表对该项优化项越漠视。优秀的权值选取将能够达到对被优化系统的理想优化效果。

3 半物理仿真试验及结果分析

为了验证本文提出的IMFAC方法较传统方法更具有效性和优越性，在半物理仿真实验室中设计了有环境干扰的半物理仿真试验，试验中运动执行机构(包括双喷水推进)、无人艇控制系统(包括工控机、运动控制器、电源管理器等)均为真实设备。试验中，软件仿真系统负责模拟无人艇在水面上的运动学和动力学响应以及有干扰的环境对艇的航向控制产生的扰动；真实执行机构负责动力系统的执行和反馈；真实控制机构则负责算法的执行。半物理仿真试验能够最大程度减少实船试验的危险性和不确定性，并且可以多次重复实验，提高了算法验证效率，图4为无人艇真实物理设备图。

图4 无人艇真实物理设备图

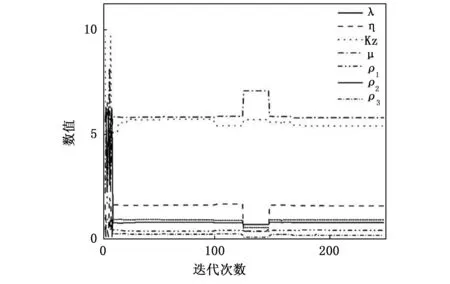
图5 IMFAC参数预整定的结果

试验中，用于验证IMFAC算法效果的无人艇操纵模型以及模拟3级海况浪干扰模型参数如表1所示。

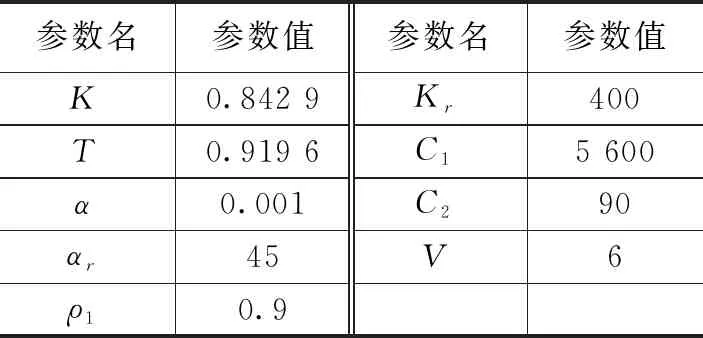
表1 无人艇操纵运动模型及干扰参数设置

在虚拟仿真系统中进行参数预整定的改进细菌觅食算法初始参数值如表2所示。

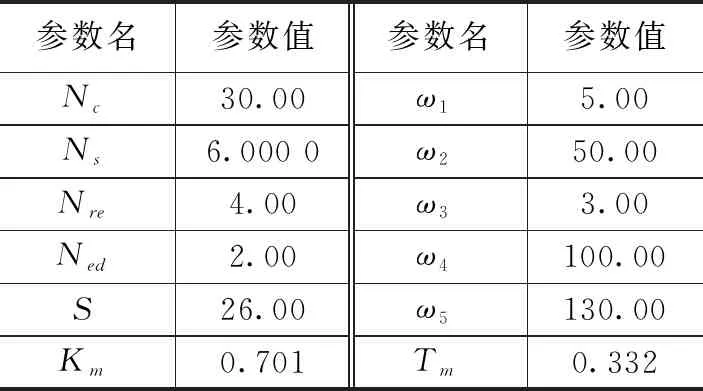
表2 BFO算法参数设置

表中，Nc为算法趋化操作次数；Ns为趋化操作运动最大步数；Nre为复制操作次数；Ned为驱散操作次数；S为细菌个数；ω1-5为适应度函数权值；Km为类似船型舵角增益；Tm为类似船型追随性时间常数。

半物理仿真试验采用以下二种航向控制工况进行验证：

1)阶跃航向控制，规定目标航向角30°，初始航向角为0°；

2)方形航向控制，每间隔30 s改变一次航向角，初始航向角为0°，阶跃梯度为30°，-30°，0°，航向的改变幅度为30°，60°，30°；

利用改进细菌觅食算法对IMFAC参数预整定的结果如图 5所示。在以上二种工况下分别与传统PID控制进行对比，二种工况下设定航向、PID航向和IMFAC航向的变化情况，以及真实航向与目标航向的误差情况的仿真结果如图 6和图 7所示。

通过改进细菌觅食算法对IMFAC的参数预整定，得出参数初始设定值：λ=0.773；η=1.573；KZ=5.376；μ=5.769；ρ1=0.413；ρ2=0.904；ρ3=0.173。经过人工手动调节寻优，PID参数调整为KP=0.8；Kd=1.2；Ki=0。

图6为无人艇30°阶跃航向控制仿真图，在模拟3级海况干扰的仿真环境下，IMFAC算法最终调整时间为10 s，稳定段最终航向误差趋于零；对比项手动优化后的PID控制的无人艇则经过约10 s达到期望值，但稳定后由于海浪、海流的干扰具有较大误差约1～2°，误差难以趋向于零。可以发现，IMFAC算法在控制速度上可以达到经过人工调参的PID算法的水平，而在干扰环境下，PID算法效果则明显不如IMFAC算法的效果，无法有效消除风浪流等环境干扰对无人艇航向控制的影响，IMFAC算法则具备将环境干扰充分抑制的效果。

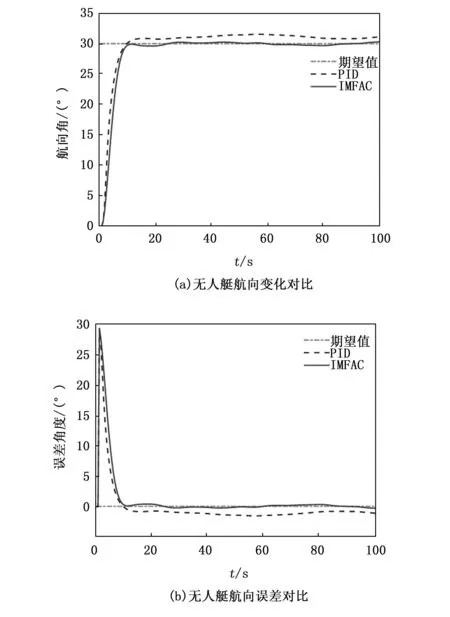
图6 无人艇30°阶跃航向控制对比

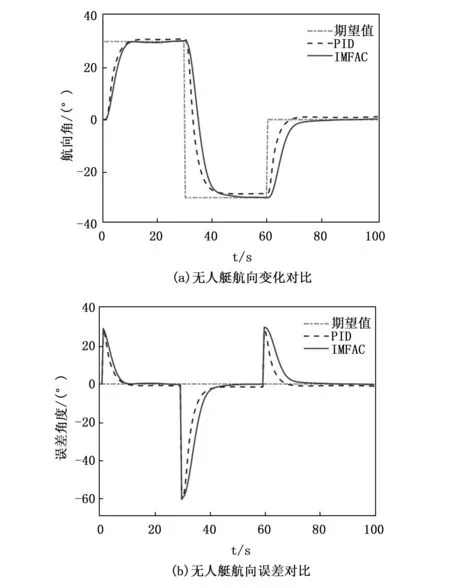
图7 无人艇方形航向控制对比

图 7为无人艇±30°方形航向控制仿真图，在模拟3级海况干扰的仿真环境下，IMFAC算法与PID算法最终调整时间均为10 s左右，对比项手动优化后的PID控制，IMFAC算法具有更小的超调量，且稳定段最终航向误差可以趋于零，PID算法则在稳定段由于海浪、海流的干扰具有更大的误差，难以趋向于零。同时还可以发现，PID算法在大范围调整航向角时，效果将变得越来越差，究其原因是PID算法人工调参时只能针对一种工况调参，无法兼顾多种情况，而IMFAC算法则没有该问题，其在线伪偏导数估计的能力保证了它可以自适应多种工况，从而在多种工况下保持其工作性能。

特别需要强调指出的是，仿真试验中PID的参数值是通过人工大量手动调参得到的最优化参数结果，调节过程费时费力，且由于干扰的存在最终控制效果较差；而本文提出的IMFAC算法的参数则可以自主获得，无需人工调参，且算法对环境干扰有明显的抑制效果，能够实现多种工况下的无人艇航向最优控制。

4 结束语

针对无人艇在航向控制中易受风浪流等环境干扰，导致控制效果下降的问题，本文提出了一种结合细菌觅食算法的改进无模型自适应控制算法，首先设计虚拟输出量改进基于偏格式动态线性化无模型自适应控制算法，同时利用改进细菌觅食算法对IMFAC算法的参数初始值进行预整定，最后在模拟的环境干扰下进行了半物理仿真试验，同时建立了传统控制方法，并与本文的IMFAC控制方法进行了效果对比，从而对算法的有效性进行了验证。本文研究结果表明：

1)改进的细菌觅食算法能够大大缩短改进无模式自适应控制算法的参数初始值的寻找时间，提高算法效果；

2)基于偏格式动态线性化(PFDL)的改进无模式自适应算法(IMFAC)具有较强的抗干扰性能和较强的收敛性，能够保证系统误差快速准确地收敛到零；

3)本文提出的无人艇抗干扰航向自适应控制器在具有一定环境干扰的情况下相较于PID算法更具优势，主要体现在本文提出的算法对于不同工况的控制效果更加稳定；在控制后期的稳定段，具有更小的跟踪误差。