二项-广义Pareto复合模型的极端海况要素推算

邱 玥,庞 亮,董 胜

(中国海洋大学工程学院,山东 青岛 266100)

引 言

海工结构物设计标准规定了根据不同重现期环境条件计算海洋环境荷载的方法。即使用长期观测或后报资料,选取合适的概率模型进行拟合,计算各种环境要素不同重现期的估计值,然后根据一定法则组合作用于海工建筑物,推求荷载。

此类研究中,以极值分布等模型为工具的概率分析是最主要的方法。常见的极值分布模型有Gumbel分布、Fréchet分布、 Weibull分布,对数正态分布、P-Ⅲ曲线等模型,也广泛的应用于极值分析[1]。以上模型采用的都是年极值取样方法,但进行极端海洋环境概率分析时关心的往往是高分位数问题。同样的置信水平,样本容量越小,得出结果的置信区间越宽,表明结果准确度低,因此样本容量的大小是影响重现期极值计算准确度的最主要因素。而许多工程海域无法保证长期、有效的实测数据,使用传统的年极值取样方式,会因信息量不足导致计算偏差。考虑到气候波候波动变化带来的不确定性影响,如果观测资料序列过短还会出现使用不同时间段的序列推求设计环境要素偏差明显的问题,即选取早期发生的样本与选取近期发生的样本得到的重现期海况计算结果会有很大的差别。解决样本不足的方法有基于阈值法取样(POT)的广义Pareto模型(GPD),刘德辅等提出的采用过程取样的复合极值分布模型[1-3]。

除了上述概率理论模型,借助数值模拟扩充样本也是解决观测数据匮乏问题的有效方法。Gatey[4]为计算50年重现期的风速,通过压力场使用Bratseth方法统计插值而得到背景风场。Dukes等[5]通过构造马尔科夫链进行数据仿真,生成了与观测值相同时间长度的序列,解决了长期观测中样本缺失的问题。研究表明当所求重现期较短时,理论方法与此方法具有相近的结果;对于超长重现期(1 000年以上),此方法得出的结果偏低。Sanabria等[6]利用蒙特卡罗法模拟生成了上千年的澳大利亚海域的风暴海况数据,并证明了他们方法的合理性。庞亮[7]、刘德辅等[8]提出的基于随机模拟与数值后报的双层嵌套概率分析模式应用于中国沿海风暴海况的长期概率分析得到了良好的效果。

为妥善解决海洋工程中因风、浪、流等多种环境要素的联合作用而产生的设计标准制定问题,多元极值模型成为发展的趋势。Gumbel等[9]最早提出了多元极值理论——对称Logistic模型,因其复杂性未能引起足够的重视。20世纪90年代,Coles等[10]详细研究了多元极值理论,提出了非对称Logistic模型、负非对称Logistic模型、Dirichlet模型,为工程界解决上述问题提供了理论依据。但多元极值模型的表达式多为隐式形式,不便于工程应用。为此,史道济等[11]提出具有更广泛应用意义的三元嵌套Logistic模型及其显式表达式。刘德辅等[1-3]提出多维复合极值分布模型。

综上所述,目前在极端海况长期概率分析领域,最需要解决的关键问题就是样本数据缺乏和不同环境要素合理组合。本文在复合极值分布理论的基础上,提出基于短期观测样本的二项-广义Pareto分布模型,并应用于极端海况要素推算。

1 理论模型构建

1.1 模型建立背景

极值理论包括BMM(Block Maximum Method)和POT(Peaks Over Threshold)两种模型。其中,BMM模型将所有的样本数据分组,选取每组最大值后,对重构的样本组进行拟合估计;POT模型则是将超过某一较大阈值所有数据作为样本,在建模过程中将超过阈值的分布近似为广义Pareto分布(GPD)[12]。已有学者对POT模型和其他数学模型在地震等巨灾事件的拟合进行了比较,均得到POT模型在拟合方面效果更佳的结论[13],且POT模型在观测值较少的情况下,估计的准确性较高[14]。在实际问题中,原始数据资料中超过阈值的样本个数有限,其取值服从二项分布,预测方法可见《概率论与数理统计》一书中的附录二所示[15]。因此,本文将POT模型筛选超阈值得到的二项分布与GPD模型得到的连续型极值分布进行组合,构造复合极值分布,即二项-广义Pareto复合分布。

1.2 模型建立过程

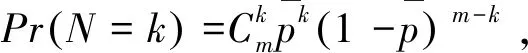
(1)

Fμ(y)为超阈量的分布函数,表示为:

(2)

对于充分大的阈值μ,超阈量Yi近似服从广义Pareto分布,即:

(3)

式中,Gξσ(u)(y)为广义Pareto分布,用于描述极端海况序列,例如风速、波高、波周期等,得其分布函数为

(4)

式中,位置参数u∈R,尺度参数σ>0,形状参数ξ∈R。

令x=y+μ,则(4)可变形为:

(5)

将上述离散型分布Y(x)与连续型极值分布Gξσ(u)(x)构造复合极值分布,即二项-广义Pareto复合分布,则其分布函数为:

由表2可知，各因素对提取辣椒碱含量影响的主次顺序为：酶解时间>酶解温度>酶添加量>料液比>SSL的添加量>粒度；各因素对提取辣椒二氢碱含量影响的主次顺序为：酶解时间>酶添加量>酶解温度>粒度>料液比>SSL的添加量，而最优水平组合为A3B1C2D1E3F2，即纤维素酶添加量0.4%(W/W)、酶解时间4 h、酶解温度45 ℃、料液比1∶8 (g/mL)、SSL的添加量1%(W/W)、辣椒粒度100目，此时，辣椒碱的含量可达7.82 mg/g，辣椒二氢碱的含量为4.94 mg/g。

(6)

代入各项,得二项-广义Pareto复合分布函数表达式为:

(7)

极端海洋工程环境的概率分析关心的是高分位数问题,希望通过计算预测出多年一遇的极端波高,提前做好防范工作,以降低自然灾害给人类带来的影响[16]。

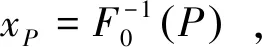
(8)

(9)

同时,我们将基于年极值波高数据,利用Gumbel极值分布、对数正态分布进行多年一遇波高值的预测,并将预测结果与上述二项-广义Pareto复合分布预测的波高值进行比较,以说明二项-广义Pareto复合分布模型更适用于巨灾事件的统计分析。其中,Gumbel极值分布和对数正态分布的设计波高计算公式如下:

Gumbel的分布函数为:

F(x)=exp{1-exp [-a(x-b)]}

(10)

(11)

对数正态分布的分布函数为:

(12)

多年一遇的设计波高为:

(13)

2 算例

2.1 阈值选取

阈值的合理选取关系到超阈值样本的样本数量和二项-广义Pareto复合分布中的参数估计,是POT模型成功拟合的关键。若阈值选取过小,超阈量分布与二项-广义Pareto复合分布相差较大,则估计量会产生有偏估计;若阈值选取过大,超阈值样本数量个数减少,则影响模型的拟合效果[17]。

本文以中国青岛某水文站1985—1989年日最大波高数据为样本,运用HILL图法选取阈值,选取原则为找到图形尾部相对稳定的线段作为起始点,则该点的横坐标对应的数据作为阈值μ。

利用MATLAB绘制Hillplot,如图1。

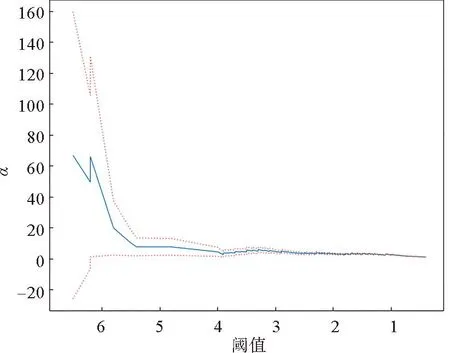
图1 Hillplot图

从图1可以看出,中尾部首次达到平稳状态时横坐标对应的值约为2.9。为了检验阈值选在2.9附近是否合理,本文结合参数稳定性估计图来进一步判断。判断方法为,在Hillplot图确定的阈值范围内,u=2.9作为初始阈值,在u=2.7到u=3.1之间均匀选取80个值作为阈值,观察计算得到的极大似然估计值在区间内是否保持相对稳定。在上述阈值的选取范围内,尺度参数和形状参数的变化趋势图如图2所示。

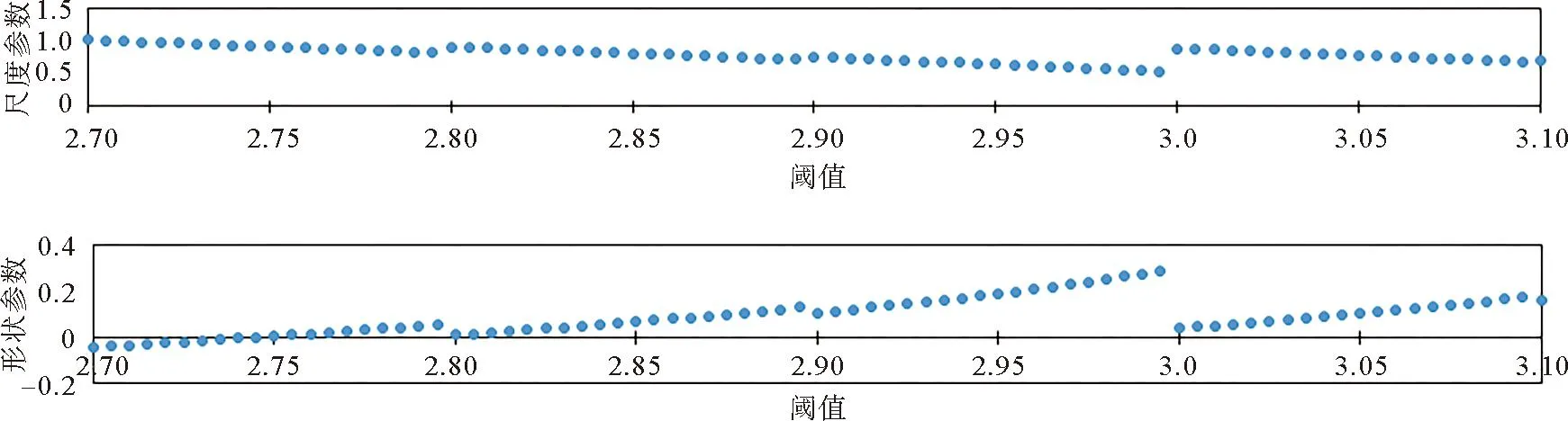
图2 不同阈值下各参数的最大似然估计值

从图2可以看出,尺度参数和形状参数均在(2.8,2.995)内保持相对稳定,为确保POT模型拟合的准确性,本文选取相对稳定区间内的较大值作为最终阈值,即u=2.995。

2.2 参数估计

在得到最佳阈值后,利用极大似然估计法对自定义的二项-广义Pareto分布函数中的各个统计参数进行估计。该复合分布的各参数见值表1。

表1 二项-广义Pareto复合分布统计参数

(14)

基于上述参数估计结果以及分布函数,为检验二项-广义Pareto分布模型是否具有较好的拟合效果,我们绘制了项-广义Pareto拟合曲线以及样本数据的经验分布曲线进行诊断。拟合曲线如图3所示。

图3 经验累积分布曲线及二项-广义Pareto拟合曲线

观察图3可以发现,参数估计结果良好,由此构造的二项-广义Pareto复合极值分布模型对日波高最大值序列具有很好的拟合效果。

为预测出多年一遇的极端波高,我们将上述各个统计参数代入式(9),得到二项-广义Pareto复合分布的分位数函数,如下:

(15)

2.3 多年一遇波高预测以及方法比较

二项-广义Pareto模型是能够使用短期观测资料推算较长重现期海况设计值的方法。而Gumbel模型、对数正态模型等是基于年极值取样的概率分析法,在计算不同重现期的设计值时都要求20～30年不等的长期海况资料,而这在很多海域无法做到。

本文利用青岛5年(1985—1989)的日最大波高数据资料,选用二项-广义Pareto模型计算多年一遇波高设计值。同时用青岛20年(1970—1989)的年极值波高数据资料,选用Gumbel模型、对数正态模型计算多年一遇波高设计值。将这三种方法所得的结果进行比较,如表2。

表2 不同分布下的不同重现期的重现水平

通过分析表2,对比50年一遇的波高重现期极值,我们可以发现自定义的二项-广义Pareto模型计算得出的结果较小,Gumbel模型、对数正态模型得到的结果近似相等。因此,我们推断基于较短样本资料,利用自定义模型计算出的50年一遇波高极值适用于设计标准低、服役年限短的海洋水工建筑物。此外,观察推求出的百年一遇、150年一遇、200年一遇的波高极值,可以发现利用自定义的二项-广义Pareto模型,采用短期数据资料预测波高值得到的结果,与采用长期数据资料,利用Gumbel模型、对数正态模型得到的结果相差不大。因此,自定义的二项-广义Pareto模型在预测波高方面是适用的。

此外可以发现,由于现有的数据很难达到完全精确和充足,导致各种复杂的统计模型也无法达到完全精确,因此没有一种模型可以在所有情况下都适用。

3 结论

本文基于POT模型,将POT模型筛选超阈值得到的二项分布与GPD模型得到的连续型极值分布进行组合,构造新的复合极值分布,即二项-广义Pareto复合分布,并应用于极端海况要素推算,得出以下主要结论:

(1)二项-广义Pareto复合分布模型具有良好的拟合效果,可以较好的描述多年一遇波高分布,弥补了传统方法需要长期原始海况数据的缺陷。

(2)运用该模型对青岛海域5年(1985—1989)的日最大波高数据进行实例分析,结果显示模型拟合较好,并分别预测了50、100、150、200年一遇的极值波高。将上述模型拟合结果与Gumbel模型、对数正态模型利用青岛海域20年(1970—1989)数据预测的50、100、150、200年一遇的极值波高结果做比较研究,结果指出:利用自定义的二项-广义Pareto模型,采用短期数据资料预测波高值得到的效果,与采用长期数据资料,利用Gumbel、对数正态模型得到的结果相差不大。得出自定义的二项-广义Pareto模型在预测波高方面是适用的。

(3)由于现有的数据很难达到完全精确,导致各种复杂的统计模型也无法达到完全精确,因此没有一种方法可以在所有情况下适用。